Как найти площадь фигуры ограниченной линиями параметрически

Когда мы выясняли геометрический смысл определенного интеграла, у нас получилась формула, с помощью которой можно найти площадь криволинейной трапеции, ограниченной осью абсцисс, прямыми x=a, x=b, а также непрерывной (неотрицательной или неположительной) функцией y=f(x). Иногда удобнее задавать функцию, ограничивающую фигуру, в параметрическом виде, т.е. выражать функциональную зависимость через параметр t. В рамках данного материала мы покажем, как можно найти площадь фигуры, если она ограничена параметрически заданной кривой.

После объяснения теории и выведения формулы мы разберем несколько характерных примеров на нахождение площади таких фигур.

Основная формула для вычисления

Допустим, что у нас имеется криволинейная трапеция, границами которой являются прямые x=a, x=b, ось Ox и параметрически заданная кривая x=φ(t)y=ψ(t), а функции x=φ(t) и y=ψ(t) являются непрерывными на интервале α; β, α<β, x=φ(t) будет непрерывно возрастать на нем и φ(α)=a, φ(β)=b.

Определение 1

Чтобы вычислить площадь трапеции при таких условиях, нужно использовать формулу S(G)=∫αβψ(t)·φ'(t)dt.

Мы вывели ее из формулы площади криволинейной трапеции S(G)=∫abf(x)dx методом подстановки x=φ(t)y=ψ(t):

S(G)=∫abf(x)dx=∫αβψ(t)d(φ(t))=∫αβψ(t)·φ'(t)dt

Определение 2

Учитывая монотонное убывание функции x=φ(t) на интервале β; α, β<α, нужная формула принимает вид S(G)=-∫βαψ(t)·φ'(t)dt.

Если функция x=φ(t) не относится к основным элементарным, то нам понадобится вспомнить основные правила возрастания и убывания функции на интервале, чтобы определить, будет ли она возрастающей или убывающей.

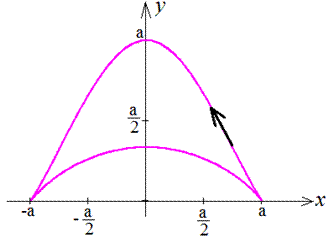
Решение задач на вычисление площади фигуры, которая ограничена параметрически заданной кривой

В этом пункте мы разберем несколько задач на применение формулы, выведенной выше.

Пример 1

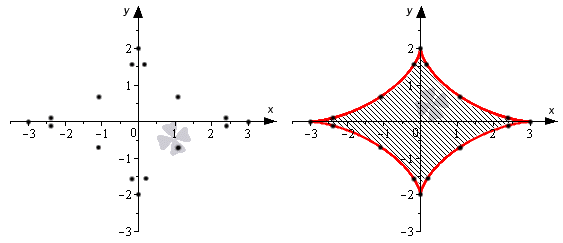
Условие: найдите площадь фигуры, которую образует линия, заданная уравнениями вида x=2cos ty=3sin t.

Решение

У нас есть параметрически заданная линия. Графически ее можно отобразить в виде эллипса с двумя полуосями 2 и 3. См на иллюстрацию:

Попробуем найти площадь 14 полученной фигуры, которая занимает первый квадрант. Область находится в интервале x∈a; b=0; 2. Далее умножим полученное значение на 4 и найдем площадь целой фигуры.

Вот ход наших вычислений:

x=φ(t)=2cos ty=ψ(t)=3sin tφα=a⇔2cos α=0⇔α=π2+πk, k∈Z,φβ=b⇔2cos β=2⇔β=2πk, k∈Z

При k, равном 0, мы получим интервал β; α=0; π2. Функция x=φ(t)=2cos t на нем будет монотонно убывать (подробнее см. статью об основных элементарных функциях и их свойствах). Значит, можно применить формулу вычисления площади и найти определенный интеграл, используя формулу Ньютона-Лейбница:

-∫0π23 sin t·2cos t’dt=6∫0π2sin2t dt=3∫0π2(1-cos(2t)dt==3·t-sin(2t)20π2=3·π2-sin2·π22-0-sin2·02=3π2

Значит, площадь фигуры, заданной исходной кривой, будет равна S(G)=4·3π2=6π.

Ответ: S(G)=6π

Уточним, что при решении задачи выше можно было взять не только четверть эллипса, но и его половину – верхнюю или нижнюю. Одна половина будет расположена на интервале x∈a; b=-2; 2. В этом случае у нас бы получилось:

φ(α)=a⇔2cos α=-2⇔α=π+πk, k∈Z,φ(β)=b⇔2cos β=2⇔β=2πk, k∈Z

Таким образом, при k равном 0, мы получили β; α=0; π. Функция x=φ(t)=2cos t на этом интервале будет монотонно убывать.

После этого вычисляем площадь половины эллипса:

-∫0π3sin t·2cos t’dt=6∫0πsin2t dt=3∫0π(1-cos(2t)dt==3·t-sin(2t)20π=3·π-sin2·π2-0-sin2·02=3π

Важно отметить, что можно взять только верхнюю или нижнюю часть, а правую или левую нельзя.

Можно составить параметрическое уравнение данного эллипса, центр которого будет расположен в начале координат. Оно будет иметь вид x=a·cos ty=b·sin t. Действуя так же, как и в примере выше, получим формулу для вычисления площади эллипса Sэлипса=πab.

Задать окружность, центр которой расположен в начале координат, можно с помощью уравнения x=R·cos ty=R·sin t, где t является параметром, а R – радиусом данной окружности. Если мы сразу воспользуемся формулой площади эллипса, то то у нас получится формула, с помощью которой можно вычислить площадь круга с радиусом R: Sкруга=πR2.

Разберем еще одну задачу.

Пример 2

Условие: найдите, чему будет равна площадь фигуры, которая ограничена параметрически заданной кривой x=3cos3ty=2sin3t.

Решение

Сразу уточним, что данная кривая имеет вид вытянутой астроиды. Обычно астроида выражается с помощью уравнения вида x=a·cos3ty=a·sin3t.

Теперь разберем подробно, как построить такую кривую. Выполним построение по отдельным точкам. Это самый распространенный метод, который применим для большинства задач. Более сложные примеры требуют проведения дифференциального исчисления, чтобы выявить параметрически заданную функцию.

У нас x=φ(t)=3cos3t, y=ψ(t)=2sin3t.

Данные функции являются определенными для всех действительных значений t. Для sin и cos известно, что они являются периодическими и их период составляет 2 пи. Вычислив значения функций x=φ(t)=3cos3t, y=ψ(t)=2sin3t для некоторых t=t0∈0; 2π π8, π4, 3π8, π2,…, 15π8, получим точки x0; y0=(φ(t0); ψ(t0)).

Составим таблицу итоговых значений:

t0	0	π8	π4	3π8	π2	5π8	3π4	7π8	π
x0=φ(t0)	3	2.36	1.06	0.16	0	-0.16	-1.06	-2.36	-3
y0=ψ(t0)	0	0.11	0.70	1.57	2	1.57	0.70	0.11	0

t0	9π8	5π4	11π8	3π2	13π8	7π4	15π8	2π
x0=φ(t0)	-2.36	-1.06	-0.16	0	0.16	1.06	2.36	3
y0=ψ(t0)	-0.11	-0.70	-1.57	-2	-1.57	-0.70	-0.11	0

После этого отметим нужные точки на плоскости и соединим их одной линией.

Теперь нам надо найти площадь той части фигуры, что находится в первой координатной четверти. Для нее x∈a; b=0; 3:

φ(α)=a⇔3cos3t=0 ⇔α=π2+πk, k∈Z,φ(β)=b⇔3cos3t=3⇔β=2πk, k∈Z

Если k равен 0, то у нас получится интервал β; α=0; π2, и функция x=φ(t)=3cos3t на нем будет монотонно убывать. Теперь берем формулу площади и считаем:

-∫0π22sin3t·3cos3t’dt=18∫0π2sin4t·cos2tdt==18∫0π2sin4t·(1-sin2t)dt=18∫0π2sin4tdt-∫0π2sin6tdt

У нас получились определенные интегралы, которые можно вычислить с помощью формулы Ньютона-Лейбница. Первообразные для этой формулы можно найти, используя рекуррентную формулу Jn(x)=-cos x·sinn-1(x)n+n-1nJn-2(x), где Jn(x)=∫sinnxdx.

∫sin4tdt=-cos t·sin3t4+34∫sin2tdt==-cos t·sin3t4+34-cos t·sin t2+12∫sin0tdt==-cos t·sin3t4-3cos t·sin t8+38t+C⇒∫0π2sin4tdt=-cos t·sin3t4-3cos t·sin t8+38t0π2=3π16∫sin6tdt=-cos t·sin5t6+56∫sin4tdt⇒∫0π2sin6tdt=-cos t·sin5t60π2+56∫0π2sin4tdt=56·3π16=15π96

Мы вычислили площадь четверти фигуры. Она равна 18∫0π2sin4tdt-∫0π2sin6tdt=183π16-15π96=9π16.

Если мы умножим это значение на 4, получим площадь всей фигуры – 9π4.

Точно таким же образом мы можем доказать, что площадь астроиды, заданной уравнениями x=a·cos3ty=a·sin3t, можно найти по формуле Sастроиды=3πa28, а площадь фигуры, которая ограничена линией x=a·cos3ty=b·sin3t, считается по формуле S=3πab8.

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Источник

Из настоящей статьи Вы научитесь находить площадь фигуры в пространстве, которая задана параметрическими кривыми.
Для этого Вам нужно знать минимум формул и хорошые знания из интегрирования.
Если имеем x=x(t), y=y(t) – параметрическое уравнение кусково-гладкой простой замкнутой кривой на промежутке [0;T], что проходит против часовой стрелки и ограничивает слева от себя фигурой то ее площадь S находим за формулой
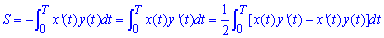Данный цикл задач в первую очередь облегчит учебу студентам мех-мату Львовского национального университета имени Ивана Франко при прохождении практикума из математического анализа.
Студенты всех Вузов могут набираться практики на подобных интегралах, и изучать методику вычисления площади.
Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький, Фединяк С.И., Филевич П.В. “Практикум из математического анализа” (рядом стоит номер из сборника Б. П. Демидовича).

Для запоминания основных моментов схема интегрирования и нахождения площадей из примера в пример будет повторяться. По возможности сами решения будут проиллюстрированы подинтегральными кривыми.

Прибор 2.100 (2413) Найти площадь фигуры, которая ограничена кривыми, заданными в параметрической форме x=a(t-sin(t)), y=a(1-cos(t)) на промежутке [0;2*Pi] и y=0.

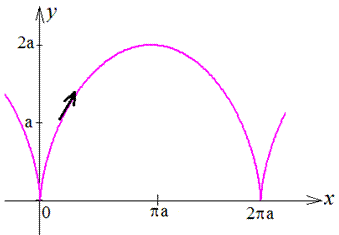
Вычисление: Циклоида – плоская трансцендентная кривая, которая определяется кинематически как траектория фиксированной точки круга радиуса a, что катится без скольжения по прямой.
Найдем производные по переменной t заданных функций:
x’=a(1-cos(t));
y’=a*sin(t).
Пределы интегрирования известны по условию – [0;2*Pi].
Запишем подинтегральную функцию за формулой x’*y-x*y’ (поскольку кривая (циклоида) проходит за ходом часовой стрелки):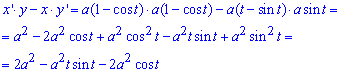
Вычислим площадь фигуры ограниченной одною аркой циклоиды:

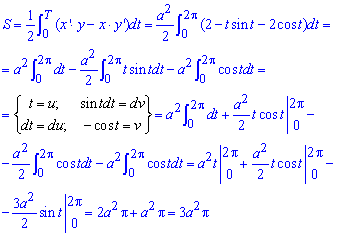
Определенные интегралы методом интегрирования частями вычисляются достаточно быстро.
Также не забывайте, что площадь измеряется в единицах квадратных.

Пример 2.101 (2414) Вычислить площадь фигуры, которая ограничена параметрическими кривыми x=2t-t², y=2t²-t³.

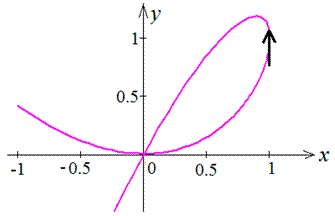
Вычисление: Вычислим производные по переменной t функций:
x’=2-2t;
y’=4t-3t².
Найдем пределы интегрирования – точки пересечения кривой, которая ограничивает заданную фигуру:
x=0 при t₁=0, t₂=2 и
y=0 при t₁=0, t₂=2 .
Поэтому имеем период ровный T=2.
Запишем подинтегральную функцию по формуле x’*y-x*y’ (поскольку кривая проходит против часовой стрелки):

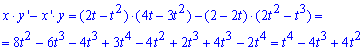
Вычислим площадь фигуры, которая ограничена заданной кривой:

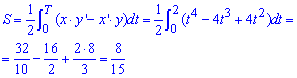
Здесь, как видите, интеграл найти вообще просто, подобные примеры на практических из математического анализа Вы возможно вычисляли огромное количество раз.

Пример 2.102 (2417.1) Найти площадь фигуры, которая ограничена параметрическими кривыми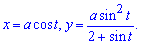

Вычисление: Продифференцируем функции по переменной t:

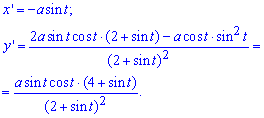
Запишем пределы интегрирования (нужно предварительно исследовать функцию):
T=[0;2*Pi].
Запишем подинтегральную функцию за формулой x’*y

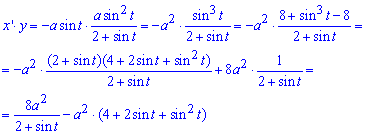
Вычислим площадь фигуры по формуле для параметрических кривых:

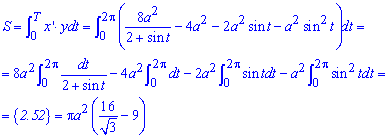
Определенный интеграл достаточно простой в плане вычислений.

Пример 2.103 (2415) Найти площадь фигуры, ограниченной кривыми
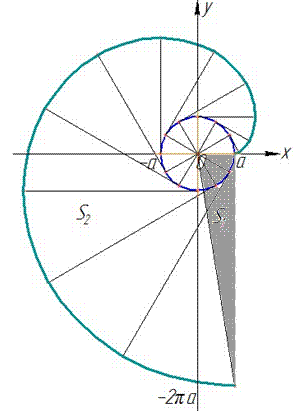
x=a(cos(t)+t*sin(t)), y=a(sin(t)-t*cos(t)) (развертка круга) и x=a, .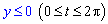

Вычисление: Найдем производные функций по переменной t:

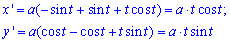
Пределы интегрирования выписываем из начального условия – [0;2*Pi].
Выведем подинтегральную функцию за формулой x’*y-x*y’

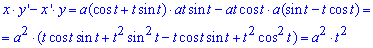
Вычислим площадь фигуры, которая ограничена заданной кривой и прямыми:

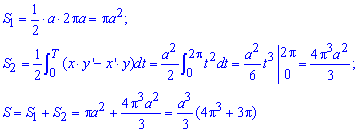
Следует заметить, что при интегрировании по углу не учитывается площадь треугольника S₁, что заштрихована серым.
Без построения графика функции учесть необходимость находить дополнительную площадь достаточно трудно.

Пример 2.104 (2416) Найти площадь фигуры, ограниченной кривыми
x=a(2*cos(t)-cos(2t)), y=a(2*sin(t)-sin(2t)).

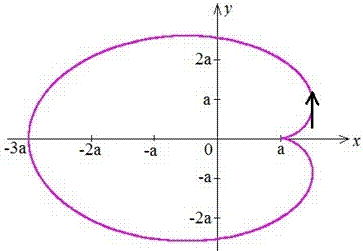
Вычисление: Вычислим производные по переменной t функций:

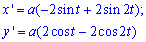
Запишем пределы интегрирования: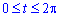
Сложим уравнение подинтегральной функции по формуле x’*y-x*y’

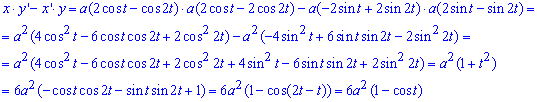
Через определенный интеграл вычисляем площадь фигуры, которая ограничена заданной кривой:

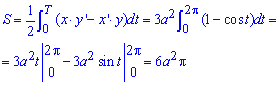
Интеграл не сложный, а конечная формула простая для расчетов площади.

Пример 2.105 (2417) Найти площадь фигуры, ограниченной параметрическими кривыми 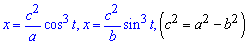(эволюта эллипса)

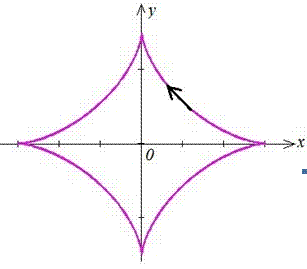
Вычисление: Эволюта – множество точек центров кривизны кривой.
По отношению к своей эволюте любая кривая является эвольвентой (інволютою, то есть разверткой этой кривой).
Найдем производные функций по переменной t :

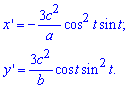
Пределы интегрирования равны:

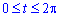
Запишем подинтегральную функцию по формуле
x’*y-x*y’:

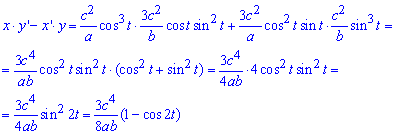
Интегрированием за периодом находим площадь фигуры, которая ограничена заданной кривой:

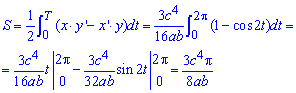
Пример 2429 Возведя уравнение к параметрическому виду, найти площади фигуры, ограниченной кривой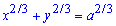 (астроида).
Вычисление: Перепишем уравнение астроиды в виде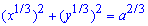

Пусть x=a*cos³(t), y=a*sin³(t).
Нетрудно подставить и убедиться, что это именно та подстановка которая будет уравнением астроиды в параметрической форме.
Далее по аналогии с примером 2.105 будем иметь

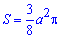
В следующих публикациях Вы найдете больше примеров на нахождение площади фигуры с помощью определенного интеграла.

Источник

Пусть кривая задана
параметрическими уравнениями
то площадь криволинейной трапеции,
ограниченной этой кривой, прямымиии отрезком [a,b]
оси ОХ, выражается формулой

,
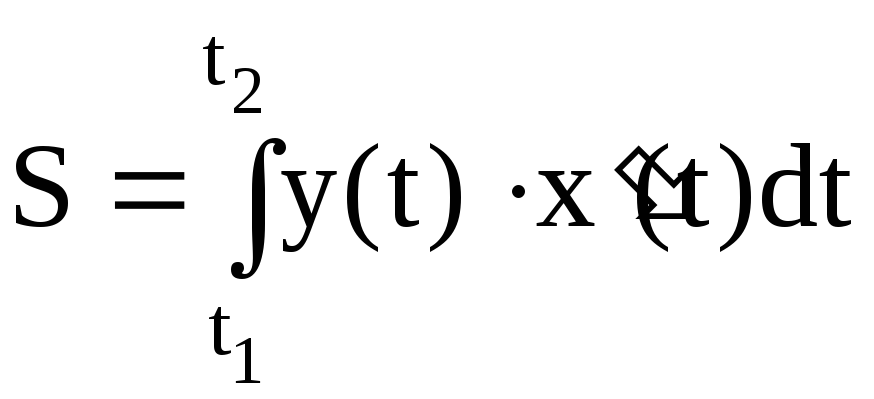(4.5)

где
,,иопределяются из условий.

Пример 45.
Найти площадь фигуры, ограниченной осью
ОХ и одной аркой циклоиды

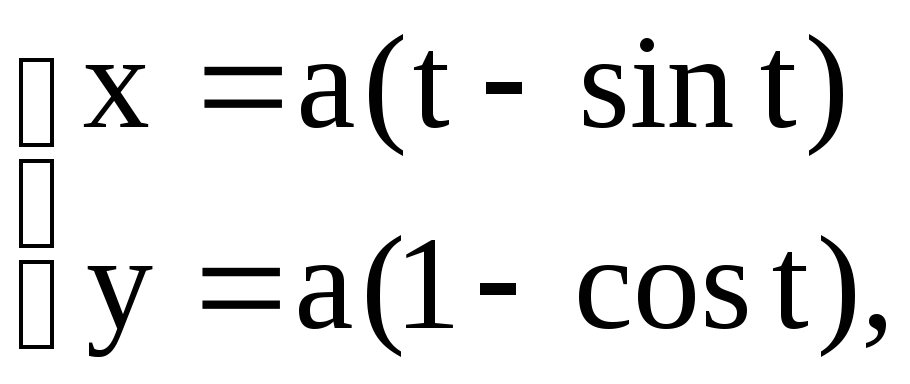
Решение.
Воспользуемся формулой (4.5). Предварительно
найдем
:

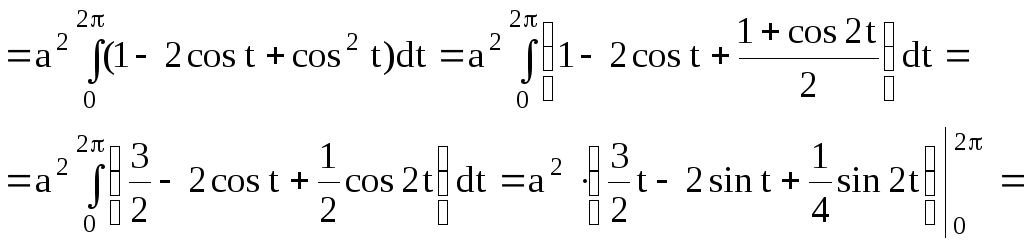
(кв.ед.)

4.3. Вычисление площади плоской фигуры в полярных координатах

В полярных
координатах положение точки на плоскости
определяется двумя координатами:
полярным радиусоми полярным углом.
Связь между декартовыми координатами
(x,y)
и полярными (,
r)
осуществляется по формулам

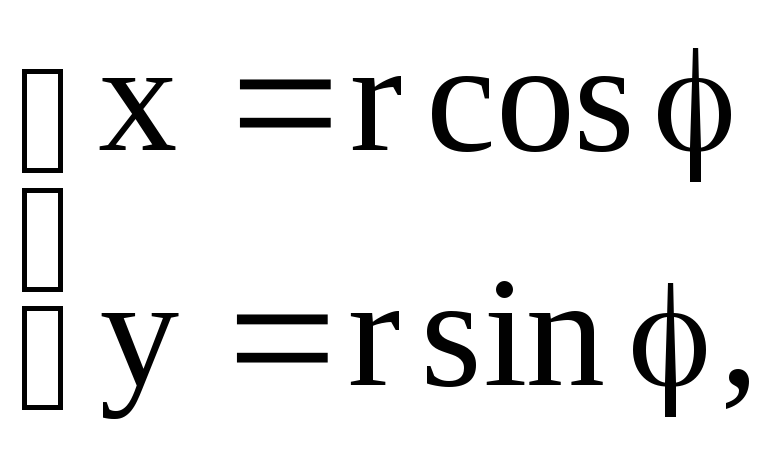
Площадь криволинейного
сектора,

ограниченного
кривой
и двумя

полярными радиусами
и

(рис.4.7), выражается
интегралом

.
(4.6)

Пример 46.
Найти площадь фигуры, ограниченной
улиткой Паскаля
.

Решение.
Воспользуемся формулой (4.6). Чтобы найти
пределы интегрирования 
и ,
необходимо построить чертеж кривой
в полярных координатах. Результаты
вычислений занесем в таблицу 1.

Таблица 1


	1		0		1
	3	2,5	2	1,5	1

Так как функция

четная, то график функции
строим симметрично относительно
горизонтальной оси для значений углов
из промежутка.
Для построения графика функции припроводим полярную осьr;
на лучах, составляющих с осью r
углы, значение которых указано в таблице
1, откладываем соответствующее расстояние,
затем точки последовательно соединяем.
Получаем замкнутую кривую, называемую
улиткой Паскаля (рис.4.8).

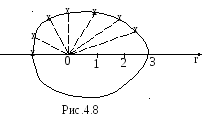
Площадь искомой
фигуры равна

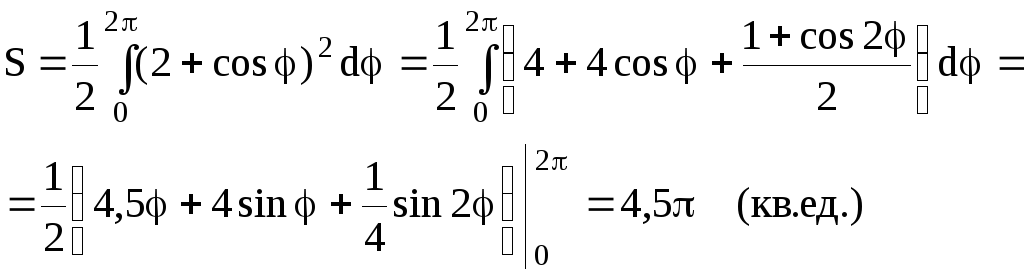
4.4. Вычисление длины дуги плоской кривой

Пусть функция f(x)
непрерывно дифференцируема на [a,b],
тогда длина дуги кривой
на указанном промежутке вычисляется
по формуле:

.
(4.7)

Если кривая гладкая
и задана параметрически, то длина дуги
этой кривой при
вычисляется по формуле:

.
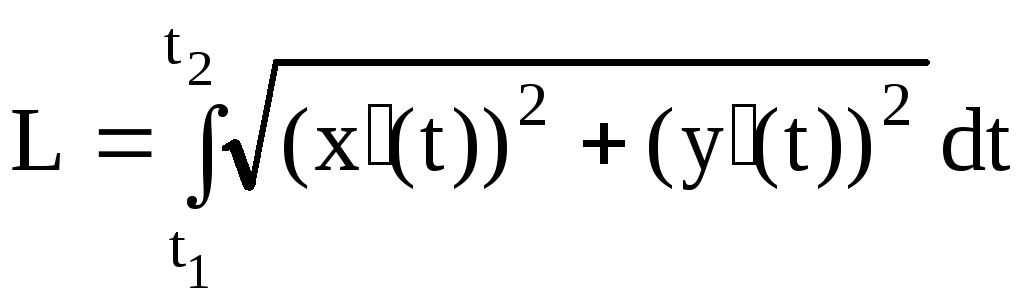(4.8)

Если гладкая кривая
задана в полярных координатах
и,
то длина ее дуги равна

.
(4.9)

Пример 47.
Вычислить длину дуги развертки окружности

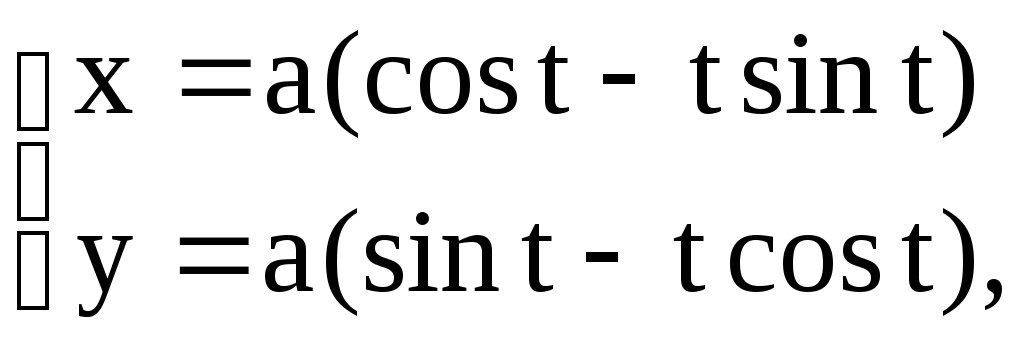
Решение.
В нашем случае кривая задана параметрически.
Воспользуемся формулой (4.8), предварительно
находим производные
и.

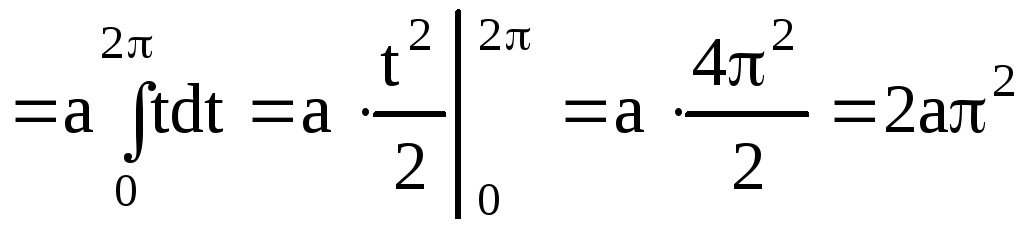(ед.длины).

Пример 48.
Найти длину дуги кривой
,.

Решение.
Кривая
задана в полярных координатах.
Воспользуемся формулой (4.9). Находим

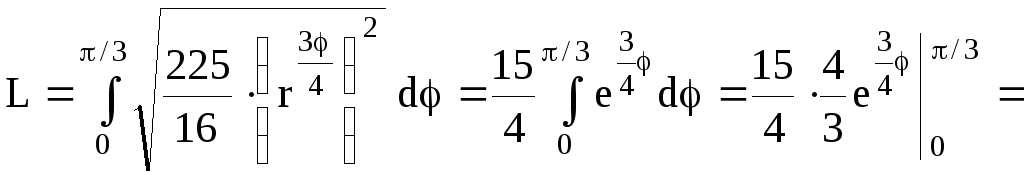
(ед.длины).

4.5. Вычисление объема тел вращения

Предположим, что
площадь сечения тела плоскостью,
перпендикулярной оси ОХ, может быть
выражена функцией от х:
при,
тогда объем тела, заключенный между
перпендикулярными оси ОХ плоскостямии,
находится по формуле

.
(4.10)

Если криволинейную
трапецию (рис.4.10) вращать вокруг оси ОХ,
то объем тела вращения будет равен

.
(4.11)

Если плоская
область, ограниченная кривыми
и прямымии,
вращается вокруг оси ОХ, то

(4.12)

Аналогично можно
записать формулы для вычисления объемов
тел вращения вокруг оси ОY:

(4.13)

(4.14)

Если кривые,
ограничивающие плоскую область заданы
в параметрическом виде, то к формулам
(4.10 – 4.14) следует применить соответствующие
замены переменной.

Если криволинейный
сектор вращать вокруг полярной оси
(см.рис.5.7), то

.
(4.15)

Пример 49.
Вычислить объем тела, полученного при
вращении дуги кривой
,вокруг оси ОХ.

Решение.
Данная кривая
называется цепной линией. График ее
изображен на рис.4.9. Объем тела вращения
(рис.4.10) вычислим по формуле (4.11)

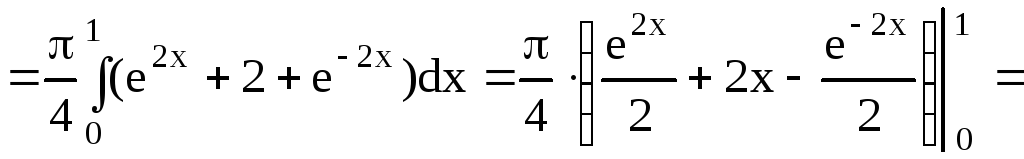
Пример 50.
Найти объем параболоида вращения, радиус
основания которого равен R,
а высота 
Н.

Решение.
Искомый параболоид вращения с указанными
параметрами получится, если будем
вращать вокруг оси ОY
параболу
,(рис.4.11; 4.12), где параметрk
легко вычислить исходя из данного
условия.

Если
,
то,
поэтому

Далее воспользуемся
формулой (4.13)

Если
то

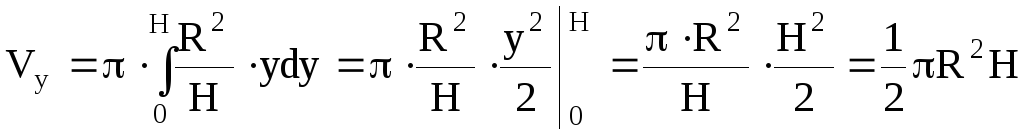(ед³).

Пример 51.
Найти объем тела вращения кривой
,вокруг
оси ОХ.

Решение.
Данная кривая задана в параметрическом
виде 

э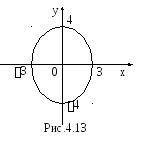то
эллипс (рис.4.13). Искомой фигурой вращения

является эллипсоид.
Найдем
по формуле (4.11)

Если
,
то,.

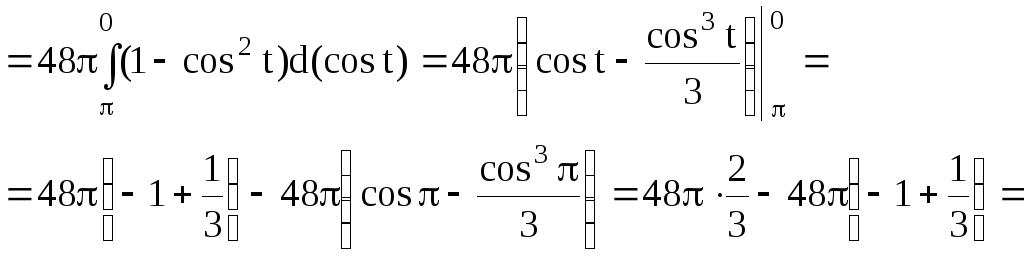
(куб.ед.).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
#
#
#
#
#
#
#
17.12.2018552.96 Кб33KA.doc
#

Источник

Вычисление площадей фигур в различных системах координат

Площадь плоской фигуры в декартовых координатах

Напомним, что мы назвали криволинейной трапецией фигуру, ограниченную осью абсцисс, прямыми x=a и x=b и графиком функции y=f(x) . В этом пункте выведем формулу для вычисления площади криволинейной трапеции.

Теорема 3. Если функция y=f(x) неотрицательна на отрезке [a;b] и непрерывна на нем, то соответствующая ей криволинейная трапеция квадрируема, причем ее площадь выражается формулой

${ S= intlimits_{a}^{b} f(x),dx,.}$

(4)

Доказательство. Криволинейная трапеция ограничена тремя отрезками и графиком непрерывной функции y=f(x) . Как было показано в пункте 2 такая фигура квадрируема. Чтобы вычислить площадь этой трапеции, построим для нее внешние и внутренние ступенчатые фигуры (см. рис. 26).

Тогда, с одной стороны, имеем:

$sum_{k=0}^{n-1}m_kDelta x_kleqslant Sleqslant sum_{k=0}^{n-1} M_kDelta x_k,,$

где $sum_{k=0}^{n-1}m_kDelta x_k$ — площадь внутренней ступенчатой фигуры, $sum_{k=0}^{n-1}M_kDelta x_k$ —площадь внешней ступенчатой фигуры, $m_k=min_{xin [x_k;x_{k+1}]}f(x)$ и $M_k=max_{xin[x_k;x_{k+1}]}f(x)$ . С другой стороны, по определению интеграла можно записать:

$sum_{k=0}^{n-1}m_kDelta x_kleqslant intlimits_{a}^{b} f(x),dxleqslant sum_{k=0}^{n-1}M_kDelta x_k,.$

Таким образом, числа и $intlimits_{a}^{b} f(x),dx$ разделяют одни и те же числовые множества: $Biggl{,sum_{k=0}^{n-1}m_kDelta x_k,Biggr},$ $Biggl{,sum_{k=0}^{n-1}M_kDelta x_k,Biggr}$ . Но, как было показано при изучении определенного интеграла, эти множества разделяются лишь одним числом, и потому $S=intlimits_{a}^{b} f(x),dx$ . Теорема доказана.

Аналогично доказывается, что если фигура ограничена снизу графиком функции y=f_1(x) , сверху графиком функции y=f_2(x) , а слева и справа прямыми x=a,~x=b (рис. 30), то ее площадь выражается формулой

$S= intlimits_{a}^{b}bigl[f_2(x)-f_1(x)bigr]dx,.$

Наглядный смысл формулы (4) состоит в том, что криволинейную трапецию можно рассматривать как объединение «бесконечно тонких полосок» с основаниями и высотами f(x) .

Площадь фигуры между двумя графиками функций

Пусть теперь функция y=f(x) непрерывна на отрезке [a;b] и принимает на нем только неположительные значения. Выразим с помощью определенного интеграла площадь соответствующей криволинейной трапеции .

Рассмотрим фигуру Phi , симметричную фигуре относительно оси . Эта фигура (рис. 31) представляет собой криволинейную трапецию, ограниченную сверху графиком непрерывной на отрезке [a;b] функции y=f(x) , которая на [a;b] принимает только неотрицательные значения. По доказанному выше

Интегрирование знакопеременной функции

$S(Phi)= intlimits_{a}^{b} bigl(-f(x)bigr)dx$ . Но S(Phi)=S(F).

Значит,

$S(F)= intlimits_{a}^{b} bigl(-f(x)bigr)dx= -intlimits_{a}^{b} f(x),dx,.$

Как мы видим, в рассматриваемом случае интеграл $intlimits_{a}^{b} f(x),dx$ дает значение площади криволинейной трапеции с точностью до знака. Если же функция меняет знак на отрезке [a;b] в конечном числе точек, то значение интеграла $intlimits_{a}^{b} f(x),dx$ дает алгебраическую сумму площадей соответствующих криволинейных трапеций, ограниченных частями графика функции y=f(x) , отрезками оси и, быть может, отрезками, параллельными оси (рис. 32).

Пример 1. Найти площадь фигуры, ограниченной кривой y=e^x , осью абсцисс и прямыми x=1,~x=2 (рис. 33).

Решение. Имеем: $S= intlimits_{1}^{2} e^x,dx= Bigl.{e^x}Bigr|_{1}^{2}= e^2-e= e(e-1)$ (кв. ед.).

Пример 2. Вычислить площадь фигуры, ограниченной дугой параболы y^2=4x и отрезком прямой x=2 (рис. 34).

Решение. Из рисунка видно, что трапеция, площадь которой нужно найти, расположена симметрично относительно оси абсцисс и, следовательно, искомая площадь равна

$S= 2int_{0}^{2}2sqrt{x},dx= left.{frac{4x^{3/2}}{3/2}}right|_{0}^{2}= frac{8}{3}cdot 2^{3/2}= frac{16}{3}sqrt{2},.$

Пример 3. Найти площадь фигуры, ограниченной графиками функций y^2=9x,~ y=3x (рис. 35).

Решение. Искомая площадь равна разности площадей криволинейного треугольника OAB и прямоугольного треугольника OAB:

$S= intlimits_{0}^{1} sqrt{9x},dx- intlimits_{0}^{1} 3x,dx= left.{3cdot frac{x^{3/2}}{3/2}}right|_{0}^{1}- left.{3cdot frac{x^2}{2} }right|_{0}^{1}= 2-frac{3}{2}= frac{1}{2},.$

Площадь фигуры, ограниченной кривой, осью абсцисс и двумя прямыми

Пример 4. Вычислить площадь фигуры, ограниченной петлей кривой a(y^2-x^2)+x^3=0 .

Решение. Из уравнения кривой видно, что она расположена симметрично относительно оси . Следовательно, можно сначала вычислить половину искомой площади (рис. 36). Рекомендуем читателю подробно исследовать и построить данную кривую.

Площадь фигуры, ограниченной петлёй кривой

Записав уравнение кривой в виде $y^2=frac{x^2}{a}(a-x)$ , найдем точки пересечения ее с осью , положив y=0colon, x_1=0,~ x_2=a . Учитывая сказанное, найдем площадь половины петли:

$frac{1}{2}S= frac{1}{sqrt{a}} intlimits_{0}^{a} xsqrt{a-x},dx,.$

Воспользовавшись формулой из таблицы при a=-1,~ b=a , получим:

$intlimits_{0}^{a} xsqrt{a-x},dx= left.{frac{2(-3x-2a)sqrt{(a-x)^3}}{15}}right|_{0}^{a}= frac{4}{15},a^{5/2},.$

Значит, окончательно имеем:

$frac{1}{2}S= frac{1}{sqrt{a}}cdot frac{4}{15},a^{5/2}= frac{4}{15},a^2quad Leftrightarrowquad S=frac{8}{15},a^2,.$

Площадь фигуры, ограниченной кривой, заданной параметрически

Пусть кривая y=f(x),~ f(x)geqslant0,~ aleqslant xleqslant b задана в параметрической форме

$begin{cases}x=varphi(t),\ y=psi(t),end{cases} alpha leqslant tleqslant b,,$

где функция x=varphi(t) монотонна на отрезке [alpha;beta] , причем varphi(alpha)=a, varphi(beta)=b , и имеет на этом отрезке непрерывную производную. Так как y=f(x)= fbigl(varphi(t)bigr)= psi(t) , то по формуле замены переменной под знаком определенного интеграла получаем:

$S= intlimits_{a}^{b} f(x),dx= intlimits_{alpha}^{beta} fbigl(varphi(t)bigr) varphi'(t),dt= intlimits_{alpha}^{beta} psi(t) varphi'(t),dt,.$

Итак, площадь фигуры, ограниченной кривой, заданной параметрически, вычисляется по формуле:

$S= intlimits_{alpha}^{beta} psi(t)varphi'(t),dt,.$

(5)

Пример 5. Вычислить площадь эллипса, заданного параметрически $begin{cases} x=acos{t},,\ y=bsin{t},,end{cases} 0leqslant tleqslant 2pi,.$

Площадь фигуры, ограниченной эллипсом

Решение. Выберем ту часть эллипса (рис. 37), которая расположена в первом квадранте. Точке A(a;0) соответствует значение t=0 , а точке B(0;b) — значение $t=frac{pi}{2}$ . Поэтому

$begin{aligned} S&= 4intlimits_{0}^{a}y,dx= -4intlimits_{0}^{pi/2}bsin{t}cdot(-asin{t}),dt= 4abintlimits_{0}^{pi/2} sin^2t,dt=\ &= 2abintlimits_{0}^{pi/2} bigl(1-cos2tbigr),dt= left.{2ab!left(t- frac{1}{2}sin2t right)}right|_{0}^{pi/2}= pi,ab,. end{aligned}$

Площадь фигуры, заданной в полярных координатах

Вычислить площадь сектора, ограниченного лучами ell и , выходящими из точки , и непрерывной кривой Gamma (рис. 38). Выберем полярную систему координат, полюсом которой является точка . Пусть rho=rho(varphi) — полярное уравнение кривой Gamma , а varphi_0 и Phi — углы между полярной осью и лучами ell и соответственно. При этом пусть функция непрерывна на [varphi_0;Phi] .

Разобьем данный сектор на частей лучами

$varphi_0< varphi_1< varphi_2< ldots< varphi_k< varphi_{k+1}< ldots< varphi_n= Phi$

и рассмотрим k-й частичный сектор $[varphi_k; varphi_{k+1}]$ (рис. 39). Пусть r_k — наименьшее значение функции rho(varphi) в $[varphi_k; varphi_{k+1}]$ , a R_k — наибольшее значение функции в этом отрезке.

Площадь в полярных координатах и разбиение сектора на n частей

Построим два круговых сектора с радиусами r_k и R_k . Обозначим через Deltavarphi_k величину угла рассматриваемого частичного сектора. Тогда площадь частичного криволинейного сектора будет заключена между площадями вписанного и описанного частичных круговых секторов

$frac{1}{2}cdot r_k^2cdot Deltavarphi_k leqslant S_kleqslant frac{1}{2}cdot R_k^2cdot Deltavarphi_k,.$

Построим аналогичным образом внутренние и внешние круговые секторы для всех частичных криволинейных секторов. Объединяя их, получим внутреннюю и внешнюю фигуры.

Площадь внутренней фигуры, состоящей из круговых секторов, равна $frac{1}{2} sum_{k=0}^{n-1} r_k^2 Deltavarphi_k$ , а площадь внешней фигуры равна — $frac{1}{2} sum_{k=0}^{n-1} R_k^2 Deltavarphi_k$ . Эти выражения являются нижней и верхней суммами Дарбу s_P и S_P для интеграла $frac{1}{2} intlimits_{varphi_0}^{Phi} rho^2(varphi),dvarphi$ . Так как функция rho(varphi) непрерывна, то непрерывна, а потому и интегрируема функция . Поэтому для любого varepsilon найдется такое разбиение отрезка [varphi_0,Phi] , что S_P-s_P<varepsilon . Из теоремы 2 пункта 2 следует, что заданный криволинейный сектор квадрируем. При этом для его площади выполняются неравенства

Площадь, ограниченная одним лепестком полярной розы

$frac{1}{2} sum_{k=0}^{n-1} r_k^2 Deltavarphi_kleqslant Sleqslant frac{1}{2} sum_{k=0}^{n-1} R_k^2 Deltavarphi_k,.$

(6)

В то же время по определению определенного интеграла

$frac{1}{2} sum_{k=0}^{n-1} r_k^2 Deltavarphi_kleqslant frac{1}{2} intlimits_{varphi_0}^{Phi} rho^2(varphi),dvarphi leqslant frac{1}{2} sum_{k=0}^{n-1} R_k^2 Deltavarphi_k,.$

(7)

В силу единственности разделяющего числа из неравенств (6) и (7) следует, что

$S= frac{1}{2} intlimits_{varphi_0}^{Phi} rho^2(varphi),dvarphi,.$

(8)

Пример 6. Вычислить площадь, ограниченную одним лепестком розы rho=asin2varphi (рис. 40).

Решение. Значениям varphi=0 и $varphi=frac{pi}{2}$ соответствует rho=0 Поэтому

$S= frac{1}{2} intlimits_{0}^{pi/2} a^2sin^22varphi,dvarphi= frac{a^2}{2} intlimits_{0}^{pi/2} frac{1-cos4varphi}{2},dvarphi= left.{frac{a^2}{4}! left(varphi- frac{1}{4}sin4varphiright)}right|_{0}^{pi/2}= frac{a^2}{4}cdot frac{pi}{2}= frac{pi}{2},a^2,.$

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Основная формула для вычисления

Решение задач на вычисление площади фигуры, которая ограничена параметрически заданной кривой

4.3. Вычисление площади плоской фигуры в полярных координатах

4.4. Вычисление длины дуги плоской кривой

4.5. Вычисление объема тел вращения

Вычисление площадей фигур в различных системах координат

Площадь плоской фигуры в декартовых координатах

Площадь фигуры, ограниченной кривой, заданной параметрически

Площадь фигуры, заданной в полярных координатах

Вам также может понравиться

Как найти все индексы символа в строке

Как найти продажу ягод грибов

Как найти человека в хмельницком на

Добавить комментарий Отменить ответ