Как найти площадь фигуры ограниченной петлей - Сайт, где вы сможете решить свои вопросы

Вычисление площадей фигур в различных системах координат

Площадь плоской фигуры в декартовых координатах

Напомним, что мы назвали криволинейной трапецией фигуру, ограниченную осью абсцисс, прямыми x=a и x=b и графиком функции y=f(x) . В этом пункте выведем формулу для вычисления площади криволинейной трапеции.

Теорема 3. Если функция y=f(x) неотрицательна на отрезке [a;b] и непрерывна на нем, то соответствующая ей криволинейная трапеция квадрируема, причем ее площадь выражается формулой

${ S= intlimits_{a}^{b} f(x),dx,.}$

(4)

Доказательство. Криволинейная трапеция ограничена тремя отрезками и графиком непрерывной функции y=f(x) . Как было показано в пункте 2 такая фигура квадрируема. Чтобы вычислить площадь этой трапеции, построим для нее внешние и внутренние ступенчатые фигуры (см. рис. 26).

Тогда, с одной стороны, имеем:

$sum_{k=0}^{n-1}m_kDelta x_kleqslant Sleqslant sum_{k=0}^{n-1} M_kDelta x_k,,$

где $sum_{k=0}^{n-1}m_kDelta x_k$ — площадь внутренней ступенчатой фигуры, $sum_{k=0}^{n-1}M_kDelta x_k$ —площадь внешней ступенчатой фигуры, $m_k=min_{xin [x_k;x_{k+1}]}f(x)$ и $M_k=max_{xin[x_k;x_{k+1}]}f(x)$ . С другой стороны, по определению интеграла можно записать:

$sum_{k=0}^{n-1}m_kDelta x_kleqslant intlimits_{a}^{b} f(x),dxleqslant sum_{k=0}^{n-1}M_kDelta x_k,.$

Таким образом, числа и $intlimits_{a}^{b} f(x),dx$ разделяют одни и те же числовые множества: $Biggl{,sum_{k=0}^{n-1}m_kDelta x_k,Biggr},$ $Biggl{,sum_{k=0}^{n-1}M_kDelta x_k,Biggr}$ . Но, как было показано при изучении определенного интеграла, эти множества разделяются лишь одним числом, и потому $S=intlimits_{a}^{b} f(x),dx$ . Теорема доказана.

Аналогично доказывается, что если фигура ограничена снизу графиком функции y=f_1(x) , сверху графиком функции y=f_2(x) , а слева и справа прямыми x=a,~x=b (рис. 30), то ее площадь выражается формулой

$S= intlimits_{a}^{b}bigl[f_2(x)-f_1(x)bigr]dx,.$

Наглядный смысл формулы (4) состоит в том, что криволинейную трапецию можно рассматривать как объединение «бесконечно тонких полосок» с основаниями и высотами f(x) .

Площадь фигуры между двумя графиками функций

Пусть теперь функция y=f(x) непрерывна на отрезке [a;b] и принимает на нем только неположительные значения. Выразим с помощью определенного интеграла площадь соответствующей криволинейной трапеции .

Рассмотрим фигуру Phi , симметричную фигуре относительно оси . Эта фигура (рис. 31) представляет собой криволинейную трапецию, ограниченную сверху графиком непрерывной на отрезке [a;b] функции y=f(x) , которая на [a;b] принимает только неотрицательные значения. По доказанному выше

Интегрирование знакопеременной функции

$S(Phi)= intlimits_{a}^{b} bigl(-f(x)bigr)dx$ . Но S(Phi)=S(F).

Значит,

$S(F)= intlimits_{a}^{b} bigl(-f(x)bigr)dx= -intlimits_{a}^{b} f(x),dx,.$

Как мы видим, в рассматриваемом случае интеграл $intlimits_{a}^{b} f(x),dx$ дает значение площади криволинейной трапеции с точностью до знака. Если же функция меняет знак на отрезке [a;b] в конечном числе точек, то значение интеграла $intlimits_{a}^{b} f(x),dx$ дает алгебраическую сумму площадей соответствующих криволинейных трапеций, ограниченных частями графика функции y=f(x) , отрезками оси и, быть может, отрезками, параллельными оси (рис. 32).

Пример 1. Найти площадь фигуры, ограниченной кривой y=e^x , осью абсцисс и прямыми x=1,~x=2 (рис. 33).

Решение. Имеем: $S= intlimits_{1}^{2} e^x,dx= Bigl.{e^x}Bigr|_{1}^{2}= e^2-e= e(e-1)$ (кв. ед.).

Пример 2. Вычислить площадь фигуры, ограниченной дугой параболы y^2=4x и отрезком прямой x=2 (рис. 34).

Решение. Из рисунка видно, что трапеция, площадь которой нужно найти, расположена симметрично относительно оси абсцисс и, следовательно, искомая площадь равна

$S= 2int_{0}^{2}2sqrt{x},dx= left.{frac{4x^{3/2}}{3/2}}right|_{0}^{2}= frac{8}{3}cdot 2^{3/2}= frac{16}{3}sqrt{2},.$

Пример 3. Найти площадь фигуры, ограниченной графиками функций y^2=9x,~ y=3x (рис. 35).

Решение. Искомая площадь равна разности площадей криволинейного треугольника OAB и прямоугольного треугольника OAB:

$S= intlimits_{0}^{1} sqrt{9x},dx- intlimits_{0}^{1} 3x,dx= left.{3cdot frac{x^{3/2}}{3/2}}right|_{0}^{1}- left.{3cdot frac{x^2}{2} }right|_{0}^{1}= 2-frac{3}{2}= frac{1}{2},.$

Площадь фигуры, ограниченной кривой, осью абсцисс и двумя прямыми

Пример 4. Вычислить площадь фигуры, ограниченной петлей кривой a(y^2-x^2)+x^3=0 .

Решение. Из уравнения кривой видно, что она расположена симметрично относительно оси . Следовательно, можно сначала вычислить половину искомой площади (рис. 36). Рекомендуем читателю подробно исследовать и построить данную кривую.

Площадь фигуры, ограниченной петлёй кривой

Записав уравнение кривой в виде $y^2=frac{x^2}{a}(a-x)$ , найдем точки пересечения ее с осью , положив y=0colon, x_1=0,~ x_2=a . Учитывая сказанное, найдем площадь половины петли:

$frac{1}{2}S= frac{1}{sqrt{a}} intlimits_{0}^{a} xsqrt{a-x},dx,.$

Воспользовавшись формулой из таблицы при a=-1,~ b=a , получим:

$intlimits_{0}^{a} xsqrt{a-x},dx= left.{frac{2(-3x-2a)sqrt{(a-x)^3}}{15}}right|_{0}^{a}= frac{4}{15},a^{5/2},.$

Значит, окончательно имеем:

$frac{1}{2}S= frac{1}{sqrt{a}}cdot frac{4}{15},a^{5/2}= frac{4}{15},a^2quad Leftrightarrowquad S=frac{8}{15},a^2,.$

Площадь фигуры, ограниченной кривой, заданной параметрически

Пусть кривая y=f(x),~ f(x)geqslant0,~ aleqslant xleqslant b задана в параметрической форме

$begin{cases}x=varphi(t),\ y=psi(t),end{cases} alpha leqslant tleqslant b,,$

где функция x=varphi(t) монотонна на отрезке [alpha;beta] , причем varphi(alpha)=a, varphi(beta)=b , и имеет на этом отрезке непрерывную производную. Так как y=f(x)= fbigl(varphi(t)bigr)= psi(t) , то по формуле замены переменной под знаком определенного интеграла получаем:

$S= intlimits_{a}^{b} f(x),dx= intlimits_{alpha}^{beta} fbigl(varphi(t)bigr) varphi'(t),dt= intlimits_{alpha}^{beta} psi(t) varphi'(t),dt,.$

Итак, площадь фигуры, ограниченной кривой, заданной параметрически, вычисляется по формуле:

$S= intlimits_{alpha}^{beta} psi(t)varphi'(t),dt,.$

(5)

Пример 5. Вычислить площадь эллипса, заданного параметрически $begin{cases} x=acos{t},,\ y=bsin{t},,end{cases} 0leqslant tleqslant 2pi,.$

Площадь фигуры, ограниченной эллипсом

Решение. Выберем ту часть эллипса (рис. 37), которая расположена в первом квадранте. Точке A(a;0) соответствует значение t=0 , а точке B(0;b) — значение $t=frac{pi}{2}$ . Поэтому

$begin{aligned} S&= 4intlimits_{0}^{a}y,dx= -4intlimits_{0}^{pi/2}bsin{t}cdot(-asin{t}),dt= 4abintlimits_{0}^{pi/2} sin^2t,dt=\ &= 2abintlimits_{0}^{pi/2} bigl(1-cos2tbigr),dt= left.{2ab!left(t- frac{1}{2}sin2t right)}right|_{0}^{pi/2}= pi,ab,. end{aligned}$

Площадь фигуры, заданной в полярных координатах

Вычислить площадь сектора, ограниченного лучами ell и , выходящими из точки , и непрерывной кривой Gamma (рис. 38). Выберем полярную систему координат, полюсом которой является точка . Пусть rho=rho(varphi) — полярное уравнение кривой Gamma , а varphi_0 и Phi — углы между полярной осью и лучами ell и соответственно. При этом пусть функция непрерывна на [varphi_0;Phi] .

Разобьем данный сектор на частей лучами

$varphi_0< varphi_1< varphi_2< ldots< varphi_k< varphi_{k+1}< ldots< varphi_n= Phi$

и рассмотрим k-й частичный сектор $[varphi_k; varphi_{k+1}]$ (рис. 39). Пусть r_k — наименьшее значение функции rho(varphi) в $[varphi_k; varphi_{k+1}]$ , a R_k — наибольшее значение функции в этом отрезке.

Площадь в полярных координатах и разбиение сектора на n частей

Построим два круговых сектора с радиусами r_k и R_k . Обозначим через Deltavarphi_k величину угла рассматриваемого частичного сектора. Тогда площадь частичного криволинейного сектора будет заключена между площадями вписанного и описанного частичных круговых секторов

$frac{1}{2}cdot r_k^2cdot Deltavarphi_k leqslant S_kleqslant frac{1}{2}cdot R_k^2cdot Deltavarphi_k,.$

Построим аналогичным образом внутренние и внешние круговые секторы для всех частичных криволинейных секторов. Объединяя их, получим внутреннюю и внешнюю фигуры.

Площадь внутренней фигуры, состоящей из круговых секторов, равна $frac{1}{2} sum_{k=0}^{n-1} r_k^2 Deltavarphi_k$ , а площадь внешней фигуры равна — $frac{1}{2} sum_{k=0}^{n-1} R_k^2 Deltavarphi_k$ . Эти выражения являются нижней и верхней суммами Дарбу s_P и S_P для интеграла $frac{1}{2} intlimits_{varphi_0}^{Phi} rho^2(varphi),dvarphi$ . Так как функция rho(varphi) непрерывна, то непрерывна, а потому и интегрируема функция . Поэтому для любого varepsilon найдется такое разбиение отрезка [varphi_0,Phi] , что S_P-s_P<varepsilon . Из теоремы 2 пункта 2 следует, что заданный криволинейный сектор квадрируем. При этом для его площади выполняются неравенства

Площадь, ограниченная одним лепестком полярной розы

$frac{1}{2} sum_{k=0}^{n-1} r_k^2 Deltavarphi_kleqslant Sleqslant frac{1}{2} sum_{k=0}^{n-1} R_k^2 Deltavarphi_k,.$

(6)

В то же время по определению определенного интеграла

$frac{1}{2} sum_{k=0}^{n-1} r_k^2 Deltavarphi_kleqslant frac{1}{2} intlimits_{varphi_0}^{Phi} rho^2(varphi),dvarphi leqslant frac{1}{2} sum_{k=0}^{n-1} R_k^2 Deltavarphi_k,.$

(7)

В силу единственности разделяющего числа из неравенств (6) и (7) следует, что

$S= frac{1}{2} intlimits_{varphi_0}^{Phi} rho^2(varphi),dvarphi,.$

(8)

Пример 6. Вычислить площадь, ограниченную одним лепестком розы rho=asin2varphi (рис. 40).

Решение. Значениям varphi=0 и $varphi=frac{pi}{2}$ соответствует rho=0 Поэтому

$S= frac{1}{2} intlimits_{0}^{pi/2} a^2sin^22varphi,dvarphi= frac{a^2}{2} intlimits_{0}^{pi/2} frac{1-cos4varphi}{2},dvarphi= left.{frac{a^2}{4}! left(varphi- frac{1}{4}sin4varphiright)}right|_{0}^{pi/2}= frac{a^2}{4}cdot frac{pi}{2}= frac{pi}{2},a^2,.$

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Вычисление площади фигуры, ограниченной кривой, заданной в параметрическом виде.

Пусть x=x(t), y=y(t),
где
–
параметрические уравнения кусочно-гладкой
кривой. Если данные уравнения определяют
некоторую функцию y=f(x)
на отрезке [a,b]
(без ограничения общности будем считать,
что
на
отрезке [a,b]),
то площадь криволинейной трапеции,
ограниченной осью OX,
кривой y=f(x)
и прямыми x=a и x=b,
может быть найдена по формуле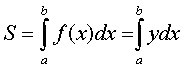
.

Вводя
замену переменной y=y(t), x=x(t), dx= x’(t)dt,
получим формулу для вычисления площади
фигуры при параметрическом задании
границы:

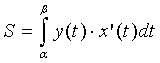
Аналогично
может быть получена формула

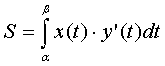
Таким
образом, вычисление площади фигуры,
ограниченной кривой в параметрической
форме, может быть рассмотрено как замена
переменной при вычислении площади в
декартовых координатах.

Если x=x(t), y=y(t),
–
параметрические уравнения кусочно-гладкой
замкнутой кривой, пробегаемой в
положительном направлении (то есть
таким образом, что фигура, ограниченная
заданным контуром остается слева), то
площадь S этой
фигуры равна:

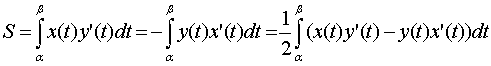
где
–
значения параметра, соответствующие
началу и концу обхода контура фигуры в
положительном направлении.

Пример
1. Найти площадь фигуры, ограниченной
кривой, заданной параметрически:
.

Решение.
Выясним, какую фигуру ограничивает
заданная кривая. Функции x=x(t)
и y=y(t)
определены, непрерывны и дифференцируемы
при любом действительном значении
параметра
.
Если
,
то
,
а если
,
то
.

Наибольшее
значение x принимает
при x’(t)=0,
2-2t=0; t=1, x(1)=1; y(1)=1.
Если x=0,
то t=2
или t=0.
При этих же значениях параметра y=0.
Таким образом, точка с координатами
(0;0) является точкой самопересечения.
Следовательно, искомая площадь ограничена
петлей кривой, расположенной в первом
квадранте, и соответствует изменению
параметра от t=0
до t=2
при положительном направлении обхода
(рисунок 7).

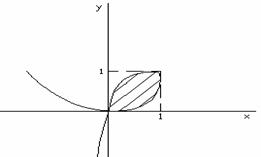
Рисунок
7.

Площадь
искомой фигуры можно вычислить по
формуле

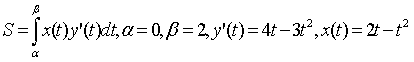
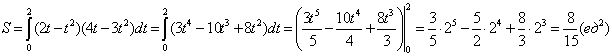
Поскольку
некоторые кривые могут быть заданы
простыми параметрическими уравнениями,
то вычисление площади фигуры, ограниченной
замкнутой кривой, в декартовых координатах
зачастую удобнее проводить, перейдя к
параметрической форме записи.

Пример
2. Вычислить площадь фигуры ограниченной
эллипсом
.

Решение.
Запишем уравнение эллипса в параметрической
форме: x=a×cost, y=b×sint,
.
Возрастание параметра от 0 до
2p соответствует
положительному направлению обхода.
Наиболее простой вид подынтегральное
выражение примет, если воспользоваться
формулой

;

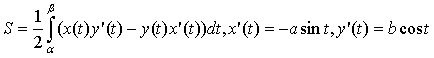
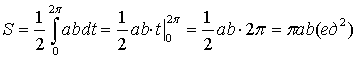
Вычисление длины дуги кривой.

Пусть
в декартовой системе координат на
плоскости дана кривая, являющаяся
графиком непрерывной дифференцируемой
функции y=f(x)
с непрерывной производной на отрезке
[a,b].
Разобьем отрезок [a,b]
произвольным образом на n частей
точками
.
Найдем значения функции f(x)
в точках разбиения. Тогда дуга кривой f(x)
на [a,b]
разобьется на n частей
точками

.
Проведем хорды
и
обозначим их длины
соответственно.
Полученная ломаная
имеет
длину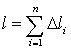
.

Определение. Длиной
дуги кривой y=f(x)
на отрезке [a,b]
называется предел, к которому стремится
длина вписанной ломаной при стремлении
к нулю длины ее наибольшего звена (или,
что то же самое, при неограниченном
увеличении числа точек деления)

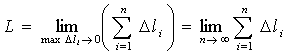
Длина
отдельного звена ломаной может быть
найдена как длина отрезка
:

Поскольку
функция f(x)
непрерывна и дифференцируема на всем
промежутке [a,b],
то, по теореме Лагранжа о дифференцируемых
функциях, найдется такая точка
на
отрезке
,
что

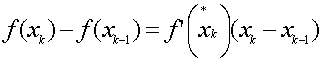
Если
обозначить
,
то формулу для
можно
переписать в виде

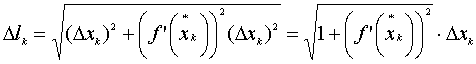
Таким
образом, длина дуги y=f(x)
на отрезке [a,b]
определяется формулой

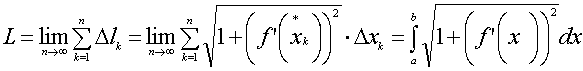
в
силу непрерывности f’(x)
и определения интегральной суммы.
Выражение
называется
дифференциалом дуги.

Если
кривая задана уравнением x=f(y), yÎ[a,b],
то, рассуждая аналогично, можно получить
формулу

,
.

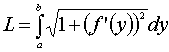
Если
кривая на плоскости задана
параметрически: x=x(t), y=y(t),
;
,
где x(t), y(t)
– дифференцируемые функции, имеющие
на отрезке
непрерывную
производную, то, выполнив замену
переменной в предыдущих формулах,
получим:

,
.

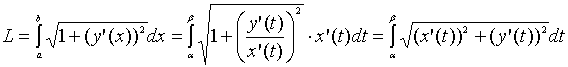
Если
задана пространственная кривая
параметрическими
уравнениями x=x(t), y=y(t), z=z(t),
,
где x(t), y(t), z(t)
– дифференцируемые на отрезке
функции
с непрерывной производной, то длина
кривой вычисляется по формуле

,
.

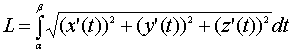
Пусть
в полярных координатах кривая задана
уравнением
,
где
–
дифференцируемая функция с непрерывной
на
производной
.
Запишем формулы перехода от декартовой
системы координат к полярной:
.
Если в эти формулы подставить
,
то получится параметрическое задание
кривой, где параметр
–
полярный угол. Тогда по формуле для
параметрически заданной функции можно
найти длину дуги кривой:

,
.

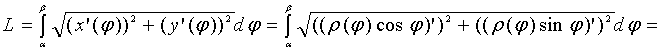
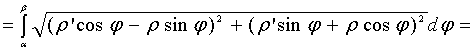
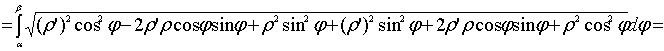
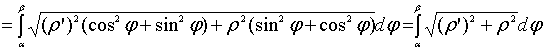
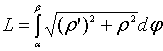
Рассмотрим
некоторые примеры вычисления длины
дуги кривой.

Пример
1. Вычислить длину дуги кривой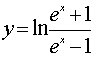
от
точки
до
точки
,
(b>a).

Решение.
Воспользуемся формулой

;

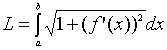
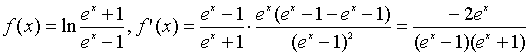
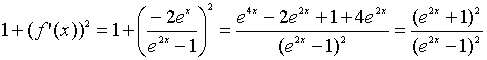
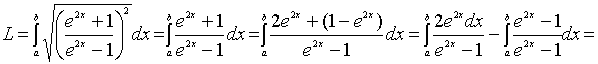
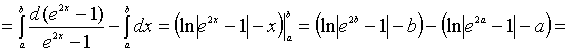
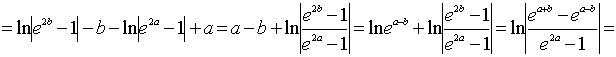
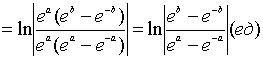
Пример
2. На циклоиде x=a(t-sint), y=a(1-cost), a>0,
найти точку, которая делит первую арку
циклоиды по длине в отношении 1:3.

Решение.
Первая арка циклоиды соответствует
изменению параметра t от t=0
до t=2p.
Вычислим длину первой арки циклоиды.

;

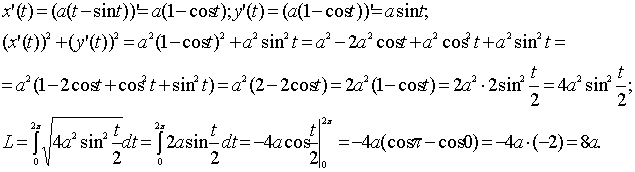
Таким
образом, искомая точка, соответствующая
значению параметра
,
определяет часть кривой, имеющую длину
2а, то есть

Найдем
из этого равенства значение
:

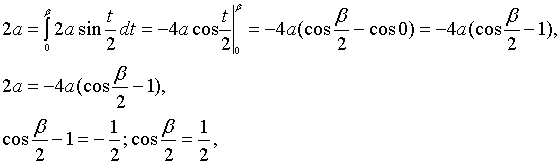
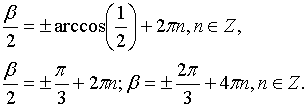
Исходя
из условий задачи, следует выбрать
значение
.

Если
,
то

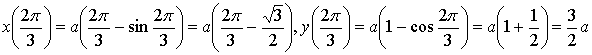
Искомая
точка имеет координаты:

Пример
3. Найти длину дуги кривой, заданной в
полярных координатах уравнением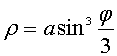
, a>0.

Решение.
Уравнение
, a>0,
определяет замкнутую кривую, соответствующую
изменению j от
0 до 3p (рисунок
8).

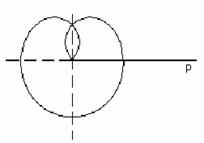
Рисунок
8.

Воспользуемся
формулой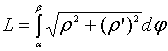
:

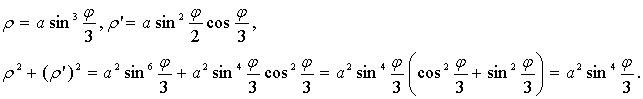
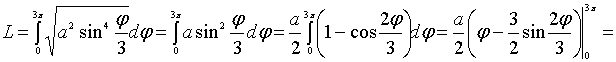
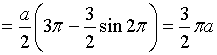
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Внимательно изучите по учебнику Г. М. Фихтенгольца главу XII, п° 193—196. Разберите примеры, приведенные в п° 196. При решении задач с геометрическим содержанием всегда старайтесь сопроводить решение чертежом.

I. Уравнения кривых заданы в декартовой системе координат.

443. Вычислить площадь фигуры, ограниченной дугой параболы, прямыми X=I9 х — А и отрезком

оси абсцисс.

Решение. В теоретическом курсе показано, что площадь криволинейной трапеции численно равна определенному интегралу

В данном случае (рис. 5) криволинейная трапеция ABDC9 площадь которой мы вычисляем, ограничена параллельными прямыми AB и CD, отрезком прямой AC и отрезком кривой линии BD.

Искомая площадь равна:

444. Вычислить площадь трапеции, ограниченной дугой параболы и отрезком прямой х = 2.

Решение. Из рисунка 6 видно, что искомая площадь расположена симметрично относительно оси абсцисс и, следовательно,

445. Вычислить площадь фигуры, ограниченной кривыми;

Решение. На рисунке 7 изображена фигура, площадь которой мы должны вычислить. Как видно из рисунка, площадь фигуры OBMAO можно представить как разность двух площадей (пл. OBMPO и OAMPU1 где MP — перпендикуляр, опущенный из точки M на ось Ох).

Найдем координаты точки Al. Решая систему уравнений

получимСледов ат ельн о,

Легко видеть, что данную задачу можно решить и другим путем. Искомую площадь можно представить в виде разности двух площадей—пл. OAMNO и пл. OBMNO (MN — перпендикуляр, опущенный из точки M на ось Oy):

Тогда

Ясно, что значение площади OBMAO не зависит от способа ее вычисления.

446. Вычислить площадь фигуры, ограниченной петлей кривой:

Решение. Из уравнений кривой видно, что она расположена симметрично относительно оси Ох. Следовательно, можно легко вычислить половину искомой площади (см. рис. 8).

Рекомендуем провести самостоятельно подробное исследование кривой.

Записав уравнение кривой в виде легко найдем точки пересечения кривой с осью Ох, положив у = 0. Мы получим.Учитывая все сказанное, окончательно найдем:

447. Вычислить площадь фигуры, ограниченной синусоидой wИ осью Ох, если

Вся площадь петли равна:

Решение. Из рисунка 9 видно, что искомая площадь на сегментеРасположена над осью Ох, а на сегменте

Под осью Ох. Следовательно, достаточно вычислить площадь, ограниченную полуволной синусоиды на отрезке|, и удвоить полученный результат:

448. Найти всю площадь фигуры, ограниченной кривыми, прямыми X = 3, X = —2 и осью Ох.

Решение. Из рисунка 10 видно, что искомая площадь может быть представлена как сумма площадей:

где BA и MN—перпендикуляры, опущенные из точек В и Al на ось Ох.

Определим координаты точек В, С, М, Р. Для этого решим следующие системы уравнений:

Решая систему (I) уравнений, найдем координаты точек В и M : В (I, 2), M {— I, 2).

Решая систему (2) уравнений, найдем координаты точки С : С (3, К».

Решая систему (3) уравнений, найдем координаты точки P : Р(— 2, 5).

Найдем теперь значения промежуточных площадей:

Отсюда

449. Найти площадь фигуры, ограниченной линиями:

450. Найти площадь фигуры, ограниченной линиями:

451. Найти площадь фигуры, ограниченной параболами:

452. Найти площадь фигуры, ограниченной линиями:

453. Найти площадь фигуры, ограниченной линиями:

454. Найти площадь «Ьигуоы. огоаниченной линиями:

455. Найти площадь круга:

456. Найти площадь эллипса

457. Найти площадь, заключенную между кривыми

458. Найти площадь фигуры, ограниченной гипоци-лоидой

459. Найти площадь фигуры, ограниченной гиперболой

И прямой

460. Вычислить площадь фигуры, заключенной между параболой, осями координат и прямой х=3,5.

461. Найти площадь фигуры, заключенной между кривыми:

462. Найти площадь частей эллипса отсеченных гиперболой

463. Найти площадь фигуры, ограниченной кривой

464. Найти площадь фигуры, заключенной между кривыми

2. Кривые заданы параметрическими уравнениями. Если кривая, ограничивающая площадь плоской фигуры, задана параметрическими уравнениями:

где функцииНепрерывны вместе со своими про

изводными наТо для вычисления площади

плоской фигуры следует в определенном интеграле произвести замену переменной:

465. Вычислить площадь, ограниченную эллипсом!

Решение. Эллипс расположен симметрично относительно обеих осей (рис. Последовательно, можно вычислить сначала• часть площади данной фигуры. Вычислим площадь той части плоской фигуры, которая расположена в первом квадранте:

Найдем пределы интегрирования для переменной t из условий:

Имеем:

466. Найти площадь фигуры, ограниченной астроидой:

PsP ш е н и е. Искомая площадь изображена на рисунке 12. Вычислим сначала площадь тсй части плоской фигуры, которая расположена в первом квадранте, это будет

Рис. 12.

часть всей искомой площади. Найдем пределы интегрирования для переменной / из условий:

Следовательно,

467. Вычислить площадь, ограниченную одной аркой циклоиды:И осью Ох.

Решение. Из рисунка 13 видно, что при изменении параметра t от 0 до 2л точка (ху у) обегает всю арку циклоиды, причем х изменяется в промежутках от 0 до 2т. Следовательно,

Вся площадь, ограниченная астроидой, равна:

468. Вычислить площадь четверти круга: x = 2cos t, y = 2sint.

469. Найти площадь, ограниченную эволютой эллипса:

(.Эволютой кривой называется геометрическое место её центров кривизны. Эволютой эллипса является деформированная астроида.)

470. Найти площадь, ограниченную кардиоидой:

х = a(2cost — cos 21), у = a (2sin/— sin 2/).

3. Кривые заданы в полярной системе координат. Из

теоретического курса известно, что площадь S1 ограниченная неподвижным полярным радиусом г0, подвижным полярным радиусом г и кривой г — /(ф), может быть вычислена по следующей формуле:

<Р> Ч, г

S = – j J/-2 Лр = J – j /(<р)]2<*Ф.

471. Вычислить площадь, ограниченную первым витком спирали Архимеда г — а<р (рис. 14).

Решение. Найдем пределы интегрирования. Первый виток спирали образуется при изменении параметра t от О до 2зх. Следовательно,

,12*

D3 Д

472. Найти площадь, ограниченную одним лепестком кривой г = a sin 2<р.

Решение. Пределы интегрирования для <р найдем из условий:

О < 2<р<я.

Отсюда

и, следовательно,

473. Вычислить площадь, ограниченную кривой г = = a cos ф.

Решение. Данная кривая—окружность радиуса у,

проходящая через полюс, расположенная симметрично относительно полярной оси. Эго легко увидеть, если перейти к декартовым координатам. (Проделайте это самостоя-

а2 I

тельно.) Тогда S = я – — = —я;а2.

7 4 4

Можно было найти искомую площадь, используя полярное уравнение данной кривой. Пределы для q> найдут* ся из условия cos ф> 0, следовательно,

S = J a® cos2 ф dq> =

TC TC

–< ф < —.

2 Y 2

Таким образом, имеем:

474. Вычислить площадь OAB (см. рис. 15), ограниченную полярными радиусамиг, = OA и r2 = OB и дугой логарифмической спирали

Решение. Будем считать, что полярному радиусу г, соответствует полярный угол фг, а полярному радиусу г2 соответствует полярный угол ф2. Тогда

475. Найти площадь петли листа Декарта:

Решение. Перейдем к полярным координатам с помощью известных соотношений:

Уравнение данной кривой в полярных координатах примет вид:

откуда

На получим

откуда

, в этом промежутке изменения полярного

углаф кривая опишет петлю. ПриИли

знаменатель стремится к нулю и, следовательно, р —» оо. Это значит, что существует асипмтота данной кривой. Найдем ее, пользуясь исходным уравнением кривой в лекап-товых координатах. Разделив обе части равенства

Из полученного уравнения кривой видно, чтоПри

и, следовательно, таким образом,

Уравнение асимптоты:

Подставляя вместо k и b найденные значения, получим искомое уравнение асимптоты данной кривой:

Для построения данной кривой совместим полюс с началом декартовых координат и будем считать положительное направление оси Ox совпадающим с направлением полярной оси. Составим таблицу значений

Соединяя теперь плавной кривой полученные точки, получим петлю данной кривой (рис. 16).

Найдем площадь, ограниченную петлей листа Декарта. Из геометрических соображений видно, что полярный угол <р

изменяется от 0 до.Tаким образом, находим:

476. Вычислить площадь круга

477. Найти площадь, ограниченную петлей лемнискаты>

Построив предварительно данную кривую.

478. Найти площадь, ограниченную кривой:

P = a cos 4<р.

479. Найти площадь, ограниченную одним лепестком кривой:

P = a cos 2ф.

480. Найти площадь фигуры, ограниченной вторым витком спирали Архимеда р = аф и отрезком полярной оси, соединяющим концы первого и второго витков (см. рис. 14).

481. Найти площадь, ограниченную улиткой Паскаля:

P = 2а (2 cos ф).

482. Вычислить площадь, ограниченную кардиоидой:

P = а (I — cos ф).

< Предыдущая		Следующая >

Источник

23.10.2022
Инструкция как оплачивать картой Каспи для Казахстана Прочитать инструкцию

22.10.2022
Для Беларуси возможно оплачивать только банковской картой выпущенной в России или через Webmoney Z.
Также для Беларуси можно оплачивать Банковской картой (“Карта Весь мир”), QIWI, ЮMoney перейдя в раздел Решения заданий (digiseller) в меню сайта

23.08.2021
ЮMoney+Банковская карта. Принимаются виды оплат: MasterCard, Visa, МИР, ЮMoney-кошелек (Снижена комиссия)
Оплата картой Каспи для Казахстана (по курсу 1руб=5,5тг), пишите на почтовый ящик pmaxim2006@mail.ru

23.08.2021
В Digiseller можно найти все решения, что и на fizmathim.ru Перейти в Магазин на Digiseller
Можно воспользоваться формой поиска по первым 3-4 словам. Способы оплаты: Банковская карта (РФ)(Visa/MasterCard/Мир) Казахстан (выбираете “Карта KZ” или “Карта RU/UA/KZ/Asia”), QIWI, ЮMoney, Webmoney, Unionpay, Alipay, Скины Steam

26.04.2019
– Все задачи оформлены в текстовом редакторе Microsoft Word, в PDF формате рассылаются решения отдельно.

– Ссылки действительны в течение 24 часов до первой попытки скачать (90 минут с момента первого скачивания).

05.02.2019
– При добавлении товаров в корзину на сумму выше 250 руб. и оформлении заказа активируется 5 % скидка на оплату.

– Ссылка на скачивание задач, приходит на указанный вами почтовый ящик при оформлении заказа и его оплаты. Дополнительная рассылка оплаченных заказов на E-mail производится в течение нескольких минут/часов, тема писем имеет вид “Заказ xxxxx”.

Источник

Привести уравнения к параметрическому виду и найти площади фигур ограниченных петлей кривой

Запрошуємо усіх хто любить цікаві задачі та головоломки відвідати групу! Зараз діє акція – підтримай студента! Знижки на роботи + безкоштовні консультації.

Контакты

Администратор, решение задач
Роман

Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym

Решение задач
Андрей

facebook:
dniprovets25

Вычисление площади фигуры, ограниченной параметрически заданной кривой

Когда мы выясняли геометрический смысл определенного интеграла, у нас получилась формула, с помощью которой можно найти площадь криволинейной трапеции, ограниченной осью абсцисс, прямыми x = a , x = b , а также непрерывной (неотрицательной или неположительной) функцией y = f ( x ) . Иногда удобнее задавать функцию, ограничивающую фигуру, в параметрическом виде, т.е. выражать функциональную зависимость через параметр t . В рамках данного материала мы покажем, как можно найти площадь фигуры, если она ограничена параметрически заданной кривой.

После объяснения теории и выведения формулы мы разберем несколько характерных примеров на нахождение площади таких фигур.

Основная формула для вычисления

Допустим, что у нас имеется криволинейная трапеция, границами которой являются прямые x = a , x = b , ось O x и параметрически заданная кривая x = φ ( t ) y = ψ ( t ) , а функции x = φ ( t ) и y = ψ ( t ) являются непрерывными на интервале α ; β , α β , x = φ ( t ) будет непрерывно возрастать на нем и φ ( α ) = a , φ ( β ) = b .

Чтобы вычислить площадь трапеции при таких условиях, нужно использовать формулу S ( G ) = ∫ α β ψ ( t ) · φ ‘ ( t ) d t .

Мы вывели ее из формулы площади криволинейной трапеции S ( G ) = ∫ a b f ( x ) d x методом подстановки x = φ ( t ) y = ψ ( t ) :

S ( G ) = ∫ a b f ( x ) d x = ∫ α β ψ ( t ) d ( φ ( t ) ) = ∫ α β ψ ( t ) · φ ‘ ( t ) d t

Учитывая монотонное убывание функции x = φ ( t ) на интервале β ; α , β α , нужная формула принимает вид S ( G ) = – ∫ β α ψ ( t ) · φ ‘ ( t ) d t .

Если функция x = φ ( t ) не относится к основным элементарным, то нам понадобится вспомнить основные правила возрастания и убывания функции на интервале, чтобы определить, будет ли она возрастающей или убывающей.

Решение задач на вычисление площади фигуры, которая ограничена параметрически заданной кривой

В этом пункте мы разберем несколько задач на применение формулы, выведенной выше.

Условие: найдите площадь фигуры, которую образует линия, заданная уравнениями вида x = 2 cos t y = 3 sin t .

Решение

У нас есть параметрически заданная линия. Графически ее можно отобразить в виде эллипса с двумя полуосями 2 и 3 . См на иллюстрацию:

Попробуем найти площадь 1 4 полученной фигуры, которая занимает первый квадрант. Область находится в интервале x ∈ a ; b = 0 ; 2 . Далее умножим полученное значение на 4 и найдем площадь целой фигуры.

Вот ход наших вычислений:

x = φ ( t ) = 2 cos t y = ψ ( t ) = 3 sin t φ α = a ⇔ 2 cos α = 0 ⇔ α = π 2 + πk , k ∈ Z , φ β = b ⇔ 2 cos β = 2 ⇔ β = 2 πk , k ∈ Z

При k , равном 0 , мы получим интервал β ; α = 0 ; π 2 . Функция x = φ ( t ) = 2 cos t на нем будет монотонно убывать (подробнее см. статью об основных элементарных функциях и их свойствах). Значит, можно применить формулу вычисления площади и найти определенный интеграл, используя формулу Ньютона-Лейбница:

– ∫ 0 π 2 3 sin t · 2 cos t ‘ d t = 6 ∫ 0 π 2 sin 2 t d t = 3 ∫ 0 π 2 ( 1 – cos ( 2 t ) d t = = 3 · t – sin ( 2 t ) 2 0 π 2 = 3 · π 2 – sin 2 · π 2 2 – 0 – sin 2 · 0 2 = 3 π 2

Значит, площадь фигуры, заданной исходной кривой, будет равна S ( G ) = 4 · 3 π 2 = 6 π .

Ответ: S ( G ) = 6 π

Уточним, что при решении задачи выше можно было взять не только четверть эллипса, но и его половину – верхнюю или нижнюю. Одна половина будет расположена на интервале x ∈ a ; b = – 2 ; 2 . В этом случае у нас бы получилось:

φ ( α ) = a ⇔ 2 cos α = – 2 ⇔ α = π + π k , k ∈ Z , φ ( β ) = b ⇔ 2 cos β = 2 ⇔ β = 2 π k , k ∈ Z

Таким образом, при k равном 0 , мы получили β ; α = 0 ; π . Функция x = φ ( t ) = 2 cos t на этом интервале будет монотонно убывать.

После этого вычисляем площадь половины эллипса:

– ∫ 0 π 3 sin t · 2 cos t ‘ d t = 6 ∫ 0 π sin 2 t d t = 3 ∫ 0 π ( 1 – cos ( 2 t ) d t = = 3 · t – sin ( 2 t ) 2 0 π = 3 · π – sin 2 · π 2 – 0 – sin 2 · 0 2 = 3 π

Важно отметить, что можно взять только верхнюю или нижнюю часть, а правую или левую нельзя.

Можно составить параметрическое уравнение данного эллипса, центр которого будет расположен в начале координат. Оно будет иметь вид x = a · cos t y = b · sin t . Действуя так же, как и в примере выше, получим формулу для вычисления площади эллипса S э л и п с а = πab .

Задать окружность, центр которой расположен в начале координат, можно с помощью уравнения x = R · cos t y = R · sin t , где t является параметром, а R – радиусом данной окружности. Если мы сразу воспользуемся формулой площади эллипса, то то у нас получится формула, с помощью которой можно вычислить площадь круга с радиусом R : S к р у г а = πR 2 .

Разберем еще одну задачу.

Условие: найдите, чему будет равна площадь фигуры, которая ограничена параметрически заданной кривой x = 3 cos 3 t y = 2 sin 3 t .

Решение

Сразу уточним, что данная кривая имеет вид вытянутой астроиды. Обычно астроида выражается с помощью уравнения вида x = a · cos 3 t y = a · sin 3 t .

Теперь разберем подробно, как построить такую кривую. Выполним построение по отдельным точкам. Это самый распространенный метод, который применим для большинства задач. Более сложные примеры требуют проведения дифференциального исчисления, чтобы выявить параметрически заданную функцию.

У нас x = φ ( t ) = 3 cos 3 t , y = ψ ( t ) = 2 sin 3 t .

Данные функции являются определенными для всех действительных значений t . Для sin и cos известно, что они являются периодическими и их период составляет 2 пи. Вычислив значения функций x = φ ( t ) = 3 cos 3 t , y = ψ ( t ) = 2 sin 3 t для некоторых t = t 0 ∈ 0 ; 2 π π 8 , π 4 , 3 π 8 , π 2 , . . . , 15 π 8 , получим точки x 0 ; y 0 = ( φ ( t 0 ) ; ψ ( t 0 ) ) .

Составим таблицу итоговых значений:

t 0	0	π 8	π 4	3 π 8	π 2	5 π 8	3 π 4	7 π 8	π
x 0 = φ ( t 0 )	3	2 . 36	1 . 06	0 . 16	0	– 0 . 16	– 1 . 06	– 2 . 36	– 3
y 0 = ψ ( t 0 )	0	0 . 11	0 . 70	1 . 57	2	1 . 57	0 . 70	0 . 11	0

t 0	9 π 8	5 π 4	11 π 8	3 π 2	13 π 8	7 π 4	15 π 8	2 π
x 0 = φ ( t 0 )	– 2 . 36	– 1 . 06	– 0 . 16	0	0 . 16	1 . 06	2 . 36	3
y 0 = ψ ( t 0 )	– 0 . 11	– 0 . 70	– 1 . 57	– 2	– 1 . 57	– 0 . 70	– 0 . 11	0

После этого отметим нужные точки на плоскости и соединим их одной линией.

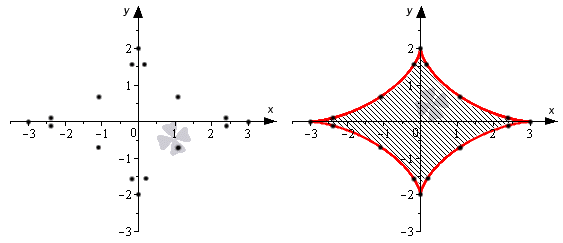
Теперь нам надо найти площадь той части фигуры, что находится в первой координатной четверти. Для нее x ∈ a ; b = 0 ; 3 :

φ ( α ) = a ⇔ 3 cos 3 t = 0 ⇔ α = π 2 + πk , k ∈ Z , φ ( β ) = b ⇔ 3 cos 3 t = 3 ⇔ β = 2 πk , k ∈ Z

Если k равен 0 , то у нас получится интервал β ; α = 0 ; π 2 , и функция x = φ ( t ) = 3 cos 3 t на нем будет монотонно убывать. Теперь берем формулу площади и считаем:

– ∫ 0 π 2 2 sin 3 t · 3 cos 3 t ‘ d t = 18 ∫ 0 π 2 sin 4 t · cos 2 t d t = = 18 ∫ 0 π 2 sin 4 t · ( 1 – sin 2 t ) d t = 18 ∫ 0 π 2 sin 4 t d t – ∫ 0 π 2 sin 6 t d t

У нас получились определенные интегралы, которые можно вычислить с помощью формулы Ньютона-Лейбница. Первообразные для этой формулы можно найти, используя рекуррентную формулу J n ( x ) = – cos x · sin n – 1 ( x ) n + n – 1 n J n – 2 ( x ) , где J n ( x ) = ∫ sin n x d x .

∫ sin 4 t d t = – cos t · sin 3 t 4 + 3 4 ∫ sin 2 t d t = = – cos t · sin 3 t 4 + 3 4 – cos t · sin t 2 + 1 2 ∫ sin 0 t d t = = – cos t · sin 3 t 4 – 3 cos t · sin t 8 + 3 8 t + C ⇒ ∫ 0 π 2 sin 4 t d t = – cos t · sin 3 t 4 – 3 cos t · sin t 8 + 3 8 t 0 π 2 = 3 π 16 ∫ sin 6 t d t = – cos t · sin 5 t 6 + 5 6 ∫ sin 4 t d t ⇒ ∫ 0 π 2 sin 6 t d t = – cos t · sin 5 t 6 0 π 2 + 5 6 ∫ 0 π 2 sin 4 t d t = 5 6 · 3 π 16 = 15 π 96

Мы вычислили площадь четверти фигуры. Она равна 18 ∫ 0 π 2 sin 4 t d t – ∫ 0 π 2 sin 6 t d t = 18 3 π 16 – 15 π 96 = 9 π 16 .

Если мы умножим это значение на 4 , получим площадь всей фигуры – 9 π 4 .

Точно таким же образом мы можем доказать, что площадь астроиды, заданной уравнениями x = a · cos 3 t y = a · sin 3 t , можно найти по формуле S а с т р о и д ы = 3 πa 2 8 , а площадь фигуры, которая ограничена линией x = a · cos 3 t y = b · sin 3 t , считается по формуле S = 3 πab 8 .

Вычисление площадей фигур в различных системах координат

Площадь плоской фигуры в декартовых координатах

Напомним, что мы назвали криволинейной трапецией фигуру, ограниченную осью абсцисс, прямыми и и графиком функции . В этом пункте выведем формулу для вычисления площади криволинейной трапеции.

Теорема 3. Если функция неотрицательна на отрезке и непрерывна на нем, то соответствующая ей криволинейная трапеция квадрируема, причем ее площадь выражается формулой

Доказательство. Криволинейная трапеция ограничена тремя отрезками и графиком непрерывной функции . Как было показано в пункте 2 такая фигура квадрируема. Чтобы вычислить площадь этой трапеции, построим для нее внешние и внутренние ступенчатые фигуры (см. рис. 26).

Тогда, с одной стороны, имеем:

где — площадь внутренней ступенчатой фигуры, —площадь внешней ступенчатой фигуры, и . С другой стороны, по определению интеграла можно записать:

Таким образом, числа и разделяют одни и те же числовые множества: . Но, как было показано при изучении определенного интеграла, эти множества разделяются лишь одним числом, и потому . Теорема доказана.

Аналогично доказывается, что если фигура ограничена снизу графиком функции , сверху графиком функции , а слева и справа прямыми (рис. 30), то ее площадь выражается формулой

Наглядный смысл формулы (4) состоит в том, что криволинейную трапецию можно рассматривать как объединение «бесконечно тонких полосок» с основаниями и высотами .

Пусть теперь функция непрерывна на отрезке и принимает на нем только неположительные значения. Выразим с помощью определенного интеграла площадь соответствующей криволинейной трапеции .

Рассмотрим фигуру , симметричную фигуре относительно оси . Эта фигура (рис. 31) представляет собой криволинейную трапецию, ограниченную сверху графиком непрерывной на отрезке функции , которая на принимает только неотрицательные значения. По доказанному выше

Как мы видим, в рассматриваемом случае интеграл дает значение площади криволинейной трапеции с точностью до знака. Если же функция меняет знак на отрезке в конечном числе точек, то значение интеграла дает алгебраическую сумму площадей соответствующих криволинейных трапеций, ограниченных частями графика функции , отрезками оси и, быть может, отрезками, параллельными оси (рис. 32).

Пример 1. Найти площадь фигуры, ограниченной кривой , осью абсцисс и прямыми (рис. 33).

Решение. Имеем: (кв. ед.).

Пример 2. Вычислить площадь фигуры, ограниченной дугой параболы и отрезком прямой (рис. 34).

Пример 3. Найти площадь фигуры, ограниченной графиками функций (рис. 35).

Решение. Искомая площадь равна разности площадей криволинейного треугольника и прямоугольного треугольника

Пример 4. Вычислить площадь фигуры, ограниченной петлей кривой .

Записав уравнение кривой в виде , найдем точки пересечения ее с осью , положив . Учитывая сказанное, найдем площадь половины петли:

Воспользовавшись формулой из таблицы при , получим:

Значит, окончательно имеем:

Площадь фигуры, ограниченной кривой, заданной параметрически

Пусть кривая задана в параметрической форме

где функция монотонна на отрезке , причем , и имеет на этом отрезке непрерывную производную. Так как , то по формуле замены переменной под знаком определенного интеграла получаем:

Итак, площадь фигуры, ограниченной кривой, заданной параметрически, вычисляется по формуле:

Пример 5. Вычислить площадь эллипса, заданного параметрически

Решение. Выберем ту часть эллипса (рис. 37), которая расположена в первом квадранте. Точке соответствует значение , а точке — значение . Поэтому

Площадь фигуры, заданной в полярных координатах

Вычислить площадь сектора, ограниченного лучами и , выходящими из точки , и непрерывной кривой (рис. 38). Выберем полярную систему координат, полюсом которой является точка . Пусть — полярное уравнение кривой , а и — углы между полярной осью и лучами и соответственно. При этом пусть функция непрерывна на .

Разобьем данный сектор на частей лучами

и рассмотрим k-й частичный сектор (рис. 39). Пусть — наименьшее значение функции в , a — наибольшее значение функции в этом отрезке.

Построим два круговых сектора с радиусами и . Обозначим через величину угла рассматриваемого частичного сектора. Тогда площадь частичного криволинейного сектора будет заключена между площадями вписанного и описанного частичных круговых секторов

Площадь внутренней фигуры, состоящей из круговых секторов, равна , а площадь внешней фигуры равна — . Эти выражения являются нижней и верхней суммами Дарбу и для интеграла . Так как функция непрерывна, то непрерывна, а потому и интегрируема функция . Поэтому для любого найдется такое разбиение отрезка , что . Из теоремы 2 пункта 2 следует, что заданный криволинейный сектор квадрируем. При этом для его площади выполняются неравенства

В то же время по определению определенного интеграла

В силу единственности разделяющего числа из неравенств (6) и (7) следует, что

Пример 6. Вычислить площадь, ограниченную одним лепестком розы (рис. 40).

[spoiler title=”источники:”]

http://zaochnik.com/spravochnik/matematika/integraly-integrirovanie/vychislenie-ploschadi-figury-ogranichennoj-paramet/

http://mathhelpplanet.com/static.php?p=ploshchadi-figur-v-razlichnykh-sistemakh-koordinat

[/spoiler]

Источник

Вычисление площадей фигур в различных системах координат

Площадь плоской фигуры в декартовых координатах

Площадь фигуры, ограниченной кривой, заданной параметрически

Площадь фигуры, заданной в полярных координатах

Вычисление площади фигуры, ограниченной кривой, заданной в параметрическом виде.

Вычисление длины дуги кривой.

Привести уравнения к параметрическому виду и найти площади фигур ограниченных петлей кривой

Контакты

Вычисление площади фигуры, ограниченной параметрически заданной кривой

Основная формула для вычисления

Решение задач на вычисление площади фигуры, которая ограничена параметрически заданной кривой

Вычисление площадей фигур в различных системах координат

Площадь плоской фигуры в декартовых координатах

Площадь фигуры, ограниченной кривой, заданной параметрически

Площадь фигуры, заданной в полярных координатах

Вам также может понравиться

Как найти девушек для фото

Как найти индийские сериалы на русском озвучке

Как найти начало в скотче

Добавить комментарий Отменить ответ