1.3. Как найти площадь плоской фигуры
с помощью двойного интеграла?
Двойной интеграл ![]() численно
численно
равен площади плоской фигуры ![]() (области интегрирования). Сначала рассмотрим задачу в общем
(области интегрирования). Сначала рассмотрим задачу в общем
виде.
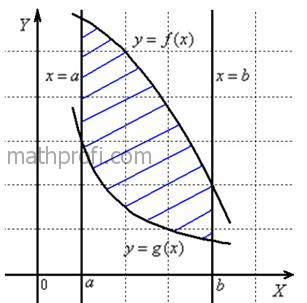
А именно вычислим площадь фигуры ![]() , ограниченной линиями
, ограниченной линиями ![]() . Для определённости считаем, что
. Для определённости считаем, что ![]() на отрезке
на отрезке ![]() .
.
Площадь заштрихованной фигуры численно равна ![]() , и сейчас мы «раскрутим» тему.
, и сейчас мы «раскрутим» тему.
Выберем первый способ обхода области:
![]()
Таким образом: 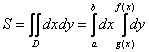
И сразу важный технический приём: повторные интегралы можно считать по отдельности. Сначала внутренний
интеграл, затем – внешний интеграл. Данный способ настоятельно рекомендую «чайникам», да и не только им. Потому что это
удобно.
1) Вычислим внутренний интеграл, при этом интегрирование проводится по переменной «игрек»:
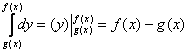
Неопределённый интеграл тут простейший, и далее используется банальная формула Ньютона-Лейбница, с той лишь
разницей, что пределами интегрирования являются не числа, а функции. Сначала подставили в «игрек» (первообразную
функцию) верхний предел, затем – нижний предел
2) Результат первого пункта нужно подставить во внешний интеграл:
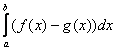
Более компактная запись всего решения выглядит так:
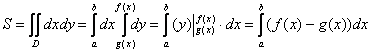
Полученная формула 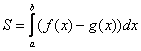 – это в
– это в
точности рабочая формула для вычисления площади плоской
фигуры с помощью обычного определённого интеграла!
То есть, задача вычисления площади с помощью двойного интеграла мало чем отличается от задачи нахождения площади с
помощью определённого интеграла!
Пример 9
С помощью двойного интеграла, вычислить площадь фигуры ![]() , ограниченной линиями
, ограниченной линиями ![]() ,
, ![]()
Решение: изобразим область ![]() на чертеже:
на чертеже:
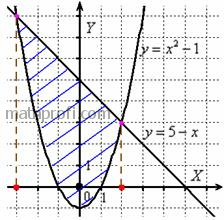
Площадь фигуры вычислим с помощью двойного интеграла по формуле:
![]()
Выберем следующий порядок обхода области (1-й способ):
![]()
Здесь и далее я не буду останавливаться на том, как выполнять обход, т.к. выше были приведены очень подробные
разъяснения.
Таким образом:
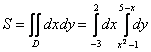
Как уже отмечалось, начинающим лучше вычислять повторные интегралы по отдельности, этого же метода буду
придерживаться и я:
1) Сначала разбираемся с внутренним интегралом:
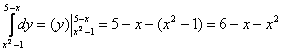
Здесь мы ВМЕСТО «игрек» сначала подставили верхний предел интегрирования ![]() , а затем – нижний:
, а затем – нижний: ![]() . Если вы запамятовали формулу Ньютона-Лейбница, обязательно
. Если вы запамятовали формулу Ньютона-Лейбница, обязательно
найдите её в приложениях! На всякий случай я приложил к данному курсу Справку по интегралам и
Справку по производным.
2) Результат, полученный на первом шаге, подставляем во внешний интеграл:
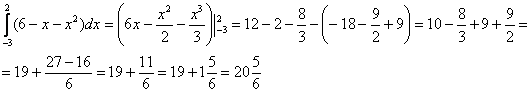
Пункт 2 – это фактически нахождение площади плоской фигуры с
помощью определённого интеграла. Обо всех тонкостях решения этой задачи (а их немало) можно ознакомиться по ссылке
выше либо в курсе Определённые и несобственные интегралы.
Это китайское напоминание.
Ответ: ![]()
Несмотря на то, что эту задачу мы неоднократно решали ранее, здесь ещё есть о чём поговорить.
Любопытное задание для самостоятельного решения:
Пример 10
С помощью двойного интеграла вычислить площадь фигуры, ограниченной линиями ![]() ,
, ![]() ,
, ![]()
Примерный образец чистового оформления задачи в конце книги.
В двух предыдущих примерах значительно выгоднее использовать первый способ
обхода области, любознательные читатели, кстати, могут изменить порядок обхода и вычислить площади вторым способом. Если
не допустите ошибку, то, естественно, получатся те же самые значения площадей.
Но в ряде случаев более эффективен второй способ обхода области, и в
заключение курса молодого «ботана» рассмотрим ещё пару примеров на эту тему:
Пример 11
С помощью двойного интеграла, вычислить площадь плоской фигуры ![]() , ограниченной линиями
, ограниченной линиями ![]() ,
, ![]()
Решение: нас с нетерпением ждут две параболы, которые «лежат на боку». Улыбаться не нужно, похожие вещи в
кратных интегралах встречаются частенько.
Представим параболу ![]() в
в
виде двух функций:
![]() – верхняя ветвь и
– верхняя ветвь и ![]() – нижняя ветвь.
– нижняя ветвь.
Аналогично, представим параболу ![]() в виде верхней
в виде верхней ![]() и нижней
и нижней ![]() ветвей.
ветвей.
Графики строим поточечно, причём, по причине симметрии, вычислений у нас в два раза меньше. В результате получается вот
такая причудливая фигура:
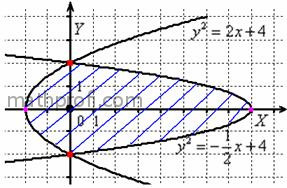
Площадь фигуры вычислим с помощью двойного интеграла по формуле:
![]()
Что будет, если мы выберем первый способ обхода области? Во-первых,
данную область придётся разделить на две части. А во-вторых, мы будем наблюдать сию печальную картину: 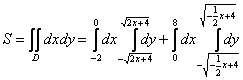 (следим по чертежу!!!). Интегралы, конечно,
(следим по чертежу!!!). Интегралы, конечно,
не «убийственные», но… есть старая математическая присказка: кто с корнями дружен, тому зачёт не нужен.
Поэтому из недоразумения, которое дано в условии, выразим обратные функции:
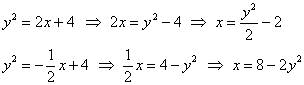
Обратные функции в данном примере обладают тем преимуществом, что задают сразу всю параболу целиком без
всяких там веток, корней и прочего дерева.
И, согласно второму способу, обход области будет следующим:
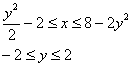
Таким образом:
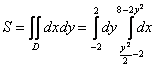
Как говорится, ощутите разницу.
1) Расправляемся с внутренним интегралом:
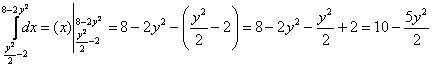
Результат подставляем во внешний интеграл:
2) 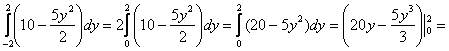
![]()
Интегрирование по переменной «игрек» не должно смущать, была бы буква «зю» – замечательно бы проинтегрировалось и по ней.
Также обратите внимание на первый шаг: подынтегральная функция ![]() является чётной, а отрезок интегрирования симметричен относительно
является чётной, а отрезок интегрирования симметричен относительно
нуля. Поэтому отрезок можно споловинить, а результат – удвоить. Что добавить…. Всё!
Ответ: ![]()
Для проверки своей техники интегрирования можете попробовать вычислить 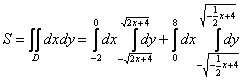 . Ответ должен получиться точно таким же.
. Ответ должен получиться точно таким же.
Пример 12
С помощью двойного интеграла, вычислить площадь плоской фигуры, ограниченной линиями ![]()
Это пример для самостоятельного решения. Интересно отметить, что если вы попробуете использовать первый способ обхода
области, то фигуру придётся разделить уже не на две, а на три части! И, соответственно, получится три пары повторных
интегралов. Бывает и такое.
Итак, начальный мастер-класс подошёл к завершению, и пора переходить на гроссмейстерский уровень. Обязательно с хорошим
настроением! – оранжевым настроением – прямо как сейчас у меня, а почему оно такое, я объясню чуть позже:
 1.4. Как вычислить произвольный двойной интеграл?
1.4. Как вычислить произвольный двойной интеграл?
 1.2.1. Как изменить порядок обхода области?
1.2.1. Как изменить порядок обхода области?
| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Разберем готовые ответы к примерам на нахождение площади плоской фигуры, которая ограничена кривыми через двойные интегралы.
Задание не сложные, а вся схема нахождения площади требует всего трех вещей:
знание элементарных функций и умение искать точки их пересечения;
понимание как через криволинейные интегралы искать площадь, умение правильно расставлять пределы;
хорошых знаний теории вычисления интегралов, поскольку к этому все сводится.
ЗАДАНИЕ 4.1 Найти площадь плоской фигуры, которая образована линиями:
x=4-y2, x+2y=4.
Решение: Фигура ограничена x=4-y2 – параболой с вершиной в точке O(4;0) и ветками влево;
но x+2y=4 – прямой, которая отрезается на осях в точках (4;0) и (0;2).
Найдем точки пересечения графиков функций из системы уравнений:
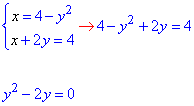
При ее решении получим две точки
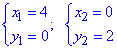
График параболы и прямой приведен на рисунку
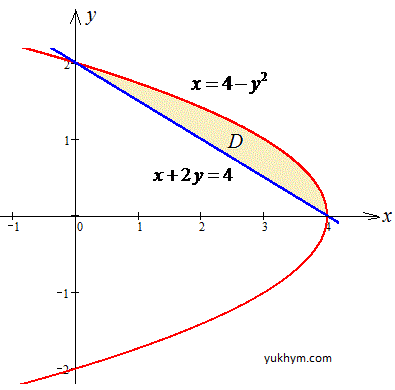
Запишем пределы интегрирования:
D: 0≤x≤4, 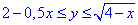
Здесь имеем y=√(4-x) – уравнение верхней части параболы x=4-y^2;
Вычислим площадь фигуры нахождением двойного интеграла:
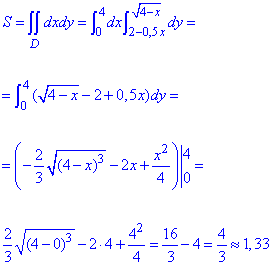
Площадь равна 1,33 единиц квадратных.
ЗАДАНИЕ 4.2 Найти площадь плоской фигуры, которая образована кривыми:
y=2-x, y2=4x+4.
Решение: y^2=4x+4 – парабола с вершиной в точке O (-1;0) и ветками вправо;
y=2-x, x+y=2 – прямая, которая отрезается на осях в точках (2;0) и (0;2).
Складываем систему уравнений для нахождения точек пересечения графиков заданных кривых:
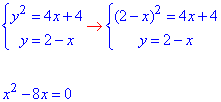
При решении получим две точки
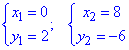
График области интегрирования имеет вид
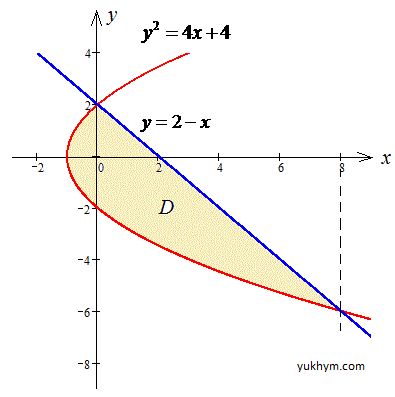
Пределы в области D:
-6≤x≤2, 0,25y2-1≤y≤2-y.
Находим площадь фигуры через криволинейный интеграл:
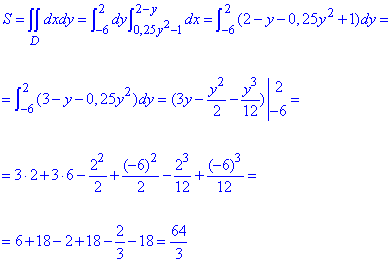
Кратный интеграл не трудно интегрировать.
ЗАДАНИЕ 4.3 Найти площадь плоской фигуры, которая образована линиями:
x2+y2=4, x2+y2=4x.
Решение: Область интегрирования ограничена x2+y2=4 – кругом с центром в точке O1(0;0) и радиусом R=2;
x2+y2=4x, x2-4x+4+y2=4, (x-2)2+y2=22 – круг с центром в точке O1(2;0) и радиусом R=2.
Найдем точки пересечения графиков заданных функций из системы уравнений:
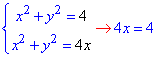
отсюда
График фигуры, площадь которой ищем приведен на рисунку
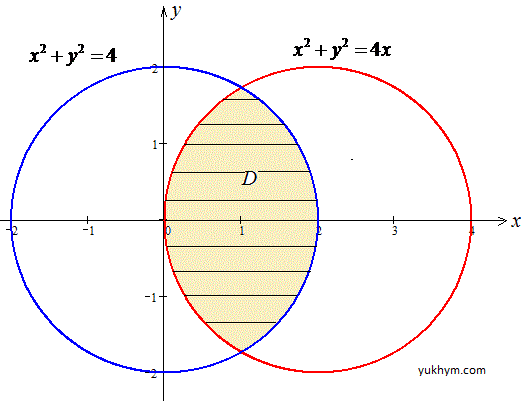
Расставим пределы в области D
(поскольку область симметрична относительно прямой y=0, то будем рассматривать ее половину, а результат умножим на 2):
D: 0≤y≤√3, 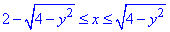
Здесь записали:
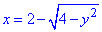 – уравнение левого полукруга (x-2)2+y2=4;
– уравнение левого полукруга (x-2)2+y2=4;
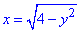 – уравнение правого полукруга x2+y2=4.
– уравнение правого полукруга x2+y2=4.
Вычислим площадь фигуры через двойной интеграл:
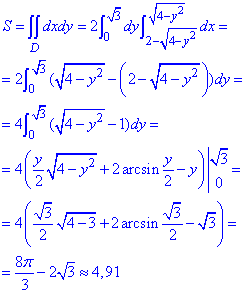
При интегрировании получили арксинусы, дальше подставили пределы интегрирования и округлили конечные значения.
ЗАДАНИЕ 4.4 Найти площадь плоской фигуры, которая образована кривыми:
x2+y2=2x, x2+y2=4x, y=x, y=0.
Решение: Начнем вычисление с анализа того, что собой представляет фигура, площадь которой нужно найти.
Сведем уравнения к простому виду
x2+y2=2x, x2-2x+1 +y2=1, (x-1)2+y2=12 – круг с центром в точке O1(1;0) и радиусом R=1.
x2+y2=4x, x2-4x+4+y2=4, (x-2)2+y2=22 – круг с центром в точке O1(2;0) и радиусом R=2.
y=x – прямая, которая является биссектрисой первой и третьей четверти.
Рисунок к задаче илюстрирует площадь которой фигуры нужно найти
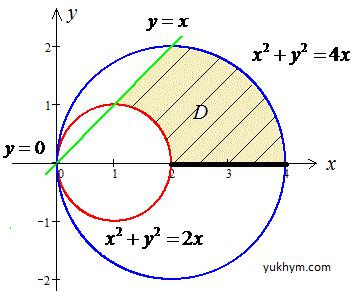
Поскольку поверхность ограничена кругами, то целесообразно перейти к полярным координатам.
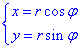
Найдем якобиан перехода:
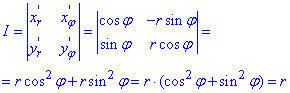
Запишем заданные функции в полярной системе координат:
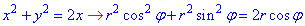
отсюда 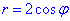
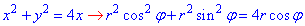
отсюда 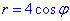
y=0, тогда 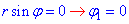
y=x, тогда 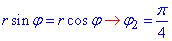
Это нам нужно, чтобы знать пределы в новой системе координат.
Пределы интегрирования в полярной системе координат:
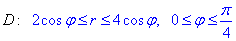
Вычислением кратного интеграла находим площадь фигуры, ограниченной заданными кривыми:
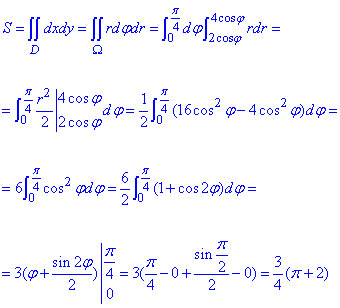
Конечное значение площади можно еще округлить.
Из этого примера Вы ознакомились как искать площадь в полярной системе координат.
В следующей статье разберем еще несколько примеров на нахождение площади фигур интегрированием.
а) Объём.
Как мы знаем, объем
V
тела, ограниченного поверхностью
![]() ,
,
где
![]() –
–
неотрицательная функция, плоскостью![]() и цилиндрической поверхностью,
и цилиндрической поверхностью,
направляющей для которой служит
граница областиD,
а образующие параллельны оси Oz,
равен двойному интегралу от функции
![]() по областиD
по областиD
:
![]()
Пример 1. Вычислить
объем тела, ограниченного поверхностями
x=0,
у=0, х+у+z=1,
z=0
(рис. 17).


Рис.17
Рис.18
Решение.
![]() D
D
– заштрихованная на рис. 17 треугольная
область в плоскости Оху,
ограниченная прямыми x=0,
у=0, x+y=1.
Расставляя пределы в двойном интеграле,
вычислим объем:
![]()
Итак,
![]() куб. единиц.
куб. единиц.
Замечание 1.
Если тело, объем которого ищется,
ограничено сверху поверхностью
![]() а снизу—поверхностью
а снизу—поверхностью![]() ,
,
причем проекцией обеих поверхностей
на плоскостьОху
является область D,
то объем V
этого тела равен разности объемов двух
«цилиндрических» тел; первое из этих
цилиндрических тел имеет нижним
основанием область D,
а верхним – поверхность
![]() второе тело имеет нижним основанием
второе тело имеет нижним основанием
также областьD,
а верхним – поверхность
![]() (рис.18).
(рис.18).
Поэтому объём V
равен разности двух двойных интегралов
:
![]()
или
![]() (1)
(1)
Легко, далее,
доказать, что формула (1) верна не только
в том случае, когда
![]() и
и![]() неотрицательны, но и тогда, когда
неотрицательны, но и тогда, когда![]() и
и![]() –
–
любые непрерывные функции, удовлетворяющие
соотношению
![]()
Замечание 2.
Если в области D
функция
![]() меняет
меняет
знак, то разбиваем область на две части:
1) областьD1
где
![]() 2) областьD2
2) областьD2
,где
![]() .
.
Предположим, что областиD1
и D2
таковы, что двойные интегралы по этим
областям существуют. Тогда интеграл
по области D1
будет положителен и будет равен
объему тела, лежащего выше плоскости
Оху. Интеграл
по D2
будет отрицателен и по абсолютной
величине равен объему тела, лежащего
ниже плоскости Оху,
Следовательно, интеграл по D
будет выражать разность соответствующих
объемов.
б) Вычисление
площади плоской области.
Если мы составим
интегральную сумму для функции
![]() по областиD,
по областиD,
то эта сумма будет равна площади S,
![]()
при любом способе
разбиения. Переходя к пределу в правой
части равенства, получим
![]()
Если область D
правильная , то площадь выразится
двукратным интегралом

Производя
интегрирование в скобках, имеем,
очевидно,
![]()
Пример 2. Вычислить
площадь области, ограниченной кривыми
![]()

Рис.19
Решение. Определим
точки пересечения данных кривых
(Рис.19). В точке пересечения ординаты
равны, т.е.
![]() ,
,
отсюда![]() Мы
Мы
получили две точки пересечения
![]()
Следовательно,
искомая площадь

5. Вычисление площади поверхности.
Пусть требуется
вычислить площадь поверхности,
ограниченной линией Г (рис.20); поверхность
задана уравнением
![]() где функция
где функция![]() непрерывна и имеет непрерывные частные
непрерывна и имеет непрерывные частные
производные. Обозначим проекцию линии
Г на плоскостьOxy
через L.
Область на плоскости Oxy,
ограниченную линией L,
обозначим D.
Разобьём произвольным
образом область D
на n
элементарных площадок
![]() В
В
каждой площадке![]() возьмём точку
возьмём точку![]() ТочкеPi
ТочкеPi
будет соответствовать на поверхности
точка
![]() Через точкуMi
Через точкуMi
проведём касательную плоскость к
поверхности. Уравнение её примет вид
![]() (1)
(1)
На этой плоскости
выделим такую площадку
![]() ,
,
которая проектируется на плоскостьОху
в виде площадки
![]() .
.
Рассмотрим сумму всех площадок![]()
Предел
![]() этой суммы, когда наибольший из диаметров
этой суммы, когда наибольший из диаметров
площадок![]() –
–
стремится к нулю, мы будем называтьплощадью
поверхности,
т. е. по определению положим
 (2)
(2)
Займемся теперь
вычислением площади поверхности.
Обозначим через
![]()
угол между
касательной плоскостью и плоскостью
Оху.

Рис.20
Рис.21
На основании
известной формулы аналитической
геометрии можно написать (рис.21)
![]()
или
![]() (3)
(3)
Угол
![]() есть в то же время угол между осьюOz
есть в то же время угол между осьюOz
и перпендикуляром к плоскости (1). Поэтому
на основании уравнения (1) и формулы
аналитической геометрии имеем
![]() Следовательно,
Следовательно,
![]()
Подставляя это
выражение в формулу (2), получим

Так как предел
интегральной суммы, стоящей в правой
части последнего равенства, по определению
представляет собой двойной интеграл
![]() то окончательно получаем
то окончательно получаем
![]() (4)
(4)
Это и есть формула,
по которой вычисляется площадь поверхности
![]()
Если уравнение
поверхности дано в виде
![]() или в виде
или в виде![]() то соответствующие формулы для вычисления
то соответствующие формулы для вычисления
поверхности имеют вид
 (3’)
(3’)
 (3’’)
(3’’)
где D’
и D’’
– области на плоскостях Oyz
и Oxz,
в которые проектируется данная
поверхность.
а) Примеры.
Пример 1. Вычислить
поверхность
![]() сферы
сферы
![]()
Решение. Вычислим
поверхность верхней половины сферы
![]() (рис.22). В этом случае
(рис.22). В этом случае
![]()
Следовательно,
подынтегральная функция примет вид
![]()
Область интегрирования
определяется условием
![]() .
.
Таким образом, на основании формулы (4)
будем иметь

Для вычисления
полученного двойного интеграла перейдём
к полярным координатам. В полярных
координатах граница области интегрирования
определяется уравнением
![]() Следовательно,
Следовательно,

Пример2. Найти
площадь той части поверхности цилиндра
![]() которая вырезается цилиндром
которая вырезается цилиндром![]()


Рис.22
Рис.23
Решение. На рис.23
изображена
![]() часть искомой поверхности. Уравнение
часть искомой поверхности. Уравнение
поверхности имеет вид![]() ;
;
поэтому
![]()
![]()
Область интегрирования
представляет собой четверть круга, т.е.
определяется условиями
![]()
Следовательно,
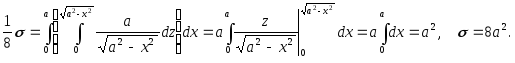
Список использованной
литературы.
-
А.Ф. Бермант ,И.Г.
Араманович
Краткий курс
математического анализа для втузов:
Учебное пособие для втузов: – М.: Наука,
Главная редакция физико-математической
литературы , 1971 г.,736с.
-
Н.С. Пискунов
Дифференциальное
и интегральное исчисления для втузов,
Том 2:
Учебное пособие
для втузов.-13-е изд. -М. :Наука, Главная
редакция физико-математической
литературы, 1985.-560с.
-
В.С. Шипачёв
Высшая
математика: Учебное пособие для втузов:
– М: Наука,
Главная редакция
физико-математической литературы.
Соседние файлы в предмете Алгебра и геометрия
- #
- #
- #
Вычисление площади поверхности с помощью двойного интеграла
Евгений Николаевич Беляев
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Основные формулы
Если везде в области $D$ на координатной плоскости $xOy$ для формулы $I=iint limits _{D}fleft(x,yright)cdot dxcdot dy $ положить $fleft(x,yright)equiv 1$, то, в соответствии со своим геометрическим смыслом, двойной интеграл будет численно равен площади $S$ области интегрирования $D$, то есть $S=iint limits _{D}dxcdot dy $. В полярной системе координат эта же самая формула приобретает вид $S=iint limits _{D^{*} }rho cdot drho cdot dphi $.
Пусть некоторая поверхность $Q$ задана уравнениям $z=f_{1} left(x,yright)$. Вычислим площадь той части поверхности $Q$, которая проецируется на координатную плоскость $xOy$ в область $D_{1} $, где функция $f_{1} left(x,yright)$ непрерывна и имеет непрерывные частные производные. Тогда искомую площадь можно вычислить по формуле $S=iint limits _{D_{1} }sqrt{1+left(frac{partial z}{partial x} right)^{2} +left(frac{partial z}{partial y} right)^{2} } cdot dxcdot dy $.

Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Если уравнение поверхности $Q$ задано в виде $x=f_{2} left(y,zright)$ или $y=f_{3} left(x,zright)$, то соответствующие формулы для вычисления площади поверхности имеют следующий вид:
Здесь $D_{2} $ и $D_{3} $ — области, в которые проецируется поверхность $Q$ на координатные плоскости $yOz$ и $xOz$ соответственно.
Применение формул на практике
Задача 1
Замкнутая область $D$ на плоскости определяется пересечением параболы $y=2cdot x^{2} -16cdot x+31$ с двумя прямыми в точках $A$ и $B$ при $x_{A} =3$ и $x_{B} =6$ соответственно. Эти прямые, в свою очередь, пересекаются в заданной точхе $Cleft(5,9right)$. С помощью двойного интеграла вычислить площадь области $D$, рассматривая её как правильную в направлении оси $Oy$.
- Находим координаты точки $Aleft(x_{A} ,y_{A} right)$:
- Находим координаты точки $Bleft(x_{B} ,y_{B} right)$:
- Находим уравнение прямой $AC$. Она проходит через точки $Aleft(3,1right)$ и $Cleft(5,9right)$. Её уравнение имеет вид $y=a_{1} cdot x+b_{1} $. Угловой коэффициент: $a_{1} =frac{9-1}{5-3} =4$, смещение $b_{1} =1-4cdot 3=-11$. Окончательно $y=4cdot x-11$.
- Находим уравнение прямой $CB$. Она проходит через точки $Cleft(5,9right)$ и $Bleft(6,7right)$. Её уравнение имеет вид $y=a_{2} cdot x+b_{2} $. Угловой коэффициент: $a_{2} =frac{7-9}{6-5} =-2$, смещение $b_{2} =9-left(-2right)cdot 5=19$. Окончательно $y=-2cdot x+19$.
- Заданная область $D$ является правильной в направлении оси $Oy$. Нижняя граница области образована параболой. Верхняя граница области состоит из двух участков: прямой $AC$ и прямой $CB$. Поэтому область $D$ разбиваем на две подобласти (левую $D_{1} $ и правую $D_{2} $) вертикальной прямой, проходящей через точку $C$.
- Площади подобластей определяем с помощью двойного интеграла $S=iint limits _{D}dxcdot dy $. При этом двойной интеграл для каждой подобласти будем вычислять с помощью двукратного интеграла $S=iint limits _{D}dxcdot dy =int limits _{a}^{b}dxcdot int limits _{phi _{1} left(xright)}^{phi _{2} left(xright)}dy $.
- Находим площадь $S_{1} $ левой подобласти $D_{1} $, которая слева ограничена прямой $x=3$, справа — прямой $x=5$, снизу — параболой $y=2cdot x^{2} -16cdot x+31$, сверху — прямой $AC$, уравнение которой $y=4cdot x-11$. Таким образом, $a=3$, $b=5$, $phi _{1} left(xright)=2cdot x^{2} -16cdot x+31$, $phi _{2} left(xright)=4cdot x-11$. Для вычисления площади $S_{1} $ левой подобласти $D_{1} $ окончательно получаем интеграл $S_{1} =int limits _{3}^{5}dxcdot int limits _{2cdot x^{2} -16cdot x+31}^{4cdot x-11}dy $.
- Сначала вычисляем внутренний интеграл $I_{1} $, в котором интегрирование выполняется по $y$, а $x$ считается постоянной:
- Теперь полученную функцию от $x$ следует проинтегрировать по $x$:
- Находим площадь $S_{2} $ правой подобласти $D_{2} $, которая слева ограничена прямой $x=5$, справа — прямой $x=6$, снизу — параболой $y=2cdot x^{2} -16cdot x+31$, сверху — прямой $CB$, уравнение которой $y=-2cdot x+19$. Таким образом, $a=5$, $b=6$, $phi _{1} left(xright)=2cdot x^{2} -16cdot x+31$, $phi _{2} left(xright)=-2cdot x+19$. Для вычисления площади $S_{2} $ правой подобласти $D_{2} $ окончательно получаем интеграл $S_{2} =int limits _{5}^{6}dxcdot int limits _{2cdot x^{2} -16cdot x+31}^{-2cdot x+19}dy $.
- Сначала вычисляем внутренний интеграл $I_{2} $, в котором интегрирование выполняется по $y$, а $x$ считается постоянной:
- Теперь интегрируем по $x$ полученную функцию от $x$:
- Площадь области $D$ равна $S=S_{1} +S_{2} =10,667+4,333=15$ кв.ед.
$y_{A} =2cdot x_{A}^{2} -16cdot x_{A} +31=2cdot 3^{2} -16cdot 3+31=1$. Получаем $Aleft(3,1right)$.
$y_{B} =2cdot x_{B}^{2} -16cdot x_{B} +31=2cdot 6^{2} -16cdot 6+31=7$. Получаем $Bleft(6,7right)$.
[I_{1} =int limits _{2cdot x^{2} -16cdot x+31}^{4cdot x-11}dy =left[yright]_{2cdot x^{2} -16cdot x+31}^{4cdot x-11} =]
[=left(4cdot x-11right)-left(2cdot x^{2} -16cdot x+31right)=-2cdot x^{2} +20cdot x-42.]
[S_{1} =int limits _{3}^{5}I_{1} cdot dx =int limits _{3}^{5}left(-2cdot x^{2} +20cdot x-42right)cdot dx =]
[=-2cdot int limits _{3}^{5}x^{2} cdot dx +20cdot int limits _{3}^{5}xcdot dx -42cdot int limits _{3}^{5}dx =-2cdot left[frac{x^{3} }{3} right]_{3}^{5} +20cdot left[frac{x^{2} }{2} right]_{3}^{5} -42cdot left[xright]_{3}^{5} =]
[=-2cdot frac{1}{3} cdot left[5^{3} -3^{3} right]+20cdot frac{1}{2} cdot left[5^{2} -3^{2} right]-42cdot left[5-3right]=]
[=-frac{2}{3} cdot 98+10cdot 16-42cdot 2approx 10,667.]
[I_{2} =int limits _{2cdot x^{2} -16cdot x+31}^{-2cdot x+19}dy =left[yright]_{2cdot x^{2} -16cdot x+31}^{-2cdot x+19} =]
[=left(-2cdot x+19right)-left(2cdot x^{2} -16cdot x+31right)=-2cdot x^{2} +14cdot x-12.]
[S_{2} =int limits _{5}^{6}I_{2} cdot dx =int limits _{5}^{6}left(-2cdot x^{2} +14cdot x-12right)cdot dx =]
[=-2cdot frac{1}{3} cdot left[6^{3} -5^{3} right]+14cdot frac{1}{2} cdot left[6^{2} -5^{2} right]-12cdot left[6-5right]=]
[=-frac{2}{3} cdot 91+7cdot 11-12cdot 1approx 4,333.]
«Вычисление площади поверхности с помощью двойного интеграла» 👇
Задача 2
На горизонтальной плоскости $xOy$ находится вертикальное цилиндрическое сооружение. Пол сооружения (область $D$) имеет вид прямоугольника с вершинами $Oleft(0,0right)$, $Mleft(5,0right)$, $Kleft(5,7right)$ и $Nleft(0,7right)$. Крыша сооружения имеет вид купола и описывается уравнением $z=sqrt{left(4cdot x+5right)^{3} } +sqrt{left(2cdot y+6right)^{3} } $. Требуется с помощью двойного интеграла вычислить площадь крыши этого сооружения.
- Площадь крыши сооружения вычисляем по формуле $S=int limits _{a}^{b}dxcdot int limits _{phi _{1} left(xright)}^{phi _{2} left(xright)}sqrt{1+left(frac{partial z}{partial x} right)^{2} +left(frac{partial z}{partial y} right)^{2} } cdot dy $. Здесь $z=sqrt{left(4cdot x+5right)^{3} } +sqrt{left(2cdot y+6right)^{3} } $.
- Находим частную производную $frac{partial z}{partial x} $:
- Находим частную производную $frac{partial z}{partial y} $:
- Находим подкоренное выражение интеграла:
- Находим внутренний интеграл:
- Находим площадь крыши:
Его прямоугольный пол является правильным в направлении оси $Oy$. Прямые $x=a$ и $x=b$ ограничивают пол в направлении оси $Ox$ сзади и спереди, следовательно, $a=0$, $b=5$. Линии $phi _{1} left(xright)$ и $phi _{2} left(xright)$ ограничивают пол в направлении оси $Oy$ слева и справа, следовательно, $phi _{1} left(xright)=0$, $phi _{2} left(xright)=7$. Окончательно $S=int limits _{0}^{5}dxcdot int limits _{0}^{7}sqrt{1+left(frac{partial z}{partial x} right)^{2} +left(frac{partial z}{partial y} right)^{2} } cdot dy $.
[frac{partial z}{partial x} =frac{partial left(sqrt{left(4cdot x+5right)^{3} } +sqrt{left(2cdot y+6right)^{3} } right)}{partial x} =frac{partial sqrt{left(4cdot x+5right)^{3} } }{partial x} =6cdot sqrt{4cdot x+5} .]
[frac{partial z}{partial y} =frac{partial left(sqrt{left(4cdot x+5right)^{3} } +sqrt{left(2cdot y+6right)^{3} } right)}{partial y} =frac{partial sqrt{left(2cdot y+6right)^{3} } }{partial y} =3cdot sqrt{2cdot y+6} .]
[W=1+left(frac{partial z}{partial x} right)^{2} +left(frac{partial z}{partial y} right)^{2} =144cdot x+18cdot y+235.]
Таким образом, для нахождения площади нужно вычислить интеграл
[S=int limits _{0}^{5}dx int limits _{0}^{7}sqrt{W} cdot dy =int limits _{0}^{5}dx int limits _{0}^{7}sqrt{144cdot x+18cdot y+235} cdot dy .]
[I=int limits _{0}^{7}sqrt{144cdot x+18cdot y+235} cdot dy =frac{1}{27} cdot left(144cdot x+361right)^{frac{3}{2} } -frac{1}{27} cdot left(144cdot x+235right)^{frac{3}{2} } .]
[S=int limits _{0}^{5}Icdot dx =frac{1}{27} cdot int limits _{0}^{5}left(144cdot x+361right)^{frac{3}{2} } cdot dx -frac{1}{27} cdot int limits _{0}^{5}left(144cdot x+235right)^{frac{3}{2} } cdot dx ;]
[I_{1} =int limits _{0}^{5}left(144cdot x+361right)^{frac{3}{2} } cdot dx =left[frac{1}{144} cdot frac{left(144cdot x+361right)^{frac{5}{2} } }{frac{5}{2} } right]_{0}^{5} approx 99845,86;]
[I_{2} =int limits _{0}^{5}left(144cdot x+235right)^{frac{3}{2} } cdot dx =left[frac{1}{144} cdot frac{left(144cdot x+235right)^{frac{5}{2} } }{frac{5}{2} } right]_{0}^{5} approx 75938,31;]
окончательно $S=frac{1}{27} cdot left(99845,86-75938,31right)approx 885,46$ кв.ед.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 19.01.2023
Вычисление площади поверхности
Пример 1
Пусть в пространстве задана кусочно-гладкая поверхность $sigma $, однозначно проектирующаяся в область $mathbf { textit { D } } $ на плоскости $mathbf { textit { Оху } } $. Пусть эта поверхность задаётся уравнением $sigma :;z=f(x,y),;(x,y)in D$. Тогда площадь этой поверхности выражается формулой
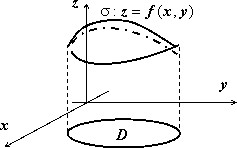
$ s(sigma )=iintlimits_D { sqrt { 1+left( { frac { partial f } { partial x } }right)^2+left( { frac { partial f } { partial y } }right)^2 } dxdy } . $
Мы докажем эту формулу позже, когда будем изучать поверхностные интегралы. Сейчас рассмотрим пример: найти площадь лепестков, вырезаемых цилиндром $mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } $ = 2$mathbf { textit { ax } } $ из сферы $mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } +mathbf { textit { z } } ^ { 2 } $ = 4$mathbf { textit { a } } ^ { 2 } $ .
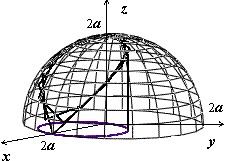
Решение:
На рисунке изображён верхний из этих лепестков. Уравнение поверхности $z=sqrt { 4a^2-x^2-y^2 } ,$ вычисляем производные $frac { partial z } { partial x } =-frac { x } { sqrt { 4a^2-x^2-y^2 } } , quad frac { partial z } { partial y } =-frac { y } { sqrt { 4a^2-x^2-y^2 } } ,$ и $s(sigma )=iintlimits_D { sqrt { 1+frac { x^2+y^2 } { 4a^2-x^2-y^2 } dxdy } } =2aiintlimits_D { frac { dxdy } { sqrt { 4a^2-x^2-y^2 } } } $.
Область $mathbf { textit { D } } $ – сдвинутый на $mathbf { textit { а } } $ единиц по оси $mathbf { textit { Ох } } $ круг, поэтому вычисляем в полярных координатах, учитывая симметрию поверхности относительно плоскостей $mathbf { textit { Оху } } $ и $mathbf { textit { Охz } } $:
$s(sigma )=4cdot 2aiintlimits_ { D_ { r,varphi } } { frac { rdrdvarphi } { sqrt { 4a^2-r^2 } } } =8aintlimits_0^ { pi /2 } { dvarphi intlimits_0^ { 2acos varphi } { left( { 4a^2-r^2 }right)^ { -1/2 } rdr } } =-8aintlimits_0^ { pi /2 } { dvarphi left. { left( { 4a^2-r^2 }right)^ { 1/2 } }right|_0^ { 2acos varphi } } = \ =8aintlimits_0^ { pi /2 } { left[ { 2a-2asqrt { 1-cos ^2varphi } }right]dvarphi } =16a^2left. { left( { varphi +cos varphi }right) }right|_0^ { pi /2 } =16a^2left( { pi /2-1 }right)$.
Пример 2
Вычислить площадь cферы радиуса (a.)
Решение:
Рассмотрим верхнюю полусферу. Ее уравнение имеет вид $ { { x^2 } + { y^2 } + { z^2 } = { a^2 } } ;; { text { или } ;;z = sqrt { { a^2 } – { x^2 } – { y^2 } } . } $
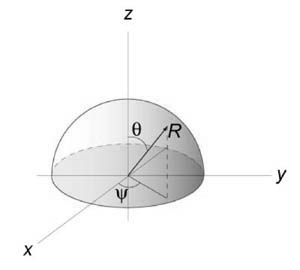
Очевидно, область интегрирования (R) представляет собой круг с таким же радиусом (a,) расположенный в центре координат. Площадь полусферы вычисляется по формуле $ { S_ { largefrac { 1 } { 2 } normalsize } } = iintlimits_R { sqrt { 1 + { { left( { frac { { partial z } } { { partial x } } }right) } ^2 } + { { left( { frac { { partial z } } { { partial y } } }right) } ^2 } } dxdy } .$
Найдем частные производные. $ { frac { { partial z } } { { partial x } } } = { frac { partial } { { partial x } } sqrt { { a^2 } – { x^2 } – { y^2 } } } = { frac { { – { 2 } x } } { { { 2 } sqrt { { a^2 } – { x^2 } – { y^2 } } } } } = { – frac { x } { z } , } $ $ { frac { { partial z } } { { partial y } } } = { frac { partial } { { partial y } } sqrt { { a^2 } – { x^2 } – { y^2 } } } = { frac { { – { 2 } y } } { { { 2 } sqrt { { a^2 } – { x^2 } – { y^2 } } } } } = { – frac { y } { z } . } $
Подставляя найденные производные, получаем $ { { S_ { largefrac { 1 } { 2 } normalsize } } = iintlimits_R { sqrt { 1 + { { left( { frac { { partial z } } { { partial x } } }right) } ^2 } + { { left( { frac { { partial z } } { { partial y } } }right) } ^2 } } dxdy } } = { iintlimits_R { sqrt { 1 + frac { { { x^2 } } } { { { z^2 } } } + frac { { { y^2 } } } { { { z^2 } } } } dxdy } } = { iintlimits_R { sqrt { frac { { { z^2 } + { x^2 } + { y^2 } } } { { { z^2 } } } } dxdy } } = { iintlimits_R { frac { a } { z } dxdy } . } $
Преобразуем двойной интеграл в полярные координаты. $ { { S_ { largefrac { 1 } { 2 } normalsize } } = iintlimits_R { frac { a } { z } dxdy } } = { intlimits_0^ { 2pi } { intlimits_0^a { frac { a } { { sqrt { { a^2 } – { r^2 } } } } rdrdtheta } } } = { aintlimits_0^ { 2pi } { dtheta } intlimits_0^a { frac { { rdr } } { { sqrt { { a^2 } – { r^2 } } } } } } = { – 2pi aintlimits_0^a { frac { { dleft( { { a^2 } – { r^2 } }right) } } { { 2sqrt { { a^2 } – { r^2 } } } } } } = { – 2pi aleft. { left( { sqrt { { a^2 } – { r^2 } } }right) }right|_ { r = 0 } ^a } = { – 2pi aleft( { 0 – a }right) = 2pi { a^2 } . } $
Площадь поверхности полной сферы, соответственно, равна $S = 2 { S_ { largefrac { 1 } { 2 } normalsize } } = 4pi { a^2 } .$
