Каждому из нас нередко приходилось считать площадь решётчатого многоугольника (изображённого, например, на клетчатой бумаге). В основном, это делают ещё по известным со школы формулам. Но в этом случае для каждой фигуры приходится помнить выражение её площади.
Не легче ли использовать одну формулу для всех многоугольников?
— Сказка? — Нет, теорема Пика!
• Названа она в честь Георга Пика (нет, не оружия или покемона), доказавшего её в 1899 году.
Формулировка звучит так:
S = В + Г / 2 − 1, где S — площадь многоугольника, В — количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.
• Важное замечание: формула справедлива только для многоугольников, у которых вершины расположены в узлах решетки.
Например, для многоугольника на рисунке, В=7 (красные точки), Г=8 (зелёные точки), поэтому S = 7 + 8/2 – 1 = 10 квадратных единиц.

Докажем теорему Пика:
• Рассмотрим прямоугольник со сторонами, лежащими на линиях решетки. Пусть длины его сторон равны a и b. Имеем в этом случае В = (a-1)(b-1), Г = 2a+2b и, по формуле Пика, S = (a-1)(b-1)+a+b-1 = ab .
• Рассмотрим теперь прямоугольный треугольник с катетами, лежащими на осях координат. Такой треугольник получается из прямоугольника со сторонами a и b, рассмотренного в предыдущем случае, разрезанием его по диагонали. Пусть на диагонали лежат c целочисленных точек. Тогда для этого случая В = ((a-1)(b-1)-c+2)/2, Г = (2a+2b)/2+c-1 и получаем, что S = ab/2.
• Теперь рассмотрим произвольный треугольник. Его можно получить, отрезав от прямоугольника несколько прямоугольных треугольников (см. рисунок). Поскольку и для прямоугольника, и для прямоугольного треугольника формула Пика верна, мы получаем, что она будет справедлива и для произвольного треугольника.

• Остается сделать последний шаг: перейти от треугольников к многоугольникам. Любой многоугольник можно триангулировать, т.е. разбить на треугольники (например, диагоналями). Отсюда по индукции следует, что формула Пика верна для любого многоугольника. чтд
К сожалению, эта столь простая и красивая формула плохо обобщается на высшие размерности.
Наглядно показал это Рив, предложив в 1957 г. рассмотреть тетраэдр (называемый теперь тетраэдром Рива) со следующими вершинами:
A(0,0,0), B(1,0,0), C(0,1,0), D(1,1,k)
Тогда этот тетраэдр ABCD при любых k не содержит внутри ни одной точки с целочисленными координатами, а на его границе — лежат только четыре точки A, B, C, D. Таким образом, объём и площадь поверхности этого тетраэдра могут быть разными, в то время как число точек внутри и на границе — неизменны; следовательно, формула Пика не допускает обобщений даже на трёхмерный случай.
Тем не менее, некоторое подобное обобщение на пространства большей размерности всё же имеется, — это многочлены Эрхарта, но они весьма сложны, и зависят не только от числа точек внутри и на границе фигуры.

Специально для ЖЖ матфака, Сергей Романов.
У этого термина существуют и другие значения, см. Теорема Пика.
Формула Пи́ка (или теорема Пи́ка) — классический результат комбинаторной геометрии и геометрии чисел,
даёт выражение для площади многоугольника с целочисленными вершинами.
Названа в честь Георга Пика, доказавшего её в 1899 году.
Формулировка[править | править код]

В = 7, Г = 8,
В + Г/2 − 1 = 10
Площадь многоугольника с целочисленными вершинами[1] равна

где В — количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.
Следствия[править | править код]
- Площадь треугольника с вершинами в узлах и не содержащего узлов ни внутри, ни на сторонах (кроме вершин), равна 1/2.
- Этот факт даёт геометрическое доказательство формулы для разности подходящих дробей цепной дроби.
Вариации и обобщения[править | править код]

Контрпример к аналогу теоремы Пика в размерности 3.
- Многочлен Эрара даёт один из вариантов обобщения формулы Пика на старшие размерности.
- где суммирование ведётся по всем целочисленным точкам
и
телесный угол
при
; если
лежит внутри
, то считается что
.[2]
-
- где
обозначает площадь единичной сферы в
.
-
Примечания[править | править код]
- ↑ Точка координатной плоскости называется целочисленной, если обе её координаты целые.
- ↑ Tabachnikov, Sergei, Pierre Deligne, and Sinai Robins. The Ice Cube Proof (англ.) // The Mathematical Intelligencer. — 2014. — Vol. 36, no. 4. — P. 1-3.
Литература[править | править код]
- В. В. Прасолов. Задачи по планиметрии. — М.: МЦНМО, 2001. — 584 с. — ISBN 5-900916-82-0.
- А. Кушниренко. Целые точки в многоугольниках и многогранниках // Квант. — 1977. — № 4. — С. 13—20.
Приветствую Вас, уважаемые Читатели! Сегодня хочу рассказать Вам о формуле, которая настолько упрощает решение некоторых задач единого государственного экзамена по математике, что не пользоваться её было бы кощунством. Речь идет о задачах, в которых надо найти площадь многоугольников, начерченных на бумаге в клетку. Поехали!
Итак, необходимо найти площадь многоугольника из рисунка ниже (2 фото):
Да, решение не сложное, но, оказывается, есть намного более короткий путь, который изобрел австрийский математик Георг Пик:
Давайте еще раз внимательно посмотрим на условие задачи:
По формуле Пика необходимо подсчитать количество точек целочисленной решетки внутри фигуры (синим цветом) и на границах фигуры (красным цветом). Таких точек получается по 10 штук. Дальше площадь рассчитывается по формуле:
S = В + Г/2 – 1 = 10 + 10/2 – 1 = 14, где В – точки внутри, Г – на границе.
Без сомнения чудесная формула, однако она работает лишь тогда, когда все вершины многоугольника расположены на узлах решетки, так что знание формул площадей из геометрии всё равно не будет лишним. А что думаете по этому поводу Вы? Пишите в комментариях. Спасибо за внимание!
Читайте также:
- Кирпич Эйлера
- Самый важный из интегралов
- TELEGRAM и Facebook – там я публикую не только интересные статьи, но и математический юмор и многое другое.
Вокруг формулы Пика
Уровень сложности
Средний
Время на прочтение
2 мин
Количество просмотров 2.2K
Как найти площадь произвольного многоугольника с вершинами в узлах клетчатой бумаги?
В простых ситуациях его можно разбить на треугольники (рис. 1а) или, наоборот, достроить до прямоугольника (рис. 1б). Но как быть в общем случае? Посмотрите, скажем, на рисунок 1в.

Оказывается, достаточно подсчитать числовершин внутри многоугольника и число
на его границе — тогда его площадь
будет равна
Это формула называется формулой Пика в честь австрийского математика Георга Пика (1859–1942), открывшего её в 1899 году. Так, для многоугольника на рисунке 1в имеем
,
, поэтому
Формула выглядит удивительно просто. Интересно, столь же просто её доказать?
Этап 1: ШАГ ИНДУКЦИИ. Предположим, что многоугольник разбит диагональю на два, для которых формула доказана. Тогда несложно показать, что она верна и для.
Этап 2: ТРИАНГУЛЯЦИЯ. Многократно проводя внутренние диагонали, разобьём наш многоугольник на элементарные треугольники (не содержащие узлов ни на границе, ни внутри, кроме вершин). Для такого треугольникаи
поэтому площадь должна быть равна
Этап 3: БАЗА ИНДУКЦИИ. Остаётся доказать, что площадь элементарного треугольника равнаМы приведём важное и красивое рассуждение.
Пусть треугольник имеет вершины и
Достроим его до параллелограмма, добавив вершину
и замостим его копиями всю плоскость (рис. 2).
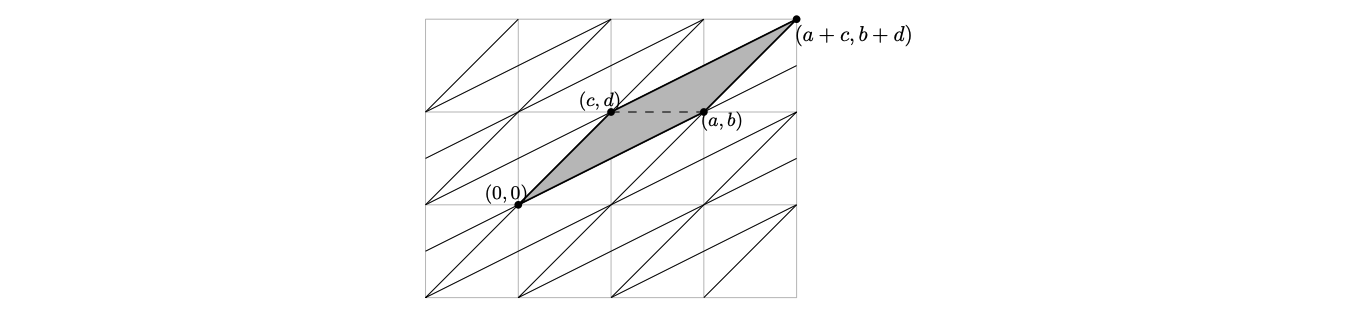
Элементарность нашего треугольника равносильна тому, что любой узелможно получить из узла
целочисленными сдвигами сторон
и
Иными словами, для любых целых
и
найдутся целые
и
такие, что
Неожиданно, геометрическая задача свелась к чисто алгебраической — системе линейных уравнений. Её решение даётся формулами Крамера
Хорошо известно, что определительпо модулю равен площади параллелограмма, построенного на векторах
и
поэтому нам надо доказать, что
Приимеем
а при
Так как
всегда должны быть целыми, то
кратны
откуда
кратно
, что возможно, лишь при
Формула Пика доказана.
В заключение сделаем несколько замечаний.
-
Приведённое рассуждение с замещением плоскости на школьном языке иллюстрирует важные идеи высшей алгебры — описание базисов свободной абелевой группы
и группы её автоморфизмов:
-
Последний факт можно обобщить на высшие размерности:
-
А вот формула Пика неверна уже в трёхмерном пространстве: объём многогранника с целыми вершинами не выражается через количества вершин внутри, на гранях и рёбрах.
-
Вместе с тем существуют варианты обобщения формулы Пика для некоторых классов целочисленных многомерных многогранников (например, с центрально-симметричными гранями).
Автор: Андрей Канунников, к. ф.-м. н., мехмат МГУ, преподаватель ШАД Хелпер
Григорий Мерзон
«Квантик» №9, 2018
Формула Пика
Как найти площадь многоугольника на клетчатой бумаге? Можно подсчитать число клеток, которые полностью накрыты фигурой, и ещё как-то учесть клетки, накрытые фигурой частично, — скажем, прибавить половину от числа этих клеток. И сказать, что площадь фигуры (в клеточках) приблизительно равна полученной сумме.

А можно вместо клеток, полностью или частично накрытых многоугольником, считать узлы сетки (вершины клеток) строго внутри многоугольника или на его границе.

Действительно, вокруг каждого узла сетки можно нарисовать по единичному квадратику. И если узел лежит на границе многоугольника, то этот квадратик накрыт многоугольником только частично. А если узел лежит внутри, то обычно и квадратик накрыт многоугольником полностью… впрочем, иногда всё же не полностью — но мы и считаем площадь только приближённо.
Но чудесным образом последний рецепт всегда даёт почти правильный ответ! А именно, верна Формула Пика. Площадь S многоугольника с вершинами в узлах сетки можно найти по формуле
S
=
i
+
b
2
−
1
,
где i — число узлов сетки строго внутри многоугольника, b — число узлов сетки на его границе.
Подчеркнём, что это уже не приближённая, а точная формула!

Интересно, что хотя длины сторон у многоугольников обычно совершенно не целые, формула Пика гарантирует, что площадь всегда получится целой или полуцелой.

Тающий лёд
Формула Пика известна с XIX века, и с тех пор у неё появилось много доказательств, но большинство из них не такие уж простые. Мы обсудим предложенный в 1997 году швейцарским математиком Кристианом Блаттером мысленный эксперимент с тающим льдом, который сразу объясняет формулу Пика.

Поставим на каждый узел сетки по одинаковому цилиндрическому столбику изо льда. Каждый столбик очень тонкий (пересекается только с теми сторонами многоугольника, которые проходят через центр столбика) и весит 1 грамм.
Построим вокруг каждого столбика забор в виде единичного квадратика, после чего растопим весь лёд (во всех квадратиках вода растекается одинаково и симметрично относительно центра своего квадратика). Вся клетчатая плоскость будет равномерно залита водой, и в каждой ячейке площади 1 будет по 1 грамму воды. То есть количество воды в нашем многоугольнике (в граммах) будет равно его площади (в клетках).

С другой стороны, задумаемся, откуда эта вода попала в наш многоугольник. Посмотрим на какую-нибудь конкретную сторону многоугольника. Если через неё внутрь многоугольника втекла вода из какого-то столбика, то точно столько же воды из симметричного столбика (симметричного относительно середины этой стороны) через неё из многоугольника вытекло.

То есть внутри многоугольника ровно столько воды, сколько в нём было льда! А сколько в нём было льда? Каждый из узлов сетки внутри многоугольника даёт вклад 1 грамм, общий вес получается i граммов. Узлы на сторонах обычно дают по
1
2
грамма, но только если это не вершина, для вершины этот вес меньше — так что и общий вес узлов на границе получается не
b
2
граммов, а меньше.

Насколько меньше? Продлим немного каждую сторону, обходя многоугольник вдоль сторон по часовой стрелке. На рисунке ниже красная часть дополняет каждую из синих частей до половины круга. Но красные части в сумме дают ровно один круг! Ведь, обходя многоугольник по контуру, мы в каждой вершине поворачиваемся на угол, соответствующий красной части, пока не вернёмся в исходную точку, сделав как раз полный оборот.

То есть суммарный вес льда внутри многоугольника равен
i
+
b
2
−
1
, и мы получили формулу Пика!
Художник Мария Усеинова

