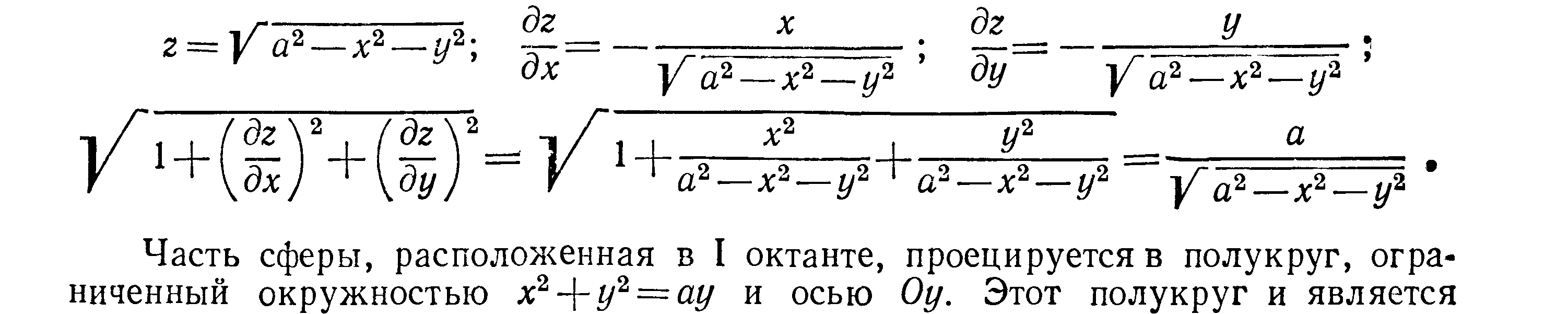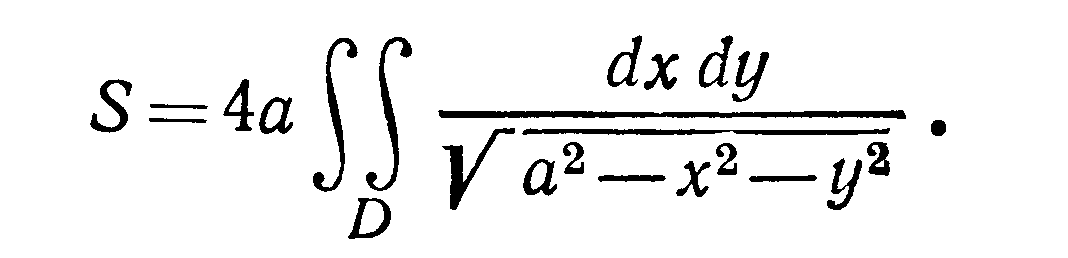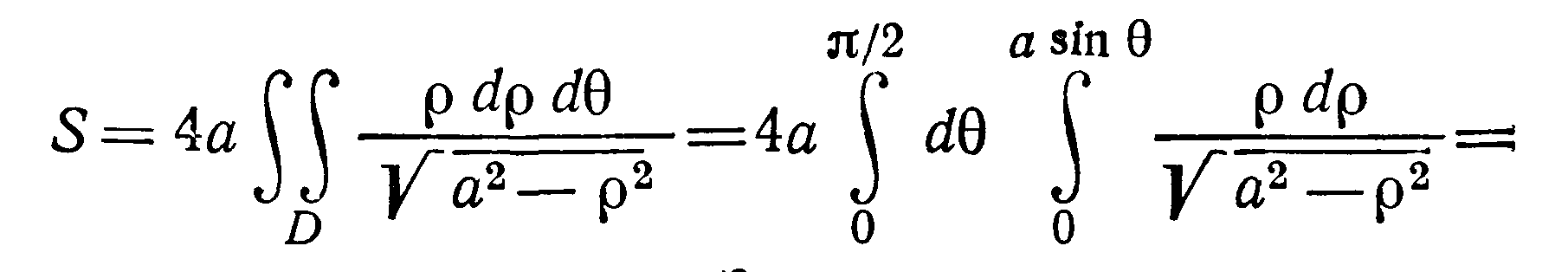Как найти площадь фигуры с вырезанной частью

На этой странице сайта вы найдете ответы на вопрос Как найти площадь фигуры, если это прямоугольник с вырезанным куском?,
относящийся к категории Математика. Сложность вопроса соответствует базовым
знаниям учеников 1 – 4 классов. Для получения дополнительной информации
найдите другие вопросы, относящимися к данной тематике, с помощью поисковой
системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и
задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям.
Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы
помогут найти нужную информацию.

Знаете ответ?

Математика

5 класс

Урок №30

Площадь прямоугольника. Единицы площади

Перечень рассматриваемых вопросов:

– понятие площади фигуры;

-единицы измерения площади; 

– площадь прямоугольника, квадрата; 

– приближенное измерение площади фигуры на клетчатой бумаге.

Тезаурус

Прямоугольник – четырёхугольник, у которого все углы прямые (равны 90 градусам). 

Квадрат – прямоугольник, у которого все стороны равны. 

Площадь прямоугольника– число, которое показывает, сколько квадратных единиц содержится в прямоугольнике.

Основная литература

Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений.// С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

Дополнительная литература

1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы.// И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

Сегодня мы начнём занятие с задачи. Представим, что две девочки пришли в магазин, чтобы купить в подарок подруге на день рождения коробку конфет. На витрине были разложены самые разные наборы сладостей. Девочки решили купить ту коробку, которая больше. А какая из них больше? Как это измерить? Можно сравнить коробки по длине и ширине или просто положить их друг на друга. Но одна коробка оказалась длиннее, а другая – шире. Какая же из них больше? Как это узнать?

Чтобы ответить на эти вопросы, мы поговорим о вычислении площади прямоугольника.

Для начала введём понятие площади фигуры.

Если какую-нибудь площадь можно разбить на n квадратов со стороной, например, 1 см, то получится, что площадь фигуры равна n см².

За единицу измерения площадей принимают не только квадратный сантиметр, но и квадратный миллиметр, квадратный дециметр, квадратный метр.

Это площади квадратов, длины сторон которых равны одному миллиметру, одному дециметру и одному метру соответственно.

Далее покажем, что подразумевается под площадью прямоугольника.

Площадью прямоугольника называют число, которое показывает, сколько квадратных единиц содержится в прямоугольнике.

Называя величину площади, необходимо указывать единицу измерения.

Например, прямоугольник состоит из пятнадцати квадратов; площадь каждого квадрата составляет 1 см². Следовательно, площадь всего прямоугольника равна 15 см².

S = 15 см²

Решим задачу.

Найдём площадь прямоугольника ABCD, который имеет длину АВ = 6 см и ширину ВС = 7 см. Для этого разделим его на квадратные сантиметры. Сосчитаем, сколько квадратных сантиметров в нём содержится.

В прямоугольнике ABCD квадратный сантиметр содержится сорок два раза – значит, его площадь равна: S = 42 см² = 6 см · 7 см = АВ · ВС.

Поэтому можно ввести формулу для нахождения площади прямоугольника.

Чтобы найти площадь прямоугольника S, нужно умножить его длину a на ширину b.

S = а · b

Так как квадрат является прямоугольником, у которого все стороны равны, то его площадь можно вычислить как квадрат его стороны а.

S = а · а = а²

Далее найдём соотношение между единицами измерения площадей.

Так как 1 см = 10 мм, следовательно, 1 см² = 10² мм² = 100 мм².

Соответственно, 1 дм² = 10² см² = 100 см²

1 м² = 10² дм² = 100 дм²

1 км² = 1000² м² = 1000000 м².

Для измерения небольших площадей земельных участков используют специальную единицу измерения– ар, которая равна площади квадрата со стороной десять метров. В обиходе ар называют соткой, так как один ар– это сто квадратных метров.

1 ар = 10² м² = 100 м²

Для обмера больших земельных территорий ввели единицу один гектар, которая соответствует площади квадрата со стороной сто метров.

1 га = 100² м² = 10000 м² = 100 а

Решим задачу.

Найдём площадь прямоугольника.

При измерении окажется, что стороны с недостатком приближенно равны трём и пяти сантиметрам. Значит, площадь прямоугольника больше, чем произведение этих сторон, то есть пятнадцати квадратных сантиметров.

S (с недостатком) = 3 · 5 = 15 см²

Если взять стороны в приближении с избытком, то есть четыре и шесть сантиметров, то площадь будет меньше произведения сторон, а именно равна двадцати четырём квадратным сантиметрам.

S (с избытком) = 4 · 6 = 24 см²

Таким образом, площадь этого прямоугольника варьируется от пятнадцати до двадцати четырёх квадратных сантиметров.

15 см² < S < 24 см²

Отметим, что равные прямоугольники имеют равную площадь.

Сравним площади закрашенных квадратов, изображённых на рисунке.

Решение: если посмотреть внимательно на рисунок, то можно заметить, что все фигуры расположены в одинаковых квадратах со стороной 9 клеток, следовательно, площади этих квадратов одинаковы. На верхнем рисунке шесть фигур – два квадрата и четыре треугольника. На нижнем рисунке пять фигур – квадрат и четыре треугольника.

Далее внимательно посмотрим на треугольники – все они одинаковы, следовательно, их площади одинаковы. И, если из больших квадратов, в которых расположены наши фигуры, мы отнимем сумму площадей равных треугольников, получится, что площади оставшихся фигур (квадратов) верхней и нижней части равны.

Примеры заданий из Тренировочного модуля

№ 1. В квадрате все стороны равны 5 см. Чему равна площадь квадрата?

Решение: Для нахождения площади квадрата воспользуемся следующей формулой:

S = а² = 5см · 5 см = 25 см²

№ 2. Найдите площадь фигуры.

Решение: сначала следует разделить фигуру на три прямоугольника, далее найти площадь каждого по формулеS=а · b, а затем сложить площади трёх фигур. Или можно найти площадь прямоугольника со сторонами 10 см и 3 см, она равна 30 см². Далее вычислить площадь вырезанной фигуры со сторонами 2см на 1 см, она составляет 2см². И вычесть 2 см² из 30см².

Ответ: 28 см².

Задачи с решениями

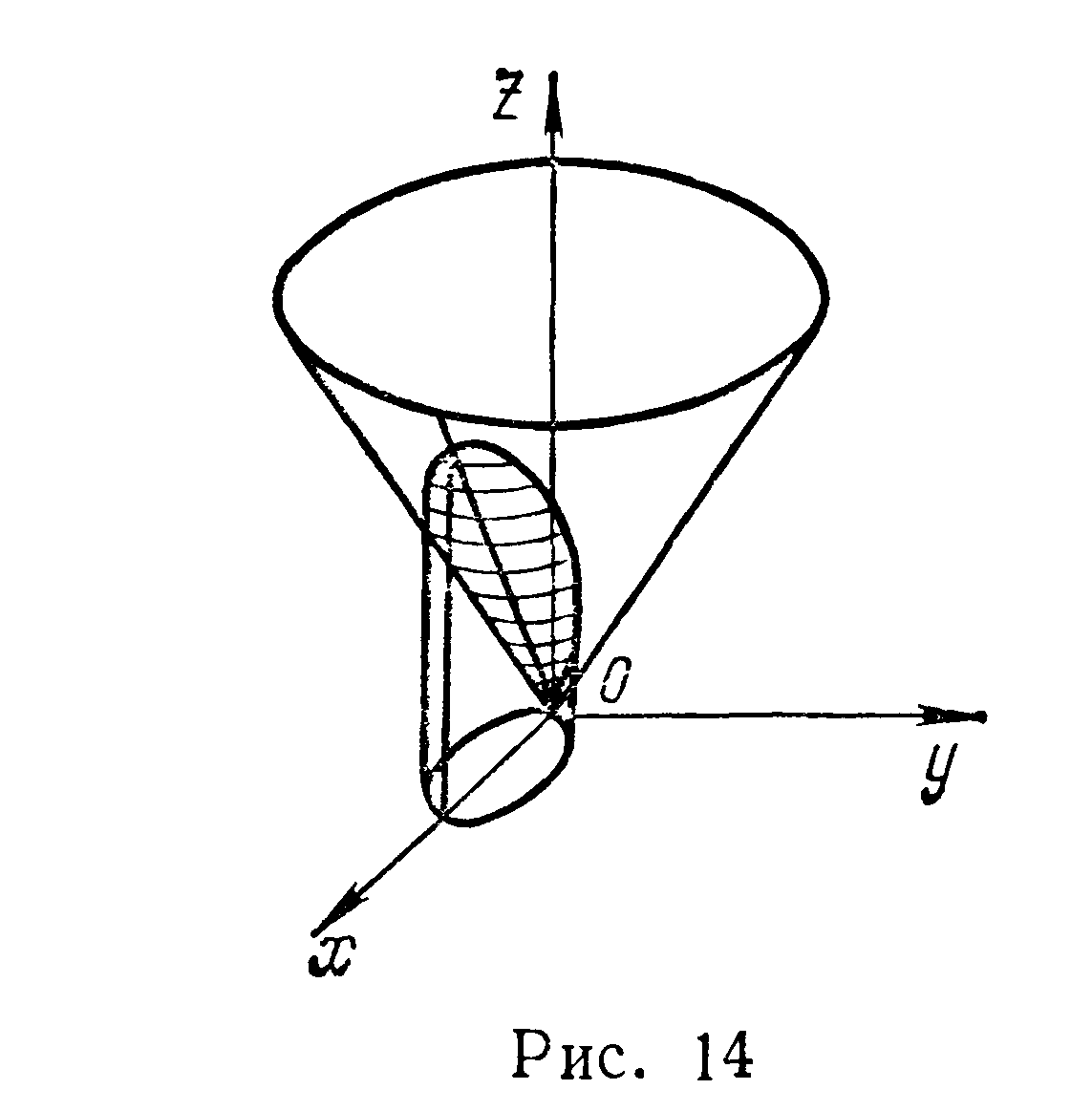
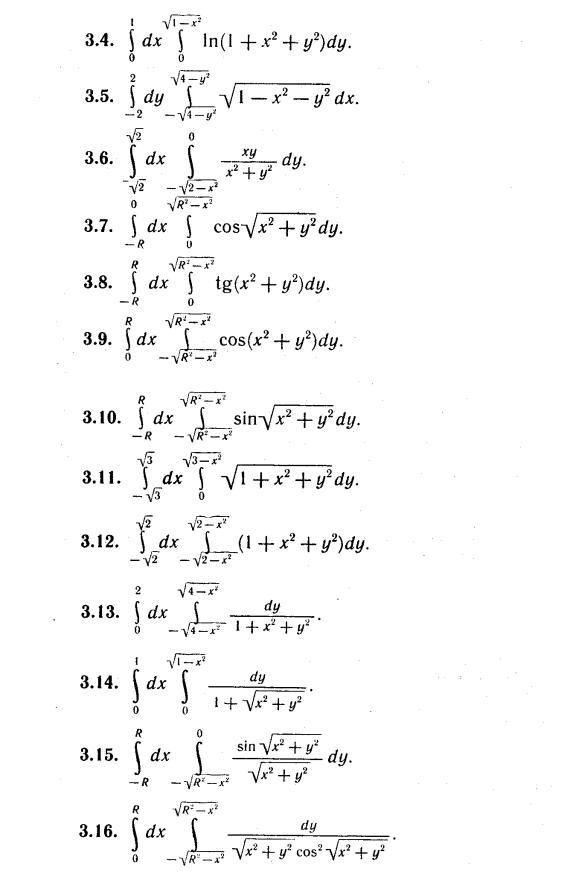
1. Найти площадь части сферы
   

   заключенной внутри цилиндра
   

Решение Из уравнения сферы имеем
(для I октанта):

областью интегрирования D.
Поверхность расположена в четырех
октантах потому искомая площадь

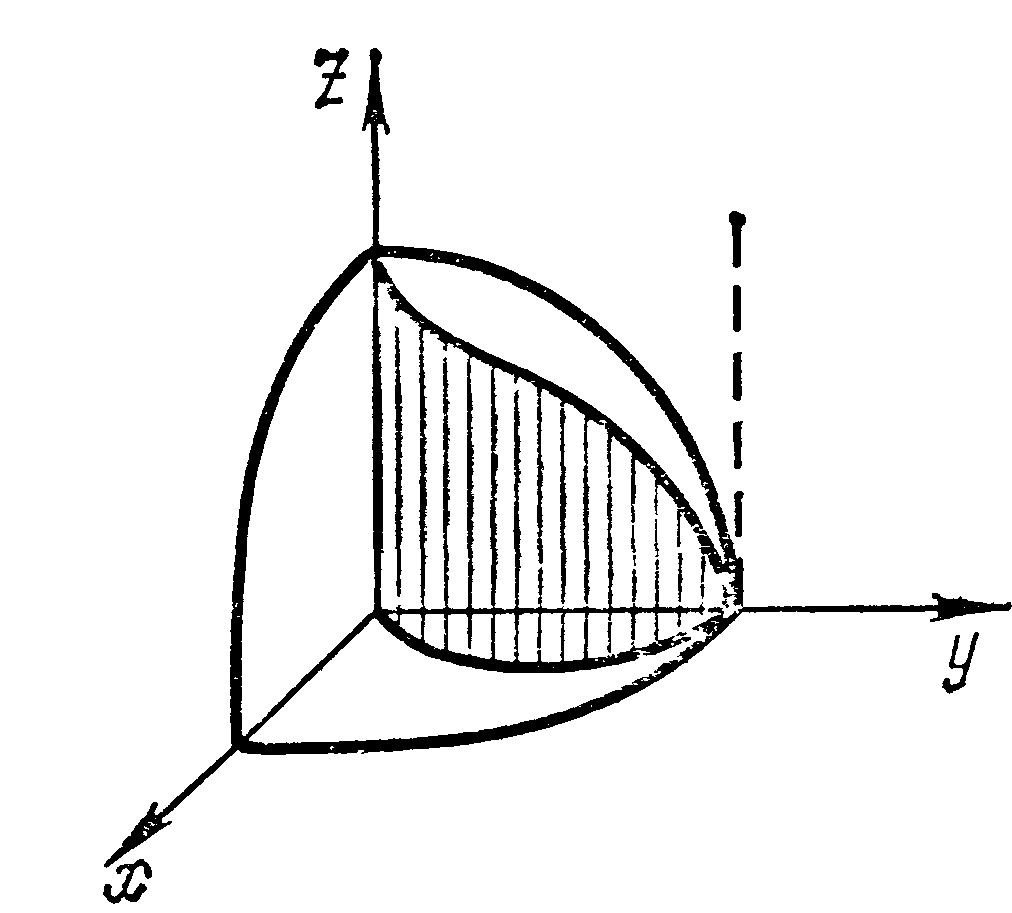
Перейдем к полярным координатам, тогда
уравнение окружности примет вид

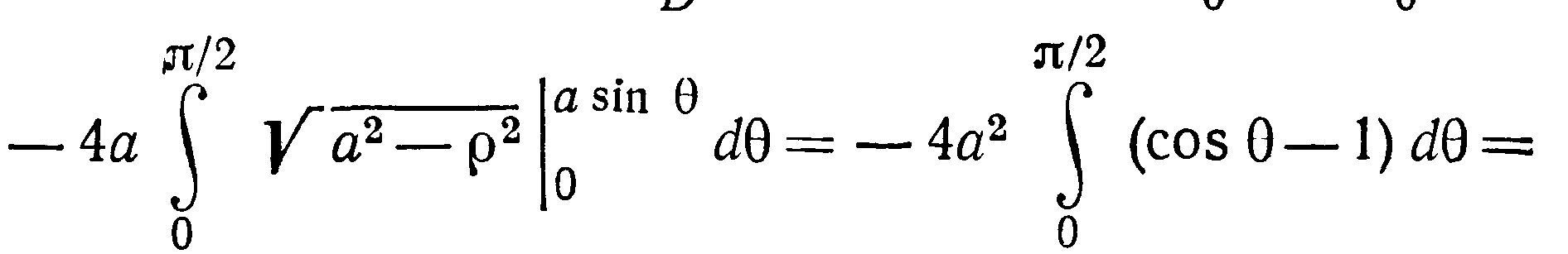
1. Найти площадь части конуса
   

   внутри цилиндра
   

Решение Из уравнения конуса
имеем

Областью
интегрирования D является круг,
ограниченный окружностью

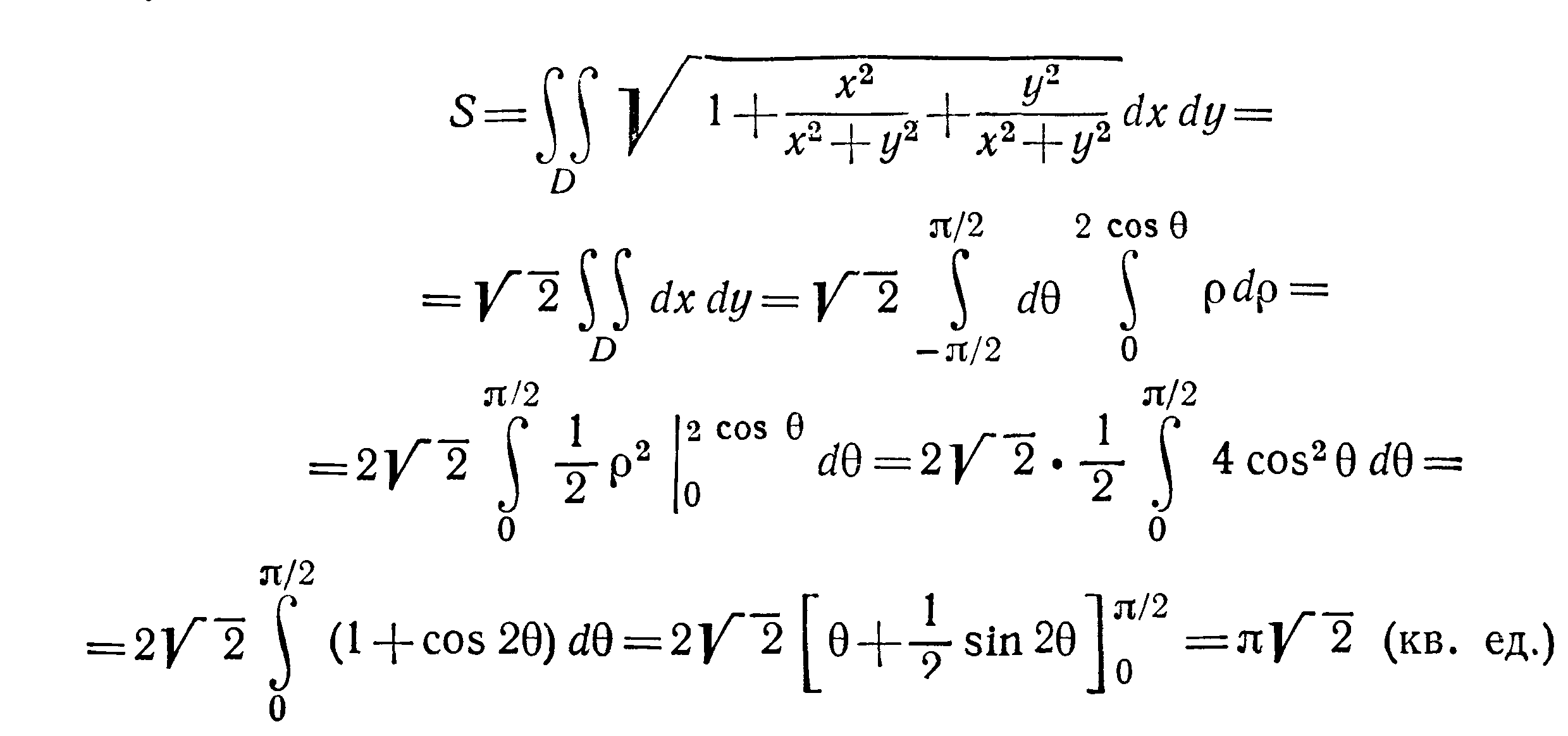
1. Вычислить площадь поверхности цилиндра

   

   отсеченной плоскостями
   

Решение Областью интегрирования
служит треугольник ОАВ. Из уравнения
цилиндра имеем

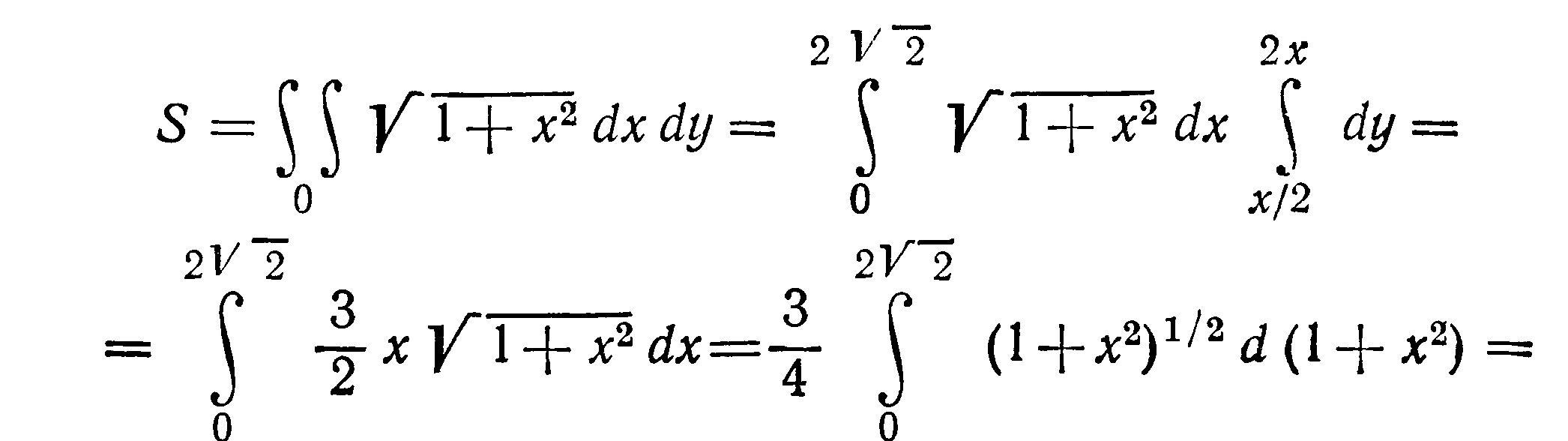
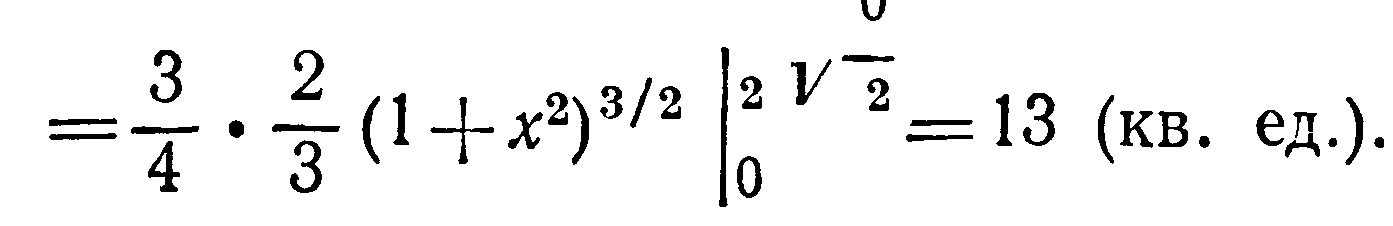
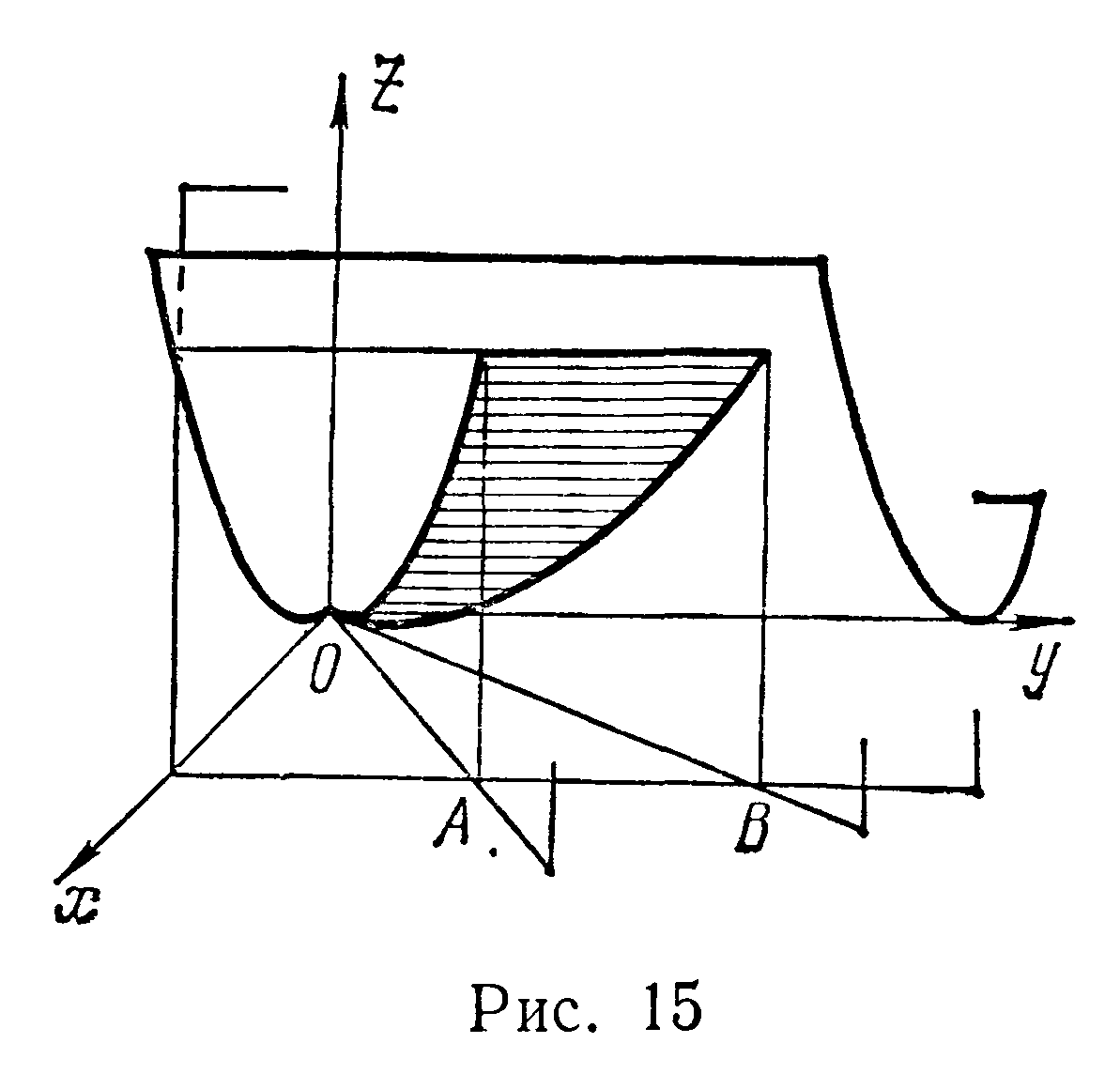
1. Вычислить площадь части поверхности
   параболоида x
   
   ,
   вырезанной цилиндром
   

Решение Область интегрирования
– окружность

(она расположена в плоскости yOz).
Из уравнения параболоида имеем

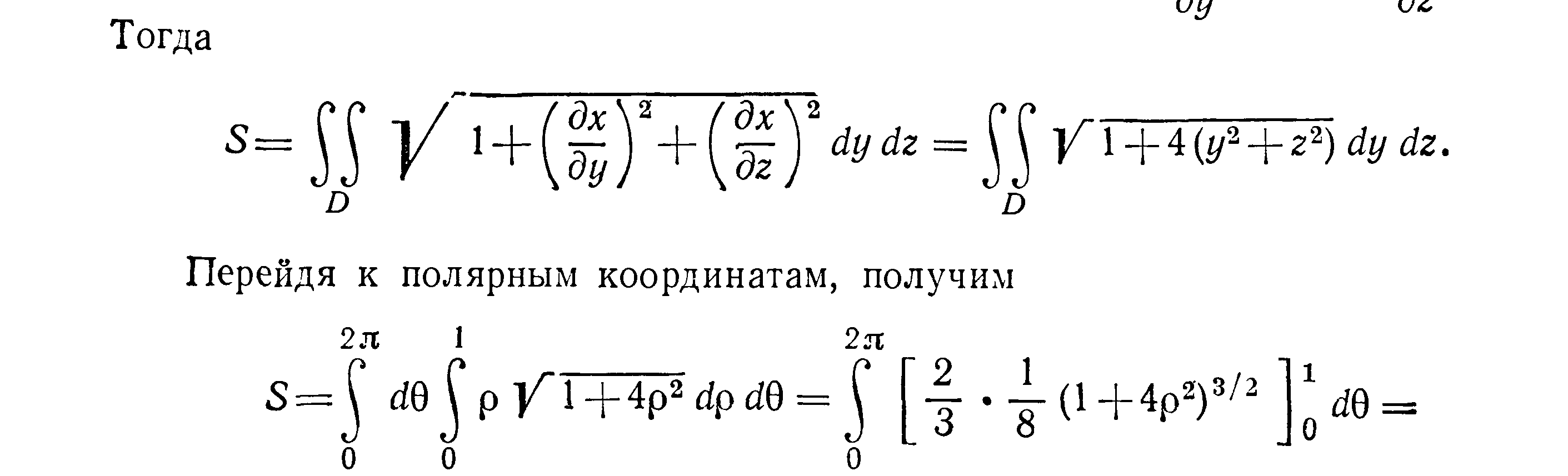
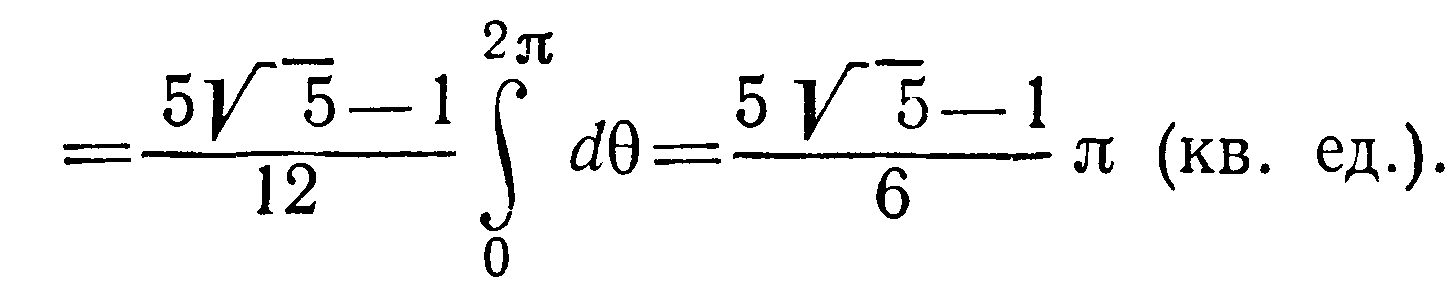
Задачи

36 . Найти площадь части поверхности

вырезанной цилиндром

37. Найти площадь части сферы

вырезанной цилиндром

38. Найти площадь той части плоскости z=
x:, которая заключена
внутри цилиндра

39. Найти площадь части поверхности
цилиндра z = x²,
вырезанной плоскостями

40. Вычислить площадь поверхности конуса

расположенной внутри цилиндра

41. Вычислить площадь поверхности цилиндра

расположенной внутри цилиндра

42. Найти площадь части поверхности

вырезанной плоскостями

Индивидуальные задания

Тройной интеграл

Пусть функция f (х, у, z)
определена в ограниченной замкнутой
пространственной области Т. Разобьем
область Т произвольным образом на п
элементарных областей T₁
Т₂, …, Т_n с
диаметрами d₁ d₂,
…, dn и объемами ∆V₁,
∆V_{2, ….,}∆Vn.
В каждой элементарной области возьмем
произвольную точку P_k
(ξ₁, ξ₂, … , ξ_n
) и умножим значение функции в точке Р_k
на объем этой области.

Интегральной суммой для функции f
(х, у, z) по области Т
называется сумма вида

Предел интегральной суммы при стремлении
к нулю наибольшего из диаметров всех
элементарных областей ∆Vk
называется тройным интегралом от функции
f (х, у, z) по
области Т и обозначается следующим
образом:

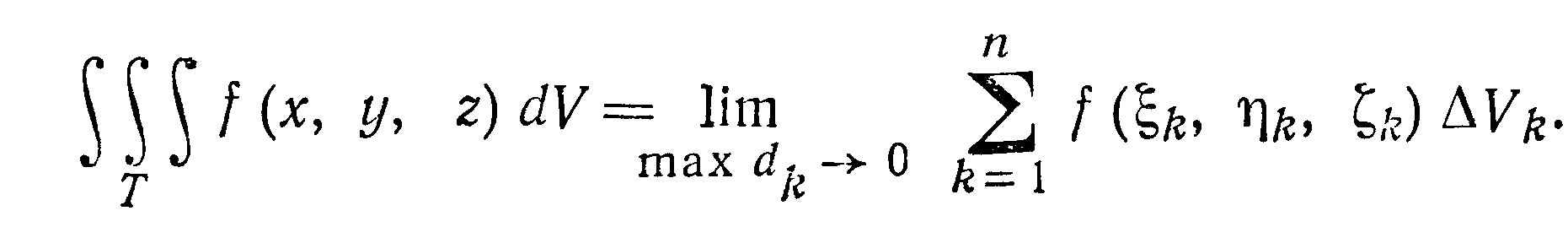
Конечный предел такого вида может
существовать только для ограниченной

функции.

Если f (х, у, z)
> 0 в области Т, то тройной интеграл

представляет собой массу тела, занимающего
область Т и имеющего переменную плотность
γ = f(x, у, z)
(физическое истолкование тройного
интеграла).

Основные свойства тройных интегралов
аналогичны свойствам двойных интегралов.

В декартовых координатах тройной
интеграл обычно записывают в виде

Пусть область интегрирования Т
определяется неравенствами x₁≤
x≤ x_2, y₁≤
y ≤ y_2,
z₁≤ z
≤ z_2, где y₁(x),
y₂(x),
z₁(x,y),
z₂ (x,y)
непрерывные функции. Тогда тройной
интеграл от функции f (х,
у, z), распространенный на область Т,
вычисляется по формуле

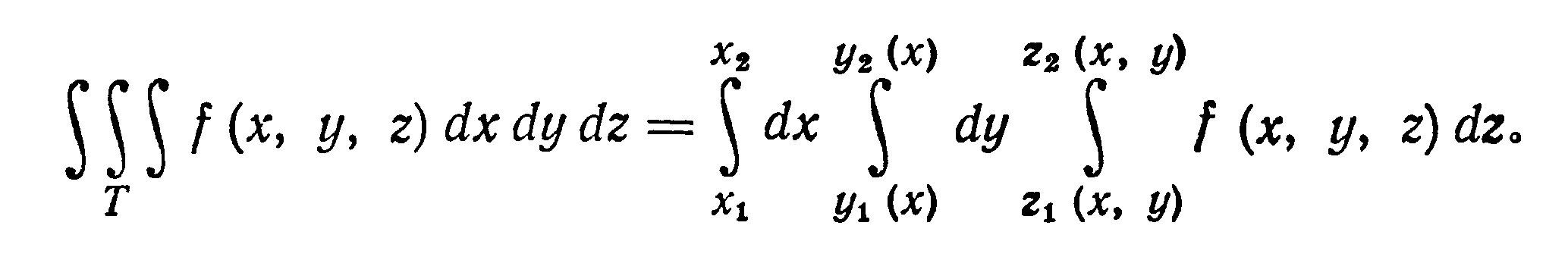
Если при вычислении тройного интеграла
требуется перейти от переменных х, у, z
к новым переменным и, v, w, связанным с х,
у, z соотношениями х = х(u,
v, w), y = y(u, v, w), z = z (u, v, w), где
функции х(и, v, w), y(u,v, w) z (u, v, w), непрерывные
вместе со своими частными производными
первого порядка, устанавливают взаимно
однозначное и в обе стороны непрерывное
соответствие между точками области Т
пространства Oxyz и точками некоторой
области Т’ пространства Ouvw и якобиан J
в области Т’ не обращается в нуль

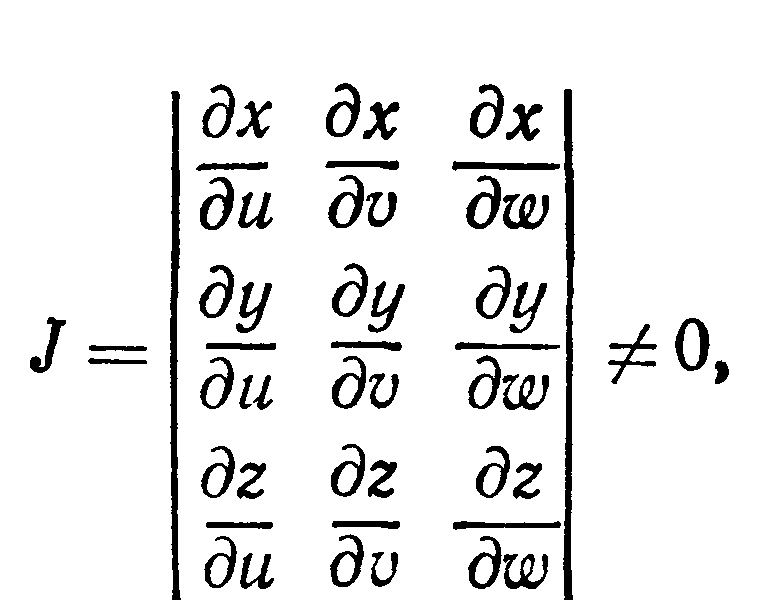
то пользуются формулой

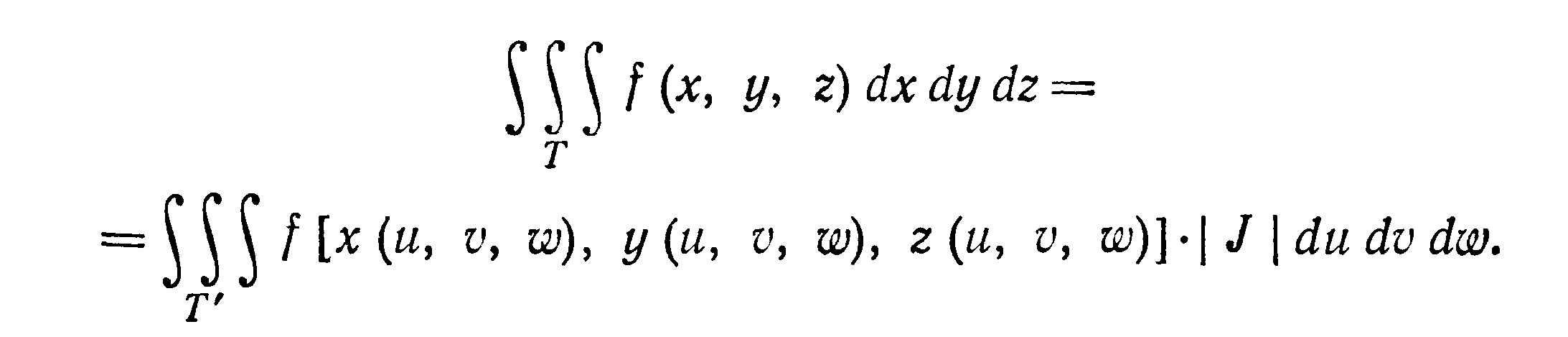
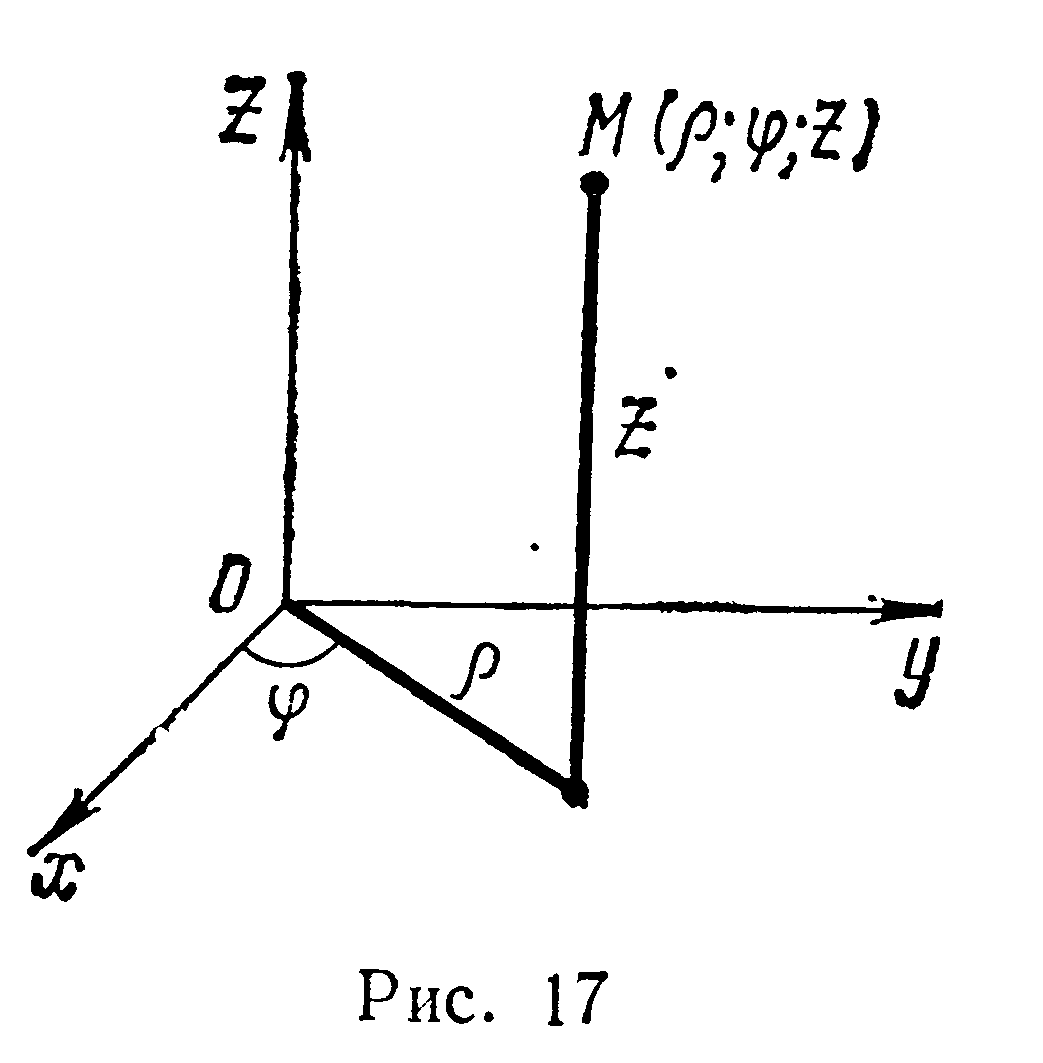
В частности, при переходе от декартовых
координат х, у, z к
цилиндрическим координатам ρ,φ , z
(рис. 17), связанным с х, у, z
соотношениями

якобиан преобразования J = ρ
и формула преобразования тройного
интеграла

к цилиндрическим координатам имеет вид

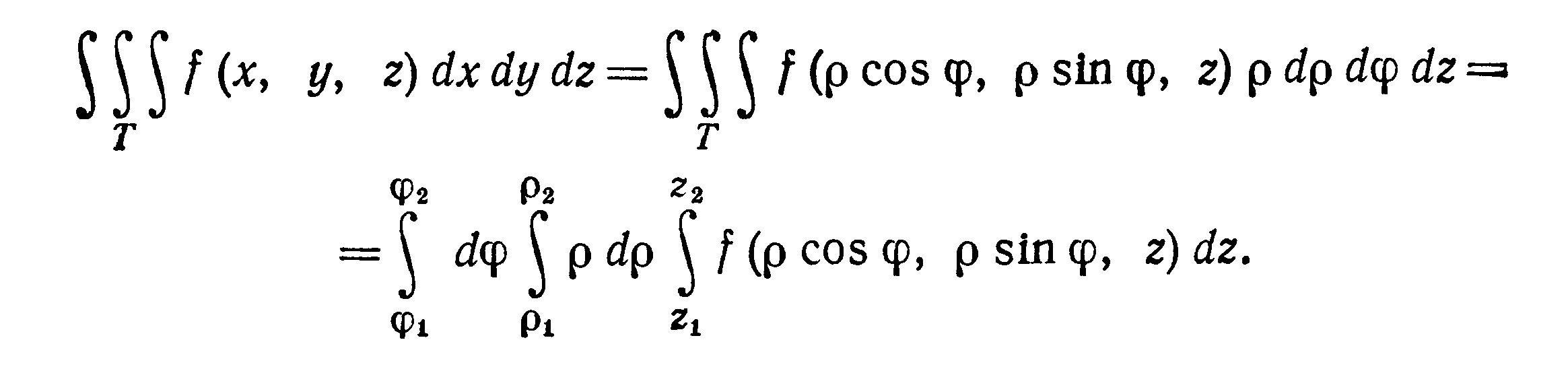
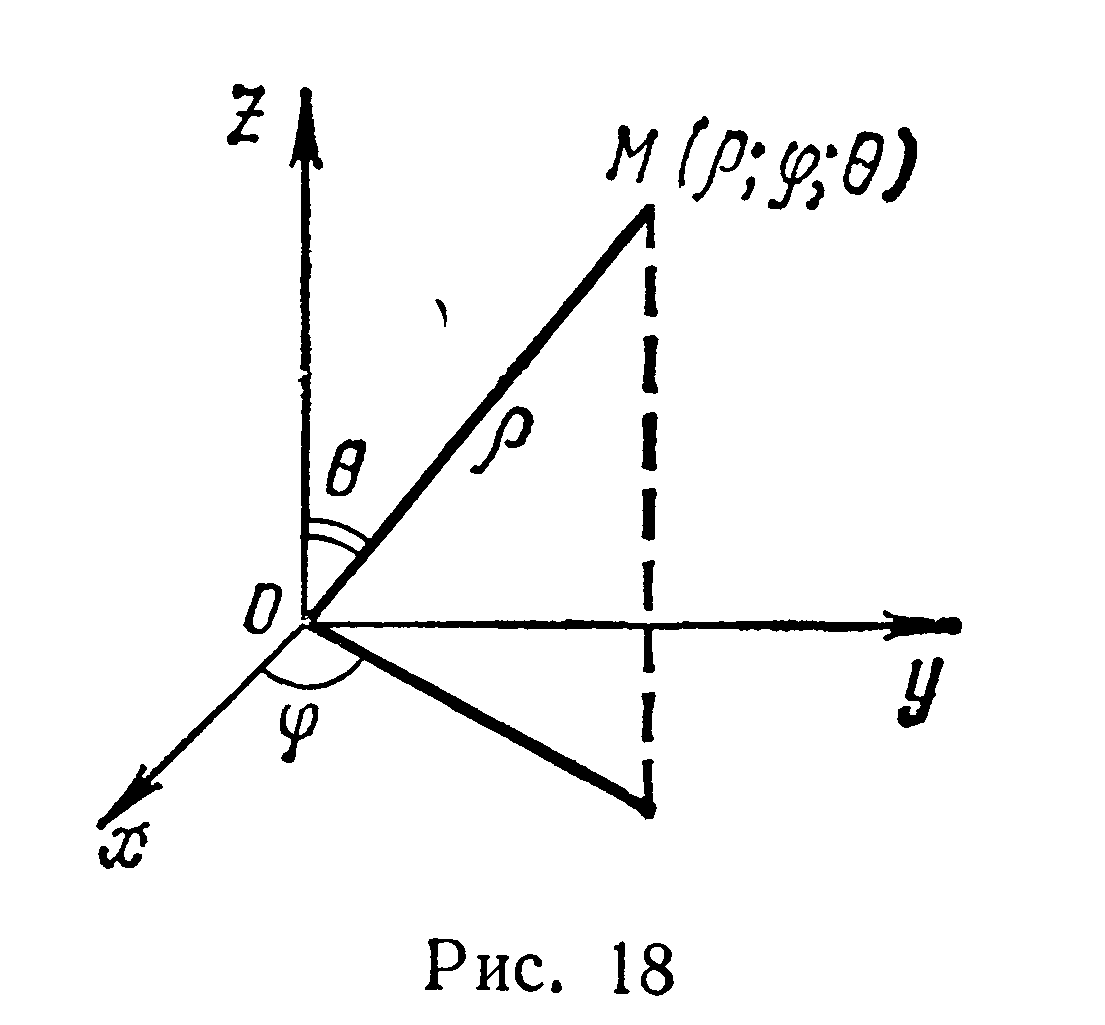
При переходе от декартовых координат
х, у, z к сферическим координатам ρ,φ,θ
(рис. 18), связанным с х, у, z соотношениями

якобиан преобразования J
= ρ² sinθ, и формула
преобразования тройного интеграла к
сферическим координатам имеет вид

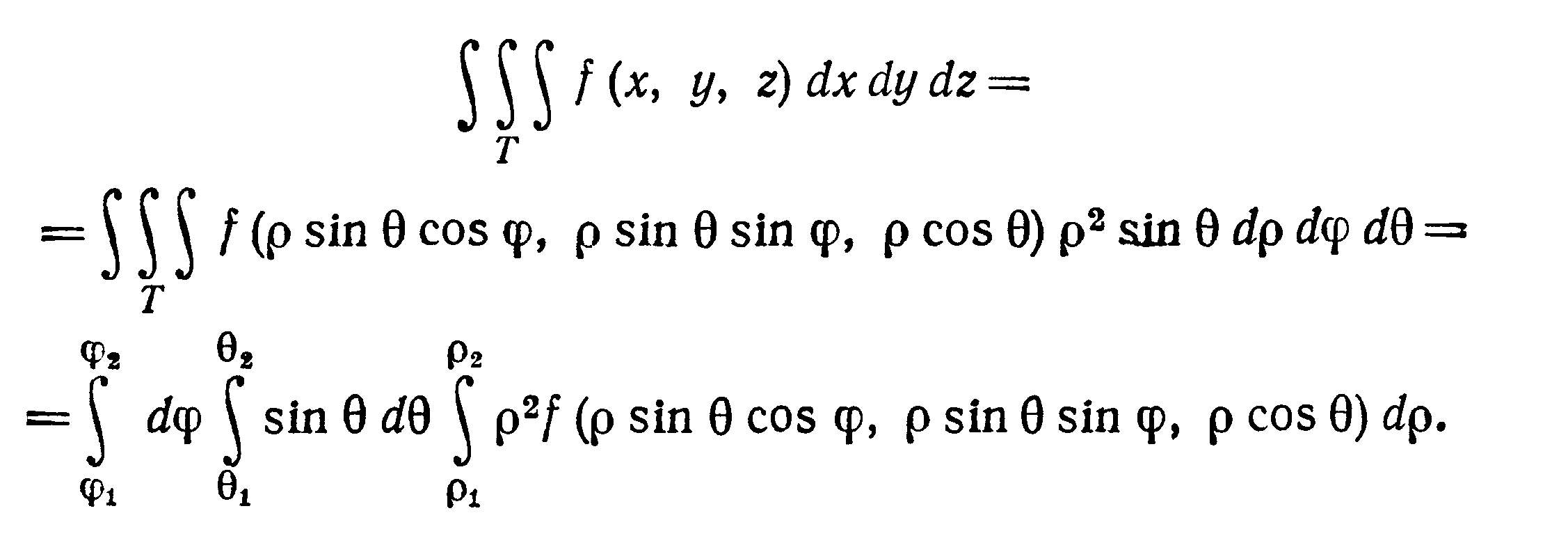
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #