- Главная
- Справочники
- Справочник по математике для начальной школы
- Основы геометрии
- Площадь фигуры
В этом разделе мы познакомимся с новым математическим понятием: с площадью фигуры.
Площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией
Ты знаешь другие понятия, которые тоже называют словом ПЛОЩАДЬ.
Например, площадь в городе – это чаще всего красивое место с клумбами, фонтаном и памятниками.
Посевная площадь – это участок земли, предназначенный для сельскохозяйственных целей.
Сравнение площадей фигур
При сравнении площади фигур, мы узнаём, больше или меньше места занимает данная фигура на плоскости.
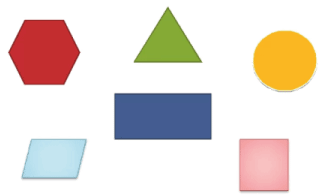
Например, сравним площади двух фигур: треугольника и круга.
Мы видим, что площадь треугольника больше площади круга. Это видно на глаз, то есть первый способ сравнения площадей фигур: на глазок.
Сравнение площадей способом наложения
Иногда на глаз трудно определить, площадь какой фигуры больше. Давай сравним площади двух треугольников:
Совместим фигуры так, чтобы одна фигура полностью поместилась в другой.
Мы видим, что синий треугольник поместился в красном треугольнике, значит, площадь красного треугольника больше, чем площадь синего треугольника.
Сравнение площадей заданной меркой
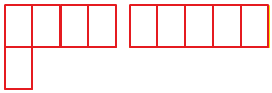
Иногда нельзя определить, площадь какой фигуры больше способом наложения. Давай сравним площади двух фигур:
В таком случае измерять площади фигур будем заданной меркой, а потом сравним их.
Например, меркой может быть вот такой прямоугольник :
В первой фигуре поместилось 5 мерок, во второй фигуре поместилось 5 таких же мерок. Значит, площади фигур равны.
Единицы площади
В математике измерять площади фигур математики всего мира договорились одинаковыми мерками.
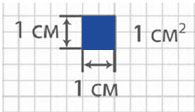
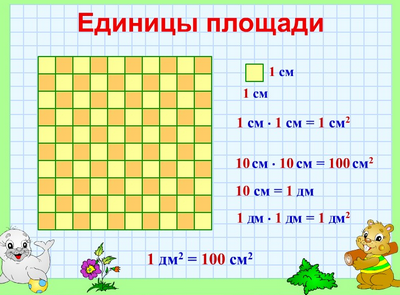
Квадратный сантиметр
Квадрат, сторона которого 1 см – это единица площади – квадратный сантиметр: см²
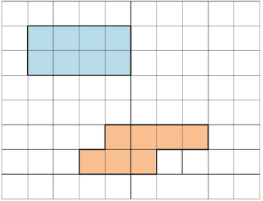
Определим площадь данных фигур:
В синей фигуре 8 см², а в красной фигуре – 7 см².
8 > 7, значит, 8 см² > 7 см² а это значит, что площадь синей фигуры больше, чем площадь красной фигуры.
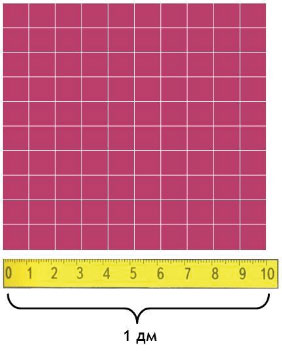
Квадратный дециметр
Квадрат, сторона которого 1 дм – это единица площади – квадратный дециметр: дм²
Вычислим, сколько квадратных сантиметров содержится в 1 квадратном дециметре:
1 дм² = ? см²
Сторона такого квадрата равна 10 см, а площадь квадрата равна произведению его сторон, то есть
10 • 10 = 100 см²
Значит, 1 дм² = 100 см²
Квадратный метр
Квадрат, сторона которого 1 м – это единица площади – квадратный метр: м²
Этой единицей мы пользуемся, когда хотим узнать площадь комнаты, класса, школьного двора или бабушкиного сада.
1 м² = 100 дм²
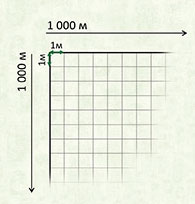
Квадратный километр
Квадрат, сторона которого 1 км – это единица площади – квадратный километр: км²
Этой единицей мы пользуемся, когда хотим узнать площадь города или страны. Например, площадь России составляет более семнадцати миллионов квадратных километров.
1 км² = 1000000 м²
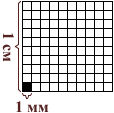
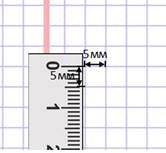
Квадратный миллиметр
Квадрат, сторона которого 1 мм – это единица площади – квадратный миллиметр: мм²
Этой единицей мы пользуемся для измерения очень маленьких площадей.
1 см² = 100 мм²
Длина и ширина клеточки школьной тетради по математике – пять миллиметров, значит там пять рядов по пять квадратных миллиметров. 5 • 5 = 25, поэтому в одной клеточке двадцать пять квадратных миллиметров.
Для черчения и измерения фигур маленькой площади удобно использовать миллиметровую бумагу.
Ар
Ар – это площадь квадрата со стороной 10 м.
Слово “ар” при числах сокращённо записывают так:
1 а, 20 а, 97 а.
1 а2 = 100 м2, поэтому ар часто называют соткой.
Гектар
Гектар – это площадь квадрата со стороной 100 м.
Слово “гектар” при числах сокращённо записывают так:
1 га, 20 га, 530 га.
Чтобы перевести площадь из квадратных метров в гектары, необходимо число квадратных метров разделить на 10000.
Ар и гектар используются при измерении земельных участков.
Советуем посмотреть:
Площадь прямоугольника
Круг. Шар. Овал
Треугольники
Многоугольники
Угол. Виды углов
Обозначение геометрических фигур буквами
Периметр многоугольника
Окружность
Основы геометрии
Правило встречается в следующих упражнениях:
2 класс
Страница 43. Урок 17,
Петерсон, Учебник, часть 2
Страница 44. Урок 17,
Петерсон, Учебник, часть 2
Страница 65. Урок 26,
Петерсон, Учебник, часть 2
Страница 82. Урок 34,
Петерсон, Учебник, часть 2
Страница 88. Урок 37,
Петерсон, Учебник, часть 2
Страница 100. Урок 41,
Петерсон, Учебник, часть 2
Страница 49. Урок 17,
Петерсон, Учебник, часть 3
Страница 52. Урок 18,
Петерсон, Учебник, часть 3
Страница 56. Урок 20,
Петерсон, Учебник, часть 3
Страница 90. Урок 35,
Петерсон, Учебник, часть 3
3 класс
Страница 59,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 105,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 54,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 85. Урок 31,
Петерсон, Учебник, часть 1
Страница 94. Урок 35,
Петерсон, Учебник, часть 1
Страница 67. Урок 28,
Петерсон, Учебник, часть 2
Страница 88. Урок 38,
Петерсон, Учебник, часть 2
Страница 20. Урок 9,
Петерсон, Учебник, часть 3
Страница 37. Урок 17,
Петерсон, Учебник, часть 3
Страница 51. Урок 23,
Петерсон, Учебник, часть 3
4 класс
Страница 66,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 96,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 64,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 58. ПР 2. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 59. ПР 2. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 76,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 95,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 103,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 114,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 33,
Моро, Волкова, Рабочая тетрадь, часть 2
Математика, 3 класс
Урок №21. Площадь. Способы сравнения фигур по площади. Единица площади – квадратный сантиметр
Перечень вопросов, рассматриваемых в теме:
– что такое площадь фигуры?
– какие есть способы сравнения фигур по площади?
– что такое квадратный сантиметр?
Глоссарий по теме:
Площадь – внутренняя часть любой плоской геометрической фигуры.
Квадрат – это прямоугольник, у которого все стороны равны.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 56-59.
2. Рудницкая В. Н. Тесты по математике:3 класс. М.:Издательство «Экзамен», 2016 с. 38-43.
3. Волкова Е. В. ВПР. Математика 3 класс Практикум по выполнению типовых заданий. ФГОС. М.: Издательство «Экзамен», 2018, с. 36-53.
Теоретический материал для самостоятельного изучения
Сравним фигуры и расставим их в порядке убывания их площади.
Фигуры расположили в следующем порядке: 4, 2, 1, 6, 5, 3.
В математике говорят: площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией. Когда мы сравниваем площади фигур, мы выясняем, больше или меньше места занимает данная фигура на плоскости. Мы сравнивали эти фигуры способом, который называется «на глаз».
Сравним фигуры и выясним, площадь какой фигуры больше.
Способом сравнения на глаз, определить площадь какой фигуры невозможно.
Для этого существует способ сравнения: наложения.

Вывод: площадь прямоугольника больше площади круга.
Сравним две фигуры.
Изученными способами сравнить площади не получается. Есть еще один способ сравнения: подсчет количества одинаковых мерок.
Посчитаем количество мерок в фигурах: в синей фигуре содержится 6 мерок, в красной-5 мерок, следовательно, площадь синей фигуры больше площади красной, т. к. в синей фигуре 6 мерок-квадратов, а в красной – 5.
В математике мерка- квадрат. А квадрат со стороной 1 см называется квадратный сантиметр и обозначается см2..
Задания тренировочного модуля:
1.Выберите правильное высказывание:
Площадь фигуры – это…..
1. сумма длин всех сторон
2. внутренняя часть фигуры
Правильный ответ:
2. внутренняя часть фигуры
2. Выделите фигуры с одинаковой площадью.
Правильный ответ:
Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.
Площади равных фигур равны. Их периметры тоже равны.
Площадь квадрата
Запомните!
Для вычисления площади квадрата нужно умножить его длину на саму себя.
S = a · a
Пример:
SEKFM = EK · EK
SEKFM = 3 · 3 = 9 см2
Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:
S = a2
Площадь прямоугольника
Запомните!
Для вычисления площади прямоугольника нужно умножить его длину на ширину.
S = a · b
Пример:
SABCD = AB · BC
SABCD = 3 · 7 = 21 см2
Запомните!
Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.
Площадь сложных фигур
Запомните!
Площадь всей фигуры равна сумме площадей её частей.
Задача: найти площадь огородного участка.
Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.
Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.
SABCE = AB · BC
SEFKL = 10 · 3 = 30 м2
SCDEF = FC · CD
SCDEF = 7 · 5 = 35 м2
Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = SABCE + SEFKL
S = 30 + 35 = 65 м2
Ответ: S = 65 м2 — площадь огородного участка.
Свойство ниже может вам пригодиться при решении задач на площадь.
Запомните!
Диагональ прямоугольника делит прямоугольник на два равных треугольника.
Площадь любого из этих треугольников равна половине площади прямоугольника.
Рассмотрим прямоугольник:
АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников
ABC и

Вначале найдём площадь прямоугольника по формуле.
SABCD = AB · BC
SABCD = 5 · 4 = 20 см2
S
ABC = SABCD : 2
S
ABC = 20 : 2 = 10 см2
S
ABC =
S
ACD = 10 см2
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
3 декабря 2015 в 22:54
Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
как написать правильно площадь треугольника?
0
Спасибо
Ответить
9 декабря 2015 в 19:41
Ответ для Ирина Петренко
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
S(рисуешь мини треугольник) = ,,,,,
0
Спасибо
Ответить
Периметр данного многоугольника можно найти сложив длинны всех его сторон, но для начала придётся найти длинны двух сторон – АВ и АК:
АВ = CD + EK = 2 + 1 = 3 см
AK = BC + DE = 4 + 2 = 6 см
Теперь можно найти периметр всей фигуры:
Р = AB + BC + CD + DE + EK + AK = 3 + 4 + 2 + 2 + 1 + 6 = 18 см
Площадь же многоугольника можно найти, как минимум пятью способами ( правда не уверен, что в третьем классе уже умеют находить площадь трапеций по длинам оснований и высоте – в данном случае трапеции ABCD и ADEK ). Для того, чтобы проще описать способы решения я добавил на чертёж ещё три точки ( впрочем, для разных вариантов решения не все точки потребуются одновременно ).
Вот такой чертёжик у меня получился
Проще всего найти площадь этой фигуры так
S = S(ABEK) – S(CDEH) = AB * AK – CD * DE = 3 * 6 – 2 * 2 = 18 – 4 = 14 см²
Второй способ:
S = S(ABCG) + S(DEGK) = AB * BC + DE * EK = 3 * 4 + 2 * 1 = 12 + 2 = 14 см²
Третий способ:
S = S(BCDF) + S(AFEK) = BC * CD + AK * EK = 4 * 2 + 6 * 1 = 8 + 6 = 14 см²
Четвёртый способ:
S = S(BCDF) + S(AFDG) + S(DEKG) = BC * CD + AG * AF + DE * EK = 4 * 2 + 4 * 1 + 2 * 1 = 8 + 4 + 2 = 14 см²
Ну, и, наконец, пятый способ с трапециями ( извиняюсь, забыл провести на чертеже ещё и AD, впрочем в решении его величина не важна ):
S = S(ABCD) + S(ADEK) = BC * ( AB + CD )/2 + EK * ( DE + AK )/2 = 4 * ( 3 + 2 )/2 + 1 * ( 2 + 6 )/2 = 10 + 4 = 14 см²
Ответ: периметр многоугольника равен 18 см, а его площадь – 14 см²
Инфоурок
›
Начальные классы
›Презентации›Презентация по математике на тему :”Площадь фигуры” 3 класс Школа России
Скачать материал
без ожидания

Скачать материал
без ожидания




аудиоформат


- Сейчас обучается 115 человек из 46 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
ПЛОЩАДЬ.
ЕДИНИЦЫ ПЛОЩАДИ. -
2 слайд
Организационный момент
На уроке наши глаза внимательно
Смотрят и все … (видят).
Уши внимательно слушают
И всё …(слышат).
Голова хорошо … (думает0. -
3 слайд
26 октября.
Классная работа.. -
4 слайд
5 ∙ 2 = 10 14 : 2 = 7
9 ∙ 1 = 9 16 : 8 = 2
4 ∙ 5 = 20 25 : 5 = 5
Найди число
Какие числа закрыты -
5 слайд
Сколько будет, если взять 3 раза по 4?
Сколько будет: 6 троек?
Сколько раз по 5 входит в число 10?
3 умножить на 4.Арифметический диктант
-
6 слайд
6 х
3
8
6
4
7
9
Устный счёт
18, 48, 36, 24, 42, 54. -
7 слайд
Устный счёт
8, 5, 6, 9, 3, 7.
: 7
56
35
42
63
21
49 -
8 слайд
Тема :
Площадь
фигуры
?
? -
9 слайд
Главная площадь нашей страны
-
10 слайд
ПЛОЩАДЬ –
Владимир Даль
это величина, которая указывает, сколько места занимает фигура на плоскости. -
11 слайд
Какие меры длины знаете?
мм
СМ
ДМ
М
КМ -
12 слайд
Способы измерения площади…
? -
-
14 слайд
РАБОТА С
ГЕОМЕТРИЧЕСКИМ
МАТЕРИАЛОМ
КАК МОЖНО СРАВНИТЬ ЭТИ ФИГУРЫ?
Они имеют РАВНЫЕ
ПЛОЩАДИ -
15 слайд
СРАВНИТЕ ФИГУРЫ
Что можно сказать про площадь треугольника?
ПЛОЩАДЬ
треугольника меньше ПЛОЩАДИ
квадрата -
16 слайд
СРАВНИТЕ ФИГУРЫ
Можно ли на «глаз» или наложением определить, площадь какой фигуры больше?
20
18
Площадь больше
Площадь меньше -
17 слайд
СПРАВКА
При разных мерках получается разный результат измерения.
Поэтому сравнивать, складывать и вычитать величины можно только тогда, когда они выражены одинаковыми мерками. -
18 слайд
Площадь фигуры – величина, показывающая сколько места занимает фигура на плоскости.
-
19 слайд
S – площадь фигуры
169 клеток
175 клеток
S1 < S2 -
-
21 слайд
НАЧЕРТИ
ПРЯМОУГОЛЬНИК СО СТОРОНАМИ
3 СМ И 5 СМ
ПОСЧИТАЙ СКОЛЬКО КЛЕТОЧЕК В НЕМ ПОМЕСТИЛОСЬ. -
22 слайд
ПРОВЕРЬ
60
s
= 60 клеток -
23 слайд
МЕРКА
3 + 3 + 3 + 3 = 12
11 + 11 + 11 + 11 = 44
8 + 8 + 8 + 8 = 32 -
24 слайд
В качестве общепринятой единицы измерения площадей (мерок) используют
квадрат со стороной 1 см.Это измерение называют:
квадратный сантиметр – 1 см².ЕДИНИЦЫ ИЗМЕРЕНИЯ
-
25 слайд
Какие единицы измерения площади вы знаете?
Что значит квадратный сантиметр?
1 см 2
Найдите площади данных фигур.
2.
1.
3. -
26 слайд
Это прямоугольник со сторонами 6 см и 4 см.
Разделим его на квадратные сантиметры
Ширина прямоугольника
Длина прямоугольника
Сколько полос с квадратами получилось?
Сколько квадратов в каждой полосе?
Как узнать, сколько всего квадратов?
Что такое 6?
Что такое 4?
Сделайте вывод, как найти площадь прямоугольника?
4
6
S = a · b
a
b
а-длина, b-ширина -
-
28 слайд
Площадь прямоугольника
1.Чтобы найти площадь прямоугольника, измеряют его длину и ширину (в одинаковых единицах) и находят произведение полученных чисел.2.Чтобы найти площадь прямоугольника, надо его длину умножить на ширину.
-
29 слайд
Найдите площадь прямоугольника
4 см
6 см
S=a•b
S = 6 • 4 = 24 см² -
30 слайд
Электронная физминутка для глаз «Крошка Енот»
-
-
-
33 слайд
Какими единицами пользуются
для измерения площади ?
А для чего это надо знать?
Что такое площадь фигуры?
Площадь фигуры – величина, показывающая сколько места занимает фигура на плоскости.
Какие способы сравнения площадей вы сегодня узнали? -
34 слайд
a
b
S
=
a
.
b
формула нахождения
площади прямоугольника -
35 слайд
Домашнее задание
С. 46,
Спасибо, ребята!
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 252 093 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
Рейтинг:
4 из 5
- 14.12.2015
- 27487
- 3747
Рейтинг:
4 из 5
- 14.12.2015
- 8615
- 685
Рейтинг:
4 из 5
- 14.12.2015
- 5224
- 59
- 14.12.2015
- 1612
- 10
- 14.12.2015
- 744
- 0
- 14.12.2015
- 2465
- 5
- 14.12.2015
- 1135
- 1
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Роль педагога в реализации концепции патриотического воспитания школьников в образовательном процессе в свете ФГОС»
-
Курс повышения квалификации «Использование мини-проектов в школьном: начальном, основном и среднем общем и среднем профессиональном естественнонаучном образовании в условиях реализации ФГОС»
-
Курс повышения квалификации «Воспитание и социализация учащихся в условиях реализации ФГОС»
-
Курс повышения квалификации «Система образовательной организации в начальном общем образовании в условиях реализации ФГОС»
-
Курс профессиональной переподготовки «Организация инклюзивного обучения в сфере образования»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Применение современных педагогических технологий в образовательном процессе в условиях реализации ФГОС»
-
Курс повышения квалификации «Продуктивность учебной деятельности младших школьников общеобразовательного учреждения в рамках реализации ФГОС НОО»
-
Курс повышения квалификации «Видеотехнологии и мультипликация в начальной школе»
-
Курс повышения квалификации «Проективные методики в начальной школе в соответствии с ФГОС»
-
Курс повышения квалификации «Методы интерактивного обучения»
-
Курс повышения квалификации «Новые методы и технологии преподавания в начальной школе по ФГОС»
-
Курс повышения квалификации «Современные тенденции цифровизации образования»
-
Курс повышения квалификации «Формирование и развитие ключевых компетенций школьников в интересах устойчивого развития региона»
-
Курс профессиональной переподготовки «Музыка: теория и методика преподавания в сфере начального общего, основного общего, среднего общего образования»
-
Скачать материал (медленно)
Настоящий материал опубликован пользователем Письменская Ольга Михайловна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 8 лет и 6 месяцев
- Подписчики: 1
- Всего просмотров: 217427
-
Всего материалов:
33