Площадь треугольника
У геометрической фигуры — треугольника — 3 стороны и 3 вершины. Треугольник получается, если три точки, которые не лежат на одной прямой, соединить отрезками.
Для названия треугольника используются большие латинские буквы, при этом соблюдается последовательность вершин, но начинать название можно с любой вершины.
Иногда используют знак Δ.
В зависимости от величин углов треугольника выделяют:
- остроугольные треугольники (все углы острые, как на рисунке выше);
- прямоугольные треугольники (один угол прямой — ∡P=90°);
- тупоугольные треугольники (один угол тупой — ∡M).
Виды треугольников
Площадь треугольника
Прямоугольный треугольник легко представить как половину прямоугольника.
Если площадь прямоугольника равна произведению длин сторон, то для определения площади треугольника необходимо это произведение разделить на 2.
Допустим, RP = a, TP = b;
SRPT=(ab)/2.
Если треугольник не имеет прямого угла, можно построить два прямоугольника, как показано на рисунке.
Допустим, MA=BD=NC = h, AC = a.
SABC=SABD+SCBD=h⋅AD/2+h⋅DC/2=h⋅AC/2=h⋅a/2.
Как видно, достаточно в треугольнике от одной вершины провести отрезок под прямым углом к противолежащей стороне и использовать длины отрезка для определения площади треугольника.
Отрезок называют высотой треугольника.
Свойства треугольника
- длина любой стороны треугольника меньше суммы длин двух остальных сторон, но больше разницы длин двух остальных сторон;
- высота треугольника образует прямой угол со стороной, к которой проведена;
- площадь треугольника равна половине произведения длины высоты треугольника и длины стороны, к которой проведена высота SABC=a⋅h/2.
Пример. Можно ли построить треугольник из отрезков с длинами: 3 см, 7 см, 4 см?
Пример. Можно ли построить треугольник из отрезков с длинами: 16 см, 32 см, 18 см?
Пример. Можно ли построить треугольник из отрезков с длинами: 1 см, 3 см, 7 см ?
Пример. Одна сторона, которая образует прямой угол прямоугольного треугольника ABD, равна 4 см, другая сторона, которая образует прямой угол, в 2 раза меньше. Определи площадь треугольника.
Одна сторона, которая образует прямой угол прямоугольного треугольника ABD, равна 12 см, другая сторона, которая образует прямой угол, в 3 раза меньше.
Определи площадь треугольника.
Рассчитай площадь треугольника ABC, если дана площадь клетки — 1 м 2 .
Поэтому площадь можно рассчитать следующим образом:
Известно, что периметр равностороннего треугольника — 21 см. Определи периметр данного четырёхугольника, который состоит из равносторонних треугольников.
Значит, одна сторона треугольника равна 7 см.
Периметр данного четырёхугольника состоит из 4 таких сторон, значит, равен 28 см.
Дан равносторонний треугольник. 2 раза сделано следующее:
1. на всех сторонах отмечены и соединены серединные точки.
2. На сторонах внутреннего треугольника опять отмечены и соединены серединные точки.
Треугольник, который образовался на этот раз, закрашен розовым цветом.
1. Сколько маленьких треугольников необходимо для перекрытия данного треугольника?
2. Чему равна площадь большого треугольника, если площадь розового треугольника равна 4 м²?
3. Сколько маленьких треугольников получится, если повторить эти действия (построить такую конструкцию) 4 раза?
Если повторить эти действия (построить такую конструкцию) 4 раза, то общее число маленьких треугольников будет равняться 256.
4. Сколько маленьких треугольников получится, если повторить эти действия (построить такую конструкцию) 3 раза?
Если повторить эти действия (построить такую конструкцию) 3 раза, то общее число маленьких треугольников будет равняться 64.
Определи площадь данных фигур, если площадь одной клетки равна 6 см2.
1)
Сколько клеток образует площадь фигуры? Чему равна площадь фигуры?
Сколько клеток образует площадь фигуры? Чему равна площадь фигуры?
Подумай, как построены данные фигуры, и определи, сколько клеток будет у следующих двух фигур, если их построить по той же закономерности.
Как найти площадь треугольника – все способы от самых простых до самых сложных
Зависит от того, какой треугольник.

Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.
Если треугольник прямоугольный
То есть один из его углов равен 90 градусам.
Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.

Если он равнобедренный
То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.

Если он равносторонний
То есть все три стороны равны. Ваши действия такие:
- Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
- Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
- Поделите все на 4.

Если известна сторона и высота
Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.

Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.
Если известны две стороны и градус угла между ними
Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:

Если известны длины трех сторон
- Найдите периметр. Для этого сложите все три стороны.
- Найдите полупериметр – разделите периметр на два. Запомните значение.
- Отнимите от полупериметра длину первой стороны. Запомните.
- Отнимите от полупериметра длину второй стороны. Тоже запомните.
- Отнимите от полупериметра длину третьей стороны. И ее запомните.
- Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
- Найдите квадратный корень.

Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.
Если известны три стороны и радиус описанной окружности
Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.

Если известны три стороны и радиус вписанной окружности
Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.
Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.

Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.
Как найти площадь треугольника

О чем эта статья:
8 класс, 9 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Площадь — это численная характеристика, которая дает нам информацию о размере части плоскости, ограниченной замкнутой геометрической фигурой.
Если значения заданы в разных единицах измерения длины, мы не сможем узнать, какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Формула площади треугольника
Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.
Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.
Научиться быстро щелкать задачки на нахождение площади треугольника помогут курсы по математике от Skysmart!
Общая формула
1. Площадь треугольника через основание и высоту
, где — основание, — высота.
2. Площадь треугольника через две стороны и угол между ними
, где , — стороны, — угол между ними.
3. Площадь треугольника через описанную окружность и стороны
, где , , — стороны, — радиус описанной окружности.
4. Площадь треугольника через вписанную окружность и стороны
, где , , — стороны, — радиус вписанной окружности.
Если учитывать, что — это способ поиска полупериметра, то формулу можно записать следующим образом:
5. Площадь треугольника по стороне и двум прилежащим углам
, где — сторона, и — прилежащие углы.
6. Формула Герона для вычисления площади треугольника
Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.
, где , , — стороны, — полупериметр, который можно найти по формуле:
Для прямоугольного треугольника
Площадь треугольника с углом 90° по двум сторонам
Площадь треугольника по гипотенузе и острому углу
, где — гипотенуза, — любой из прилегающих острых углов.
Гипотенузой принято называть сторону, которая лежит напротив прямого угла.
Площадь прямоугольного треугольника по катету и прилежащему углу
, где — катет, — прилежащий угол.
Катетом принято называть одну из двух сторон, образующих прямой угол.
Площадь треугольника через гипотенузу и радиус вписанной окружности
, где — гипотенуза, — радиус вписанной окружности.
Площадь треугольника по отрезкам, на которые делит вписанная окружность его гипотенузу
, где , — части гипотенузы.
Площадь прямоугольного треугольника по формуле Герона
, где , — катеты, — полупериметр, который можно найти по формуле:
Для равнобедренного треугольника
Вычисление площади через основание и высоту
, где — основание, — высота, проведенная к основанию.
Поиск площади через боковые стороны и угол между ними
, где — боковая сторона, — угол между боковыми сторонами.
Площадь равностороннего треугольника через радиус описанной окружности
, где — радиус описанной окружности.
Площадь равностороннего треугольника через радиус вписанной окружности
, где — радиус вписанной окружности.
Площадь равностороннего треугольника через сторону
Площадь равностороннего треугольника через высоту
Таблица формул нахождения площади треугольника
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу, использовать как закладку в тетрадке или учебнике и обращаться к ней по необходимости.
[spoiler title=”источники:”]
http://vsvoemdome.ru/obrazovanie/kak-nayti-ploschad-treugolnika
http://skysmart.ru/articles/mathematic/ploshad-treugolnika
[/spoiler]
- Главная
- Справочники
- Справочник по математике для начальной школы
- Основы геометрии
- Площадь фигуры
В этом разделе мы познакомимся с новым математическим понятием: с площадью фигуры.
Площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией
Ты знаешь другие понятия, которые тоже называют словом ПЛОЩАДЬ.
Например, площадь в городе – это чаще всего красивое место с клумбами, фонтаном и памятниками.

Посевная площадь – это участок земли, предназначенный для сельскохозяйственных целей.

Сравнение площадей фигур
При сравнении площади фигур, мы узнаём, больше или меньше места занимает данная фигура на плоскости.
Например, сравним площади двух фигур: треугольника и круга.

Мы видим, что площадь треугольника больше площади круга. Это видно на глаз, то есть первый способ сравнения площадей фигур: на глазок.
Сравнение площадей способом наложения
Иногда на глаз трудно определить, площадь какой фигуры больше. Давай сравним площади двух треугольников:

Совместим фигуры так, чтобы одна фигура полностью поместилась в другой.

Мы видим, что синий треугольник поместился в красном треугольнике, значит, площадь красного треугольника больше, чем площадь синего треугольника.
Сравнение площадей заданной меркой
Иногда нельзя определить, площадь какой фигуры больше способом наложения. Давай сравним площади двух фигур:

В таком случае измерять площади фигур будем заданной меркой, а потом сравним их.
Например, меркой может быть вот такой прямоугольник : 
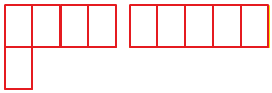
В первой фигуре поместилось 5 мерок, во второй фигуре поместилось 5 таких же мерок. Значит, площади фигур равны.
Единицы площади
В математике измерять площади фигур математики всего мира договорились одинаковыми мерками.
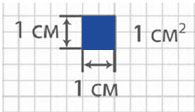
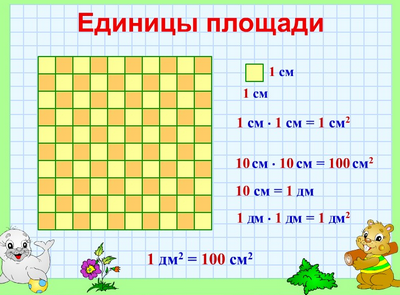
Квадратный сантиметр
Квадрат, сторона которого 1 см – это единица площади – квадратный сантиметр: см²
Определим площадь данных фигур:
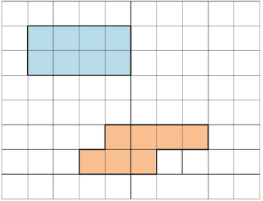
В синей фигуре 8 см², а в красной фигуре – 7 см².
8 > 7, значит, 8 см² > 7 см² а это значит, что площадь синей фигуры больше, чем площадь красной фигуры.
Квадратный дециметр
Квадрат, сторона которого 1 дм – это единица площади – квадратный дециметр: дм²
Вычислим, сколько квадратных сантиметров содержится в 1 квадратном дециметре:
1 дм² = ? см²
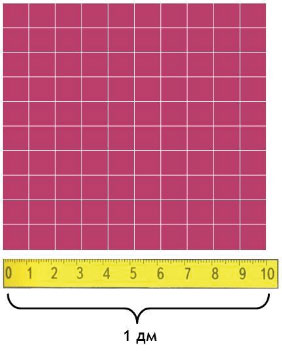
Сторона такого квадрата равна 10 см, а площадь квадрата равна произведению его сторон, то есть
10 • 10 = 100 см²
Значит, 1 дм² = 100 см²
Квадратный метр
Квадрат, сторона которого 1 м – это единица площади – квадратный метр: м²
Этой единицей мы пользуемся, когда хотим узнать площадь комнаты, класса, школьного двора или бабушкиного сада.
1 м² = 100 дм²
Квадратный километр
Квадрат, сторона которого 1 км – это единица площади – квадратный километр: км²
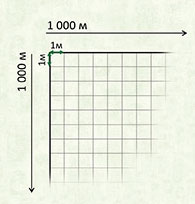
Этой единицей мы пользуемся, когда хотим узнать площадь города или страны. Например, площадь России составляет более семнадцати миллионов квадратных километров.
1 км² = 1000000 м²
Квадратный миллиметр
Квадрат, сторона которого 1 мм – это единица площади – квадратный миллиметр: мм²
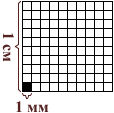
Этой единицей мы пользуемся для измерения очень маленьких площадей.
1 см² = 100 мм²
Длина и ширина клеточки школьной тетради по математике – пять миллиметров, значит там пять рядов по пять квадратных миллиметров. 5 • 5 = 25, поэтому в одной клеточке двадцать пять квадратных миллиметров.
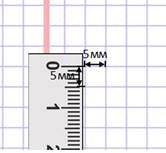
Для черчения и измерения фигур маленькой площади удобно использовать миллиметровую бумагу.
Ар
Ар – это площадь квадрата со стороной 10 м.
Слово “ар” при числах сокращённо записывают так:
1 а, 20 а, 97 а.
1 а2 = 100 м2, поэтому ар часто называют соткой.
Гектар
Гектар – это площадь квадрата со стороной 100 м.
Слово “гектар” при числах сокращённо записывают так:
1 га, 20 га, 530 га.
Чтобы перевести площадь из квадратных метров в гектары, необходимо число квадратных метров разделить на 10000.
Ар и гектар используются при измерении земельных участков.
Советуем посмотреть:
Площадь прямоугольника
Круг. Шар. Овал
Треугольники
Многоугольники
Угол. Виды углов
Обозначение геометрических фигур буквами
Периметр многоугольника
Окружность
Основы геометрии
Правило встречается в следующих упражнениях:
2 класс
Страница 44. Урок 17,
Петерсон, Учебник, часть 2
Страница 45. Урок 17,
Петерсон, Учебник, часть 2
Страница 50. Урок 19,
Петерсон, Учебник, часть 2
Страница 68. Урок 27,
Петерсон, Учебник, часть 2
Страница 81. Урок 33,
Петерсон, Учебник, часть 2
Страница 91. Урок 38,
Петерсон, Учебник, часть 2
Страница 100. Урок 41,
Петерсон, Учебник, часть 2
Страница 33. Урок 11,
Петерсон, Учебник, часть 3
Страница 49. Урок 17,
Петерсон, Учебник, часть 3
Страница 52. Урок 18,
Петерсон, Учебник, часть 3
3 класс
Страница 57,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 35,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 46,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 54,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 95,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 41,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 44,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 22. Урок 7,
Петерсон, Учебник, часть 1
Страница 87. Урок 32,
Петерсон, Учебник, часть 1
Страница 91. Урок 40,
Петерсон, Учебник, часть 2
4 класс
Страница 72,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 94,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 46,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 33. Тест 1. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 53. Тест 2. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 17,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 62,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 114,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 78,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 32. Урок 11,
Петерсон, Учебник, часть 1
У геометрической фигуры — треугольника — 3 стороны и 3 вершины. Треугольник получается, если три точки, которые не лежат на одной прямой, соединить отрезками.
Для названия треугольника используются большие латинские буквы, при этом соблюдается последовательность вершин, но начинать название можно с любой вершины.
Иногда используют знак Δ.
![]()
В зависимости от величин углов треугольника выделяют:
- остроугольные треугольники (все углы острые, как на рисунке выше);
- прямоугольные треугольники (один угол прямой — ∡P=90°);
- тупоугольные треугольники (один угол тупой — ∡M).
![]()
Площадь треугольника
Прямоугольный треугольник легко представить как половину прямоугольника.
![]()
Если площадь прямоугольника равна произведению длин сторон, то для определения площади треугольника необходимо это произведение разделить на 2.
Допустим, RP = a, TP = b;
SRPT=(ab)/2.
Если треугольник не имеет прямого угла, можно построить два прямоугольника, как показано на рисунке.
![]()
Допустим, MA=BD=NC = h, AC = a.
SABC=SABD+SCBD=h⋅AD/2+h⋅DC/2=h⋅AC/2=h⋅a/2.
Как видно, достаточно в треугольнике от одной вершины провести отрезок под прямым углом к противолежащей стороне и использовать длины отрезка для определения площади треугольника.
Отрезок называют высотой треугольника.
![]()
Свойства треугольника
- длина любой стороны треугольника меньше суммы длин двух остальных сторон, но больше разницы длин двух остальных сторон;
- высота треугольника образует прямой угол со стороной, к которой проведена;
- площадь треугольника равна половине произведения длины высоты треугольника и длины стороны, к которой проведена высота SABC=a⋅h/2.
Пример. Можно ли построить треугольник из отрезков с длинами: 3 см, 7 см, 4 см?
Пример. Можно ли построить треугольник из отрезков с длинами: 16 см, 32 см, 18 см?
Пример. Можно ли построить треугольник из отрезков с длинами: 1 см, 3 см, 7 см ?
Одна сторона, которая образует прямой угол прямоугольного треугольника ABD, равна 12 см, другая сторона, которая образует прямой угол, в 3 раза меньше.
Определи площадь треугольника.
Рассчитай площадь треугольника ABC, если дана площадь клетки — 1 м2.
![]()
Известно, что периметр равностороннего треугольника — 21 см. Определи периметр данного четырёхугольника, который состоит из равносторонних треугольников.
Дан равносторонний треугольник. 2 раза сделано следующее:
1. на всех сторонах отмечены и соединены серединные точки.
2. На сторонах внутреннего треугольника опять отмечены и соединены серединные точки.
Треугольник, который образовался на этот раз, закрашен розовым цветом.
![]()
1. Сколько маленьких треугольников необходимо для перекрытия данного треугольника?
2. Чему равна площадь большого треугольника, если площадь розового треугольника равна 4 м²?
3. Сколько маленьких треугольников получится, если повторить эти действия (построить такую конструкцию) 4 раза?
4. Сколько маленьких треугольников получится, если повторить эти действия (построить такую конструкцию) 3 раза?
Определи площадь данных фигур, если площадь одной клетки равна 6 см2.
1)
![]()
Сколько клеток образует площадь фигуры? Чему равна площадь фигуры?
![]()
Сколько клеток образует площадь фигуры? Чему равна площадь фигуры?
Подумай, как построены данные фигуры, и определи, сколько клеток будет у следующих двух фигур, если их построить по той же закономерности.
Лучший ответ
NIИ
Мастер
(2228)
13 лет назад
Высоту умножить на сторону, к которой она проведена
Остальные ответы
Вахит Шавалиев
Высший разум
(762740)
13 лет назад
Найденную площадь прямоугоьника КАРИНАКЕННЕ разделить по полам, получится площадь треугольника.
Элеонора Полякова
Искусственный Интеллект
(111844)
13 лет назад
Площадь тр-ка равна половине произведения основания на высоту.
Ксения Буланкина
Мастер
(1308)
13 лет назад
умножить основание на высоту и делить на2
valesya
Знаток
(256)
13 лет назад
можно по формуле герона если тока стороны даны
ксюша симонова
Ученик
(92)
13 лет назад
Sтреуг. =1/2высоту на сторону (к кот проведена)
Слава Зайцев
Ученик
(164)
6 лет назад
П
Светлана Соколова
Ученик
(207)
6 лет назад
именно
Федорова Наталия
Знаток
(276)
5 лет назад
Вы что, это же 3тий класс, я думаю так: Sтреугольника= Sпрямоугольника ÷2
Цель: формирование навыка построения геометрических фигур; расширение знаний о фигурах; развитие исследовательских умений в открытии нового, воспитание любви к предмету, бережного отношения к своему здоровью
Оборудование: счетные палочки, фигуры прямоугольных треугольников, карточки с заданием, ТСО, эмблемы настроения (по 3 шт)
Ход урока
1. Организационный момент
Слайд 1
Учитель:
Прозвенел звонок и смолк,
Он позвал нас на урок.
Вы проверьте все ль в порядке,
Ручка, карандаш, тетрадка.
Что-то новое узнаем,
Повторим, поразмышляем.
– Ребята, поделитесь, пожалуйста, со мной своим настроением (дети поднимают эмблемы настроения)
– А для работы, как вы думаете, какой лучше настрой выбрать?
– Для создания рабочей обстановки, давайте выполним упражнения для восстановления дыхания
- Задуть одну свечу, пять свечей
Давайте создадим хороший эмоциональный настрой: улыбнитесь, пожмите друг другу руку, пожелайте удачи.
2. Актуализация знаний, определение темы и цели урока
– Итак, у нас урок геометрии. Внимательно посмотрите на слайд и скажите, какая фигура лишняя и почему?
Слайд 2
(Лишняя фигура – треугольник, так как остальные – четырехугольники)
– Значит, с какими фигурами мы будем работать на уроке? (с треугольниками). Что вы знаете о треугольнике? (ответы детей)
– Определите тему урока (Нахождение площади прямоугольного треугольника). Чему должны научиться сегодня на уроке?
Слайд 3
– Правильно, сегодня на уроке мы постараемся найти способ нахождения площади прямоугольного треугольника, повторим виды треугольников, будем учиться выполнять чертежи.
III. А сейчас геометрическая разминка, но прежде выполним массаж точек мозга, упражнение для концентрации внимания «Горизонтальная восьмерка»
- Упражнение «Горизонтальная восьмерка»
Вытяните перед собой правую руку на уровне глаз, пальцы сожмите в кулак, оставив средний и указательный пальцы вытянутыми. Нарисуйте в воздухе горизонтальную восьмерку как можно большого размера. Рисовать начинайте с центра и следите глазами за кончиками пальцев, не поворачивая головы. Затем подключите язык, т.е. рисуйте восьмерку не только пальцами, но и синхронно языком, хорошо выдвинутым изо рта, продолжая следить глазами за движением пальцев.
– Посмотрите на данные линии, назовите их. Что вы знаете о луче, отрезке?
Слайд 4
(Луч – прямая линия, у которой есть начало; отрезок – часть прямой, у которой есть начало и конец)
Задание1: Сколько линий можно провести через одну точку? Через две точки?
Задание 2. Длина отрезка 3 см. Чему равен второй отрезок, если он длиннее первого в два раза? (6 см); если он длиннее на 2 см? (5 см)
Задание 3. Сложите из семи палочек три треугольника.
Задание 4. Найдите и исправьте ошибки
Слайд 5
4. Работа по теме
1. Повторение о треугольниках
Учитель. Какие виды треугольников вы знаете? Дайте каждому из них определение.
Слайд 6
(равнобедренный, равносторонний, прямоугольный)
Учитель. Рассмотрите и определите, какие из треугольников являются прямоугольными. Как мы определим? (с помощью чертежного угольника)
Слайд 7
Упражнения: массаж кончиков пальцев
Задание в тетради:
– Начертите прямоугольный треугольник. Какие виды работ мы можем с ним произвести?
(Обозначить буквами, найти длины сторон, найти периметр этого треугольника, определить виды углов).
– Может ли в прямоугольном треугольнике быть два прямых угла?
– Как найти площадь этого треугольника? (разбить его на квадратные см)
– Кто еще, какие предлагает варианты? (ответы детей)
– Площадь, каких фигур мы находили на прошлом уроке? (прямоугольника, квадрата)
Слайд 8
2. Открытие нового
– Используя знания нахождения площади прямоугольника, мы сегодня найдем способ нахождения площади прямоугольного треугольника.
– Сложите из треугольников, которые у вас есть, прямоугольник. Одинаковые ли треугольники вы использовали? Сколько треугольников составляют ваш прямоугольник? (два одинаковых прямоугольных треугольника)
– Можем ли мы найти площадь этого прямоугольника? Кто догадался, как мы можем найти площадь прямоугольного треугольника? (длину сторон, составляющих прямой угол умножить и разделить на да)
– Почему разделить на два? (ответы детей)
3. Работа в тетради
– Начертите прямоугольный треугольник со сторонами 4см, 2 см.
– Чему будет равна площадь треугольника? (4х2:2=2 кв см)
– Как мы нашли площадь треугольника? (нашли площадь прямоугольника, разделили на два)
– Можем ли записать формулу нахождения площади прямоугольного треугольника?
Слайд 9
4. Работа в парах (взаимопроверка)
Задание на закрепление: (карточки)
Начертите прямоугольный треугольник, 5 см, 4 см.
Найдите его площадь. (10 кв см)
5. Итог урока:
– Достигли ли мы цели урока? Научились ли находить площадь прямоугольного треугольника? Что понравилось на уроке?
6. Рефлексия.
– Оцените свое участие на уроке с помощью эмблем.
– Всем спасибо за урок.
