В данной публикации мы рассмотрим, как можно найти площадь поверхности куба и разберем примеры решения задач для закрепления материала.
-
Формула вычисления площади куба
- 1. Через длину ребра
- 2. Через длину диагонали грани
-
Примеры задач
Формула вычисления площади куба
1. Через длину ребра
Площадь (S) поверхности куба равна произведению числа 6 на длину его ребра в квадрате.
S = 6 ⋅ a2

Данная формула получена следующим образом:
- Куб – это правильная геометрическая фигура, все грани которого являются равными квадратами с длиной стороны a (одновременно является ребром куба).
- Площадь каждой грани считается так: S = a ⋅ a = a2.
- Всего у куба 6 граней, а значит, площадь его поверхности равняется шести площадям одной грани: S = 6 ⋅ a2.
2. Через длину диагонали грани
Сторона любой грани куба (ребро) может быть рассчитана через длину ее диагонали по формуле: a=d/√2.

Это значит, что вычислить площадь поверхности фигуры можно так:
S = 6 ⋅ (d/√2)2
Примеры задач
Задание 1
Найдите площадь поверхности куба, если длина его ребра составляет 12 см.
Решение:
Используем первую формулу выше и получаем:
S = 6 ⋅ (12 см)2 = 864 см2.
Задание 2
Площадь поверхности куба равняется 294 см2. Вычислите длину его ребра.
Решение:
Примем ребро куба за a. Из формулы расчета площади следует:![]()
Задание 3
Вычислите площадь поверхности куба, если диагональ его грани равняется 5 см.
Решение:
Воспользуемся формулой, в которой задействована длина диагонали:
S = 6 ⋅ (5 см : √2)2 = 75 см2.
Данный материал содержит геометрические фигуры с измерениями. Приведённые измерения являются приблизительными и могут не совпадать с измерениями в реальной жизни.
Периметр геометрической фигуры
Периметр геометрической фигуры — это сумма всех её сторон. Чтобы вычислить периметр, нужно измерить каждую сторону и сложить результаты измерений.
Вычислим периметр следующей фигуры:
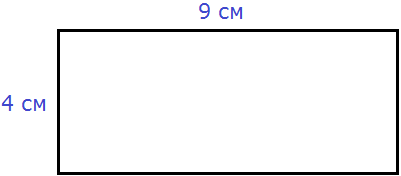
Это прямоугольник. Детальнее мы поговорим об этой фигуре позже. Сейчас просто вычислим периметр этого прямоугольника. Длина его равна 9 см, а ширина 4 см.
У прямоугольника противоположные стороны равны. Это видно на рисунке. Если длина равна 9 см, а ширина равна 4 см, то противоположные стороны будут равны 9 см и 4 см соответственно:
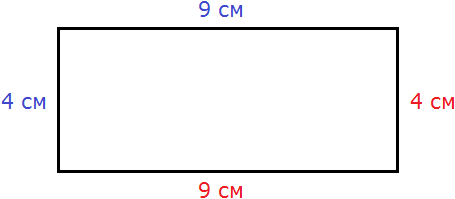
Найдём периметр. Для этого сложим все стороны. Складывать их можно в любом порядке, поскольку от перестановки мест слагаемых сумма не меняется. Периметр часто обозначается заглавной латинской буквой P (англ. perimeters). Тогда получим:
P = 9 см + 4 см + 9 см + 4 см = 26 см.
Поскольку у прямоугольника противоположные стороны равны, нахождение периметра записывают короче — складывают длину и ширину, и умножают её на 2, что будет означать «повторить длину и ширину два раза»
P = 2 × (9 + 4) = 18 + 8 = 26 см.
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, найдём периметр квадрата со стороной 5 см. Фразу «со стороной 5 см» нужно понимать как «длина каждой стороны квадрата равна 5 см»
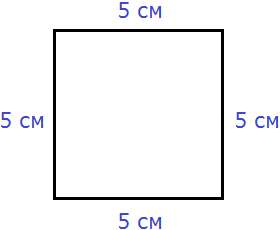
Чтобы вычислить периметр, сложим все стороны:
P = 5 см + 5 см + 5 см + 5 см = 20 см
Но поскольку все стороны равны, вычисление периметра можно записать в виде произведения. Сторона квадрата равна 5 см, и таких сторон 4. Тогда эту сторону, равную 5 см нужно повторить 4 раза
P = 5 см × 4 = 20 см
Площадь геометрической фигуры
Площадь геометрической фигуры — это число, которое характеризует размер данной фигуры.
Следует уточнить, что речь в данном случае идёт о площади на плоскости. Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.
Площадь измеряется в квадратных единицах. Под квадратными единицами подразумевают квадраты, стороны которых равны единице. Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.
Измерить площадь какой-нибудь фигуры означает выяснить сколько квадратных единиц содержится в данной фигуре.
Например, площадь следующего прямоугольника равна трём квадратным сантиметрам:

Это потому что в данном прямоугольнике содержится три квадрата, каждый из которых имеет сторону, равную одному сантиметру:
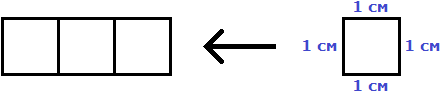
Справа представлен квадрат со стороной 1 см (он в данном случае является квадратной единицей). Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза.
Следующий прямоугольник имеет площадь, равную шести квадратным сантиметрам:

Это потому что в данном прямоугольнике содержится шесть квадратов, каждый из которых имеет сторону, равную одному сантиметру:
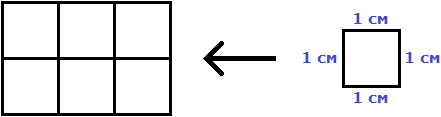
Допустим, потребовалось измерить площадь следующей комнаты:

Определимся в каких квадратах будем измерять площадь. В данном случае площадь удобно измерить в квадратных метрах:
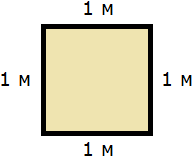
Итак, наша задача состоит в том, чтобы определить сколько таких квадратов со стороной 1 м содержится в исходной комнате. Заполним этим квадратом всю комнату:

Видим, что квадратный метр содержится в комнате 12 раз. Значит, площадь комнаты составляет 12 квадратных метров.
Площадь прямоугольника
В предыдущем примере мы вычислили площадь комнаты, последовательно проверив сколько раз в ней содержится квадрат, сторона которого равна одному метру. Площадь составила 12 квадратных метров.
Комната представляла собой прямоугольник. Площадь прямоугольника можно вычислить перемножив его длину и ширину.
Чтобы вычислить площадь прямоугольника, нужно перемножить его длину и ширину.
Вернёмся к предыдущему примеру. Допустим, мы измерили длину комнаты рулеткой и оказалось, что длина составила 4 метра:
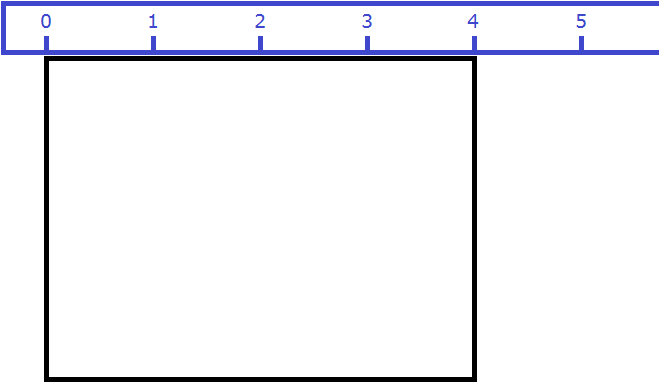
Теперь измерим ширину. Пусть она составила 3 метра:
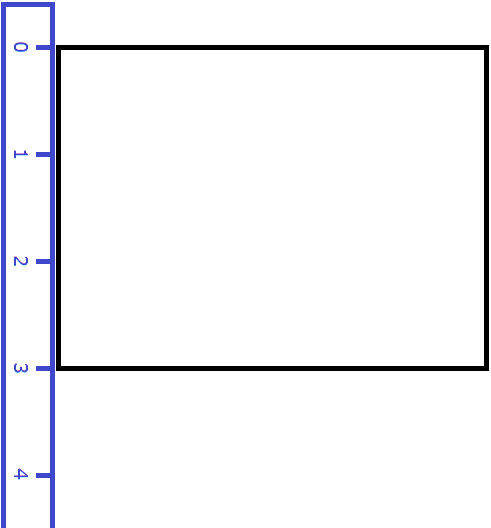
Умножим длину (4 м) на ширину (3 м).
4 × 3 = 12
Как и в прошлый раз получаем двенадцать квадратных метров. Это объясняется тем, что измерив длину, мы тем самым узнаём сколько раз можно уложить в эту длину квадрат со стороной, равной одному метру. Уложим четыре квадрата в эту длину:
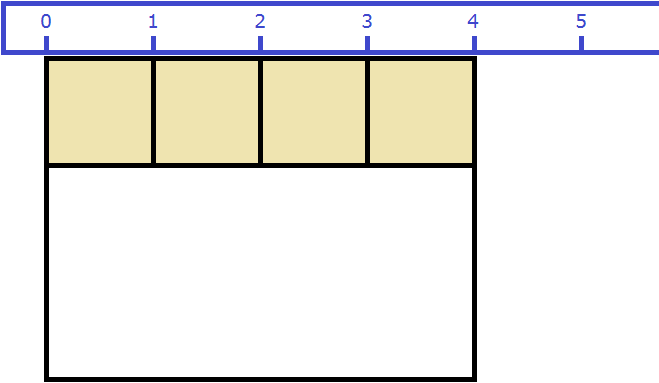
Затем мы определяем сколько раз можно повторить эту длину с уложенными квадратами. Это мы узнаём, измерив ширину прямоугольника:
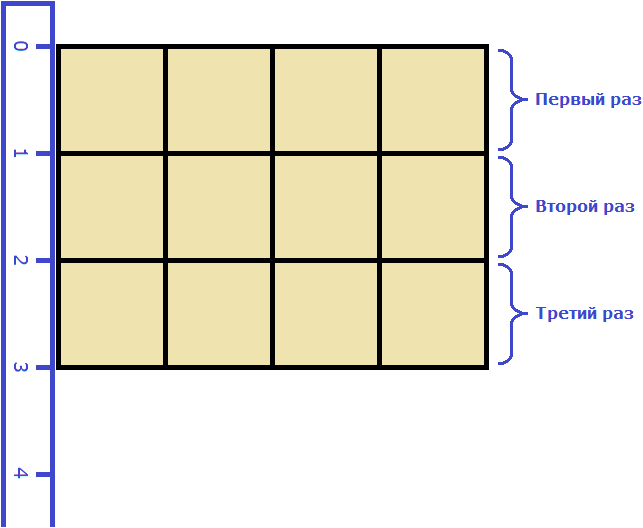
Площадь квадрата
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см
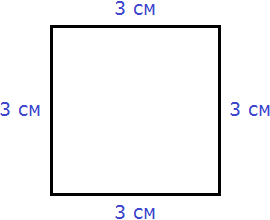
Площадь квадрата вычисляется таким же образом, как и площадь прямоугольника — длину умножают на ширину.
Вычислим площадь квадрата со стороной 3 см. Умножим длину 3 см на ширину 3 см
3 × 3 = 9
В данном случае требовалось узнать сколько квадратов со стороной 1 см содержится в исходном квадрате. В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:
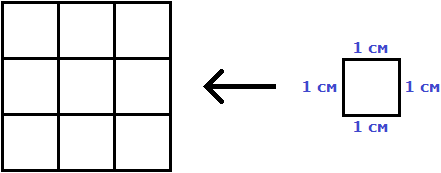
Умножив длину на ширину, мы получили выражение 3 × 3, а это есть произведение двух одинаковых множителей, каждый из которых равен 3. Иными словами выражение 3 × 3 представляет собой вторую степень числа 3. А значит процесс вычисления площади квадрата можно записать в виде степени 32.
Поэтому вторую степень числа называют квадратом числа. При вычислении второй степени числа a, человек тем самым находит площадь квадрата со стороной a. Операцию возведения числа во вторую степень по другому называют возведением в квадрат.
Обозначения
Площадь обозначается заглавной латинской буквой S (англ. Square — квадрат). Тогда площадь квадрата со стороной a см будет вычисляться по следующему правилу
S = a2
где a — длина стороны квадрата. Вторая степень указывает на то, что происходит перемножение двух одинаковых сомножителей, а именно длины и ширины. Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.
Если задача состоит в том, чтобы определить сколько квадратов стороной 1 см содержится в исходном квадрате, то в качестве единиц измерения площади нужно указывать см2. Это обозначение заменяет словосочетание «квадратный сантиметр».
Например, вычислим площадь квадрат со стороной 2 см.
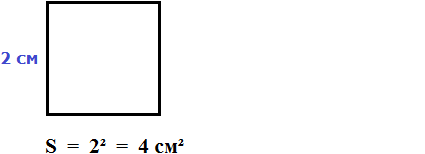
Значит, квадрат со стороной 2 см, имеет площадь, равную четырём квадратным сантиметрам:
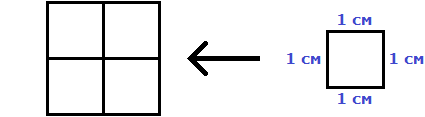
Если задача состоит в том, чтобы определить сколько квадратов со стороной 1 м содержится в исходном квадрате, то в качестве единиц измерения нужно указывать м2. Это обозначение заменяет словосочетание «квадратный метр».
Вычислим площадь квадрата со стороной 3 метра
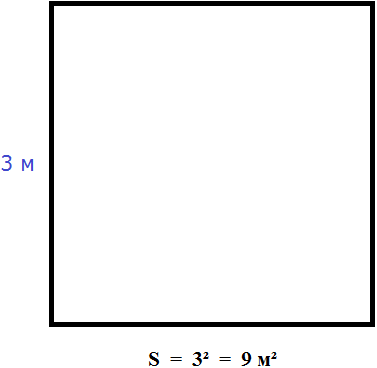
Значит, квадрат со стороной 3 м, имеет площадь равную девяти квадратным метрам:
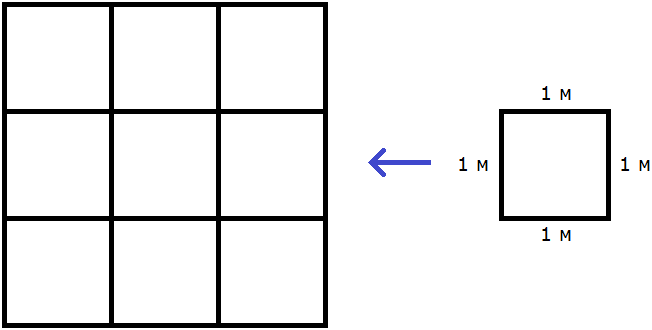
Аналогичные обозначения используются при вычислении площади прямоугольника. Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:
S = a × b
Как и в случае с квадратом, единицами измерения площади прямоугольника могут быть см2, м2, км2. Эти обозначения заменяют словосочетания «квадратный сантиметр», «квадратный метр», «квадратный километр» соответственно.
Например, вычислим площадь прямоугольника, длиной 6 см и шириной 3 см
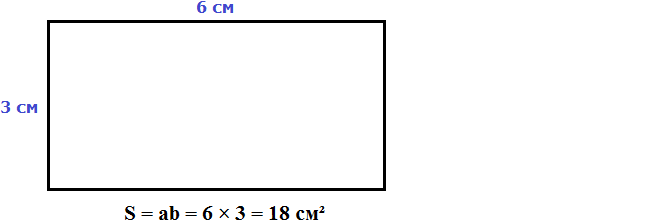
Значит, прямоугольник длиной 6 см и шириной 3 см имеет площадь, равную восемнадцати квадратным сантиметрам:
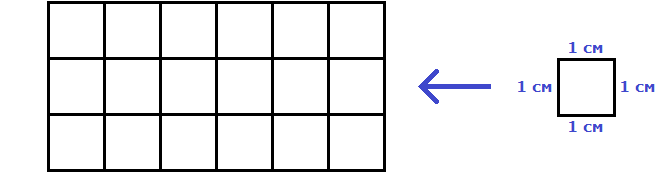
В качестве единицы измерения допускается использовать словосочетание «квадратных единиц». Например, запись S = 3 кв.ед означает, что площадь квадрата или прямоугольника равна трём квадратам, каждый из которых имеет единичную сторону (1 см, 1 м или 1 км).
Перевод единиц измерения площади
Единицы измерения площади можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
Пример 1. Выразить 1 квадратный метр в квадратных сантиметрах.
1 квадратный метр это квадрат со стороной 1 м. То есть все четыре стороны имеют длину, равную одному метру.
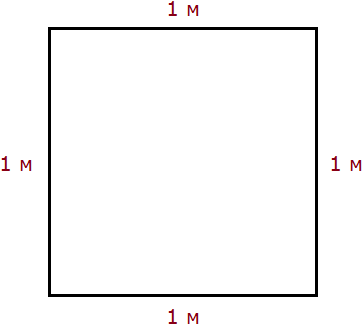
Но 1 м = 100 см. Тогда все четыре стороны тоже имеют длину, равную 100 см
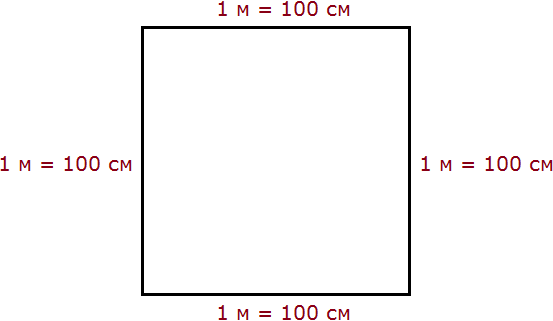
Вычислим новую площадь этого квадрата. Умножим длину 100 см на ширину 100 см или возведём в квадрат число 100
S = 1002 = 10 000 см2
Получается, что на один квадратный метр приходится десять тысяч квадратных сантиметров.
1 м2 = 10 000 см2
Это позволяет в будущем умножить любое количество квадратных метров на 10 000 и получить площадь, выраженную в квадратных сантиметрах.
Чтобы перевести квадратные метры в квадратные сантиметры, нужно количество квадратных метров умножить на 10 000.
А чтобы перевести квадратные сантиметры в квадратные метры, нужно наоборот количество квадратных сантиметров разделить на 10 000.
Например, переведём 100 000 см2 в квадратные метры. Рассуждать в этом случае можно так: «если 10 000 см2 это один квадратный метр, то сколько раз 100 000 см2 будут содержать по 10 000 см2»
100 000 см2 : 10 000 см2 = 10 м2
Другие единицы измерения можно переводить таким же образом. Например, переведём 2 км2 в квадратные метры.
Один квадратный километр это квадрат со стороной 1 км. То есть все четыре стороны имеют длину, равную одному километру. Но 1 км = 1000 м. Значит, все четыре стороны квадрата также равны 1000 м. Найдём новую площадь квадрата, выраженную в квадратных метрах. Для этого умножим длину 1000 м на ширину 1000 м или возведём в квадрат число 1000
S = 10002 = 1 000 000 м2
Получается, что на один квадратный километр приходится один миллион квадратных метров:
1 км2 = 1 000 000 м2
Это позволяет в будущем умножить любое количество квадратных километров на 1 000 000 и получить площадь, выраженную в квадратных метрах.
Чтобы перевести квадратные километры в квадратные метры, нужно количество квадратных километров умножить на 1 000 000.
Итак, вернёмся к нашей задаче. Требовалось перевести 2 км2 в квадратные метры. Умножим 2 км2 на 1 000 000
2 км2 × 1 000 000 = 2 000 000 м2
А чтобы перевести квадратные метры в квадратные километры, нужно наоборот количество квадратных метров разделить на 1 000 000.
Например, переведём 3 500 000 м2 в квадратные километры. Рассуждать в этом случае можно так: «если 1 000 000 м2 это один квадратный километр, то сколько раз 3 500 000 м2 будут содержать по 1 000 000 м2»
3 500 000 м2 : 1 000 000 м2 = 3,5 км2
Пример 2. Выразить 7 м2 в квадратных сантиметрах.
Умножим 7 м2 на 10 000
7 м2 = 7 м2 × 10 000 = 70 000 см2
Пример 3. Выразить 5 м2 13 см2 в квадратных сантиметрах.
5 м2 13 см2 = 5 м2 × 10 000 + 13 см2 = 50 013 см2
Пример 4. Выразить 550 000 см2 в квадратных метрах.
Узнаем сколько раз 550 000 см2 содержит по 10 000 см2. Для этого разделим 550 000 см2 на 10 000 см2
550 000 см2 : 10 000 см2 = 55 м2
Пример 5. Выразить 7 км2 в квадратных метрах.
Умножим 7 км2 на 1 000 000
7 км2 × 1 000 000 = 7 000 000 м2
Пример 6. Выразить 8 500 000 м2 в квадратных километрах.
Узнаем сколько раз 8 500 000 м2 содержит по 1 000 000 м2. Для этого разделим 8 500 000 м2 на 1 000 000 м2
8 500 000 м2 × 1 000 000 м2 = 8,5 км2
Единицы измерения площади земельных участков
Площади небольших земельных участков удобно измерять в квадратных метрах.
Площади более крупных земельных участков измеряются в арах и гектарах.
Ар (сокращённо: a) — это площадь равная ста квадратным метрам (100 м2). В виду частого распространения такой площади (100 м2) она стала использоваться, как отдельная единица измерения.
Например, если сказано что площадь какого-нибудь поля составляет 3 а, то нужно понимать, что это три квадрата площадью 100 м2 каждый, то есть:
3 а = 100 м2 × 3 = 300 м2
В народе ар часто называют соткой, поскольку ар равен квадрату, площадью 100 м2. Примеры:
1 сотка = 100 м2
2 сотки = 200 м2
10 соток = 1000 м2
Гектар (сокращенно: га) — это площадь, равная 10 000 м2. Например, если сказано что площадь какого-нибудь леса составляет 20 гектаров, то нужно понимать, что это двадцать квадратов площадью 10 000 м2 каждый, то есть:
20 га = 10 000 м2 × 20 = 200 000 м2
Прямоугольный параллелепипед и куб
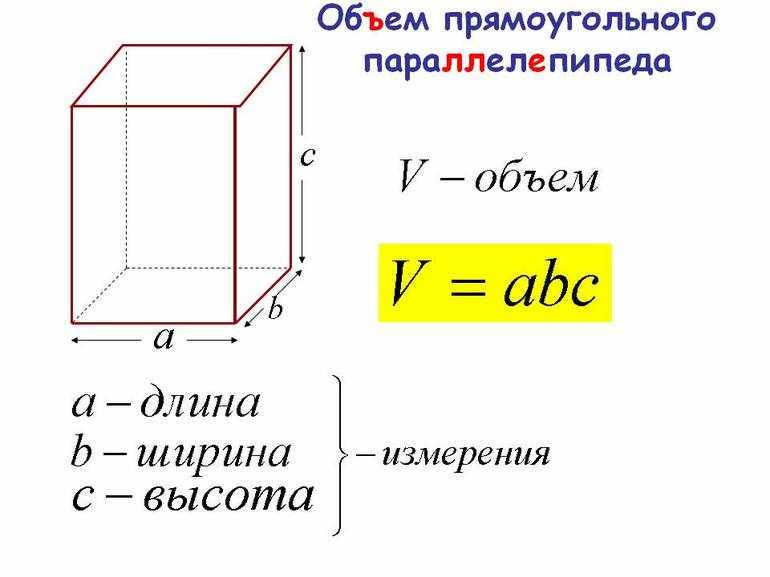
Прямоугольный параллелепипед — это геометрическая фигура, состоящая из грáней, рёбер и вершин. На рисунке показан прямоугольный параллелепипед:
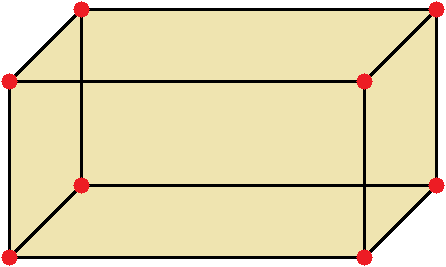
Желтым цветом показаны грáни параллелепипеда, чёрным цветом — рёбра, красным — вершины.
Прямоугольный параллелепипед обладает длиной, шириной и высотой. На рисунке показано где длина, ширина и высота:
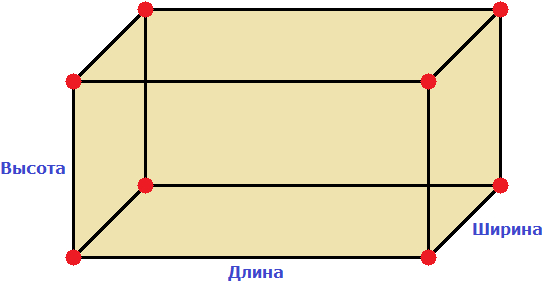
Параллелепипед, у которого длина, ширина и высота равны между собой, называется кубом. На рисунке показан куб:
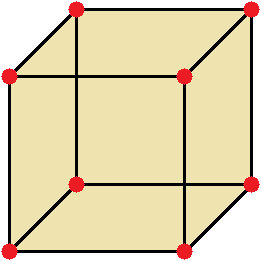
Объём геометрической фигуры
Объём геометрической фигуры — это число, которое характеризует вместимость данной фигуры.
Объём измеряется в кубических единицах. Под кубическими единицами подразумевают кубы длиной 1, шириной 1 и высотой 1. Например, 1 кубический сантиметр или 1 кубический метр.
Измерить объём какой-нибудь фигуры означает выяснить сколько кубических единиц вмещается в данную фигуру.
Например, объём следующего прямоугольного параллелепипеда равен двенадцати кубическим сантиметрам:
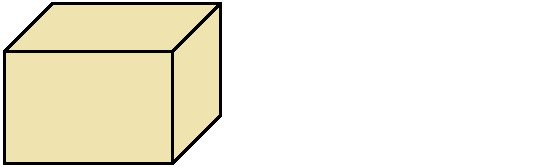
Это потому что в данный параллелепипед вмещается двенадцать кубов длиной 1 см, шириной 1 см и высотой 1 см:
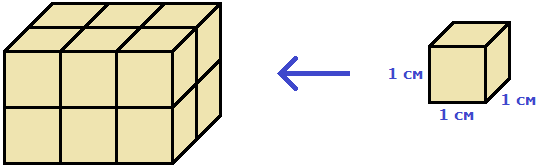
Объём обозначается заглавной латинской буквой V. Одна из единиц измерения объема это кубический сантиметр (см3). Тогда объём V рассмотренного нами параллелепипеда равен 12 см3
V = 12 см3
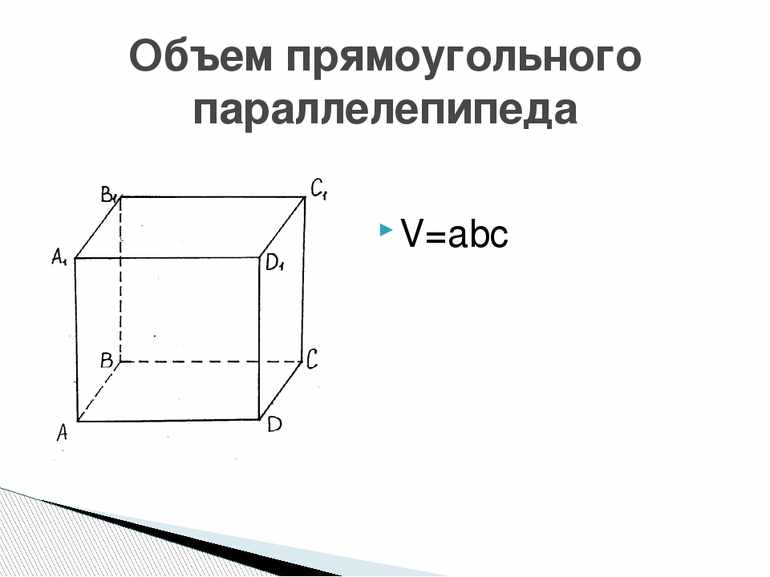
Объём любого параллелепипеда вычисляют следующим образом: перемножают его длину, ширину и высоту .
Объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
V = abc
где, a — длина, b — ширина, c — высота
Так, в предыдущем примере мы визуально определили, что объём параллелепипеда равен 12 см3. Но можно измерить длину, ширину и высоту данного параллелепипеда и перемножить результаты измерений. Мы получим тот же результат
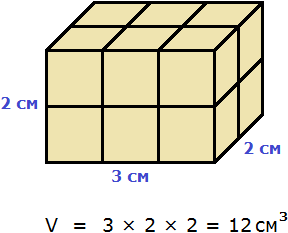
Объём куба вычисляется таким же образом, как и объём прямоугольного параллелепипеда — перемножают длину, ширину и высоту.
Например, вычислим объём куба, длина которого 3 см. У куба длина, ширина и высота равны между собой. Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:
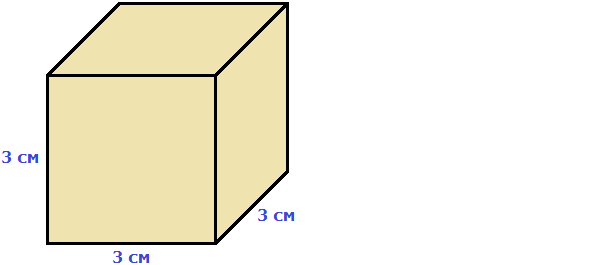
Перемножаем длину, ширину, высоту и получаем объём, равный двадцати семи кубическим сантиметрам:
V = 3 × 3 × 3 = 27 см³
Действительно, в исходный куб вмещается 27 кубиков длиной 1 см
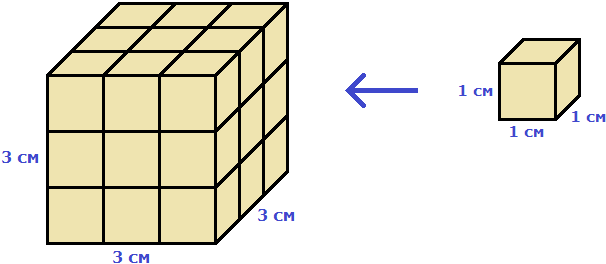
При вычислении объёма данного куба мы перемножили длину, ширину и высоту. Получилось произведение 3 × 3 × 3. Это есть произведение трёх сомножителей, каждый из которых равен 3. Иными словами, произведение 3 × 3 × 3 является третьей степенью числа 3 и может быть записано в виде 33.
V = 33 = 27 см3
Поэтому третью степень числа называют кубом числа. При вычислении третьей степени числа a, человек тем самым находит объём куба, длиной a. Операцию возведения числа в третью степень по другому называют возведением в куб.
Таким образом, объём куба вычисляется по следующему правилу:
V = a3
Где a — длина куба.
Кубический дециметр. Кубический метр
Не все объекты нашего мира удобно измерять в кубических сантиметрах. Например, объём комнаты или дома удобнее измерять в кубических метрах (м3). А объём бака, аквариума или холодильника удобнее измерять в кубических дециметрах (дм3).
Другое название одного кубического дециметра – один литр.
1 дм3 = 1 литр
Перевод единиц измерения объёма
Единицы измерения объёма можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
Пример 1. Выразить 1 кубический метр в кубических сантиметрах.
Один кубический метр это куб со стороной 1 м. Длина, ширина и высота этого куба равны одному метру.
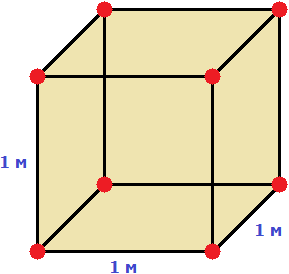
Но 1 м = 100 см. Значит, длина, ширина и высота тоже равны 100 см
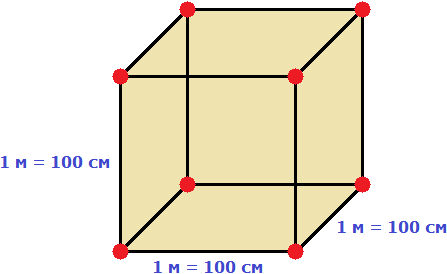
Вычислим новый объём куба, выраженный в кубических сантиметрах. Для этого перемножим его длину, ширину и высоту. Либо возведём число 100 в куб:
V = 1003 = 1 000 000 см3
Получается, что на один кубический метр приходится один миллион кубических сантиметров:
1 м3 = 1 000 000 см3
Это позволяет в будущем умножить любое количество кубических метров на 1 000 000 и получить объём, выраженный в кубических сантиметрах.
Чтобы перевести кубические метры в кубические сантиметры, нужно количество кубических метров умножить на 1 000 000.
А чтобы перевести кубические сантиметры в кубические метры, нужно наоборот количество кубических сантиметров разделить на 1 000 000.
Например, переведём 300 000 000 см3 в кубические метры. Рассуждать в этом случае можно так: «если 1 000 000 см3 это один кубический метр, то сколько раз 300 000 000 см3 будут содержать по 1 000 000 см3»
300 000 000 см3 : 1 000 000 см3 = 300 м3
Пример 2. Выразить 3 м3 в кубических сантиметрах.
Умножим 3 м3 на 1 000 000
3 м3 × 1 000 000 = 3 000 000 см3
Пример 3. Выразить 60 000 000 см3 в кубических метрах.
Узнаем сколько раз 60 000 000 см3 содержит по 1 000 000 см3. Для этого разделим 60 000 000 см3 на 1 000 000 см3
60 000 000 см3 : 1 000 000 см3 = 60 м3
Вместимость бака, банки или канистры измеряют в литрах. Литр это тоже единица измерения объема. Один литр равен одному кубическому дециметру.
1 литр = 1 дм3
Например, если вместимость банки составляет 1 литр, это значит что объём этой банки составляет 1 дм3. При решении некоторых задач может быть полезным умение переводить литры в кубические дециметры и наоборот. Рассмотрим несколько примеров.
Пример 1. Перевести 5 литров в кубические дециметры.
Чтобы перевести 5 литров в кубические дециметры, достаточно умножить 5 на 1
5 л × 1 = 5 дм3
Пример 2. Перевести 6000 литров в кубические метры.
Шесть тысяч литров это шесть тысяч кубических дециметров:
6000 л × 1 = 6000 дм3
Теперь переведём эти 6000 дм3 в кубические метры.
Длина, ширина и высота одного кубического метра равны 10 дм
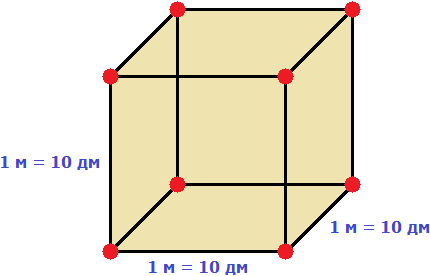
Если вычислить объём этого куба в дециметрах, то получим 1000 дм3
V = 103= 1000 дм3
Получается, что одна тысяча кубических дециметров соответствует одному кубическому метру. А чтобы определить сколько кубических метров соответствуют шести тысячамл кубических дециметров, нужно узнать сколько раз 6 000 дм3 содержит по 1 000 дм3
6 000 дм3 : 1 000 дм3 = 6 м3
Значит, 6000 л = 6 м3.
Таблица квадратов
В жизни часто приходиться находить площади различных квадратов. Для этого каждый раз требуется возводить исходное число во вторую степень.
Квадраты первых 99 натуральных чисел уже вычислены и занесены в специальную таблицу, называемую таблицей квадратов.
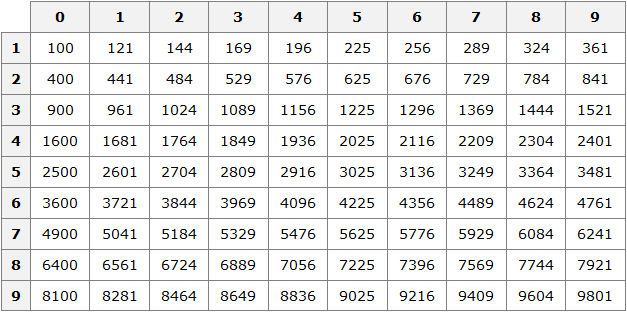
Первая строка данной таблицы (цифры от 0 до 9) это единицы исходного числа, а первый столбец (цифры от 1 до 9) это десятки исходного числа.
Например, найдём квадрат числа 24 по данной таблице. Число 24 состоит из цифр 2 и 4. Точнее, число 24 состоит из двух десятков и четырёх единиц.
Итак, выбираем цифру 2 в первом столбце таблицы (столбце десятков), а цифру 4 выбираем в первой строке (строке единиц). Затем, двигаясь вправо от цифры 2 и вниз от цифры 4, найдём точку пересечения. В результате окажемся на позиции, где располагается число 576. Значит, квадрат числа 24 есть число 576
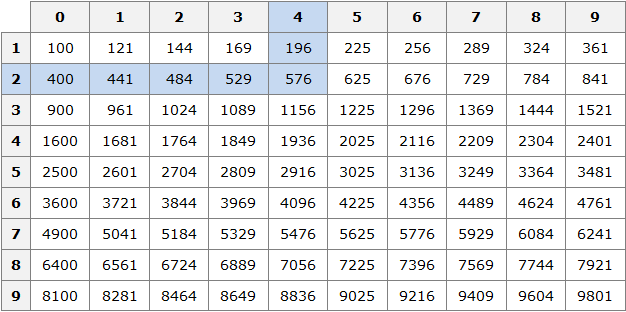
242 = 576
Таблица кубов
Как и в ситуации с квадратами, кубы первых 99 натуральных чисел уже вычислены и занесены в таблицу, называемую таблицей кубов.
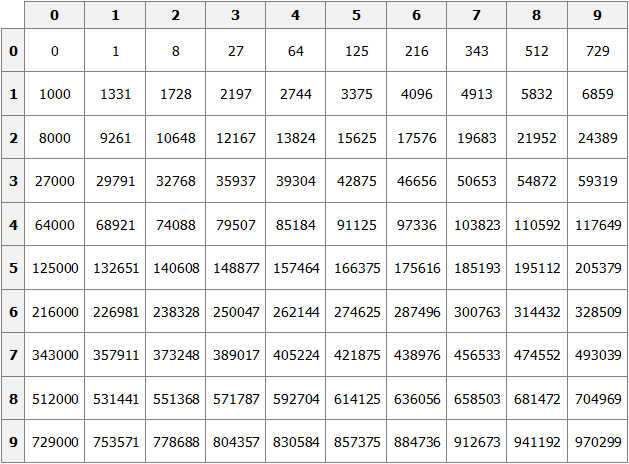
Куб числа по таблице определяется таким же образом, как и квадрат числа. Например, найдём куб числа 35. Это число состоит из цифр 3 и 5. Выбираем цифру 3 в первом столбце таблицы (столбце десятков), а цифру 5 выбираем в первой строке (строке единиц). Двигаясь вправо от цифры 3 и вниз от цифры 5, найдём точку пересечения. В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.
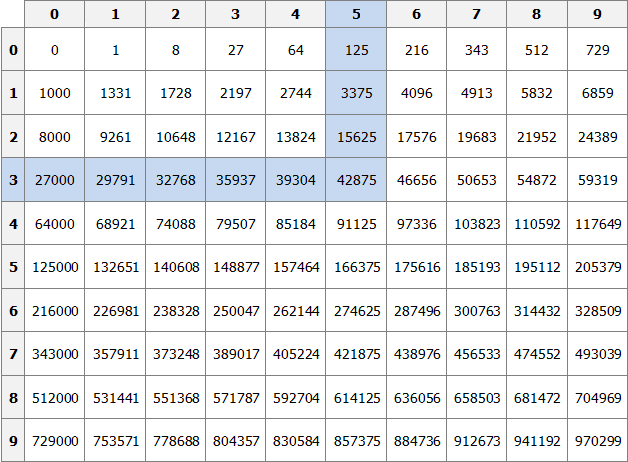
353 = 42875
Задания для самостоятельного решения
Задача 1. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите периметр.
Решение
P = 2(a + b)
a = 6, b = 2
P = 2(6 + 2) = 12 + 4 = 16 см
Ответ: периметр прямоугольника равен 16 см.
Задача 2. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите площадь.
Решение
S = ab
a = 6, b = 2
S = 6 × 2 = 12 см2
Ответ: площадь равна 12 см2.
Задача 3. Площадь прямоугольника составляет 12 см2. Длина составляет 6 см. Найдите ширину прямоугольника.
Решение
S = ab
S = 12, a = 6, b = x
12 = 6 × x
x = 2
Ответ: ширина прямоугольника составляет 2 см.
Задача 4. Вычислите площадь квадрата со стороной 8 см
Решение
S = a2
a = 8
S = 82 = 64 см2
Ответ: площадь квадрата со стороной 8 см равна 64 см2
Задача 5. Вычислите объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см.
Решение
V = abc
a = 6, b = 4, c = 3
V = 6 × 4 × 3 = 72 см3.
Ответ: объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см равен 72 см3
Задача 6. Объем прямоугольного параллелепипеда составляет 200 см3. Найдите высоту параллелепипеда, если его длина равна 10 см, а ширина 5 см
Решение
V = abc
V = 200, a = 10, b = 5, c = x
200 = 10 × 5 × x
200 = 50x
x = 4
Ответ: высота прямоугольного параллелепипеда равна 4 см.
Задача 7. Площади земельного участка, засеянные пшеницей и льном, пропорциональны числам 4 и 5. На какой площади засеяна пшеница, если под льном засеяно 15 га
Решение
Число 4 отражает площадь, засеянную пшеницей. А число 5 отражает площадь, засеянную льном.
Сказано что площади, засеянные пшеницей и льном пропорциональны этим числам.
Проще говоря, во сколько раз изменяются числа 4 или 5, во сколько же раз изменится и площадь, которая засеяна пшеницей или льном. Льном засеяно 15 га. То есть число 5, которое отражает площадь, засеянную льном, изменилось в 3 раза.
Тогда число 4, которое отражает площадь засеянную пшеницей, нужно увеличить в три раза
4 × 3 = 12 га
Ответ: пшеницей засеяно 12 га.
Задача 8. Длина зернохранилища 42 м, ширина составляет  длины, а высота – 0,1 длины. Определите сколько тонн зерна вмещает зернохранилище, если 1 м3 его весит 740 кг.
длины, а высота – 0,1 длины. Определите сколько тонн зерна вмещает зернохранилище, если 1 м3 его весит 740 кг.
Решение
a — длина
b — ширина
c — высота
a = 42 м
b = 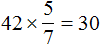 м
м
c = 42 × 0,1 = 4,2 м
Определим объем зернохранилища:
V = abc = 42 × 30 × 4,2 = 5292 м3
Определите сколько тонн зерна вмещает зернохранилище:
5292 × 740 = 3916080 кг
Переведём килограммы в тонны:
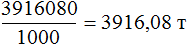
Ответ: зернохранилище вмещает 3916,08 тонн зерна.
Задача 9. 12. Бассейн имеет форму прямоугольного параллелепипеда, длина которого равна 5,8 м, а ширина – 3,5 м. Две трубы наполняют его водой в течение 13 ч 32 мин., причём через одну из них вливается 25 л/мин, а через вторую – 0,75 этого количества. Определите высоту (глубину) бассейна.
Решение
Определим сколько литров в минуту вливается через вторую трубу:
25 л/мин × 0,75 = 18,75 л/мин
Определим сколько литров в минуту вливается в бассейн через обе трубы:
25 л/мин + 18,75 л/мин = 43,75 л/мин
Определим сколько литров воды будет залито в бассейн за 13 ч 32 мин
43,75 × 13 ч 32 мин = 43,75 × 812 мин = 35 525 л
1 л = 1 дм3
35 525 л = 35 525 дм3
Переведём кубические дециметры в кубические метры. Это позволит вычислит объем бассейна:
35 525 дм3 : 1000 дм3 = 35,525 м3
Зная объём бассейна можно вычислить высоту бассейна. Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:
V = 35,525
a = 5.8
b = 3.5
c = x
35,525 = 5,8 × 3,5 × x
35,525 = 20,3 × x
x = 1,75 м
с = 1,75
Ответ: высота (глубина) бассейна составляет 1,75 м.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже


Загрузить PDF
Загрузить PDF
Площадь поверхности – это суммарная площадь всех поверхностей, которые составляют объемную фигуру. Площадь поверхности является числовой характеристикой поверхности.[1]
Вычислить площадь поверхности объемной (трехмерной) фигуры довольно просто, если знать соответствующую формулу. Существует определенная формула для каждой фигуры, поэтому сначала нужно определить, какая фигура дана. Чтобы быстро вычислять площадь поверхности, запомните соответствующие формулы для разных фигур. В данной статье рассматриваются наиболее распространенные фигуры.
-

1
Запишите формулу для вычисления площади поверхности куба. У куба шесть равных квадратных граней. Так как стороны квадрата равны, площадь квадрата равна a2, где а – сторона. Так как у куба шесть равных квадратных граней, чтобы найти площадь поверхности, умножьте площадь одной грани (квадрата) на 6. Формула для вычисления площади поверхности (SA) куба: SA = 6а2, где а – ребро куба (сторона квадрата).[2]
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-

2
Измерьте ребро куба. Ребра куба равны, поэтому можно измерить только одно (любое) ребро. Ребро измерьте с помощью линейки (или рулетки). Обратите внимание на используемые единицы измерения.
- Запишите значение, обозначив его через а.
- Например: а = 2 см
-

3
Значение а возведите в квадрат. То есть возведите в квадрат длину ребра куба. Для этого умножьте значение на себя. Если вы только приступили к изучению формул с квадратами, запишите формулу так: SA = 6*а*а.
- Сейчас вы вычислили значение площади одной из граней куба.
- Например: а = 2 см
- a2 = 2 х 2 = 4 см2
-

4
Вычисленное значение умножьте на шесть. Помните, что у куба шесть равных граней. Вычислив площадь одной из граней, умножьте полученное значение на 6, чтобы включить все грани куба.
- Это последний шаг в процессе вычисления площади поверхности куба.
- Например: а 2 = 4 см2
- SA = 6 х а2 = 6 х 4 = 24 см2
Реклама
-

1
Запишите формулу для вычисления площади поверхности прямоугольной призмы. У прямоугольной призмы шесть граней, причем равными являются только противоположные грани.[3]
Поэтому формула для вычисления площади поверхности прямоугольной призмы включает значения трех разных ребер: SA = 2ab + 2bc + 2ac.- Здесь а – ширина, b – высота, с – длина призмы.
- Если проанализировать формулу, можно понять, что она суммирует площади всех граней.
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-

2
Найдите значения высоты, ширины и длины призмы. Три ребра не являются равными, поэтому нужно выполнить три измерения. Измерьте соответствующие ребра с помощью линейки (или рулетки). Ребра измеряйте в одной единице измерения.
- Измерьте длину грани, которая лежит в основании призмы; длину обозначьте через с.
- Например: с = 5 см
- Измерьте ширину грани, которая лежит в основании призмы; ширину обозначьте через а.
- Например: а = 2 см
- Измерьте высоту призмы; высоту обозначьте через b.
- Например: b = 3 см
-

3
Вычислите площадь одной грани призмы, а затем полученное значение умножьте на два. Помните, что у прямоугольной призмы шесть граней, причем равными являются только противоположные грани. Умножьте длину на высоту (с на а), чтобы найти площадь одной грани. Затем полученное значение умножьте на 2, чтобы включить вторую (противоположную и равную) грань.[4]
- Например: 2 x (a x c) = 2 x (2 x 5) = 2 x 10 = 20 см2
-

4
Вычислите площадь другой грани призмы, а затем полученное значение умножьте на два. Умножьте ширину на высоту (а на b), чтобы найти площадь другой грани. Затем полученное значение умножьте на 2, чтобы включить вторую (противоположную и равную) грань.[5]
- Например: 2 x (a x b) = 2 x (2 x 3) = 2 x 6 = 12 см2
-

5
Вычислите площадь фронтальной грани, а затем полученное значение умножьте на два. Умножьте длину на ширину (с на b), чтобы найти площадь фронтальной грани. Затем полученное значение умножьте на 2, чтобы включить вторую (противоположную и равную) грань.[6]
- Например: 2 x (b x c) = 2 x (3 x 5) = 2 x 15 = 30 см2
-

6
Сложите три значения. Так как площадь поверхности – это суммарная площадь всех граней фигуры, сложите найденные значения площадей отдельных граней. Вы получите площадь поверхности прямоугольной призмы.[7]
- Например: SA = 2ab + 2bc + 2ac = 12 + 30 + 20 = 62 см2
Реклама
-

1
Запишите формулу для вычисления площади поверхности треугольной призмы. Треугольная призма имеет две равные треугольные грани и три прямоугольные грани. Чтобы вычислить площадь поверхности треугольной призмы, нужно найти площади всех граней и сложить их. Формула для вычисления площади поверхности треугольной призмы: SA = 2S + РH, где S – площадь треугольной грани, Р – периметр треугольной грани, H – высота призмы.[8]
- Здесь S – это площадь треугольника (треугольной грани), которая вычисляется по формуле S = 1/2bh, где b – основание треугольника, h – высота треугольника (которая опущена на основание).
- Р – периметр треугольника (треугольной грани), который равен сумме всех сторон треугольника.
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-

2
Вычислите площадь треугольной грани и умножьте ее на два. Площадь треугольника вычисляется по формуле S = 1/2bh, где b – основание треугольника, h – высота треугольника (которая опущена на основание). Так как треугольная призма имеет две равные треугольные грани, эту формулу можно умножить на два. Поэтому, чтобы вычислить площади двух треугольных граней, просто перемножьте основание и высоту треугольника (b*h).[9]
- Основание треугольника b – это его нижняя сторона.
- Например: b = 4 см
- Высота треугольника h – это перпендикуляр, опущенный на основание из противоположной вершины.
- Например: h = 3 см
- Площадь двух треугольных граней равна: 2(1/2)b*h = b*h = 4*3 =12 см.
-

3
Измерьте каждую сторону треугольника и высоту призмы. Чтобы вычислить площадь поверхности треугольной призмы, нужно найти значение каждой стороны треугольника и высоты призмы. Высота призмы – это расстояние между треугольными гранями.
- Например: Н = 5 см
- Стороны треугольника – это три ребра одной (любой) из треугольных граней.
- Например: а = 2 см, b = 4 см, с = 6 см
-

4
Вычислите периметр треугольника. Для этого сложите все стороны треугольника: Р = а + b + с.
- Например: P = а + b + с = 2 + 4 + 6 = 12 см
-

5
Перемножьте периметр треугольной грани и высоту призмы. Помните, что высота призмы – это расстояние между треугольными гранями. Таким образом, Р умножьте на Н.
- Например: Р х Н = 12 х 5 = 60 см2
-

6
Сложите полученные значения. Чтобы найти площадь поверхности треугольной призмы, сложите два значения, вычисленные ранее.[10]
- Например: 2S + PH = 12 + 60 = 72 см2
Реклама
-

1
Запишите формулу для вычисления площади поверхности шара. Шар имеет изогнутую поверхность, поэтому формула включает математическую константу π (число Пи). Чтобы вычислить площадь поверхности шара, воспользуйтесь формулой SA = 4π*r2.[11]
- Здесь r – радиус шара, π ≈ 3,14.
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-

2
Измерьте радиус шара. Радиус шара равен половине его диаметра, то есть половине отрезка, который проходит через центр шара и соединяет две точки, лежащие на его поверхности.[12]
- Например: r = 3 см
-

3
Радиус шара возведите в квадрат. Для этого умножьте значение радиуса (r) на себя. Помните, что формулу можно записать так: SA = 4π*r*r.[13]
- Например: r2 = r x r = 3 x 3 = 9 см2
-

4
Перемножьте квадрат радиуса и приблизительное значение числа Пи. Число Пи является математической константой, которая равна отношению длины окружности к ее диаметру.[14]
Это иррациональное число со множеством цифр после десятичной запятой. Зачастую число Пи округляется до 3,14. Квадрат радиуса умножьте на π (на 3,14), чтобы вычислить площадь круглого сечения шара. [15]
- Например: π*r2 = 3,14 x 9 = 28,26 см2
-

5
Полученное значение умножьте на четыре. Чтобы найти значение площади поверхности сферы, площадь круглого сечения умножьте на 4.[16]
- Например: 4π*r2 = 4 x 28,26 = 113,04 см2
Реклама
-

1
Запишите формулу для вычисления площади поверхности цилиндра. Цилиндрическая поверхность этой фигуры ограничена двумя круглыми параллельными плоскостями, которые называются основаниями. Формула для вычисления площади поверхности цилиндра: SA = 2π*r2 + 2π*rh, где r – радиус основания, h – высота цилиндра, π ≈ 3,14.[17]
- 2π*г2 – это площадь двух оснований, а 2πrh – это площадь цилиндрической поверхности.
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-

2
Измерьте радиус основания и высоту цилиндра. Радиус окружности равен половине ее диаметра, то есть половине отрезка, который проходит через центр окружности и соединяет две точки, лежащие на ней.[18]
Высота цилиндра – это расстояние между его основаниями. Измерьте и запишите радиус основания и высоту цилиндра.- Например: r = 3 см
- Например: h = 5 см
-

3
Вычислите площадь основания и умножьте ее на два. Чтобы найти площадь основания, воспользуйтесь формулой для вычисления площади круга: S = π*г2. Сначала радиус возведите в квадрат, а затем полученное значение умножьте на число Пи. Результат умножьте на два, чтобы учесть второе равное основание.[19]
- Например: площадь основания = π*r2 = 3,14 х 3 х 3 = 28,26 см2
- Например: 2π*r2 = 2 x 28,26 = 56,52 см2
-

4
Вычислите площадь цилиндрической поверхности. Для этого воспользуйтесь формулой S = 2π*rh, по которой можно найти площадь поверхности трубы. Здесь труба – это поверхность между двумя основаниями цилиндра. Перемножьте двойку, число Пи, радиус и высоту.[20]
- Например: 2π*rh = 2 x 3,14 x 3 x 5 = 94,2 см2
-

5
Сложите полученные значения. Сложите площади двух оснований и площадь цилиндрической поверхности (между двумя основаниями), чтобы вычислить общую площадь поверхности цилиндра. Обратите внимание, что при сложении этих величин получится исходная формула: SA = 2π*r2 + 2π*rh.[21]
- Например: 2π*r2 + 2π*rh = 56,52 + 94,2 = 150,72 см2
Реклама
-

1
Запишите формулу для вычисления площади поверхности квадратной пирамиды. Квадратная пирамида имеет одно квадратное основание и четыре треугольные грани. Помните, что площадь квадрата равна квадрату его стороны. Площадь треугольника равна 1/2sl (половина основания треугольника, умноженная на его высоту). Так как пирамида имеет четыре треугольные грани, нужно площадь треугольника умножить на 4. Таким образом, площадь поверхности квадратной пирамиды вычисляется по формуле: SA = s2 + 2sl.[22]
- В этой формуле s – ребро квадратной грани (сторона квадрата), l – апофема пирамиды.
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-

2
Найдите значения апофемы и ребра квадратной грани. Апофема (l) – это высота треугольной грани, то есть расстояние между основанием треугольника и его вершиной. Ребро квадратной грани (s) – это сторона квадрата. Помните, что у квадрата все стороны равны, поэтому измерьте любое ребро квадратной грани, а также измерьте апофему пирамиды.[23]
- Например: l = 3 см
- Например: s = 1 см
-

3
Найдите площадь квадратной грани. Для этого возведите в квадрат ребро этой грани (сторону квадрата), то есть умножьте значение s на себя.[24]
- Например: s2 = s х s = 1 х 1 = 1 см2
-

4
Вычислите общую площадь четырех треугольных граней. Вторая часть формулы включает суммарную площадь четырех треугольных граней. Согласно формуле 2ls, перемножьте 2, s и l. Так вы найдете суммарную площадь 4-х треугольных граней.[25]
- Например: 2 х s х l = 2 х 1 х 3 = 6 см2
-

5
Сложите полученные значения. Сложите площадь квадратной грани и общую площадь четырех треугольных граней, чтобы вычислить площадь поверхности пирамиды.[26]
- Например: s2 + 2sl = 1 + 6 = 7 см2
Реклама
-

1
Запишите формулу для вычисления площади поверхности конуса. Конус имеет круглое основание и закругленную боковую поверхность, которая сужается в вершине этой фигуры. Чтобы найти площадь поверхности конуса, нужно вычислить значения площади круглого основания и площади боковой поверхности, а затем сложить эти значения. Формула для вычисления площади поверхности конуса: SA = π*r2 + π*rl, где r – радиус круглого основания, l – образующая (расстояние между вершиной конуса и точкой, которая лежит на окружности круга), π ≈ 3,14.[27]
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-

2
Измерьте радиус основания и высоту конуса. Радиус – это отрезок, соединяющий центр круга и точку, которая лежит на его окружности. Высота – это расстояние между центром круга и высотой конуса.[28]
- Например: r = 2 см
- Например: h = 4 см
-

3
Найдите значение образующей конуса (l). Образующая конуса является гипотенузой треугольника, поэтому воспользуйтесь теоремой Пифагора, чтобы вычислить образующую: l = √(r2 + h2), где r – радиус круглого основания, h – высота конуса.[29]
- Например: l = √(r2 + h2) = √(2 х 2 + 4 х 4) = √(4 + 16) = √(20) = 4,47 см
-

4
Вычислите площадь круглого основания. Площадь круга вычисляется по формуле S = π*r2. Измерив радиус, возведите его в квадрат (умножьте r на себя), а затем квадрат радиуса умножьте на число Пи.[30]
- Например: π*r2 = 3,14 x 2 x 2 = 12,56 см2
-

5
Вычислите площадь боковой поверхности конуса. Сделайте это по формуле S = π*rl, где r – радиус круга, l – образующая, которая найдена ранее.[31]
- Например: π*rl = 3,14 x 2 x 4,47 = 28,07 см
-

6
Сложите полученные значения, чтобы найти площадь поверхности конуса. Площадь поверхности конуса равна сумме площади круглого основания и площади боковой поверхности конуса.[32]
- Например: π*r2 + π*rl = 12,56 + 28,07 = 40,63 см2
Реклама
Что вам понадобится
- Линейка
- Ручка или карандаш
- Бумага
Об этой статье
Эту страницу просматривали 69 612 раз.
Была ли эта статья полезной?
Площадь фигуры является суммарной числовой характеристикой всех единичных квадратных элементов плоскости. В зависимости от размера фигур стороны квадрата единичного элемента могут быть равны 1 мм, см, м, дюйму, км и пр. S фигур могут измеряться в следующих единицах измерения: мм2, см2, м2, гектарах, квадратных километрах и пр.
Площадь фигуры сложной формы может составляться из различных элементарных фигур: треугольников, квадратов, прямоугольников и пр. Общая площадь будет высчитываться путем суммирования площадей составляющих компонент.
Набор онлайн-калькуляторов страницы дает возможность оперативного вычисления не только S плоских фигур (квадрата, прямоугольника, круга, ромба, эллипса), но и площадей объемных фигур (куба, призмы, конуса, цилиндра, сферы, тетраэдра и пр.), являющихся совокупностью нескольких плоскостей.
Вычисление площадей фигур востребовано для решения различных задач:
– строительных;
– кадастровых;
– инженерных и пр.
Государство осуществляет кадастровый учет земельных участков, основным учитываемым параметром которых является площадь. Специалистами БТИ фиксируется общая и полезная жилая площадь квартир. В быту иногда нужно вычислять площадь ковра, натяжного потолка, площадь дачного участка и пр.
Форма объекта и его линейные размеры определяют один из важных с геометрической точки зрения параметров — объём. Формула для прямоугольника, позволяющая его вычислить, довольно проста и основана на знании стороны и высоты. Но при решении не всегда известны значения рёбер фигуры, поэтому приходится использовать свойства параллелограмма, а именно — способы нахождения площади.
Общие сведения
По своей сути объём является количественной характеристикой пространства, которое занимает тело или вещество. Простыми словами, этот параметр показывает вместимость. В качестве единицы измерения, согласно СИ, принят кубический метр. За обозначение же объёма взята латинская буква V.
У тел, имеющих простую форму, характеристики находятся путём перемножения площади на высоту. Например, для куба он равен a3, прямоугольной призмы — h * b * a, пирамиды — (S * b * h) / 3. В эллипсоидных фигурах при расчётах используется радиус. Так, для конуса объём равен (p * R2 * h) / 3, сферы — (4 * p * R3) / 3, тора — 2 * p2 * R1 * R22.
Объём плоских фигур, таких как треугольник, круг, квадрат, прямоугольник, равен нулю. Но если их стороны или окружности имеют связанные с ними попарно параллельные линии, то они уже являются объёмными фигурами. Например, прямоугольник в пространстве называют параллелепипедом. Таким образом, чтобы найти объём прямоугольника, необходимо, чтобы он представлял собой прямоугольный параллелепипед, иначе действие будет бессмысленным.
Определить объём — значит, знать две основные величины фигуры:

- площадь — двумерная характеристика, определяющая размер фигуры,
- высоту — это длина перпендикуляра, опущенного из вершины на основание в трёхмерном пространстве.
Так как площадь измеряется в метрах квадратных, а высота просто в метрах, то перемножение площади и высоты как раз и даст единицу измерения объёма — метр кубический.
Решение задач
На самом деле вычисление объёма не только выполняют на уроках математики. Это знание востребовано в довольно многих специальностях и науках. Например, при строительстве, в архитектуре, инженерии, физике, химии. Поэтому знание нахождения параметра может пригодиться не только в школе. Теорию обязательно необходимо закреплять на практике. Вот некоторые задачи, которые помогут усвоить рассматриваемый материал:
- Пусть есть параллелепипед с прямыми сторонами. Его рёбра у основания равняются 19 и 20 сантиметрам. Размер же боковой грани составляет 10 сантиметров. Вычислить объём фигуры. Эта задача на одну формулу, все данные для подстановки в неё известны. Так, V = a * b * c = 19 * 20 * 10 = 3 800 см3 = 0,0038 м³.
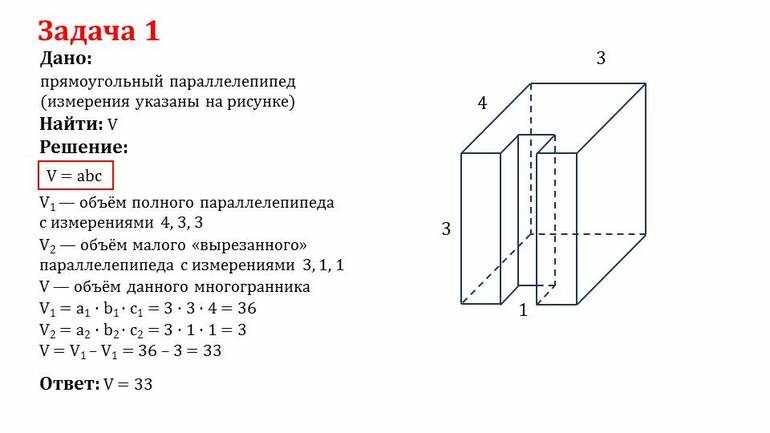
- Пусть имеется параллелепипед с основанием 1 см на 1,2 см и высотой 0,8 см. Из него был удалено другое прямоугольное тело с размерами 0,3 x 0,55 x 0,5. Найти объём получившейся фигуры. Так как искомый параметр новой фигуры равен разнице изначального и удалённого объёмов, то зная формулу найти ответ не составит труда: V = 0,8 * 1 * 1,2 — 0,3 * 0,5 * 0,55 = 0,877 см3.
- Дан прямоугольный параллелепипед с вершинами ABCD и A1B1C1D1. Сравнить объём образованного в середине пирамиды AA1BD тела со значением фигуры. Для удобства решения стороны AB, AD, AA соответственно можно обозначить как x, y, z. Тогда объём прямоугольного тела будет равен Vп = Sп * AA1 = x * y * z. Если начертить условие на рисунке, то можно отметить, что площадь пирамиды вполовину меньше площади основания прямоугольника. То есть, Sabd = 0,5 * Sabd. Тогда V = Sabd * AA1 / 3 = x * y * z / 3 * 2 = x * y* z / 6. Значит, объём вписанной пирамиды меньше в шесть раз чем у фигуры.
- В гальванической ванне помещается три тысячи литров раствора. Высота наполнения ёмкости при этом достигает 75 сантиметров. В ванную поместили заготовку, после чего уровень поднялся на два сантиметра. Найти объём заготовки в метрах кубических. Итак, в одном кубическом метре содержится тысяча литров. Поэтому изначально в ёмкости было 3 м³ раствора. Значит, изначально в ванне раствор занимал: 3 = S * 75. Отсюда s = 3/75 = 1/25 см2. Объём детали составляет: V = S * 2 = (1/25) * 2 = 2 / 25 = 0,08 м³.
Использование калькулятора
Конечно же, на обычном калькуляторе объём прямоугольника не подсчитаешь. Разве что известны три его грани и формула нахождения параметра. Тогда нужно будет просто перемножить три числа. В других же случаях, когда нужно решить сложную задачу, связанную с громоздкими вычислениями, можно использовать математические сайты, имеющие название онлайн-калькуляторы.
Это интернет-сервисы, предлагающие своим пользователям бесплатно воспользоваться услугами по вычислению объёма геометрических фигур и выполнить другие математические операции. Для того чтобы воспользоваться сайтами-решателями, нужно иметь любой гаджет с возможностью подключения его к интернету и установленным на него веб-обозревателем.
После загрузки онлайн-калькулятора все действия пользователя сводятся к заполнению специальной формы в которую вносится условие задания. Конечно же, такое решение не может называться самостоятельным, но для проверки полученного результата или выявления ошибок в расчёте подходит идеально. Кроме, непосредственно автоматического вычисления объёма большинство сайтов содержат на своих страницах теоретический материал, а также примеры решений типовых заданий. Так что при обучении учащихся их использование на первых порах вполне оправданно.
