Загрузить PDF
Загрузить PDF
Определить площадь плоских фигур в квадратных сантиметрах (также обозначаемых как см2) достаточно просто. В самом легком случае, когда требуется рассчитать площадь квадрата или прямоугольника, она вычисляется произведением длины и ширины. Площадь других фигур (кругов, треугольников и так далее) можно определить с помощью целого ряда специальных математических формул. Также, если потребуется, можно без труда перевести площадь в квадратные сантиметры из других единиц измерения.
-

1
Определите длину измеряемой площади. У квадратов и прямоугольников по четыре стороны, расположенных под прямыми углами относительно друг друга. В случае с прямоугольниками, их противоположные стороны равны между собой, тогда как у квадратов равны все стороны. Измерьте одну из сторон квадрата или большую из сторон прямоугольника, чтобы определить ее длину в сантиметрах.[1]
-

2
Определите ширину измеряемой площади. Далее измерьте в сантиметрах любую из сторон, смежных с той, которую вы измерили в первую очередь. Эта сторона будет находиться под углом в 90 градусов к первой. Вторая мерка будет обозначать ширину квадрата или прямоугольника.[2]
- Так как у квадрата все стороны одинаковы, его длина будет равна ширине. Поэтому у квадрата можно изначально измерить только одну сторону.
-

3
Умножьте длину на ширину. Просто перемножьте длину и ширину фигуры, чтобы определить площадь квадрата или прямоугольника в квадратных сантиматрах.[3]
- Например, допустим, что длина прямоугольника составляет 4 см, а ширина – 3 см. В таком случае площадь фигуры рассчитывается следующим образом: 4 × 3 = 12 квадратных сантиметров.
- В случае с квадратом (по причине равных сторон) можно просто умножить саму на себя длину одной из его сторон (другими словами, возвести ее “в квадрат” или “во вторую степень”), чтобы определить площадь фигуры в квадратных сантиметрах.
Реклама
-

1
Найдите площадь круга по формуле: S = π × r2. Чтобы найти площадь круга в квадратных сантиметрах, необходимо знать расстояние в сантиметрах от центра круга до линии его окружности. Это расстояние называется радиусом окружности. Как только радиус будет известен, обозначьте его буквой r из вышеупомянутой формулы. Умножьте значение радиуса само на себя и на число π (3,1415926…), чтобы узнать площадь круга в квадратных сантиметрах.[4]
- Например, площадь круга с радиусом 4 см составит 50,27 квадратных сантиметра в результате перемножения 3,14 и 16.
-

2
Вычислите площадь треугольника по формуле: S = 1/2 b × h. Площадь треугольника в квадратных сантиметрах вычисляется умножением половины длины его основания b (в сантиметрах) на его высоту h (в сантиметрах). Основанием треугольника выбирается одна из его сторон, тогда как высота треугольника – это перпендикуляр, опущенный к основанию треугольника из противоположной к нему вершины. Площадь треугольника можно вычислить через длину основания и высоту по любой из сторон треугольника и противоположной к ней вершине.[5]
- Например, если длина основания треугольника составляет 4 см, а высота, проведенная к основанию – 3 см, площадь составит: 2 x 3 = 6 квадратных сантиметра.
-

3
Найдите площадь параллелограмма по формуле: S = b × h. Параллелограммы подобны прямоугольникам за одним исключением – их углы не обязательно равны 90 градусам. Соответственно, расчет площади параллелограмма производится аналогичным для прямоугольника способом: длина стороны основания в сантиметрах умножается на высоту параллелограмма в сантиметрах. За основание берут любую из сторон, а высота определяется длиной перпендикуляра к ней из противоположного тупого угла фигуры.[6]
- Например, если длина основания параллелограмма составляет 5 см, а его высота – 4 см, его площадь составит: 5 x 4 = 20 квадратных сантиметров.
-

4
Вычислите площадь трапеции по формуле: S = 1/2 × h × (B+b). Трапеция – это четырехугольник две стороны которого параллельны между собой, а остальные две – нет. Чтобы определить площадь трапеции в квадратных сантиметрах, необходимо знать три мерки (в сантиметрах): длину более длинной параллельной стороны B, длину более короткой параллельной стороны b и высоту трапеции h (определяемую как кратчайшее расстояние между ее параллельными сторонами по перпендикулярному к ним отрезку). Сложите между собой длины двух параллельных сторон, поделите сумму пополам и умножьте на высоту, чтобы получить площадь трапеции в квадратных сантиметрах.[7]
- Например, если более длинная из параллельных сторон трапеции равна 6 см, более короткая – 4 см, а высота – 5 см, площадь фигуры составит: ½ x (6+4) х 5 = 25 квадратных сантиметров.
-

5
Найдите площадь правильного шестиугольника: S = ½ × P × a. Приведенная формула верна только для правильного шестиугольника с шестью равными сторонами и шестью одинаковыми углами. Буквой P обозначается периметр фигуры (или произведение длины одной стороны на шесть, что справедливо для правильного шестиугольника). Буквой a обозначается длина апофемы – расстояние от центра шестиугольника до середины одной из его сторон (точки, расположенной посередине между двумя соседними вершинами фигуры). Перемножьте периметр и апофему в сантиметрах и поделите результат на два, чтобы найти площадь правильного шестиугольника.[8]
- Например, если у правильного шестиугольника шесть равных сторон по 4 см (то есть его периметр P = 6 x 4 = 24 см), а длина апофемы равна 3,5 см, то его площадь составит: ½ x 24 x 3,5 = 42 квадратных сантиметра.
-

6
Вычислите площадь правильного восьмиугольника по формуле: S = 2a² × (1 + √2). Для расчета площади правильного восьмиугольника (с восемью равными сторонами и восемью одинаковыми углами) нужно знать только длину одной из сторон фигуры в сантиметрах (обозначенной в формуле буквой “a”). Подставьте соответствующее значение в формулу и вычислите результат.[9]
- Например, если длина стороны правильного восьмиугольника равна 4 см, то площадь этой фигуры составляет: 2 х 16 x (1 + 1,4) = 32 x 2,4 = 76,8 квадратных сантиметров.
Реклама
-

1
Переведите все мерки в сантиметры, прежде чем производить расчет площади. Чтобы сразу рассчитать площадь в квадратных сантиметрах, необходимо подставлять все параметры в формулу расчета площади также в сантиметрах (это касается, длины, высоты, апофемы и так далее). Поэтому, если ваши исходные данные выражены в других единицах измерения (например, в метрах), сначала их следует перевести в сантиметры. Ниже приведены соотношения наиболее популярных единиц измерения.
- 1 метр = 100 сантиметров
- 1 сантиметр = 10 миллиметров
- 1 дюйм = 2,54 сантиметра
- 1 фут = 30,48 сантиметра
- 1 сантиметр = 0,3937 дюйма
-

2
Чтобы перевести площадь из квадратных метров в квадратные сантиметры, ее следует умножить на 10000 (то есть площадь одного квадратного метра в сантиметрах), или на произведение 100 см на 100 см. Если вы знаете площадь фигуры в квадратных метрах, ее можно перевести в квадратные сантиметры умножением на 10000.[10]
- Например, 0,5 квадратного метра = 0,5 x 10000 = 5000 квадратных сантиметров.
-

3
Чтобы перевести в квадратные сантиметры площадь, выраженную в квадратных дюймах, умножьте ее на 6,4516. Как уже упоминалось, 1 дюйм равен 2,54 сантиметра, тогда как квадратный дюйм составляет 6,4516 квадратных сантиметров (или 2,54 x 2,54). Таким образом, если вам необходимо конвертировать в квадратные сантиметры площадь, равную 10 квадратным дюймам, следует умножить 10 на 6,4516, и у вас получится 64,5 квадратных сантиметров.[11]
- Также следует упомянуть, что в одном гектаре содержится 10000 квадратных метров, тогда как каждый квадратный метр равен 10000 квадратных сантиметров. Поэтому, чтобы выразить один гектар в сантиметрах, следует умножить 10000 на 10000 и получится 100 миллионов квадратных сантиметров.
Реклама
Об этой статье
Эту страницу просматривали 153 792 раза.
Была ли эта статья полезной?
Рассмотрим фигуру ниже:
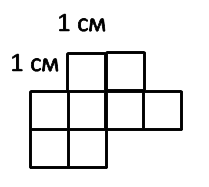
Вся фигура состоит из 8 квадратов со стороной 1 см каждый.
Площадь одного такого квадрата называют квадратным сантиметром и записывают:
1 см2.
Площадь всей фигуры 8 см2.
Запомните!
![]()
Площадь измеряется только в квадратных единицах длины. Всегда проверяйте свои ответы.
В математике для нахождения площади геометрических фигур используют специальные формулы,
в которых площадь обозначается заглавной латинской буквой «S».
Напоминаем, что площадь квадрата можно найти, умножив длину его стороны на саму себя.
Единицей площади служит площадь единичного квадрата. Например, если длина стороны квадрата,
равна 1 м, то его площадь равна 1
квадратному метру (1 м2); если длина
его стороны равна 1 см, то его площадь
равна 1 квадратному сантиметру
(1 см2).
Для нахождения площади какой-либо фигуры её сравнивают с единичным квадратом.
Как перевести квадратные единицы
Рассмотрим квадрат со стороной 1 см.
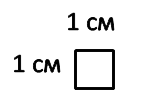
Его площадь равна:
S = 1 см · 1 см = 1см2
Рассмотрим квадрат со стороной 1 м.
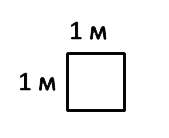
Его площадь равна:
S = 1 м · 1 м = 1 м2
Известно, что: 1 м = 100 см
1 м2 = 1 м · 1 м = 100 см · 100 см = 10 000 см2
Увеличим сторону квадрата равную 1 м в
10 раз. Получим квадрат со
стороной 10 м.
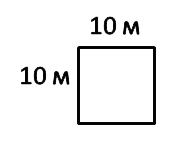
Площадь такого квадрата называют ар или сотка.
S = 10 м · 10 м = 100 м2
В одном аре — сто квадратных метров.
Слово «сотка» часто используют в дачном хозяйстве, хотя это тоже самое, что и «ар».
1 ар (сотка) = 100 м2
Чтобы выразить ар в cм2, вспомним, что 1 м2 = 10 000 см2.
Значит: 1 ар (сотка) = 100 м2 = 100 · 10 000 см2 = 1 000 000 см2
Увеличим сторону квадрата равную 10 м в 10 раз.
Получим квадрат со
стороной 100 м.
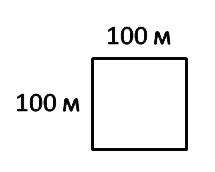
Площадь такого квадрата называют гектар. Сокращенно «га». Но при произношении вслух наименование
проговаривается полностью.
Выразим гектар в квадратных метрах.
1 га = 100 м · 100 м = 10 000 м2
Теперь определим, сколько в одном гектаре аров.
1 ар = 100 м2
Значит: 10 000 м2 : 100 м2 = 100 (ар)
1 га = 100 ар
Для измерения больших площадей, например, территорий государств, материков используют квадратный километр.
То есть квадрат со стороной 1 км и
площадью 1 км2.
1 км = 1000 м
1 км2 = 1 км · 1 км = 1 000 м · 1 000 м = 1 000 000 м2
Для простоты расчётов предлагаем вам в помощь таблицу переводов квадратных единиц.
Таблица переводов квадратных единиц
Данная таблица поможет перевести гектары в кв. метры, гектары в ары и наоборот.
| га | ар | м2 | cм2 | |
|---|---|---|---|---|
| 1 км2 | 100 га | 10 000 ар | 1 000 000 м2 | 1 000 000 000 cм2 |
| 1 га | 1 га | 100 ар | 10 000 м2 | 100 000 000 cм2 |
| 1 ар | 0,01 га | 1 ар | 100 м2 | 1 000 000cм2 |
| 1 м2 | 0,000 1 га | 0,01 ар | 1 м2 | 10 000 cм2 |
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
12 сентября 2018 в 20:57
Дмитрий Мозговой

Профиль
Благодарили: 0
Сообщений: 1

Дмитрий Мозговой
Профиль
Благодарили: 0
Сообщений: 1
Внутри большего квадрата расположен меньший квадрат площади 73. Известно, что длины отрезков, на которые сторона большего квадрата делится вершинами меньшего квадрата, — натуральные числа. Чему равна площадь большего квадрата?
0
Спасибо
Ответить
14 октября 2018 в 20:45
Ответ для Дмитрий Мозговой
Дарья Тихая

Профиль
Благодарили: 0
Сообщений: 1

Дарья Тихая
Профиль
Благодарили: 0
Сообщений: 1
146
0
Спасибо
Ответить
21 октября 2018 в 15:44
Ответ для Дмитрий Мозговой
Владимир Шварцман

Профиль
Благодарили: 0
Сообщений: 1

Владимир Шварцман
Профиль
Благодарили: 0
Сообщений: 1
Пусть отрезки большего квадрата a и в. Тогда а2 + в2 =73 Сумма двух чисел нечётна если одно чёт., а второе нечёт. Это 1,9,25,49 и 4, 16,36.64 Легко видеть, что это числа 9 и 64.Т.е. а=3 и в=8 Пл. большого квадрата=112 =121
0
Спасибо
Ответить
12 ноября 2018 в 3:31
Ответ для Дмитрий Мозговой
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Неверно.
0
Спасибо
Ответить
22 июня 2016 в 20:17
Клара Чукаева

Профиль
Благодарили: 0
Сообщений: 1

Клара Чукаева
Профиль
Благодарили: 0
Сообщений: 1
д вечер. у меня вопрос: как найти площадь таблички размером 50 см на 75 см? если перемножить, как нам предлагает школьная программа, то получается 3750 см2, разве это возможно? я ошибаюсь? напишите формулу для расчета пожалуйста?
0
Спасибо
Ответить
24 июня 2016 в 12:18
Ответ для Клара Чукаева
Павел Асафов

Профиль
Благодарили: 0
Сообщений: 2

Павел Асафов
Профиль
Благодарили: 0
Сообщений: 2
Здравствуйте! Все верно.
Формула площади прямоугольника S=a · b
(a)50 · (b)75=3750 см2
Может вы спутали с периметром? Периметр будет равен 250 см
a ·2+b · 2
0
Спасибо
Ответить
16 января 2016 в 18:29
Надюша Бисерова

Профиль
Благодарили: 0
Сообщений: 1

Надюша Бисерова
Профиль
Благодарили: 0
Сообщений: 1
ширина прамоугольника 23 см. на сколько увеличиться площадь прамоугольника, если его длину увеличить на 3 см?
подскажите решение пожалуйста
0
Спасибо
Ответить
21 января 2016 в 16:17
Ответ для Надюша Бисерова
Сергей Фадеев

Профиль
Благодарили: 0
Сообщений: 6

Сергей Фадеев
Профиль
Благодарили: 0
Сообщений: 6
на 3 см квадратных
если я не ошибаюсь взависимости от длины
0
Спасибо
Ответить
24 января 2016 в 13:50
Ответ для Надюша Бисерова
Инна Шабрашина

Профиль
Благодарили: 0
Сообщений: 5

Инна Шабрашина
Профиль
Благодарили: 0
Сообщений: 5
увеличится на 69
0
Спасибо
Ответить
12 октября 2015 в 17:22
Мося Мося

Профиль
Благодарили: 0
Сообщений: 1

Мося Мося
Профиль
Благодарили: 0
Сообщений: 1
найди площадь квадрата периметр которого 280см
0
Спасибо
Ответить
1 июля 2016 в 14:20
Ответ для Мося Мося
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Для нахождения площади квадрата в данном случае нам понадобятся две формулу, а именно:
1) Формула периметра квадрата P=4a. Подробно про периметр читаем здесь http://math-prosto.ru/?page=pages/perimeter/perimeter.php
2) Формула площади квадрата S=a2. Подробно читать здесь http://math-prosto.ru/?page=pages/area/area_figures.php
Приступим к решению. Выразим сторону квадрата из формулы периметра:
P=4a
a=P: 4
a= 280: 4 = 70 (см)
Теперь воспользуемся формулой площади квадрата:
S=a2
S=702=4900 (см2)
Ответ: площадь квадрата равна 4900 см2
0
Спасибо
Ответить
4 сентября 2015 в 15:44
Игорь Винников

Профиль
Благодарили: 0
Сообщений: 2

Игорь Винников
Профиль
Благодарили: 0
Сообщений: 2
Площадь прямоугольника64мс2, одна из сторон 16см. Надо найти соседнюю сторону
0
Спасибо
Ответить
1 сентября 2016 в 10:18
Ответ для Игорь Винников
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Площадь прямоугольника рассчитывается по формуле S=a · b. Подставим значения в формулу и вычислим вторую сторону:
64=16 · b
b=64/16=4
вторая сторона равна 4.
проверка: 16 · 4 = 64.
Ответ: Соседняя сторона прямоугольника равна 4 см.
0
Спасибо
Ответить
6 июля 2015 в 17:48
Дмитрий Рыжков

Профиль
Благодарили: 0
Сообщений: 2

Дмитрий Рыжков
Профиль
Благодарили: 0
Сообщений: 2
Посмотрите, у вас не первый раз перепутаны буквы в примерах.Например посмотрите нм тему: площадь сложных фигур.там же треугольник обозначен одними буквами, а написано в примере другими совершенно. Никто не ответил по предыдущей теме.спасибо.
0
Спасибо
Ответить
12 июля 2015 в 13:31
Ответ для Дмитрий Рыжков
Борис Гуров

Профиль
Благодарили: 1
Сообщений: 27

Борис Гуров
Профиль
Благодарили: 1
Сообщений: 27
Здравствуйте, Дмитрий.
Благодарим Вас за указанное замечание.
Пожалуйста, укажите, более конкретно место ошибки.
В уроке «Площадь сложных фигур» мы не нашли ошибку, о которой Вы написали.
0
Спасибо
Ответить
17 мая 2015 в 10:59
Соня Кизилова

Профиль
Благодарили: 0
Сообщений: 1

Соня Кизилова
Профиль
Благодарили: 0
Сообщений: 1
Самостоятельная работа.
Задание 3.
На сколько частей разбивают плоскость 4 прямые, пересекающиеся в одное точке?
Задание 2.
Начертите угол MON. Отметьте точку K, лежащую внутри этого угла, и точку L, лежащую на отрезке NK.
Задание 4.
Постройте треугольник ABC со стороной AB= 6см,?ABC= 45градусов, ?BAC= 75 градусов.Помогите пожалуйста![]() …
…
0
Спасибо
Ответить
17 мая 2015 в 12:57
Ответ для Соня Кизилова
Ярослава Фесенко

Профиль
Благодарили: 0
Сообщений: 3

Ярослава Фесенко
Профиль
Благодарили: 0
Сообщений: 3
1.8 частей
0
Спасибо
Ответить
- Главная
- Справочники
- Справочник по математике для начальной школы
- Основы геометрии
- Площадь фигуры
В этом разделе мы познакомимся с новым математическим понятием: с площадью фигуры.
Площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией
Ты знаешь другие понятия, которые тоже называют словом ПЛОЩАДЬ.
Например, площадь в городе – это чаще всего красивое место с клумбами, фонтаном и памятниками.

Посевная площадь – это участок земли, предназначенный для сельскохозяйственных целей.

Сравнение площадей фигур
При сравнении площади фигур, мы узнаём, больше или меньше места занимает данная фигура на плоскости.
Например, сравним площади двух фигур: треугольника и круга.

Мы видим, что площадь треугольника больше площади круга. Это видно на глаз, то есть первый способ сравнения площадей фигур: на глазок.
Сравнение площадей способом наложения
Иногда на глаз трудно определить, площадь какой фигуры больше. Давай сравним площади двух треугольников:

Совместим фигуры так, чтобы одна фигура полностью поместилась в другой.

Мы видим, что синий треугольник поместился в красном треугольнике, значит, площадь красного треугольника больше, чем площадь синего треугольника.
Сравнение площадей заданной меркой
Иногда нельзя определить, площадь какой фигуры больше способом наложения. Давай сравним площади двух фигур:

В таком случае измерять площади фигур будем заданной меркой, а потом сравним их.
Например, меркой может быть вот такой прямоугольник : 
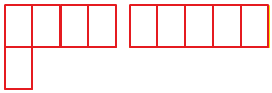
В первой фигуре поместилось 5 мерок, во второй фигуре поместилось 5 таких же мерок. Значит, площади фигур равны.
Единицы площади
В математике измерять площади фигур математики всего мира договорились одинаковыми мерками.
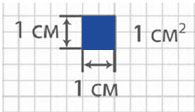
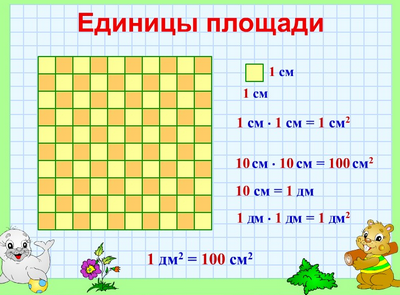
Квадратный сантиметр
Квадрат, сторона которого 1 см – это единица площади – квадратный сантиметр: см²
Определим площадь данных фигур:
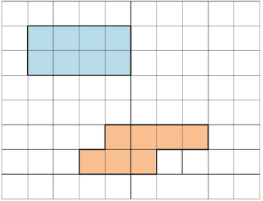
В синей фигуре 8 см², а в красной фигуре – 7 см².
8 > 7, значит, 8 см² > 7 см² а это значит, что площадь синей фигуры больше, чем площадь красной фигуры.
Квадратный дециметр
Квадрат, сторона которого 1 дм – это единица площади – квадратный дециметр: дм²
Вычислим, сколько квадратных сантиметров содержится в 1 квадратном дециметре:
1 дм² = ? см²
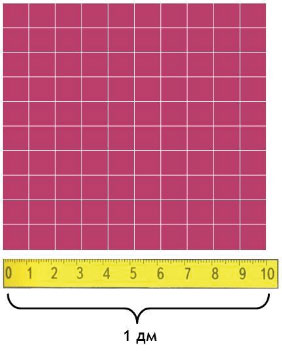
Сторона такого квадрата равна 10 см, а площадь квадрата равна произведению его сторон, то есть
10 • 10 = 100 см²
Значит, 1 дм² = 100 см²
Квадратный метр
Квадрат, сторона которого 1 м – это единица площади – квадратный метр: м²
Этой единицей мы пользуемся, когда хотим узнать площадь комнаты, класса, школьного двора или бабушкиного сада.
1 м² = 100 дм²
Квадратный километр
Квадрат, сторона которого 1 км – это единица площади – квадратный километр: км²
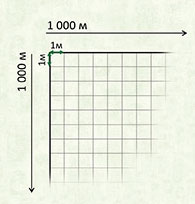
Этой единицей мы пользуемся, когда хотим узнать площадь города или страны. Например, площадь России составляет более семнадцати миллионов квадратных километров.
1 км² = 1000000 м²
Квадратный миллиметр
Квадрат, сторона которого 1 мм – это единица площади – квадратный миллиметр: мм²
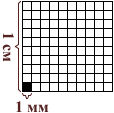
Этой единицей мы пользуемся для измерения очень маленьких площадей.
1 см² = 100 мм²
Длина и ширина клеточки школьной тетради по математике – пять миллиметров, значит там пять рядов по пять квадратных миллиметров. 5 • 5 = 25, поэтому в одной клеточке двадцать пять квадратных миллиметров.
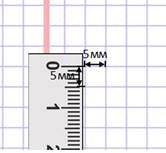
Для черчения и измерения фигур маленькой площади удобно использовать миллиметровую бумагу.
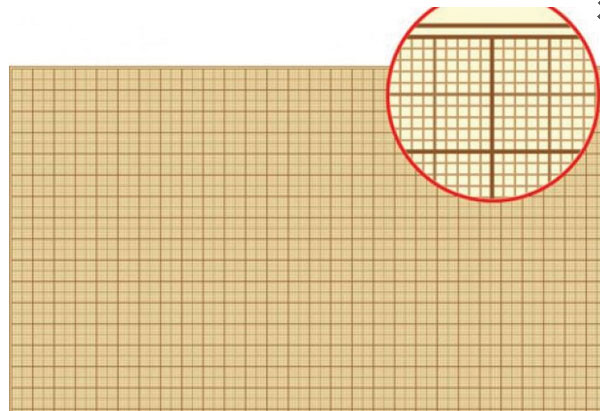
Ар
Ар – это площадь квадрата со стороной 10 м.
Слово “ар” при числах сокращённо записывают так:
1 а, 20 а, 97 а.
1 а2 = 100 м2, поэтому ар часто называют соткой.
Гектар
Гектар – это площадь квадрата со стороной 100 м.
Слово “гектар” при числах сокращённо записывают так:
1 га, 20 га, 530 га.
Чтобы перевести площадь из квадратных метров в гектары, необходимо число квадратных метров разделить на 10000.
Ар и гектар используются при измерении земельных участков.
Советуем посмотреть:
Площадь прямоугольника
Круг. Шар. Овал
Треугольники
Многоугольники
Угол. Виды углов
Обозначение геометрических фигур буквами
Периметр многоугольника
Окружность
Основы геометрии
Правило встречается в следующих упражнениях:
2 класс
Страница 44. Урок 17,
Петерсон, Учебник, часть 2
Страница 45. Урок 17,
Петерсон, Учебник, часть 2
Страница 50. Урок 19,
Петерсон, Учебник, часть 2
Страница 58. Урок 23,
Петерсон, Учебник, часть 2
Страница 61. Урок 24,
Петерсон, Учебник, часть 2
Страница 79. Урок 32,
Петерсон, Учебник, часть 2
Страница 85. Урок 35,
Петерсон, Учебник, часть 2
Страница 40. Урок 14,
Петерсон, Учебник, часть 3
Страница 47. Урок 16,
Петерсон, Учебник, часть 3
Страница 56. Урок 20,
Петерсон, Учебник, часть 3
3 класс
Страница 72. ПР 1. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 32,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 70,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 98,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 109,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 27. Урок 9,
Петерсон, Учебник, часть 1
Страница 84. Урок 30,
Петерсон, Учебник, часть 1
Страница 67. Урок 28,
Петерсон, Учебник, часть 2
Страница 37. Урок 17,
Петерсон, Учебник, часть 3
Страница 42. Урок 19,
Петерсон, Учебник, часть 3
4 класс
Страница 49,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 55,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 93,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 51,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 35. Тест 2. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 56,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 83,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 85,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 4,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 14,
Моро, Волкова, Рабочая тетрадь, часть 2
План урока:
Понятие площади фигур
Сравнение площадей фигур
Квадратный сантиметр, дециметр, метр
Площадь прямоугольника
Преобразование величин
Здравствуйте, друзья! Давайте познакомимся. Я — Сова — Мудрая голова.

Масса моего мозга больше, чем у других птиц. Я, как все учителя, терпелива, замечаю все вокруг, слышу шорохи, обдумываю свои шаги. У многих народов меня считают символом знаний.
Сегодня на уроке мы познакомимся с различными способами сравнения и измерения геометрических фигур, а я поделюсь с вами своей мудростью.
Будь внимателен, дружок!
Начинаем наш урок.
Понятие площади фигур
Распределите фигуры на группы.

Какие фигуры вы видите?
Прямые и кривые линии, прямые и кривые, овалы, круг, прямоугольники, квадраты, треугольники.
Чем похожи данные фигуры?
Их можно начертить на плоскости.
Чем они отличаются?
Из бумаги можно вырезать только плоские фигуры, у которых кроме длин сторон, можно вычислить и новую величину — площадь.
Для чего это надо нам знать? Когда может пригодиться?
Величины нужны не только для решения математических задач, но и в жизни. Чтобы сделать поделку, надо определить, какое количество бумаги потребуется. При ремонте квартиры мы считаем, сколько купить рулонов обоев, чтобы оклеить стены комнаты. Величина понадобится при постройке дома, при изготовлении какой-либо продукции в промышленности. Даже в саду и огороде хозяйки считают, хватит ли места на грядке.
Как можно объяснить слово площадь? Значение понятий мы узнаем в толковых словарях.
Прочитайте, какой смысл нового термина в словаре С.И. Ожегова.
Первое объяснение:

Как называется главное место столицы нашей страны?
Красная площадь в Москве.

Вторая формулировка:

Общую и полезную площадь имеют разные помещения:
Квартира, в которой вы живете.
Классная комната, где вы учитесь.
Спортивный зал, столовая, бассейн школы.
Разные объекты, занимающие место на земле, можно встретить в любом городе.

Игровая площадка

Строительная площадка
Интересно, что некоторые люди заводят дома ушастых сов. Но держать птиц в клетке не рекомендуется: для них требуется более просторная комната, где они могли бы летать.

Жилая площадь квартиры
Любым диким животным лучше жить на воле. Сова – это хищная птица. Она питается грызунами, мышами, полевками, насекомыми и птицами. В этом отношении колоссальная польза от совы состоит в том, что за одно лето она может уничтожить около одной тысячи полевых мышей. Каждый грызун уничтожает более килограмма зерна на посевных площадях страны.

Поле с зерновыми культурами
Понятие площади фигуры:

В математике говорят — площадь фигуры. Это величина пространства, ограниченного замкнутым контуром (периметром фигуры).
Ее можно посчитать математическими методами. С этой целью еще в далекой древности была создана целая наука под названием геометрия. Она применялась для деления поля на земельные участки, но потом ее стали использовать для измерения различных фигур. Поэтому их называют геометрическими фигурами, их место на плоскости — площадью.

Сравнение площадей фигур
Мы можем площади плоских фигур сравнить на глазок. Посмотрите на иллюстрацию.

Картина на стене занимает меньше места, потому говорят, что ее площадь меньше, чем стена. Книги, тетради меньше площади крышки стола. Их как бы наложили сверху, и еще осталось место.
Перечислите способы сравнения фигур по площади.
Можно сравнить на глазок или накладывая предметы, фигуры друг на друга.
Расставьте в порядке уменьшения:

Если получилось так: 3, 1, 2, 4, то вы отлично справились.
Теперь сравните треугольник с кругом:

Круг меньше площади треугольника.
Сравнить можно с помощью любых мерок. На рисунке прямоугольники измеряли заданной меркой — треугольником.

В левый прямоугольник их поместилось 18, а в правый — 20. Делаем вывод, что площадь левой фигуры меньше, чем правой.
Хороший способ сравнения — это подсчет клеток.
Чтобы сравнить площади клетчатых фигур, надо пересчитать количество клеток:

Фигура 3 самая маленькая по площади – 6 клеток. Фигура 2 имеют большую площадь, чем 3. В ней 7 клеток. Площади фигур 1,4,5,6 равновеликие. Они равны 8 клеткам, по площади больше фигур 2 и 3.
Разностное сравнение площадей фигур — это нахождение разницы между большей и меньшей величиной.
Сравните площади фигур 3 и 1. Запишите результаты сравнения.
Проверьте себя:
8 – 6 = 2
Ответ: 2 клетки
Квадратный сантиметр, дециметр, метр
Какой меркой лучше измерить площадь фигуры квадрата и прямоугольника?
В 18 веке на Руси вводилась основная мера измерения площади — десятина и четь. Но поля крестьян были неровными, поэтому часто мерками служила урожайная копна. Народ изобретал особые мерки: выть, соха, обжа, коробь, веревка, жеребья. Сейчас мы не используем этих мер.

Начертите прямоугольник со сторонами 5см и 4см. Какими мерками можно измерить фигуру?

Посмотрите на рисунок, утенок измерил прямоугольник с помощью треугольников, ежонок — квадратами, а котенок — прямоугольниками.

Посчитаем, сколько единичных мерок находится в прямоугольнике. У животных получились разные величины: 40, 20, 10.
Всегда ли удобно определять площадь фигуры произвольными мерками?
Конечно, нет.
Вывод: значение величины зависит от выбранной мерки. Чтобы сравнить, нужно договориться об одинаковом способе измерения.
Всегда ли для определения площади фигуры подходит клетка?
Да.
Какого размера должна быть клетка?
Я предлагаю измерять как ежик, квадратами по 2 клеточки.
Измерьте длину и ширину этого квадратика. Что получилось?

Длина и ширина равна 1 см.
Единицей измерения площади еще 4-5 тысяч лет тому назад жители древнего города Вавилона считали квадрат, так как именно квадрат имеет превосходные признаки: четыре стороны равны межу собой, четыре прямых угла; можно провести ось и найти центр симметрии. Форма квадрата без изъянов, совершенна, поэтому его легко начертить и плотно покрыть фигуры любой формы.
Если у квадратика сторона 1см – площадь его равна квадратному сантиметру.
1 квадратный сантиметр сравним с ноготком взрослого человека.

Записывается площадь 1 квадратного сантиметра так:
S = 1 кв. см или S = 1 см2
Латинская буква «эс» обозначает площадь, двойка в правом верхнем углу — две величины: длину и ширину.
Начертите квадрат со стороной 10 сантиметров.

Квадратный дециметр (1 дм 2) — это квадрат со стороной 1 дм или 10 см.

Квадратный метр (1 м 2) — это квадрат со стороной 1 м или 10 дм. В квадратных метрах обозначается площадь в жилых помещениях, например: в комнатах, коридорах. Эта мерка подойдет для измерения дачного участка, спортивного зала, территории сквера.

А при строительстве школ важно учитывать, сколько квадратных метров должно быть в классе, если для одного ученика по санитарным правилам нужно 4 квадратных метра.
Вы хорошо справляетесь с заданиями. Спине, голове, всему телу нужен отдых. Встаньте на физкультурную минутку.
Физкультминутка
Поднимитесь, вверх потянитесь,
Вперед наклонитесь.
Ниже, ниже тянитесь,
Достаньте мизинцем до пятки.
Получилось? Тогда все в порядке.
Выпрямитесь, грудью вздохните,
Руки шире в стороны разведите.
Соедините в замок на лопатках.
Получилось? Тогда все в порядке.
Глазки зажмурьте, спокойно постойте.
Отдохнули? Теперь посчитайте площадки.
Площадь прямоугольника
Площади простых фигур, таких как квадратов и прямоугольников рассчитывать научились быстро. Для этого измеряют стороны прямоугольника.
Площадь прямоугольника находится по формуле: S = a ∙ b, где длину надо умножить на ширину фигуры.
Задание 1.
Постройте прямоугольник, длина которого 50 мм, а ширина 30 мм.

Можно ли длину и ширину данного прямоугольника выразить в сантиметрах?
Можно.
|
50 мм = 5 см |
30 мм = 3 см |
Найдите периметр прямоугольника. Р = (a + b) ∙ 2
Р = (5 + 3) ∙ 2 = 16 (см)
Ответ: 16 см
Имеет ли построенная вами фигура площадь?
Да. Прямоугольник имеет длину 5 см и ширину 3 см. Найдем, чему равна площадь прямоугольника по формуле S = a ∙ b.
S = 5 ∙ 3 = 15 см2
Ответ: площадь прямоугольника равна 15 кв.см.
Задание 2.
Чему равна площадь прямоугольника со сторонами 5 см и 4 см? Рассуждаем так. Нам известна длина и ширина прямоугольника. Площадь равна произведению этих величин.
S = 5 ∙ 4 = 20 см2
Ответ: 20 кв.см.
Задание 3.
Рассмотрите следующий рисунок:

Как называется данная геометрическая фигура?
Многоугольник.
Как найти площадь этого многоугольника?
Найти площади отдельных прямоугольников.
Найдите площадь этого многоугольника разными способами.
Первый способ.

Решение.
Измеряем стороны большого прямоугольника.
Длина равна 3 см, а ширина 3 + 1 = 4 (см).
1) 4 · 3 = 12 (см2) – площадь большого прямоугольника.
Длина маленького прямоугольника 3 см, а ширина 1 см. Перемножим эти величины.
2) 3 · 1 = 3 (см2) – площадь маленького прямоугольника.
Теперь из большей фигуры вырезаем два маленьких белых прямоугольника.
3) S = 12 – 3 – 3 = 6 (см2) – площадь многоугольника.
Второй способ.

Решение.
1) 3 · 1 = 3 (см2) – площадь верхнего прямоугольника.
2) 3 · 1 = 3 (см2) – площадь второго прямоугольника.
3) S = 3 + 3 = 6 (см2) – общая площадь многоугольника.
Ответ: S = 6 см2
Преобразование величин
По формуле S = a ∙ b квадратные сантиметры можно выразить в квадратных метрах. Давайте вспомним, что один метр равен сто сантиметрам.
1 м = 100 см
Мы выполним умножение сторон, и найдем квадратную величину.
Значит: 1 м2 = 100 ∙ 100 = 10000 см2
Задание 4.
Вычислите сколько кв.дм в 1 м2. Во сколько раз 1 кв. м. больше 1 кв. дм?
Как преобразовать квадратные дециметры в квадратные метры? Давайте рассуждать так. Квадрат со стороной 1 м разделим на 10 столбиков. В каждом таком столбике по 10 кв. дм, то есть всего в кв. м 10 десятков, или 100 дм2.

Второй вариант размышлений отталкивается от формулы. Умножаем длину на ширину. 10 дм на 10 дм, получится 100 дм2.
1 м2 = 10 ∙ 10 = 100 дм2
Ответ: в 1 кв. м содержится 100 кв.дм. 1 кв.м. в сто раз больше одного квадратного дециметра.
Задание 5.
Сколько кв. см в 1 кв. дм? Во сколько раз 1 кв. дм. больше 1 кв. см?
Выражаем квадратные дециметры в квадратных сантиметрах.
1 дм = 10 см
1 дм2 = 10 ∙ 10 = 100 см2
Ответ: 1 кв.дм равен 100 кв.см. 1 кв.дм в сто раз больше одного квадратного сантиметра.
Выполните упражнение:
Найдите, сколько квадратных дециметров в 8 м2, в 25 м2, в 45 м2 9 дм2
Мы знаем, что 1 м2 – это 100 дм2, то есть число м2 в 100 раз больше числа дм2, поэтому умножим 8 на 100, получим 800 дм2.
25 м2 : умножим 25 на 100 = 2500 дм2.
45 м2 9 дм2 : это 45 ∙ 100 + 9 = 3100 + 9 = 4509 мм2.
Наш урок подходит к концу.
Продолжите фразу:
сегодня я научился
было интересно
было трудно
Вы хорошо потрудились, поэтому сможете справиться с самостоятельными заданиями.
До новых встреч!
Как найти квадратные сантиметры
Квадратные сантиметры – это метрическая единица измерения площади различных плоских геометрических фигур. Она имеет повсеместное применение, начиная со школьной скамьи и кончая вычислениями на уровне архитектуры и механики. Найти квадратные сантиметры не очень трудно

Инструкция
Квадратный сантиметр образно представляет собой квадрат, у которого длина стороны составляет 1 см. Треугольники, прямоугольники, ромбы и другие геометрические фигуры могут включить в себя далеко не один такой квадрат. Таким образом, квадратный сантиметр, по своей сути, является одной из самых часто применяемых единиц измерения площади фигур в школьной программе.
Площади различных плоских геометрических фигур вычисляется по разному:
S = a² – это площадь квадрата, где a – длина любой из его сторон;
S = a*b – площадь прямоугольника, где a и b – стороны данной фигуры;
S = (a*b*sinα)/2 – площадь треугольника, a и b – стороны данного треугольника,α – угол между данными сторонами. На самом деле, формул для исчисления площади треугольника чрезвычайно много;
S = ((a + b)*h)/2 – площадь трапеции, a и b – основания трапеции, h – ее высота. Формул по вычислению площади трапеции также существует несколько;
S = a*h – площадь параллелограмма, а – сторона параллелограмма, h – проведенная к данной стороне высота.
Приведенные выше формулы – далеко не все, с помощью которых можно вычислить площади различных геометрических фигур.
Для того, чтобы было понятнее, как найти квадратные сантиметры, можно привести несколько примеров:
Пример 1: Дан квадрат, у которого длина стороны составляет 14 см, необходимо вычислить ее площадь.
Решить задачу можно при помощи одной из данных выше формул:
S = 14² = 196 см²
Ответ: площадь квадрата составляет 196 см²
Пример 2: Имеется прямоугольник, длина которого 20 см, а ширина 15 см, опять же требуется найти его площадь. Решить поставленную задачу можно при помощи второй формулы:
S = 20*15 = 300 см²
Ответ: площадь прямоугольника 300 см²
Если же в задаче единицами измерения сторон и других частей фигуры являются не сантиметры, а, к примеру, метры или дециметры, то выразить площадь данной фигуры в сантиметрах опять же очень легко.
Пример 3: Пусть дана трапеция, основания которой равны 14 м и 16 м, высота ее 11 м. Требуется вычислить площадь фигуры. Для этого придется воспользоваться четвертой формулой:
S = ((14+16)*11)/2 = 165 м² = 16500 см² (1 м = 100 см)
Ответ: площадь трапеции 16500 см²
Источники:
- квадратный сантиметр
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
