Как найти площадь фигуры задачи 5 класс

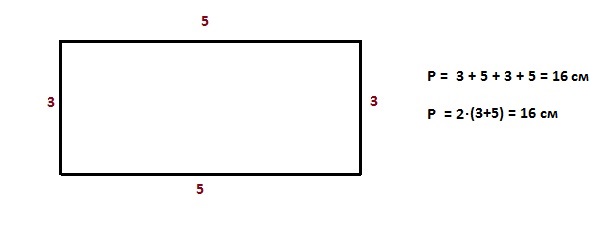
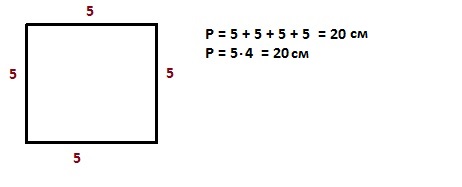
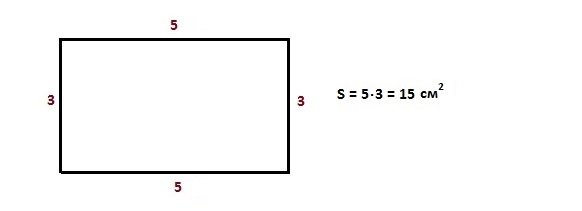
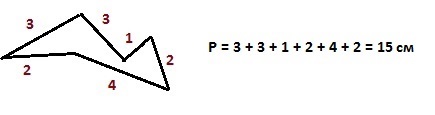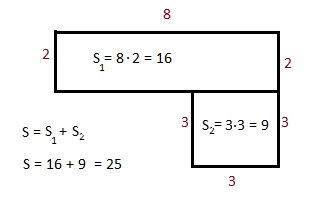На мой взгляд, задача учителя – не только научить, а развить познавательный интерес у учащегося. Поэтому, когда возможно, связываю темы урока с практическими задачами.

На занятии учащиеся под руководством учителя составляют план решения задач на нахождение площади «сложной фигуры» (для расчеты сметы ремонта), закрепляют навыки решения задач на нахождение площади; происходит развитие внимания, способности к исследовательской деятельности, воспитание активности, самостоятельности.

Работа в парах создает ситуацию общения между теми, кто имеет знания и теми, кто их приобретает; в основе такой работы лежит повышение качества подготовки по предмету. Способствует развитию интереса к процессу учения и более глубокому усвоению учебного материала.

Урок не только систематизирует знания обучающихся, но и способствует развитию творческих, аналитических способностей. Применение задач с практическим содержанием на уроке позволяет показать востребованность математических знаний в повседневной жизни.

Цели урока:

Образовательные:

• закрепление знаний формул площади прямоугольника, прямоугольного треугольника;
• анализ заданий на вычисление площади “сложной” фигуры и способов их выполнения;
• самостоятельное выполнение заданий для проверки знаний, умений, навыков.

Развивающие:

• развитие приёмов умственной и исследовательской деятельности;
• развитие умения слушать и объяснять ход решения.

Воспитательные:

• воспитывать у учащихся навыки учебного труда;
• воспитывать культуру устной и письменной математической речи;
• воспитывать дружеское отношение в классе и умение работать в группах.

Тип урока: комбинированный.

Оборудование:

• Математика: учебник для 5 кл. общеобразоват. учреждений/ Н.Я. Виленкин, В.И. Жохов и др., М.: «Мнемозина», 2010.
• Карточки для групп учащихся с фигурами для вычисления площади сложной фигуры.
• Чертёжные инструменты.

План урока:

1. Организационный момент.
2. Актуализация знаний.
   а) Теоретические вопросы (тест).
   б) Постановка проблемы.
3. Изученного нового материала.
   а) поиск решения проблемы;
   б) решение поставленной проблемы.
4. Закрепление материала.
   а) коллективное решение задач;
   Физкультминутка.
   б) самостоятельная работа.
5. Домашнее задание.
6. Итог урока. Рефлексия.

Ход урока

I. Организационный момент.

Урок мы начнём вот с таких напутствующих слов:

Математика, друзья,
Абсолютно всем нужна.
На уроке работай старательно,
И успех тебя ждёт обязательно!

II. Актуализация знаний.

а) Фронтальная работа с сигнальными карточками (у каждого ученика карточки с числами 1, 2, 3, 4; при ответе на вопрос теста ученик поднимает карточку с номером правильного ответа).

1. Квадратный сантиметр – это:

1. площадь квадрата со стороной 1 см;
2. квадрат со стороной 1 см;
3. квадрат с периметром 1 см.

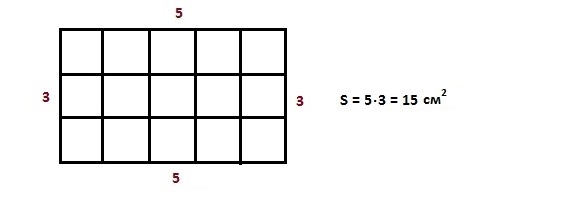
2. Площадь фигуры, изображённой на рисунке, равна:

1. 8 дм;
2. 8 дм²;
3. 15 дм².

3. Справедливо ли утверждение, что равные фигуры имеют равные периметры и равные площади?

1. да;
2. нет.

4. Площадь прямоугольника определяется по формуле:

1. S = a²;
2. S = 2 • (a + b);
3. S = a • b.

5. Площадь фигуры изображённой на рисунке, равна:

1. 12 см;
2. 8 см;
3. 16 см.

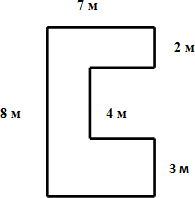
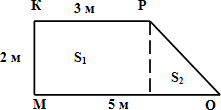
б) (Постановка проблемы). Задача. Сколько надо краски, чтобы покрасить пол, который имеет следующую форму (см. рис.), если на 1 м² расходуется 200 г краски?

III. Изучение нового материала.

Что же мы должны узнать, чтобы решить последнюю задачу? (Найти площадь пола, который имеет вид «сложной фигуры».)

Учащиеся формулируют тему и цели урока (если необходимо учитель помогает).

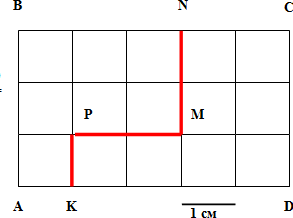
Рассмотрим прямоугольник ABCD. Проведём в нем линию KPMN, разбив прямоугольник ABCD на две части: ABNMPK и KPMNCD.

Чему равна площадь ABCD? (15 см²)

Чему равна площадь фигуры ABMNPK? (7 см²)

Чему равна площадь фигуры KPMNCD? (8 см²)

Проанализируйте полученные результаты. (15= = 7 + 8)

Вывод? (Площадь всей фигуры равна сумме площадей её частей.)

S = S₁ + S₂

Как можно применить это свойство для решения нашей задачи?(Разобьём сложную фигуру на части, найдём площади частей, затем площадь всей фигуры.)

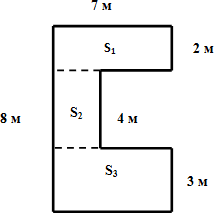
S₁ = 7 • 2 = 14 (м²)
S₂ = (7 – 4) • (8 – 2 – 3) = 3 • 3 = 9 (м²)
S₃ = 7 • 3 = 21 (м²)
S = S₁ + S₂ + S₃ = 14 + 9 + 21 = 44 (м²)

Давайте составим план решения задач на нахождение площади «сложной фигуры»:

1. Разбиваем фигуру на простые фигуры.
2. Находим площади простых фигур.

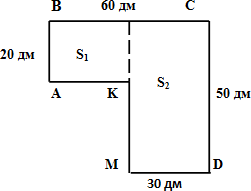
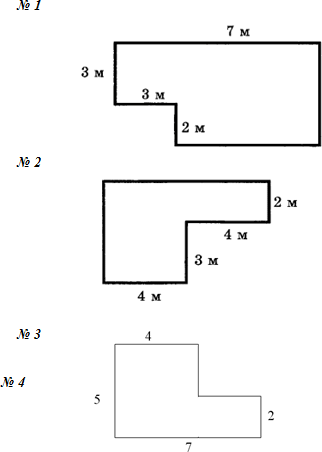
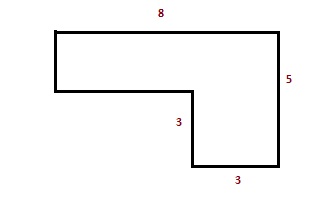
а) Задача 1. (коллективное решение на доске и в тетрадях.) Сколько потребуется плитки, чтобы выложить площадку следующих размеров:

Решение:

S = S₁ + S₂
S₁ = (60 – 30) • 20 = 600 (дм²)
S₂ = 30 • 50 = 1500 (дм²)
S = 600 + 1500 = 2100 (дм²)

Есть ли другой способ решения? (Рассматриваем предложенные варианты.)

Ответ: 2100 дм².

Задача 2. (коллективное решение на доске и в тетрадях.) Сколько требуется м² линолеума для ремонта комнаты, имеющей следующую форму:

Решение:

S = S₁ + S₂
S₁ = 3 • 2 = 6 (м²)
S₂ = ((5 – 3) • 2) : 2 = 2 (м²)
S = 6 + 2 = 8 (м²)

Ответ: 8 м².

Физкультминутка.

А теперь, ребята, встали.
Быстро руки вверх подняли.
В стороны, вперед, назад.
Повернулись вправо, влево.
Тихо сели, вновь за дело.

б) Самостоятельная работа (обучающего характера).

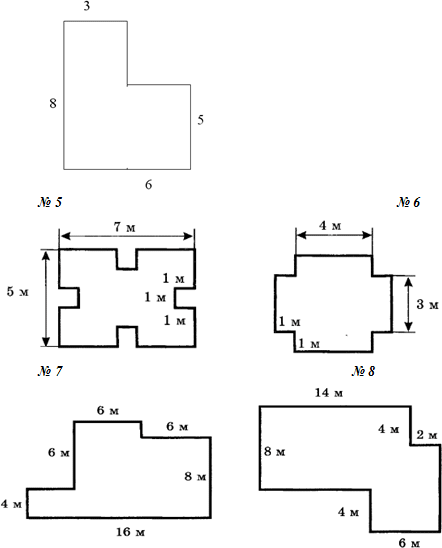
Учащиеся разбиваются на группы (№ 5–8 более сильные). Каждая группа – ремонтная бригада.

Задание бригадам: определите, сколько надо краски, чтобы покрасить пол, имеющий форму фигуры, изображённой на карточке, если на 1 м² требуется 200 г краски.

Вы эту фигуру строите своей тетради и записывая все данные, приступаете к выполнению задания. Можете обсуждать решение (но только в своей группе!). Если какая-то группа справляется с заданием быстро, то ей – дополнительное задание (после проверки самостоятельной работы).

Задания для групп:

V. Домашнее задание.

п. 18, № 718, № 749.

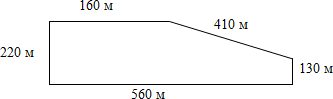
Дополнительное задание. План-схема Летнего сада (Санкт-Петербург). Вычислить его площадь.

VI. Итоги урока.

Рефлексия. Продолжи фразу:

• Сегодня я узнал…
• Было интересно…
• Было трудно…
• Теперь я могу…
• Урок дал мне для жизни…

Инфоурок

›

Математика

›Другие методич. материалы›Урок по теме “Площадь сложной фигуры” (5 класс)

Математика

5 класс

Урок №30

Площадь прямоугольника. Единицы площади

Перечень рассматриваемых вопросов:

– понятие площади фигуры;

-единицы измерения площади; 

– площадь прямоугольника, квадрата; 

– приближенное измерение площади фигуры на клетчатой бумаге.

Тезаурус

Прямоугольник – четырёхугольник, у которого все углы прямые (равны 90 градусам). 

Квадрат – прямоугольник, у которого все стороны равны. 

Площадь прямоугольника– число, которое показывает, сколько квадратных единиц содержится в прямоугольнике.

Основная литература

Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений.// С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

Дополнительная литература

1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы.// И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

Сегодня мы начнём занятие с задачи. Представим, что две девочки пришли в магазин, чтобы купить в подарок подруге на день рождения коробку конфет. На витрине были разложены самые разные наборы сладостей. Девочки решили купить ту коробку, которая больше. А какая из них больше? Как это измерить? Можно сравнить коробки по длине и ширине или просто положить их друг на друга. Но одна коробка оказалась длиннее, а другая – шире. Какая же из них больше? Как это узнать?

Чтобы ответить на эти вопросы, мы поговорим о вычислении площади прямоугольника.

Для начала введём понятие площади фигуры.

Если какую-нибудь площадь можно разбить на n квадратов со стороной, например, 1 см, то получится, что площадь фигуры равна n см².

За единицу измерения площадей принимают не только квадратный сантиметр, но и квадратный миллиметр, квадратный дециметр, квадратный метр.

Это площади квадратов, длины сторон которых равны одному миллиметру, одному дециметру и одному метру соответственно.

Далее покажем, что подразумевается под площадью прямоугольника.

Площадью прямоугольника называют число, которое показывает, сколько квадратных единиц содержится в прямоугольнике.

Называя величину площади, необходимо указывать единицу измерения.

Например, прямоугольник состоит из пятнадцати квадратов; площадь каждого квадрата составляет 1 см². Следовательно, площадь всего прямоугольника равна 15 см².

S = 15 см²

Решим задачу.

Найдём площадь прямоугольника ABCD, который имеет длину АВ = 6 см и ширину ВС = 7 см. Для этого разделим его на квадратные сантиметры. Сосчитаем, сколько квадратных сантиметров в нём содержится.

В прямоугольнике ABCD квадратный сантиметр содержится сорок два раза – значит, его площадь равна: S = 42 см² = 6 см · 7 см = АВ · ВС.

Поэтому можно ввести формулу для нахождения площади прямоугольника.

Чтобы найти площадь прямоугольника S, нужно умножить его длину a на ширину b.

S = а · b

Так как квадрат является прямоугольником, у которого все стороны равны, то его площадь можно вычислить как квадрат его стороны а.

S = а · а = а²

Далее найдём соотношение между единицами измерения площадей.

Так как 1 см = 10 мм, следовательно, 1 см² = 10² мм² = 100 мм².

Соответственно, 1 дм² = 10² см² = 100 см²

1 м² = 10² дм² = 100 дм²

1 км² = 1000² м² = 1000000 м².

Для измерения небольших площадей земельных участков используют специальную единицу измерения– ар, которая равна площади квадрата со стороной десять метров. В обиходе ар называют соткой, так как один ар– это сто квадратных метров.

1 ар = 10² м² = 100 м²

Для обмера больших земельных территорий ввели единицу один гектар, которая соответствует площади квадрата со стороной сто метров.

1 га = 100² м² = 10000 м² = 100 а

Решим задачу.

Найдём площадь прямоугольника.

При измерении окажется, что стороны с недостатком приближенно равны трём и пяти сантиметрам. Значит, площадь прямоугольника больше, чем произведение этих сторон, то есть пятнадцати квадратных сантиметров.

S (с недостатком) = 3 · 5 = 15 см²

Если взять стороны в приближении с избытком, то есть четыре и шесть сантиметров, то площадь будет меньше произведения сторон, а именно равна двадцати четырём квадратным сантиметрам.

S (с избытком) = 4 · 6 = 24 см²

Таким образом, площадь этого прямоугольника варьируется от пятнадцати до двадцати четырёх квадратных сантиметров.

15 см² < S < 24 см²

Отметим, что равные прямоугольники имеют равную площадь.

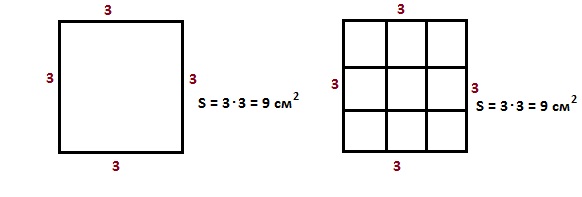
Сравним площади закрашенных квадратов, изображённых на рисунке.

Решение: если посмотреть внимательно на рисунок, то можно заметить, что все фигуры расположены в одинаковых квадратах со стороной 9 клеток, следовательно, площади этих квадратов одинаковы. На верхнем рисунке шесть фигур – два квадрата и четыре треугольника. На нижнем рисунке пять фигур – квадрат и четыре треугольника.

Далее внимательно посмотрим на треугольники – все они одинаковы, следовательно, их площади одинаковы. И, если из больших квадратов, в которых расположены наши фигуры, мы отнимем сумму площадей равных треугольников, получится, что площади оставшихся фигур (квадратов) верхней и нижней части равны.

Примеры заданий из Тренировочного модуля

№ 1. В квадрате все стороны равны 5 см. Чему равна площадь квадрата?

Решение: Для нахождения площади квадрата воспользуемся следующей формулой:

S = а² = 5см · 5 см = 25 см²

№ 2. Найдите площадь фигуры.

Решение: сначала следует разделить фигуру на три прямоугольника, далее найти площадь каждого по формулеS=а · b, а затем сложить площади трёх фигур. Или можно найти площадь прямоугольника со сторонами 10 см и 3 см, она равна 30 см². Далее вычислить площадь вырезанной фигуры со сторонами 2см на 1 см, она составляет 2см². И вычесть 2 см² из 30см².

Ответ: 28 см².

Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.

Площади равных фигур равны. Их периметры тоже равны.

Площадь квадрата

Пример:

S_EKFM = EK · EK

S_EKFM = 3 · 3 = 9 см²

Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:

S = a²

Площадь прямоугольника

Пример:

S_ABCD = AB · BC

S_ABCD = 3 · 7 = 21 см²

Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.

Площадь сложных фигур

Задача: найти площадь огородного участка.

Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.

Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

S_ABCE = AB · BC
S_EFKL = 10 · 3 = 30 м²
S_CDEF = FC · CD
S_CDEF = 7 · 5 = 35 м²

Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = S_ABCE + S_EFKL
S = 30 + 35 = 65 м²

Ответ: S = 65 м² — площадь огородного участка.

---

Свойство ниже может вам пригодиться при решении задач на площадь.

Рассмотрим прямоугольник:

АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников

ABC и
ACD

Вначале найдём площадь прямоугольника по формуле.

S_ABCD = AB · BC
S_ABCD = 5 · 4 = 20 см²

S
_ABC = S_ABCD : 2

S
_ABC = 20 : 2 = 10 см²

S
_ABC =
S
_ACD = 10 см²

---

Ваши комментарии

Оставить комментарий:

---

ПЕРИМЕТР

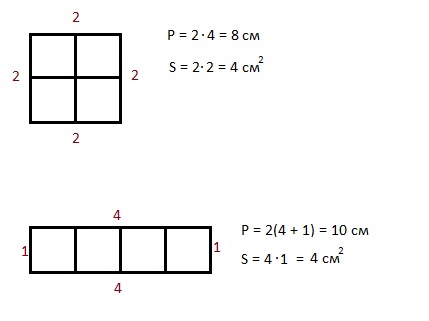
Периметр – сумма длин всех сторон плоской геометрической фигуры. Чаще всего периметр измеряется в сантиметрах, метрах и километрах.

Чаще всего периметр обозначается буквой P.

Периметр прямоугольника – удвоенная сумма длины и высоты – 2∙(a+b)

Периметр квадрата – произведение любой его стороны на 4, так как стороны равны.

ПЛОЩАДЬ

Площадь – характеристика замкнутой геометрической фигуры, которая показывает ее размер. Чаще всего площадь измеряется в квадратных сантиметрах, квадратных метрах и квадратных километрах.

В отличие от периметра, не существует универсальной формулы площади. Для каждого типа фигур площадь вычисляется по своей особой формуле. Мы будем рассматривать только прямоугольники, квадраты и составные фигуры из прямоугольников и квадратов.

Чаще всего площадь обозначается буквой S.

Площадь прямоугольника – произведение длины на высоту.

Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС

Разделим этот прямоугольник на квадраты

Мы получили 15 квадратов внутри этого прямоугольника – это и есть те самые 15 квадратных сантиметров, которые составляют площадь прямоугольника.

Площадь квадрата – произведение длины стороны на саму себя.

СОСТАВНЫЕ ФИГУРЫ

Разделим эту фигуру на прямоугольник и квадрат

Высота прямоугольника составит 5 – 3 = 2

СООТНОШЕНИЕ ПЛОЩАДИ И ПЕРИМЕТРА

Фигуры с одной и той же площадью могут иметь разный периметр

Почему у нас изменился периметр, хотя площадь, т.е. число квадратиков внутри фигуры, осталась прежней?

Потому что изменилось число граней квадратиков, которые участвуют в формировании сторон фигуры, т.е. перметра. В первой фигуре – большом квадрате, в формировании сторон участвовали по две внешних грани каждого маленького квадратика – общее число таких граней 8, и периметр равен 8.

Во второй фигуре у нас в формировании сторон участвуют по три грани у двух крайних квадратиков и по две грани внутренних квадратов. Общее число таких граней 10, и периметр равен 10.

ОБЪЁМ

Объём – количественная характеристика пространства, занимаемого телом или веществом. Чаще всего объём измеряется в кубических сантиметрах, кубических дециметрах, кубических метрах и литрах.

1 л = 1 дм³

Не существует универсальной формулы объема. Для каждого типа фигур объём вычисляется по своей особой формуле. Мы будем рассматривать только прямоугольные параллелепипеды.

Чаще всего объём обозначается буквой V.

Прямоугольный параллелепипед – замкнутая фигура, у которой 6 прямоугольных граней (передняя, задняя, нижняя, верхняя и две боковые), и каждая из граней расположены под прямым углом к соседним.

Объём прямоугольного параллелепипеда – произведение его длины, ширины и высоты

Зная объём и две стороны, мы можем найти третью сторону:

c = (V:a):b = V:S

ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.

ЗАДАЧИ

Задача 1. Найдите периметр и площадь прямоугольника, у которого ширина 10 см, и она меньше длины на 6 см.

x = 10 см – ширина

1. Найдём длину

y = 10 + 6 = 16 см

2. Найдём периметр

P = 2∙(10+16) = 52 см

3. Найдём площадь

S = 10∙16 = 160 см²

Ответ: P = 52 см, S = 160 см²

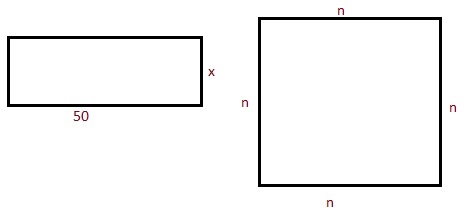
Задача 2. Какую ширину имеет прямоугольник, длина которого 50 см, а площадь совпадает с площадью квадрата периметром 80 см?

1. Вычислим сторону квадрата

4∙n = 80 – периметр

n = 20 см

2. Вычислим площадь квадрата

20∙20 = 400 см²

3. Вычислим ширину прямоугольника

50∙x = 400 см²

x = 8 см

Ответ: 8 см

Задача 3. Чему равна ширина прямоугольника, длина которого равна 15 м, а площадь 7500 дм2 ?

1 дм = 10 см, 1 м = 100 см, 1 м = 10 дм

1. Переведём длину прямоугольника в дм

x = 15∙10 = 150 дм

2. Найдём ширину прямоугольника

150∙y = 7500

y = 7500:150 = 50 дм

Ответ: 50 дм

Задача 4. Длина прямоугольника равна 60 см, и она в 3 раза больше ширины стороны.

1. Найдите площадь этого прямоугольника.

2. Найдите площадь квадрата, который имеет такой же периметр, как и прямоугольник.

3. Найдите периметр квадрата, площадь которого в 12 раз меньше площади прямоугольника.

1. Найдём ширину прямоугольника

x = 60:3 = 20 см

2. Найдём площадь прямоугольника

S = 60∙20 = 1200 см

2. Найдём периметр прямоугольника

P = 2∙(60+20) = 160 см

3. Найдём сторону квадрата

y = 160:4 = 40 см

4. Найдём площадь квадрата

Sкв = 40∙40 = 1600 см²

5. Найдём площадь квадрата, которая в 12 раз меньше площади прямоугольника:

Sкв₂ = 1200:12 = 100 см²

6. Найдём сторону такого квадрата

Площадь квадрата = 100 см²

Из таблицы умножения мы знаем, что 10∙10 = 100, значит сторона квадрата = 10 см

7. Найдём периметр такого квадрата

P = 10∙4 = 40 см

ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.

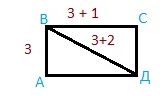
Задача 5. В прямоугольнике АВСД сторона АВ 3 см, сторона ВС на 1 см длиннее, а диагональ ВД на 2 см длиннее АВ. Найдите периметр и площадь прямоугольника АВСД и треугольника АВД.

1. Найдём сторону ВС

ВС = 3+1 = 4

2. Найдём диагональ ВД

ВД = 3+2 = 5

3. Найдём периметр АВСД

P = 2∙(3+4) = 14 см

4. Найдём площадь АВСД

Sавсд = 3∙4 = 12 см²

5. Найдём периметр треугольника АВД

Pавд = 3 + 5 + 4 = 13 см

6. Найдём площадь треугольника АВД

Треугольник АВД занимает половину площади прямоугольника АВСД

Sавд = Sавсд:2

Sавд = 12:2 = 6 см²

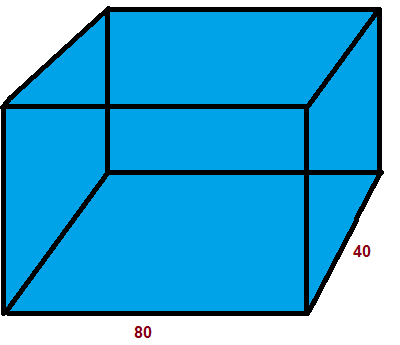
Задача 6. В аквариум в форме прямоугольного параллелепипеда, основание которого имеет стороны 80 и 40 см, налили до краёв 160 л. воды. Какова высота аквариума?

Решение

1. Переведём литры в кубические дециметры

1 л = 1 дм³, 160 л = 160 дм³

2. Переведём стороны аквариума в дециметры

1 дм = 10 см, 80 см = 8 дм, 40 см = 4 дм

3. Найдём высоту аквариума

V = a∙b∙c, a = 8, b = 4

c = (V:a):b

c = (160:8):4 = 5 дм

c = 5∙10 = 50 см

Ответ: 50 см