Геометрический смысл интеграла от функции f(x) в пределах от a до b – это площадь фигуры, ограниченной линиями:
y= f(x)
y = 0
x = a
x = b
Теперь нарисуйте в декартовой системе координат график функции у=2х, линии х=2, х=6. Посмотрите – получился четырехугольник, состоящий из пересекающихся линий у=2х, х=2, х=6 и оси Оу. Его площадь равна интегралу:
Integral(2x)dx в пределах от х=2 до х=6.
Теперь нарисуйте в той же декартовой системе координат, где нарисован предыдущий четырехугольник, аналогично предыдущему, четырехугольник, состоящий из пересекающихся линий у=5х, х=2 и х=6 и оси Оу. Его площадь будет равна интегралу:
Integral(5x)dx в пределах от х=2 до х=6.
А теперь посмотрите на рисунок! Заштрихуйте второй четырехугольник косой штриховкой, затем первый обратной штриховкой (первый получится заштрихованным в клеточку) . Четырехугольник, площадь которого Вы ищете получится заштрихованным косой штриховкой. А теперь сами догадайтесь, чему равна его площадь, если Вы знаете площадь первого и второго четырехугольников?
Удачи!
Вычислить площадь фигуры, ограниченной линиями
Данный калькулятор поможет найти площадь фигуры, ограниченной линиями.
Для того чтобы вычислить площадь фигуры, ограниченной линиями, применяется одно из свойств интеграла. Это свойство аддитивности площадей, интегрируемых на одном и том же отрезке функции.
Аддитивность означает, что площадь замкнутой области, составленных из нескольких фигур, не имеющих общих внутренних точек, равна сумме площадей этих фигур. Интеграл равен площади криволинейной трапеции, ограниченной графиками функций. Вычисление интеграла производится по закону Ньютона-Лейбница, согласно которому результат равен разности первообразной функции от граничных значений интервала.
Калькулятор поможет вычислить площадь фигуры ограниченной линиями онлайн.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Перейти к содержанию
Площадь криволинейной трапеции, ограниченной линиями
На чтение 2 мин. Просмотров 2.8k.
Как найти площадь криволинейной трапеции ограниченной прямыми? Для этого нам потребуется определенный интеграл с заданными границами.
В алгебре часто решаются задачи на нахождение площади криволинейной трапеции, заключенной между двумя кривыми. В задачах обычно спрашивают как найти площадь криволинейной трапеции ограниченной прямыми или как вычислить площадь фигуры, ограниченной линиями. Вычисление площадей криволинейных трапеций изучается в курсе алгебры в 11 классе.
Криволинейная трапеция — это условное название фигур — областей, которые образуются графиком кривой и линиями ограничивающими график с двух сторон.
Различают два случая:
- Переменная интегрирования х;
- Переменная интегрирования у.
Рассмотрим оба этих случая.
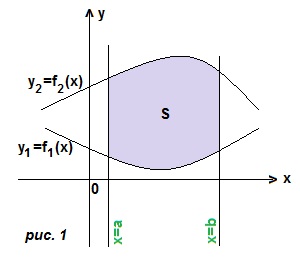
1) переменная интегрирования х. В этом случае трапеция ограничена сверху и снизу двумя кривыми, а слева и справа прямыми х=а, х=b. (рис. 1). Границы интегрирования a и b, а чтобы получить подынтегральную функцию, мы из уравнения верхней линии вычитаем уравнение нижней линии. Тогда площадь трапеции:
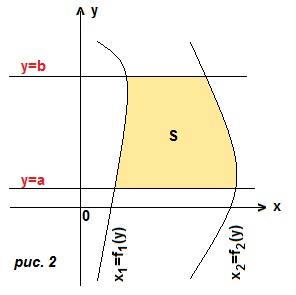
2) переменная интегрирования у. Криволинейная трапеция ограничена справа и слева двумя кривыми, а снизу и сверху прямыми y=a, y=b. (рис. 2). Границы интегрирования a и b. Чтобы получить подынтегральное выражение, мы из уравнения правой линии вычтем уравнение левой линии. Тогда площадь трапеции:
( 6 оценок, среднее 5 из 5 )
Площадь
S
криволинейной трапеции, ограниченной
непрерывной кривой
,
двумя прямыми x=a
и x=b
и отрезком оси абсцисс
,
вычисляется по одной из следующих
формул:
,
если
на отрезке
;
,
если
на отрезке
.
Площадь
S
фигуры, ограниченной двумя непрерывными
кривыми
и
и двумя прямыми x=a
и x=b,
где
на отрезке,
вычисляется по формуле
.
Рассмотрим
примеры.
1.
Вычислить площадь, ограниченную
параболой
,
прямыми x=2,
x=4
и осью абсцисс.
Площадь
вычислим, используя формулу
.
Тогда
2.
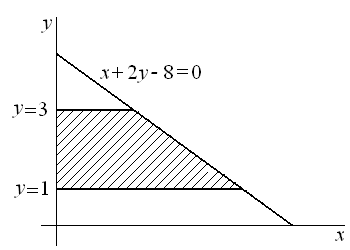
Вычислить площадь фигуры, ограниченной
прямыми
и осью ординат (рис.3).
Рис. 3
При вычислении
искомой площади учтем, что изменены
роли осей координат, т.е.:
3.
Вычислить площадь фигуры, ограниченной
ветвью гиперболы
,
прямыми x=
3,
x=
1
и осью абсцисс.
На
отрезке
функция
отрицательна. Поэтому для вычисления
площади рассматриваемой фигуры
воспользуемся формулой
.
Получим
4.
Вычислить площадь между линиями
.
Рис.4
Искомая площадь
изображена на рис. 4 и представляет
собой разность между площадью
прямоугольного треугольника OMx0
и площадью криволинейного треугольника,
ограниченного сверху участком параболы:

Абсциссу
x0
точки пересечения графиков находим,
решая совместно уравнения
,
откуда
.
Подставляя
полученное значение верхнего предела
интегрирования, получаем
-
Вычислить
площадь, ограниченную гиперболой,
осью абсцисс и ординатами
.
-
Вычислить
площадь фигуры, заключенной между
линиями
.
Изобразить фигуру графически. -
Найти
площадь фигуры, заключенной между
осью абсцисс и кривой
.
-
Найти
площадь фигуры, ограниченной кривой
,
прямыми
и осью абсцисс. -
Вычислить
площадь фигуры, образованной линиями
.
-
Определить
площадь фигуры, ограниченной параболой
и прямой
.
-
Найти
площадь фигуры, заключенной между
прямыми
и
осью абсцисс. -
Вычислить
площадь между линиями
и
.
-
Определить
площадь, ограниченную экспонентой
,
осью абсцисс и ординатами
.
-
Найти
площадь фигуры, ограниченной параболой
,
осью абсцисс и прямыми
.
§3. Приложение определенного интеграла к решению физических задач
Рассмотрим решение
следующих задач.
1.
Через участок тела животного проходит
импульс тока, который изменяется со
временем по закону
мА. Длительность импульса 0,1 с. Определить
работу, совершаемую током за это время,
если сопротивление участка равно 20
кОм.
За
малый интервал времени dt,
когда ток практически не меняется, на
сопротивлении R
совершается работа
.
За время всего импульса будет совершена
работа
.
Подставляя в
полученное выражение значение тока,
получим.
2.
Скорость точки равна
(м/с). Найти путь S,
пройденный точкой за время t=4с,
прошедшее от начала движения.
Найдем
путь
,
пройденный точкой за бесконечно малый
промежуток времени
.
Так как в течение этого времени скорость
можно считать постоянной, то
.
Интегрируя, имеем
3.
Найти силу давления жидкости на
вертикальную треугольную пластину с
основанием a
и высотой h,
погруженную в жидкость так, что ее
вершина лежит на поверхности.
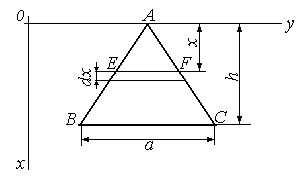
Систему координат
расположим, как показано на рис. 5.
Рис.
5
Рассмотрим
горизонтальную бесконечно малую полоску
толщиной dx,
находящуюся на произвольной глубине
x.
Принимая эту полоску за прямоугольник,
найдем ее основание EF.
Из подобия треугольников ABC
и AEF
получаем
.
Отсюда
.
Тогда площадь
полоски равна
.
Так
как сила P
давления жидкости на площадку S,
глубина погружения которой r,
по закону Паскаля равна
,
где
-
плотность жидкости, g–
ускорение силы тяжести, то искомая сила
давления на рассматриваемую площадку
dS
вычисляется по формуле
.
Следовательно,
сила давления P
жидкости на площадку ABC
.
Решить
задачи.
-
Скорость
движения точки определяется уравнением
см/с. Найти путь, пройденный точкой за
время t=5с,
протекшее от начала движения. -
Скорость
тела выражается формулой
м/с. Найти путь, пройденный телом за
первые три секунды после начала
движения. -
Скорость
движения тела определяется уравнением
см/с. Какой путь пройдет тело за третью
секунду движения? -
Два
тела начинают двигаться одновременно
из одной и той же точки: одно со скоростью
(м/мин), а другое со скоростью
(м/мин). На каком расстоянии друг от
друга они будут через 10 мин, если
двигаются по одной линии в одном
направлении? -
На
тело массой 5 г, движущееся прямолинейно,
действует сила
(дин).
Найти расстояние, пройденное телом в
течение третьей секунды движения. -
Скорость
колеблющейся точки изменяется по
закону
(см/с). Определить смещение точки через
0,1 с после начала движения. -
Какую работу
нужно совершить, чтобы растянуть
пружину на 0,06 м, если сила в 1Н растягивает
ее на 0,01 м? -
Скорость
колеблющейся точки изменяется по
закону
(м/с). Определить путь, пройденный точкой
за
с
от начала движения. -
Азот,
масса которого 7 г, расширяется при
неизменной температуре, равной 300К
так, что его объем увеличивается вдвое.
Определить работу, совершаемую газом.
Универсальная газовая постоянная
Дж/кмоль.
-
Какую
работу надо совершить, чтобы растянуть
пружину длиной в 25 см до длины в 35 см,
если известно, что коэффициент жесткости
пружины равен 400 Н/м? -
Через
тело животного проходит импульс тока,
который изменяется со временем по
закону
(мА). Длительность импульса равна 0,1с.
Определить заряд, протекающий через
тело животного. -
Какая
работа совершается при растяжении
мышцы на l
мм, если известно, что при нагрузке P0
мышца растягивается на l0
мм? Считать, что сила, необходимая для
растяжения мышц, пропорциональна ее
удлинению. -
Тело
двигается в некоторой среде прямолинейно
по закону
.
Сопротивление среды пропорционально
квадрату скорости
.
Найти работу, произведенную силой
сопротивления среды при передвижении
тела от S=0
до S=a
метров.
Соседние файлы в предмете Физика
- #
- #
- #
Вычисление площадей плоских фигур является одним из приложений определенного интеграла.
Для того, чтобы получить площадь фигуры изображенной на рисунке, необходимо
вычислить определенный интеграл
вида:
Функции
и
как правило, известны из условия задачи, а вот абсциссы их точек пересечения
и
придется дополнительно найти. Для этого необходимо решить уравнение:
Описанным выше способом, можно также найти площадь криволинейной трапеции в случае, если графики функций
и
не пересекаются, но точки
и
заданы по условию задачи:
В этом случае криволинейная трапеция (фигура площадь которой мы вычисляем) образована графиками функций
,
и прямыми
,
.
Онлайн калькулятор, построенный на основе системы Wolfram Alpha, автоматически вычислит площадь фигуры, образованной пересечением двух графиков функций.