Как найти площадь геометрической прогрессии

Как найти площадь геометрической прогрессии

Перед нами бесконечно убывающая геометрическая прогрессия.

Площади квадратов S1,S2,S3,… являются членами этой бесконечно убывающей геометрической прогрессии, первый член которой – площадь самого большого квадрата S1 – равен единице, а знаменатель (q) равен 1/2.

Известно, что для такой прогрессии можно вычислить сумму ее членов, как число к которому неограниченно приближается сумма первых членов рассматриваемой прогрессии при неограниченном возрастании числа n, где n – порядковый номер членов прогрессии.

Как вычисляется:

Найдем значения нескольких первых членов прогрессии.

1) Площадь самого большого квадрата со стороной b1 = 1 см:

S1 = 1*1 = 1

2) Для нахождения S2 сначала вычислим по теореме Пифагора длину стороны второго квадрата:

1/2)*(1/2) + (1/2)*(1/2) = 2/4 = 1/2, извлекаем корень, получаем b2 = 1/(корень из двух). Некоторые действия приходится писать словами, увы.

Находим площадь второго квадрата, она равна S2 = 1/2

3) Аналогично, площадь третьего квадрата будет равна S3 = 1/4, ну и т.д.

Чтобы найти знаменатель геометрической прогрессии, нужно поделить значение последующего члена прогрессии на предыдущий, например: S2 поделить на S1. В результате получаем, что знаменатель нашей прогрессии равен q = 1/2.

Теперь находим сумму всех площадей квадратов по известной формуле суммы членов бесконечно убывающей геометрической прогрессии:

S = S1/(1-q)

S = 1/(1 – 1/2) = 2

Ответ: искомая площадь равна 2.

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 декабря 2022 года; проверки требуют 37 правок.

У этого термина существуют и другие значения, см. Прогрессия.

Геометри́ческая прогре́ссия — последовательность чисел b_{1}, b_{2}, b_{3}, ldots (члены прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего члена умножением его на фиксированное число q (знаменатель прогрессии). При этом {displaystyle b_{1}neq 0,qneq 0;b_{n}=b_{n-1}q,nin mathbb {N} ,ngeqslant 2}[1].

Геометрическая прогрессия называется бесконечно убывающей[2], если знаменатель прогрессии по абсолютной величине меньше единицы.

Произведением первых n членов геометрической прогрессии {displaystyle left{b_{n}right}} называется произведение от b_{1} до b_n, то есть выражение вида {displaystyle prod limits _{i=1}^{n}b_{i}=b_{1}cdot b_{2}cdot b_{3}cdot ldots cdot b_{n-2}cdot b_{n-1}cdot b_{n}.}
Обозначение: P_{n}.

Описание[править | править код]

Любой член геометрической прогрессии может быть вычислен по формуле

{displaystyle b_{n}=b_{1}q^{n-1}.}

Если {displaystyle b_{1}>0} и {displaystyle q>1}, прогрессия является возрастающей последовательностью, если {displaystyle 0<q<1}, — убывающей последовательностью, а при q<0 — знакочередующейся[3], при q=1 — стационарной (постоянной).

Своё название прогрессия получила по своему характеристическому свойству:

{displaystyle |b_{n}|={sqrt {b_{n-1}b_{n+1}}},}

то есть модуль любого члена геометрической прогрессии, кроме первого, равен среднему геометрическому (среднему пропорциональному) двух рядом с ним стоящих членов[4].

Примеры[править | править код]

Получение новых квадратов путём соединения середин сторон предыдущих квадратов

  • Последовательность площадей квадратов, где каждый следующий квадрат получается соединением середин сторон предыдущего — бесконечная геометрическая прогрессия со знаменателем 1/2. Площади получающихся на каждом шаге треугольников также образуют бесконечную геометрическую прогрессию со знаменателем 1/2, сумма которой равна площади начального квадрата[5]:8—9.
  • Геометрической является последовательность количества зёрен на клетках в задаче о зёрнах на шахматной доске.
  • 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192 — геометрическая прогрессия со знаменателем 2 из тринадцати членов.
  • 50; 25; 12,5; 6,25; 3,125; … — бесконечно убывающая геометрическая прогрессия со знаменателем 1/2.
  • 4; 6; 9 — геометрическая прогрессия из трёх элементов со знаменателем 3/2.
  • pi , pi , pi , pi  — стационарная геометрическая прогрессия со знаменателем 1 (и стационарная арифметическая прогрессия с разностью 0).
  • 3; −6; 12; −24; 48; … — знакочередующаяся геометрическая прогрессия со знаменателем −2.
  • 1; −1; 1; −1; 1; … — знакочередующаяся геометрическая прогрессия со знаменателем −1.

Свойства[править | править код]

Свойства знаменателя геометрической прогрессии[править | править код]

Знаменатель геометрической прогрессии можно найти по формулам:

  • {displaystyle q={dfrac {b_{n+1}}{b_{n}}}}

Доказательство

По определению геометрической прогрессии.

  • {displaystyle q={sqrt[{n-k}]{dfrac {b_{n}}{b_{k}}}},{text{где }}k<n;;forall n,forall kin mathbb {N} .}

Свойства членов геометрической прогрессии[править | править код]

  • Рекуррентное соотношение для геометрической прогрессии:
{displaystyle b_{n}=b_{n-1}cdot q}

Доказательство

По определению геометрической прогрессии.

  • Формула общего (n-го) члена:
{displaystyle b_{n}=b_{1}cdot q^{n-1}.}
  • Обобщённая формула общего члена:
{displaystyle b_{n}=b_{k}cdot q^{n-k},{text{где }}k<n;;forall n,forall kin mathbb {N} .}

Доказательство

{displaystyle b_{n}^{2}=b_{n}b_{n}=b_{1}q^{n-1}b_{1}q^{n-1}=b_{1}q^{n-1-i}b_{1}q^{n-1+i}=b_{n-i}b_{n+i}.}

  • Логарифмы членов геометрической прогрессии (если определены) образуют арифметическую прогрессию.

Доказательство

{displaystyle log(b_{n})=log(b_{1}q^{n-1})=log(b_{1})+(n-1)cdot log(q)}
Формула общего члена арифметической прогрессии:
{displaystyle a_{n}=a_{1}+(n-1)cdot d}.
В нашем случае
a_{1}=log(b_{1}),
d=log(q).

Доказательство

{displaystyle b_{n}^{2}=b_{n}b_{n}=b_{1}q^{n-1}b_{1}q^{n-1}=b_{1}q^{n-1-i}b_{1}q^{n-1+i}=b_{n-i}b_{n+i}.}

Пусть {displaystyle a_{k},a_{l},a_{m}} — соответственно k-й, l-й, m-й члены геометрической прогрессии, где {displaystyle k,,l,,min mathbb {N} }. Тогда для всякой такой тройки выполняется комплементарное свойство геометрической прогрессии, называемое тождеством геометрической прогрессии:

{displaystyle b_{k}^{l-m}cdot b_{l}^{m-k}cdot b_{m}^{k-l}=1.}

  • Произведение членов геометрической прогрессии начиная с k-го члена, и заканчивая n-м членом, можно рассчитать по формуле
    {displaystyle P_{k,n}={dfrac {P_{n}}{P_{k-1}}}.}

Доказательство

{displaystyle P_{k,n}=prod _{i=k}^{n}b_{i}={frac {prod _{i=1}^{n}b_{i}}{prod _{j=1}^{k-1}b_{j}}}={frac {P_{n}}{P_{k-1}}}.}

  • Сумма всех членов убывающей прогрессии:
{displaystyle left|qright|<1}, то {displaystyle b_{n}to 0} при nto +infty , и
{displaystyle S_{n}to {frac {b_{1}}{1-q}}} при nto +infty .

Свойства суммы геометрической прогрессии[править | править код]

  • {displaystyle b_{n+1}=S_{n+1}-S_{n}}
  • {displaystyle S_{n}=sigma _{n}cdot b_{1}b_{n}}

где {displaystyle sigma _{n}} — сумма обратных величин, т. е. {displaystyle sigma _{n}={dfrac {1}{b_{1}}}+{dfrac {1}{b_{2}}}+cdots +{dfrac {1}{b_{n-1}}}+{dfrac {1}{b_{n}}}}.

Свойства произведения геометрической прогрессии[править | править код]

См. также[править | править код]

  • Арифметическая прогрессия
  • Арифметико-геометрическая прогрессия
  • Числа Фибоначчи
  • Показательная функция
  • Сумма ряда

Примечания[править | править код]

  1. ↑ Геометрическая прогрессия Архивная копия от 12 октября 2011 на Wayback Machine на mathematics.ru
  2. ↑ Это название, хотя и является общепринятым, неудачно, так как бесконечно убывающая геометрическая прогрессия является убывающей, только если и первый член, и знаменатель прогрессии положительны.
  3. ↑ Геометрическая прогрессия // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
  4. ↑ Если геометрическая прогрессия является конечной последовательностью, то её последний член таким свойством не обладает.
  5. ↑ Роу С. Геометрические упражнения с куском бумаги. — 2-е изд. — Одесса: Mathesis, 1923. Архивная копия от 19 мая 2017 на Wayback Machine
Источник

Определение геометрической прогрессии:

Рассмотрим последовательность, членами которой являются степени числа 2 с натуральными показателями:

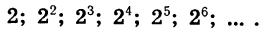
Геометрическая прогрессия

Каждый член этой последовательности, начиная со второго, получается умножением предыдущего члена на 2. Эта последовательность является примером геометрической прогрессии.

Определение:

Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число.

Иначе говоря, последовательность 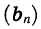Геометрическая прогрессия — геометрическая прогрессия, если для любого натурального п выполняются условия

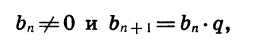
Геометрическая прогрессия

где q — некоторое число. Обозначим, например, через 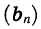Геометрическая прогрессияпоследовательность натуральных степеней числа 2. В этом случае для любого натурального п верно равенство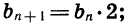Геометрическая прогрессия здесь q = 2.

Из определения геометрической прогрессии следует, что отношение любого ее члена, начиная со второго, к предыдущему члену равно q, т. е. при любом натуральном n верно равенство

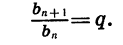
Геометрическая прогрессия


Число q называют знаменателем геометрической прогрессии.

Очевидно, что знаменатель геометрической прогрессии отличен от нуля.

Чтобы задать геометрическую прогрессию, достаточно указать ее первый член и знаменатель.

Приведем примеры.

Если 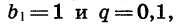Геометрическая прогрессиято получим геометрическую прогрессию

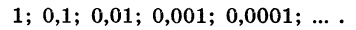
Геометрическая прогрессия

Условиями 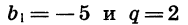Геометрическая прогрессиязадается геометрическая прогрессия

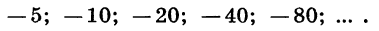
Геометрическая прогрессия

Если 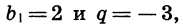Геометрическая прогрессия то имеем прогрессию

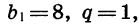Геометрическая прогрессия

Если Геометрическая прогрессия то получим геометрическую прогрессию

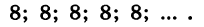
Геометрическая прогрессия

Зная первый член и знаменатель геометрической прогрессии, можно найти последовательно второй, третий и вообще любой ее член:

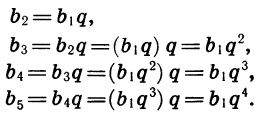
Геометрическая прогрессия

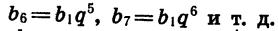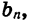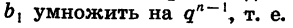
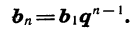
Точно так же находим, что Геометрическая прогрессия Вообще, чтобы найти Геометрическая прогрессия мы должны Геометрическая прогрессия

Геометрическая прогрессия

Мы получили формулу n-го члена геометрической прогрессии.

Приведем примеры решения задач с использованием этой формулы.

Пример:

В геометрической прогрессии 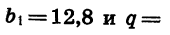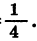Геометрическая прогрессияГеометрическая прогрессияНайдем b7.

По формуле n-го члена геометрической прогрессии

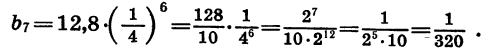
Геометрическая прогрессия

Пример:

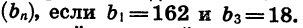
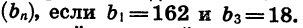
Найдем восьмой член геометрической прогрессииГеометрическая прогрессия

Геометрическая прогрессия

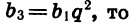
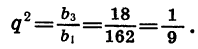
Зная первый и третий члены геометрической прогрессии, можно найти ее знаменатель. Так как Геометрическая прогрессия

Геометрическая прогрессия

Решив уравнение

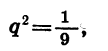
Геометрическая прогрессия

найдем, что

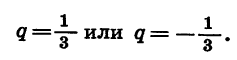
Геометрическая прогрессия

Таким образом, существуют две прогрессии, удовлетворяющие условию задачи.

Если

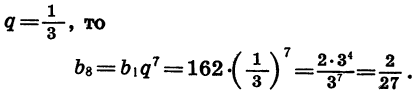
Геометрическая прогрессия

Если

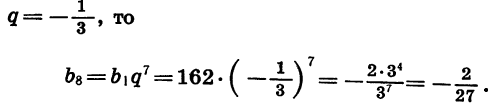
Геометрическая прогрессия

Задача имеет два решения:

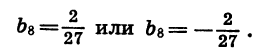
Геометрическая прогрессия

Пример:

После каждого движения поршня разрежающего насоса из сосуда удаляется 20% находящегося в нем воздуха. Определим давление воздуха внутри сосуда, после шести движений поршня, если первоначально давление было 760 мм рт. ст.

Так как после каждого движения поршня из сосуда удаляется 20% имевшегося воздуха, то остается 80% воздуха. Чтобы узнать давление воздуха в сосуде после очередного движения поршня, нужно давление после предыдущего движения поршня умножить на 0,8.

Мы имеем геометрическую прогрессию, первый член которой равен 760, а знаменатель равен 0,8. Число, выражающее давление воздуха в сосуде (в мм рт. ст.) после шести движений поршня, является седьмым членом этой прогрессии. Оно равно

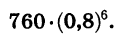
Геометрическая прогрессия

Произведя вычисления, получим:

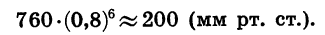
Геометрическая прогрессия

Формула суммы n первых членов геометрической прогрессии

Древняя индийская легенда рассказывает, что изобретатель шахмат попросил в награду за свое изобретение столько пшеничных зерен, сколько их получится, если на первую клетку шахматной доски положить одно зерно, на вторую — в 2 раза больше, т. е. 2 зерна, на третью — еще в 2 раза больше, т. е. 4 зерна, и т. д. до 64-й клетки. Сколько зерен должен был получить изобретатель шахмат?

Число зерен, о которых идет речь, является суммой шестидесяти четырех членов геометрической прогрессии, первый член которой равен 1, а знаменатель равен 2. Обозначим эту сумму через S:

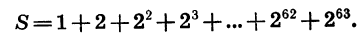
Геометрическая прогрессия

Умножим обе части записанного равенства на знаменатель прогрессии, получим:

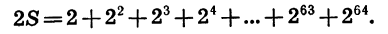
Геометрическая прогрессия

Вычтем почленно из второго равенства первое и проведем упрощения:

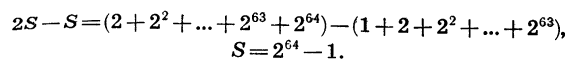
Геометрическая прогрессия

Можно подсчитать, что масса такого числа пшеничных зерен больше триллиона тонн. Это заведомо превосходит количество пшеницы, собранной человечеством до настоящего времени.

Выведем теперь формулу суммы n первых членов произвольной геометрической прогрессии. Воспользуемся тем же приемом, с помощью которого была вычислена сумма S.

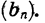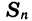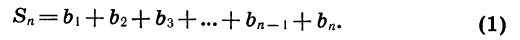
Пусть дана геометрическая прогрессия Геометрическая прогрессияОбозначим сумму n первых ее членов через Геометрическая прогрессия:

Геометрическая прогрессия

Умножим обе части этого равенства на q:

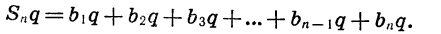
Геометрическая прогрессия

Учитывая, что

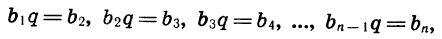
Геометрическая прогрессия

получим:

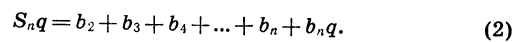
Геометрическая прогрессия

Вычтем почленно из равенства (2) равенство (1) и приведем подобные члены:

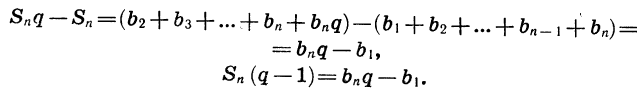
Геометрическая прогрессия

Отсюда следует, что при 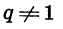Геометрическая прогрессия

Геометрическая прогрессия

Мы получили формулу суммы n первых членов геометрической прогрессии, в которой 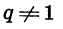Геометрическая прогрессия. Если q = 1, то все члены прогрессии равны первому члену и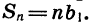 Геометрическая прогрессия

При решении многих задач удобно пользоваться формулой суммы п первых членов геометрической прогрессии, записанной в другом виде. Подставим в формулу (I) вместо 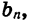Геометрическая прогрессия выражение 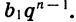Геометрическая прогрессия Получим:

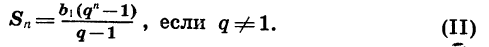
Геометрическая прогрессия

Пример:

Найдем сумму первых десяти членов геометрической прогрессии 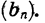Геометрическая прогрессия в которой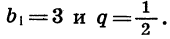 Геометрическая прогрессия

Так как известны первый член и знаменатель прогрессии, то удобно воспользоваться формулой (II). Получим:

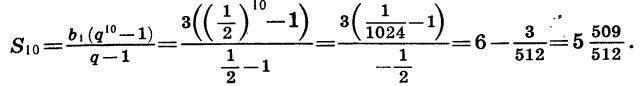
Геометрическая прогрессия

Пример:

Найдем сумму 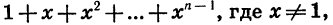Геометрическая прогрессия слагаемые которой являются последовательными членами геометрической прогрессии

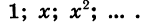
Геометрическая прогрессия

Первый член прогрессии равен 1, а знаменатель равен х. Так как 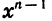Геометрическая прогрессия является членом этой прогрессии с номером n, то задача состоит в нахождении суммы п первых ее членов. Воспользуемся формулой (I):

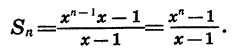
Геометрическая прогрессия

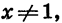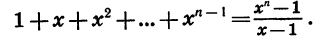
Таким образом, если Геометрическая прогрессия то

Геометрическая прогрессия

Умножив левую и правую части последнего равенства на х — 1, получим тождество

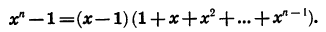
Геометрическая прогрессия

В частности, при n = 2 и n = 3 приходим к известным формулам

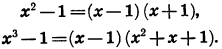
Геометрическая прогрессия

Пример:

Найдем сумму шести первых членов геометрической прогрессии 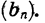Геометрическая прогрессия если известно, что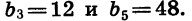 Геометрическая прогрессия

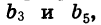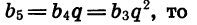
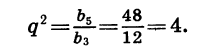
Зная Геометрическая прогрессияможно найти знаменатель прогрессии q. Так как Геометрическая прогрессия

Геометрическая прогрессия

Значит,

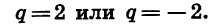
Геометрическая прогрессия

Таким образом, существуют две прогрессии, удовлетворяющие условию задачи.

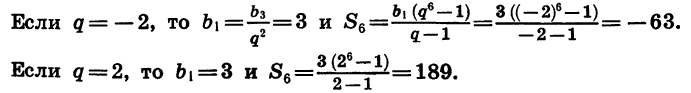
Геометрическая прогрессия

Сумма бесконечной геометрической прогрессии при |q|< 1

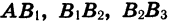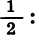
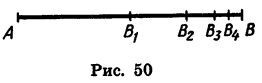
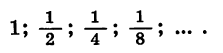
Пусть длина отрезка АВ равна 2 ед. (рис. 50). Отметим точку В1 — середину отрезка А В, затем точку В2 — середину правой его половины, затем точку В3 — середину получившегося справа отрезка и т. д. Длины отрезков Геометрическая прогрессияи т. д. образуют бесконечную геометрическую прогрессию, знаменатель которой равен Геометрическая прогрессия

Геометрическая прогрессия

Геометрическая прогрессия

Найдем сумму n первых членов этой прогрессии:

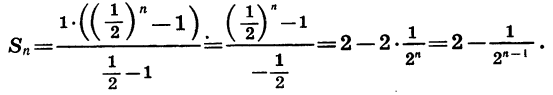
Геометрическая прогрессия

При увеличении числа слагаемых n значение дроби 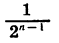Геометрическая прогрессия приближается к нулю. Действительно,

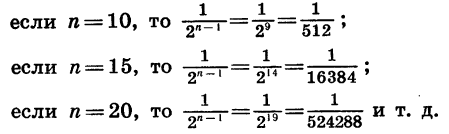
Геометрическая прогрессия

Поэтому при неограниченном увеличении n разность 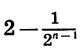Геометрическая прогрессиястановится сколь угодно близкой к числу 2 или, как говорят, стремится к числу 2.

Таким образом, сумма n первых членов геометрической прогрессии 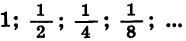Геометрическая прогрессия при неограниченном увеличении n стремится к числу 2. Число 2 называют суммой бесконечной геометрической прогрессии 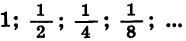Геометрическая прогрессия и пишут:

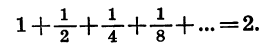
Геометрическая прогрессия

Это равенство легко истолковать геометрически: сумма длин отрезков 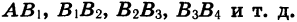Геометрическая прогрессия равна длине отрезка АВ.

Рассмотрим теперь произвольную геометрическую прогрессию

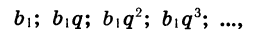
Геометрическая прогрессия

у которой |q|< 1

Запишем формулу суммы п первых членов прогрессии:

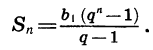
Геометрическая прогрессия

Преобразуем выражение в правой части равенства:

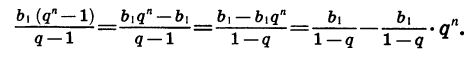
Геометрическая прогрессия

Значит,

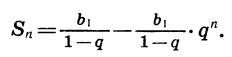
Геометрическая прогрессия

Можно доказать, что если 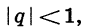Геометрическая прогрессия то при неограниченном увеличении n множитель 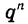Геометрическая прогрессия стремится к нулю, а значит, стремится к нулю и произведение 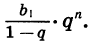Геометрическая прогрессия Поэтому при неограниченном увеличении n сумма Sn стремится к числу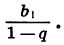 Геометрическая прогрессия

Число 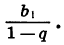Геометрическая прогрессия называют суммой бесконечной геометрической прогрессии 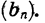Геометрическая прогрессия у которой Геометрическая прогрессия

Это записывают так:

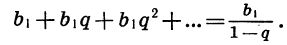
Геометрическая прогрессия

Обозначив сумму прогрессии 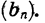Геометрическая прогрессиябуквой S, получим формулу

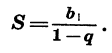
Геометрическая прогрессия

Заметим, что если 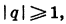Геометрическая прогрессия то сумма n первых членов геометрической прогрессии при неограниченном увеличении n не стремится ни к какому числу. Бесконечная геометрическая прогрессия имеет сумму только при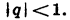 Геометрическая прогрессия

Пример:

Найдем сумму бесконечной геометрической прогрессии 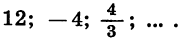Геометрическая прогрессия

У этой прогрессии 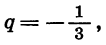Геометрическая прогрессия значит, условие |q| < 1 выполнено. По формуле 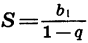Геометрическая прогрессия получим:

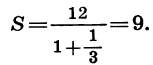
Геометрическая прогрессия

Пример:

Дан квадрат, сторона которого равна 4 см. Середины его сторон являются вершинами второго квадрата, середины сторон второго квадрата являются вершинами третьего квадрата и т. д. (рис. 51). Найдем сумму площадей всех квадратов.

Из геометрических соображений ясно, что площадь каждого следующего квадрата равна половине площади предыдущего. Таким образом, последовательность площадей квадратов является геометрической прогрессией, первый член которой равен 16, а знаменатель равен 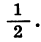Геометрическая прогрессия Найдем сумму этой геометрической прогрессии:

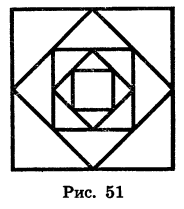
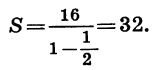
Геометрическая прогрессия

Геометрическая прогрессия

Значит, сумма площадей всех квадратов равна 32 см2.

Из курса VIII класса нам известно, что каждое рациональное число может быть представлено в виде бесконечной десятичной периодической дроби. Чтобы выразить рациональное число 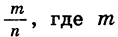Геометрическая прогрессия — целое число, а n — натуральное, в виде бесконечной десятичной дроби, достаточно разделить числитель на знаменатель. Наоборот, каждая бесконечная десятичная периодическая дробь представляет некоторое рациональное число. Покажем на примере, как с помощью формулы суммы бесконечной геометрической прогрессии можно представить бесконечную десятичную периодическую дробь в виде отношения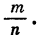 Геометрическая прогрессия

Пример:

Представим бесконечную десятичную периодическую дробь 0,(18) в виде обыкновенной дроби.

По аналогии с конечными десятичными дробями представим бесконечную десятичную дробь 0,(18) в виде суммы:

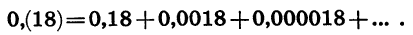
Геометрическая прогрессия

Слагаемые в правой части равенства — члены геометрической прогрессии, у которой первый член равен 0,18, а знаменатель равен 0,01, т. е. условие 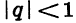Геометрическая прогрессия выполнено. Найдем сумму этой прогрессии:

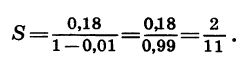
Геометрическая прогрессия

Значит,

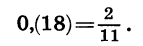
Геометрическая прогрессия

Таким же способом можно представить в виде обыкновенной дроби любую бесконечную десятичную периодическую дробь.

Решение заданий и задач по предметам:

  • Математика
  • Высшая математика
  • Математический анализ
  • Линейная алгебра

Дополнительные лекции по высшей математике:

  1. Тождественные преобразования алгебраических выражений
  2. Функции и графики
  3. Преобразования графиков функций
  4. Квадратная функция и её графики
  5. Алгебраические неравенства
  6. Неравенства
  7. Неравенства с переменными
  8. Прогрессии в математике
  9. Арифметическая прогрессия
  10. Показатели в математике
  11. Логарифмы в математике
  12. Исследование уравнений
  13. Уравнения высших степеней
  14. Уравнения высших степеней с одним неизвестным
  15. Комплексные числа
  16. Непрерывная дробь (цепная дробь)
  17. Алгебраические уравнения
  18. Неопределенные уравнения
  19. Соединения
  20. Бином Ньютона
  21. Число е
  22. Непрерывные дроби
  23. Функция
  24. Исследование функций
  25. Предел
  26. Интеграл
  27. Двойной интеграл
  28. Тройной интеграл
  29. Интегрирование
  30. Неопределённый интеграл
  31. Определенный интеграл
  32. Криволинейные интегралы
  33. Поверхностные интегралы
  34. Несобственные интегралы
  35. Кратные интегралы
  36. Интегралы, зависящие от параметра
  37. Квадратный трехчлен
  38. Производная
  39. Применение производной к исследованию функций
  40. Приложения производной
  41. Дифференциал функции
  42. Дифференцирование в математике
  43. Формулы и правила дифференцирования
  44. Дифференциальное исчисление
  45. Дифференциальные уравнения
  46. Дифференциальные уравнения первого порядка
  47. Дифференциальные уравнения высших порядков
  48. Дифференциальные уравнения в частных производных
  49. Тригонометрические функции
  50. Тригонометрические уравнения и неравенства
  51. Показательная функция
  52. Показательные уравнения
  53. Обобщенная степень
  54. Взаимно обратные функции
  55. Логарифмическая функция
  56. Уравнения и неравенства
  57. Положительные и отрицательные числа
  58. Алгебраические выражения
  59. Иррациональные алгебраические выражения
  60. Преобразование алгебраических выражений
  61. Преобразование дробных алгебраических выражений
  62. Разложение многочленов на множители
  63. Многочлены от одного переменного
  64. Алгебраические дроби
  65. Пропорции
  66. Уравнения
  67. Системы уравнений
  68. Системы уравнений высших степеней
  69. Системы алгебраических уравнений
  70. Системы линейных уравнений
  71. Системы дифференциальных уравнений
  72. Арифметический квадратный корень
  73. Квадратные и кубические корни
  74. Извлечение квадратного корня
  75. Рациональные числа
  76. Иррациональные числа
  77. Арифметический корень
  78. Квадратные уравнения
  79. Иррациональные уравнения
  80. Последовательность
  81. Ряды сходящиеся и расходящиеся
  82. Тригонометрические функции произвольного угла
  83. Тригонометрические формулы
  84. Обратные тригонометрические функции
  85. Теорема Безу
  86. Математическая индукция
  87. Показатель степени
  88. Показательные функции и логарифмы
  89. Множество
  90. Множество действительных чисел
  91. Числовые множества
  92. Преобразование рациональных выражений
  93. Преобразование иррациональных выражений
  94. Геометрия
  95. Действительные числа
  96. Степени и корни
  97. Степень с рациональным показателем
  98. Тригонометрические функции угла
  99. Тригонометрические функции числового аргумента
  100. Тригонометрические выражения и их преобразования
  101. Преобразование тригонометрических выражений
  102. Комбинаторика
  103. Вычислительная математика
  104. Прямая линия на плоскости и ее уравнения
  105. Прямая и плоскость
  106. Линии и уравнения
  107. Прямая линия
  108. Уравнения прямой и плоскости в пространстве
  109. Кривые второго порядка
  110. Кривые и поверхности второго порядка
  111. Числовые ряды
  112. Степенные ряды
  113. Ряды Фурье
  114. Преобразование Фурье
  115. Функциональные ряды
  116. Функции многих переменных
  117. Метод координат
  118. Гармонический анализ
  119. Вещественные числа
  120. Предел последовательности
  121. Аналитическая геометрия
  122. Аналитическая геометрия на плоскости
  123. Аналитическая геометрия в пространстве
  124. Функции одной переменной
  125. Высшая алгебра
  126. Векторная алгебра
  127. Векторный анализ
  128. Векторы
  129. Скалярное произведение векторов
  130. Векторное произведение векторов
  131. Смешанное произведение векторов
  132. Операции над векторами
  133. Непрерывность функций
  134. Предел и непрерывность функций нескольких переменных
  135. Предел и непрерывность функции одной переменной
  136. Производные и дифференциалы функции одной переменной
  137. Частные производные и дифференцируемость функций нескольких переменных
  138. Дифференциальное исчисление функции одной переменной
  139. Матрицы
  140. Линейные и евклидовы пространства
  141. Линейные отображения
  142. Дифференциальные теоремы о среднем
  143. Теория устойчивости дифференциальных уравнений
  144. Функции комплексного переменного
  145. Преобразование Лапласа
  146. Теории поля
  147. Операционное исчисление
  148. Системы координат
  149. Рациональная функция
  150. Интегральное исчисление
  151. Интегральное исчисление функций одной переменной
  152. Дифференциальное исчисление функций нескольких переменных
  153. Отношение в математике
  154. Математическая логика
  155. Графы в математике
  156. Линейные пространства
  157. Первообразная и неопределенный интеграл
  158. Линейная функция
  159. Выпуклые множества точек
  160. Система координат

Источник

Содержание

Геометрическая прогрессия

q – знаменатель геометрической прогрессии (от лат. qwoti — частное).
$$
b_n = b_{n-1} cdot q\[10pt]
b_n = b_{1} cdot q^{n-1}
$$

Если $ b_{1}>0$ и $ q>1$, прогрессия является возрастающей последовательностью, если $ 0<q<1$, — убывающей последовательностью, а при $q<0$  — знакочередующейся.

Пример 1.

Пример 2.
Последовательность площадей квадратов, где каждый следующий квадрат получается соединением середин сторон предыдущего — бесконечная геометрическая прогрессия со знаменателем 1/2.

Пример 3.

The Quadrature of the Parabola – Wikipedia

Пример 4. Фракталы – Кривая Коха (снежинка Коха)

Берём единичный отрезок, разделяем на три равные части и заменяем средний интервал равносторонним треугольником без этого сегмента. В результате образуется ломаная, состоящая из четырёх звеньев длины 1/3. На следующем шаге повторяем операцию для каждого из четырёх получившихся звеньев и т. д… Предельная кривая и есть кривая Коха.

Непрерывна, но нигде не дифференцируема.

Koch snowflake – Wikipedia

Площадь снежинки Коха составляет 8/5 площади оригинального треугольника.

Площадь внутри снежинки Коха можно описать как объединение бесконечного числа равносторонних треугольников (см. рисунок).
Каждая сторона зеленого треугольника = 1/3 длины стороны большого синего треугольника,
и поэтому площадь зеленого = 1/9 площади синего. Аналогично, каждый желтый треугольник имеет площадь = 1/9 площади зеленого треугольника, и так далее.
Возьмем синий треугольник за единицу площади, общая площадь снежинки равна

$ 1,+,3left({frac {1}{9}}right),+,12left({frac {1}{9}}right)^{2},+,48left({frac {1}{9}}right)^{3},+,cdots .$

The first term of this series represents the area of the blue triangle, the second term the total area of the three green triangles, the third term the total area of the twelve yellow triangles, and so forth. Excluding the initial 1, this series is geometric with constant ratio r = 4/9. The first term of the geometric series is a = 3(1/9) = 1/3, so the sum is

$ 1,+,{frac {a}{1-r}};=;1,+,{frac {frac {1}{3}}{1-{frac {4}{9}}}};=;{frac {8}{5}}.$

Характеристическое свойство

Характеристическое свойство: числовая последовательность ${b_n}$ является геометрической прогрессией тогда и только тогда, когда любой член этой последовательности, начиная со второго, есть среднее геометрическое соседних с ним членов.
$$
b_n^2 = b_{n-1} cdot b_{n+1} \[10pt]
|b_n| = sqrt{b_{n-1} cdot b_{n+1}}\[20pt]

b_k cdot b_l = b_m cdot b_n ; text{ если } ; k+l = m + n
$$

Свойство:
Произведение первых n членов геометрической прогрессии можно рассчитать по формуле:

$ P_{n}=(b_{1}cdot b_{n})^{frac n 2 }$

Сумма геометрической прогрессии

$$
S_n = frac {b_{1} (q^n-1)} {q-1}, quad q ne 1
$$

Сумма бесконечной геометрической прогрессии, в которой |q| < 1, равна первому члену, деленному на 1 – знаменатель прогрессии.
$$ text{при } |q|<1 : quad S = frac {b_1}{1-q}
$$

Равенство это имеет необычный характер, так как в левой его части мы не можем буквально сложить всё «бесконечное множество» слагаемых. Оно выражает лишь то, что чем больше слагаемых левой части мы сложим, тем меньше наша сумма будет отличаться от $frac {b_1}{1-q}$.

В учебнике Виленкина упоминается «Сумма бесконечно убывающей геометрической прогрессии выражается формулой…» – это неверно, так как при отрицательных q, |q|<1, получаем знакочередующуюся последовательность, которая не может быть убывающей

Первоначальная формулировка: если $|q|<1$, то при неограниченном возрастании числа $n$ сумма $S_n$ стремится к числу $frac{b_1}{1-q}$. Это число называется суммой бесконечной геометрической прогрессии при |q|<1.

Cумма геометрической прогрессии со знаменателем q, b=1 :

$$S=1 + q +q^2+cdots=1+q(1+q+cdots) = 1+qcdot S$$

Отсюда выразить S.

Эта же техника может быть использована при вычислении любых самоподобных выражений.

Формула суммы сходящейся геометрической прогрессии была известна до Эйлера.

$$ S = frac {b_{n+1}-b_1}{q-1}
$$

Периодические дроби

Обращение бесконечных периодических дробей в обыкновенные дроби:

$0,(7) = 0,7+0,07+0,007+ldots = 0,7 / (1-0.1) = 7/10 / (9/10) = 7/9$

$0.9999ldots ;=;{frac {9}{9}};=;1.$

см. также 0.999… – Wikipedia

Геометрическая интерпретация

q=1/2, S=1:

q=1/4, S=1/3:

Сходимость геометрической прогрессии при q=1/2, b=1/2:

Шутка

В магазин заходит бесконечное число математиков. Первый просит килограмм картошки, второй – полкило, третий – четверть… «Понял», – говорит продавец и кладет на прилавок два килограмма.

Легенда о шахматной доске

Шахматы – одна из самых древних игр. Она существует уже многие века, и неудивительно, что с нею связаны различные предания, правдивость которых, за давностью времени, невозможно проверить.

Об одной из подобных легенд и математической составляющей ее содержания мы сегодня и поведём речь. Чтобы понять ее, не нужно вовсе уметь играть в шахматы: достаточно знать, что игра происходит на доске, разграфленной на 64 клетки.

Шахматная игра была придумана в Индии, и когда индусский царь Шерам познакомился с нею, он был восхищен ее остроумием и разнообразием возможных в ней положений. Узнав, что она изобретена одним из его подданных, царь приказал его позвать, чтобы лично наградить за удачную выдумку.

– Я достаточно богат, чтобы исполнить самое смелое твое пожелание, – сказал царь.– Назови награду, которая тебя удовлетворит, и ты получишь ее.

он удивил царя беспримерной скромностью своей просьбы.

– Повелитель, – сказал Сета,– прикажи выдать мне за первую клетку шахматной доски одно пшеничное зерно.

– Простое пшеничное зерно? – изумился царь.

– Да, повелитель. За вторую клетку прикажи выдать 2 зерна, за третью 4, за четвертую – 8, за пятую – 16, за шестую – 32…

–Довольно, – с раздражением прервал его царь.– Ты получишь свои зерна за все 64 клетки доски, согласно твоему желанию: за каждую вдвое больше против предыдущей. Но знай, что просьба твоя недостойна моей щедрости. Прося такую ничтожную награду, ты непочтительно пренебрегаешь моею милостью. Поистине, как учитель, ты мог бы показать лучший пример уважения к доброте своего государя. Ступай. Слуги мои вынесут тебе твой мешок с пшеницей.

За обедом царь вспомнил об изобретателе шахмат и послал узнать, унес ли уже безрассудный Сета свою жалкую награду.

– Повелитель, – был ответ, – приказание твое исполняется. Придворные математики исчисляют число следуемых зерен.

Царь нахмурился. Он не привык, чтобы повеления его исполнялись так медлительно.

Вечером, отходя ко сну, царь еще раз осведомился, давно ли Сета со своим мешком пшеницы покинул ограду дворца.

– Повелитель, – ответили ему,– математики твои трудятся без устали и надеются еще до рассвета закончить подсчет.

– Почему медлят с этим делом? – гневно воскликнул царь. – Завтра, прежде чем я проснусь, все до последнего зерна должно быть выдано Сете. Я дважды не приказываю.

Утром царю доложили, что старшина придворных математиков просит выслушать важное донесение. Царь приказал ввести его.

– Прежде чем скажешь о твоем деле, – объявил Шерам,– я желаю услышать, выдана ли, наконец, Сете та ничтожная награда, которую он себе назначил.

– Ради этого я и осмелился явиться перед тобой в столь ранний час,– ответил старик.– Мы добросовестно исчислили все количество зерен, которое желает получить Сета. Число это так велико…

– Как бы велико оно ни было, – надменно перебил царь, житницы мои не оскудеют. Награда обещана и должна быть выдана…

– Не в твоей власти, повелитель, исполнять подобные желания. Во всех амбарах твоих нет такого числа зерен, какое потребовал Сета. Нет его и в житницах целого царства. Не найдется такого числа зерен и на всем пространстве Земли. И если желаешь непременно выдать обещанную награду, то прикажи превратить земные царства в пахотные поля, прикажи осушить моря и океаны, прикажи растопить льды и снега, покрывающие далекие северные пустыни. Пусть все пространство их сплошь будет засеяно пшеницей. И все то, что родится на этих полях, прикажи отдать Сете. Тогда он получит свою награду. С изумлением внимал царь словам старца.

– Назови же мне это чудовищное число, – сказал он в раздумье.

– Восемнадцать квинтиллионов четыреста сорок шесть квадриллионов семьсот сорок четыре триллиона семьдесят три биллиона семьсот девять миллионов пятьсот пятьдесят одна тысяча шестьсот пятнадцать, о повелитель!

S = 18 446 744 073 709 551 615.

Это количество зерна примерно в 1800 раз превышает мировой урожай пшеницы за год (в 2008 – 2009 аграрном году урожай составил 686 млн тонн), то есть превышает весь урожай пшеницы, собранный за всю историю человечества.

Индусский царь не в состоянии был выдать подобной награды. Но он легко мог бы, будь он силен в математике, освободиться от столь обременительного долга. Для этого нужно было лишь предложить Сете самому отсчитать себе зерно за зерном всю причитавшуюся ему пшеницу.

В самом деле: если бы Сета, принявшись за счет, вел его непрерывно день и ночь, отсчитывая по зерну в секунду, он в первые сутки отсчитал бы всего 86 400 зерен. Чтобы отсчитать миллион зерен, понадобилось бы не менее 10 суток неустанного счета. Один кубический метр пшеницы он отсчитал бы примерно за полгода. И осталось бы отсчитать ещё 1 499 999 999 999 м3. Вы видите, что, посвятив счету даже весь остаток своей жизни, Сета получил бы лишь ничтожную часть потребованной им награды.

Экспоненциальный рост

Стремительное возрастание значений величины, подобное тому, которое мы наблюдали, в математике называется экспоненциальным ростом.

Экспоненциальный рост – возрастание величины, когда скорость роста пропорциональна значению самой величины. Говорят, что такой рост подчиняется экспоненциальному закону. В случае дискретной области определения с равными интервалами его еще называют геометрическим ростом (значения функции образуют геометрическую прогрессию). 

Для любой экспоненциально растущей величины чем большее значение она принимает, тем быстрее растет. Также это означает, что величина зависимой переменной и скорость ее роста прямо пропорциональны.

Примером экспоненциального роста может быть рост числа бактерий в колонии до наступления ограничения ресурсов.

Экспоненциальный рост противопоставляется более медленным (на достаточно длинном промежутке времени) линейной или степенной зависимостям.

Сумма бесконечной геометрической прогрессии

Геометрическая прогрессия бывает убывающей, если знаменатель по модулю меньше единицы.

число $q^n$ при достаточно больших n может стать сколь угодно малым.
И с ростом n сумма n членов геометрической прогрессии $S_n = b_1 (1 – q^n) / (1 – q)$ становится ближе к числу $S = b_1 / (1 – q)$. (Так рассуждал, например, Ф. Виет). Число S называется суммой бесконечно убывающей геометрической прогрессии. Тем не менее, долгие века вопрос о том, какой смысл имеет суммирование ВСЕЙ геометрической прогрессии, с ее бесконечным числом членов, не был достаточно ясен математикам.

Убывающую геометрическую прогрессию можно видеть, например, в апориях Зенона «Деление пополам» и «Ахиллес и черепаха». В первом случае наглядно показывается, что вся дорога (предположим, длины 1) является суммой бесконечного числа отрезков 1/2, 1/4, 1/8 и т. д. Так оно, конечно, и есть с точки зрения представлений о конечной сумме бесконечной геометрической прогрессии. И все же – как такое может быть?

Прогрессия с коэффициентом 1/2

В апории про Ахиллеса ситуация чуть более сложная, т. к. здесь знаменатель прогрессии равен не 1/2, а какому-то другому числу. Пусть, например, Ахиллес бежит со скоростью v, черепаха движется со скоростью u, а первоначальное расстояние между ними равно l. Это расстояние Ахиллес пробежит за время l/v, черепаха за это время сдвинется на расстояние lu/v. Когда Ахиллес пробежит и этот отрезок, дистанция между ним и черепахой станет равной $l (u/v)^2$, и т. д. Получается, что догнать черепаху – значит найти сумму бесконечно убывающей геометрической прогрессии с первым членом l и знаменателем u/v. Эта сумма – отрезок, который в итоге пробежит Ахиллес до места встречи с черепахой – равен $l / (1 – u/v) = lv / (v – u)$. Но, опять-таки, как надо интерпретировать этот результат и почему он вообще имеет какой-то смысл, долгое время было не очень ясно.

От апорий Зенона один шаг до понятий предела, предельного перехода, производной и интеграла – но на этот шаг человечеству понадобилось 2000 лет. Через 300 лет после того, как это шаг сделан и подробно изложен в учебниках для средней школы, […] смотрят на апории как баран на новые ворота.

Предел складывания бумаги

Предел складывания бумаги пополам — физический феномен, суть которого состоит в том, что лист обычной бумаги размера А4 можно сложить пополам не более 7 раз. Он происходит из-за быстроты роста показательной функции.

Если бумагу сложили пополам пять раз, то количество слоёв будет два в степени пять, то есть тридцать два.

Если бумагу сложили пополам 7 раз, то количество слоёв будет два в степени 7, то есть 128.

На обычном листе А4 закон подтвердился, тогда исследователи проверили закон на огромном листе бумаги. Лист размером с футбольное поле (51,8×67,1 м) им удалось сложить 8 раз без специальных средств (11 раз с применением катка и погрузчика). По утверждению поклонников телепередачи, калька от упаковки офсетной печатной формы формата 520×380 мм при достаточно небрежном складывании без усилий складывается восемь раз, с усилиями — девять.

Уже в Древнем Египте знали не только арифметическую, но и геометрическую прогрессию. Вот, например, задача из папируса Райнда: «У семи лиц по семи кошек; каждая кошка съедает по семи мышей, каждая мышь съедает по семи колосьев, из каждого колоса может вырасти по семь мер ячменя. Как велики числа этого ряда и их сумма?»

решение.

Людей всего 7, кошек 72 = 49, они съедают всего 73 = 343 мыши, которые съедают всего 74 = 2401 колосьев, из них вырастает 75 = 16807 мер ячменя, в сумме эти числа дают 19 607.

Логарифмы членов геометрической прогрессии (если определены) образуют арифметическую прогрессию.

Задача

Найти сумму первых 20 членов:
$$2+22+222+2222+ldots$$

Решение

См. также

Учебники:
Кравчук Алгебра 9 класс, раздел 4 (с. 164)
Виленкин Алгебра 9 класс (угл) 2006, с.251 – вводятся понятия предела последовательности и математической индукции

Арифметическая прогрессия

Источник

запиши периодическую дробь (0,(8)) обыкновенной дробью.

Решение.

Достаточно очевидно, что (0,(8)=0,8+0,08+0,008+…)  Слагаемые в правой части равенства образуют бесконечно убывающую геометрическую прогрессию, первый член которой равен (0,8), знаменатель равен (0,1). Найдём сумму по  формуле:

S=b11−q=0,81−0,1

.

Осталось выполнить нужные действия с десятичными дробями:

0,81−0,1=0,80,9=89

.

Таким образом, бесконечная периодическая десятичная дробь (0,(8)) обращается в обыкновенную дробь (8/9).

Ответ: (0,(8)=8/9).

Источник

Добавить комментарий