Как найти площадь гистограммы

Гистограмма – это тип графического представления в Excel, и для его создания существуют различные методы, но вместо использования пакета инструментов анализа или из сводной таблицы мы также можем сделать гистограмму из формул, а формулы, используемые для создания гистограммы, – это ЧАСТОТА и Счетчики. формулы вместе.

Что такое формула гистограммы?

Формула для гистограммы в основном вращается вокруг площади полосок, она очень проста и вычисляется путем суммирования произведения плотности частот каждого интервала классов и ширины соответствующего интервала классов. Формула площади гистограммы математически представлена ​​как

Объяснение формулы гистограммы

Формулу для вычисления площади гистограммы можно получить, выполнив следующие семь простых шагов:

Шаг 1 : Во-первых, необходимо решить, как следует измерять процесс и какие данные следует собирать. После принятия решения данные собираются и представляются в табличной форме, например в электронной таблице.

Шаг 2: Теперь подсчитайте количество собранных точек данных.

Шаг 3 : Затем определите диапазон выборки, который представляет собой разницу между максимальным и минимальным значениями в выборке данных.

Диапазон = Максимальное значение – Минимальное значение

Шаг 4: Затем определите количество интервалов между занятиями, которые могут быть основаны на любом из следующих двух методов:

1. Как правило, используйте 10 как количество интервалов или
2. Количество интервалов можно рассчитать как квадратный корень из количества точек данных, который затем округляется до ближайшего целого числа.

Количество интервалов = 

Шаг 5: Теперь определите ширину класса интервала, разделив диапазон выборки данных на количество интервалов.

Ширина класса = Диапазон / Количество интервалов

Шаг 6: Затем создайте таблицу или электронную таблицу с частотами для каждого интервала. Затем выведите плотность частот для каждого интервала, разделив частоту на соответствующую ширину класса.

Шаг 7: Наконец, площадь для уравнения гистограммы вычисляется путем сложения произведения всей плотности частот и соответствующей им ширины класса.

Примеры формул гистограммы (с шаблоном Excel)

Давайте посмотрим на простой и продвинутый пример, чтобы лучше понять расчет уравнения гистограммы.

Вы можете скачать этот шаблон Excel с формулой гистограммы здесь – Шаблон Excel с формулой гистограммы

Формула гистограммы – Пример №1

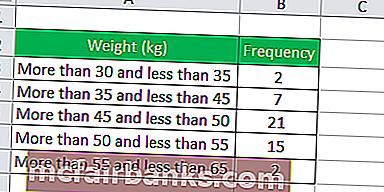
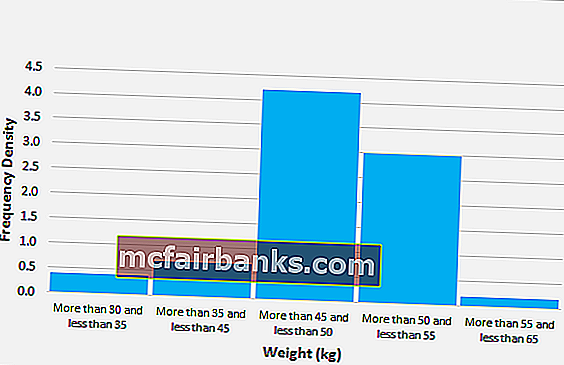
 Давайте рассмотрим приведенную ниже таблицу, в которой указаны веса детей в классе. 

Из приведенной выше таблицы можно рассчитать следующее:

• Ширина класса первого интервала = 35 – 30 = 5
• Ширина класса второго интервала = 45 – 35 = 10
• Ширина класса третьего интервала = 50 – 45 = 5
• Ширина класса четвертого интервала = 55-50 = 5
• Ширина класса пятого интервала = 65 – 55 = 10

Еще раз,

• Плотность частот первого интервала = 2/5 = 0,4
• Плотность частот второго интервала = 7/10 = 0,7
• Плотность частот третьего интервала = 21/5 = 4,2
• Плотность частот четвертого интервала = 15/5 = 3,0
• Плотность частот пятого интервала = 2/10 = 0,2

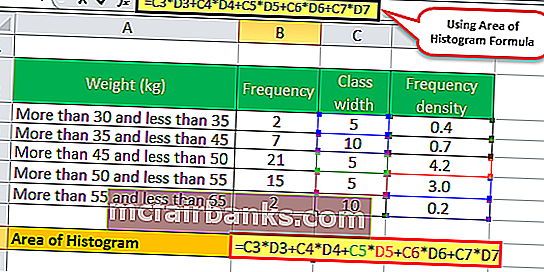
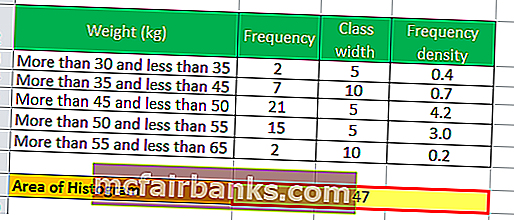
Для расчета формулы гистограммы сначала нам нужно будет вычислить ширину класса и плотность частоты, как показано выше.

Следовательно,  Площадь гистограммы = 0,4 * 5 + 0,7 * 10 + 4,2 * 5 + 3,0 * 5 + 0,2 * 10.

Итак, площадь гистограммы будет –

• Следовательно, Площадь гистограммы = 47 детей.

Графическое изображение веса детей показано ниже,

Актуальность и использование

Концепция уравнения гистограммы очень полезна, поскольку она используется для изображения набора данных. Хотя гистограмма очень похожа на гистограмму, конечное использование гистограммы сильно отличается от гистограммы. Гистограмма полезна для отображения большого количества данных в более понятном виде, который легко визуализировать. Гистограмма показывает плотность частот каждого интервала класса. Медиана и распределение данных могут быть определены с помощью гистограммы. Кроме того, можно определить асимметрию распределения, как если бы столбцы слева или справа были выше, то это указывает на то, что данные искажены, или в противном случае данные являются симметричными.

Гистограмма в первую очередь находит свое применение в случае крупномасштабных исследований, таких как общенациональная перепись, которая может проводиться каждые десять лет. В таких случаях данные компилируются и представляются в виде гистограммы, чтобы их можно было легко изучить. Кроме того, в случаях опросов, когда гистограмма создается так, чтобы любой, кто может интерпретировать гистограмму, мог использовать данные позже для дальнейших исследований или анализа.

Для
наглядности строят различные графики
статистического распределения, например,
гистограмму.

Гистограмма
частот — ступенчатая фигура, состоящая
из прямоугольников, основаниями которых
служат интервалы длиной h, а высота
которых равны отношению n_i/h, где
все наблюдаемые значения разбивают на
несколько интервалов длиною h и находят
значение n_i как сумму частот тех
вариант, которые попали в i-интервал.

Для
построения гистограммы частот на оси
абсцисс откладывают интервалы, а высота
каждого столбика равна n_i/h.

Площадь
i-прямоугольника равна = (n_i/h)
·
h , т. е.
сумме частот тех значений, которые
попали в этот i-интервал.

n_i/h
h

Площадь
всей гистограммы равна количеству
выборки n (сумме всех частот n_i)

Пример:
построить гистограмму частот распределения:
в 1м столбце указан интервал, а во 2м —
сумма частот вариант:

Интервал h	Частоты ni
2-5	9
5-8	10
8-11	25
11-14	6

Строим
еще одну колонку, в которой укажем
высоту. Как написано выше, высота у нас
равна n_i/h,
и то, и другое нам известно. Интервал
(h) равен 3 (это можно проследить: 2-5=3,
8-5=3, 11-8=3 и т. д.). Итак, строим:

Интервал h	Частоты ni	Высота ni/h
2-5	9	Равно 9:3=3
5-8	10	Равно 10:3=3,3
8-11	25	Равно 25:3=8,3
11-14	6	Равно 6:3=2

Посчитаем
сумму частот (это будет площадь
гистограммы):

складываем
все n_i =
9+10+25+6= 50

Строим
гистограмму:

8

,3

3,3

3

2

2
5 8 11 14

Ось х — интервалы.

Ось
у — высота (тот столбик, который мы
рассчитывали сами)

30. Свойства статистических оценок параметров распределения: несмещённость, эффективность, состоятельность.

Пусть
требуется изучить количественный
признак ГС. В распоряжении исследователя
имеется выборка объемом n
этого количественного признака

;

; … ;

Рассматривая
эти наблюдения как независимые случайные
величины

;

; … ;

можно сказать, что найти СТАТИСТИЧЕСКУЮ
ОЦЕНКУ НЕИЗВЕСТНОГО ПАРАМЕТРА это
значит найти функцию от наблюдаемых
значений, которая и дает приближенное
значение оцениваемого параметра.

Для
того, чтобы статистические оценки давали
хорошие приближения оцениваемых
параметров, они должны удовлетворять
некоторым требованиям.

Пусть


– статистическая оценка неизвестного
параметра

(«тета»)

1. ОПР
   – НЕСМЕЩЁННОЙ называют статистическую
   оценку
   
   математическое ожидание которой равно
   оцениваемому параметру при любом объеме
   выборки т.е.
   

   ОПР
   – СМЕЩЁННОЙ называют оценку, математическое
   ожидание которой не равно оцениваемому
   параметру.

Оценка
должна быть несмещенной.

1. ОПР
   – ЭФФЕКТИВНОЙ называют статистическую
   оценку, которая имеет наименьшую
   возможную дисперсию (при заданном
   объеме выборки n)

2. ОПР
   – СОСТОЯТЕЛЬНОЙ называют статистическую
   оценку, которая при
   
   стремится к оцениваемому параметру.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

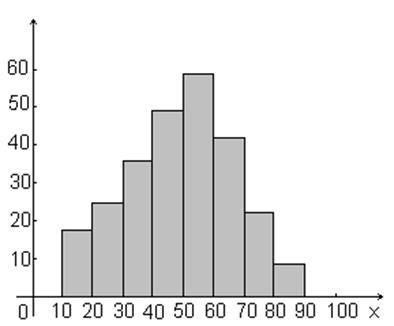
Пример 1.11 Построим
гистограмму частот статистического ряда из примера 1.7 о возрасте пациентов
поликлиники.

Рисунок 1.10 – Гистограмма частот данных

о
возрасте пациентов поликлиники

■

Иногда более полезным может
оказаться другой вид гистограммы, которая называется гистограммой
относительных частот статистического ряда. Чтобы её получить, на каждом
интервале статистического ряда строится прямоугольник, площадь которого
равна относительной частоте этого интервала. Из формулы площади прямоугольника
легко получается выражение для его высоты:

 , i =
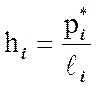
1, 2, …, k ,

где
 – относительная частота i-го 
интервала, а  –  это длина i-го
интервала.

При изображении гистограммы удобно выбирать такой масштаб,
в котором длина интервалов   равна 1. Тогда высоты
прямоугольников равны соответствующим относительным частотам: h_i = , i =
1,2, …, k.Это упрощает построение гистограммы.          В дальнейшем будем считать, что
длина каждого интервала равна 1.

Пример 1.12  Построим
гистограмму относительных частот статистического ряда из примера 1.7.

 

x

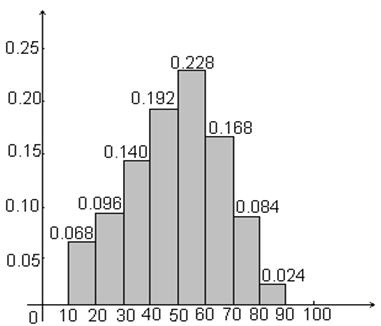
Рисунок 1.11 – Гистограмма относительных частот данных

о возрасте пациентов поликлиники

■

Подчеркнем, что форма гистограммы существенно определяется статистическим
рядом. Но любой статистический ряд является обобщением определенной выборки
значений некоторой случайной величины. Следовательно, форма гистограммы определенным
образом характеризует не только статистическое распределение выборки, но и
распределение исследуемой случайной величины. Напомним, что в теории
вероятностей закон распределения непрерывной случайной величины X определяется формулой плотности
распределения вероятностей, обозначаемой через .

Отметим важное свойство гистограммы.

Высота прямоугольника каждого интервала гистограммы относительных
частот является приближенным значением плотности распределения вероятностей
исследуемой случайной величины на этом интервале:

.

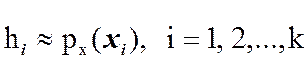
Таким
образом, верхнюю ступенчатую границу гистограммы можно считать статистическим
аналогом кривой плотности распределения непрерывной случайной величины.
Гистограмма на каждом интервале показывает средние плотности распределения
вероятностей. Если середины верхних оснований прямоугольников гистограммы
соединить прямолинейными отрезками, то получится полигон распределения частот.
Очевидно, что при увеличении числа испытаний и при уменьшении длины интервалов
ступенчатая ломаная, ограничивающая гистограмму сверху, будет более
соответствовать кривой плотности распределения. Итак, если мы сгладим верхнюю
ступенчатую ломаную гистограммы плавной кривой, то получим наглядное
представление о кривой плотности распределения вероятностей исследуемой
случайной величины. Таким образом гистограмма является удобным способом
представления сгруппированных данных.

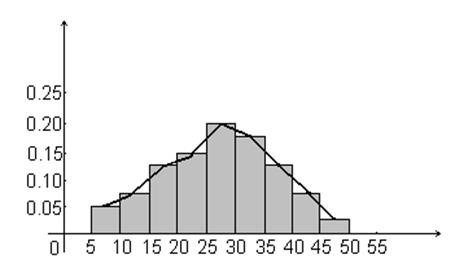
Пример 1.13 Построим гистограмму  относительных
частот статистического ряда по данным примера 1.8 о высотах городских зданий и
покажем приближенный график плотности распределения вероятностей.

Рисунок 1.12 – Гистограмма относительных частот данных

высот зданий города

■

Сформулируем ещё одно свойство гистограммы, тесно
связанное с предыдущим.

Площадь гистограммы относительных частот, построенной
на интервалах единичной длины, равна 1.

Итак,
гистограмма и полигон частот дают возможность реально увидеть в общих чертах
закономерности распределения исследуемой генеральной совокупности. Заметим, что
полигон частот имеет большее преимущество  при сравнении двух разных распределений.
В любом случае на первоначальном этапе графические формы представления
статистических данных являются важным рабочим методом статистики.

1.8 Эмпирическая функция распределения

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание – внизу страницы.

 План:

1.      Задачи математической статистики.

2.      Виды выборок.

3.      Способы отбора.

4.      Статистическое распределение выборки.

5.      Эмпирическая функция распределения.

6.      Полигон и гистограмма.

7.      Числовые характеристики вариационного ряда.

8.      Статистические оценки параметров
распределения.

9.      Интервальные оценки параметров распределения.

1.     
Задачи и методы математической статистики

Математическая статистика– это раздел математики, посвященный методам
сбора, анализа и обработки результатов статистических данных наблюдений для
научных и практических целей.

Пусть требуется
изучить совокупность однородных объектов относительно некоторого качественного
или количественного признака, характеризующего эти объекты. Например, если
имеется партия деталей, то качественным признаком может служить стандартность детали,
а количественным- контролируемый размер детали.

Иногда проводят
сплошное исследование, т.е. обследуют каждый объект относительно нужного
признака. На практике сплошное обследование применяется редко. Например, если
совокупность содержит очень большое число объектов, то провести сплошное
обследование физически невозможно. Если обследование объекта связано с его
уничтожением или требует больших материальных затрат, то проводить сплошное
обследование не имеет смысла. В таких случаях случайно отбирают из всей
совокупности ограниченное число объектов (выборочную совокупность) и подвергают
их изучению.

Основная задача
математической статистики заключается в исследовании всей совокупности по
выборочным данным в зависимости от поставленной цели, т.е. изучение
вероятностных свойств совокупности: закона распределения, числовых
характеристик и т.д. для принятия управленческих решений в условиях
неопределенности.

2.     
Виды выборок

Генеральная совокупность – это совокупность объектов, из которой производится выборка.

Выборочная совокупность (выборка) – это совокупность случайно отобранных
объектов.

Объем совокупности –
это число объектов этой совокупности. Объем генеральной совокупности
обозначается N,
выборочной – n.

Пример:

Если из 1000
деталей отобрано для обследования 100 деталей, то объем генеральной
совокупности N =
1000, а объем выборки n =
100.

При  составлении выборки можно поступить двумя
способами: после того, как объект отобран и над ним произведено наблюдение, он
может быть возвращен либо не возвращен в генеральную совокупность. Т.о. выборки
делятся на повторные и бесповторные.

Повторной называют выборку, при которой
отобранный объект (перед отбором следующего) возвращается в генеральную
совокупность.

Бесповторной называют выборку, при которой отобранный
объект в генеральную совокупность не возвращается.

На практике обычно
пользуются бесповторным случайным отбором.

Для того, чтобы по
данным выборки можно было достаточно уверенно судить об интересующем признаке
генеральной совокупности, необходимо, чтобы объекты выборки правильно его
представляли. Выборка должна правильно представлять пропорции генеральной
совокупности. Выборка должна быть репрезентативной (представительной).

В силу закона больших чисел можно утверждать,
что выборка будет репрезентативной, если ее осуществлять случайно.

Если объем
генеральной совокупности достаточно велик, а выборка составляет лишь
незначительную часть этой совокупности, то различие между повторной и
бесповторной выборками стирается; в предельном случае, когда рассматривается
бесконечная генеральная совокупность, а выборка имеет конечный объем, это
различие исчезает.

Пример:

В американском журнале
«Литературное обозрение» с помощью статистических  методов было проведено исследование прогнозов
относительно исхода предстоящих выборов президента США в 1936 году.
Претендентами на этот пост были Ф.Д. Рузвельт и А. М. Ландон. В качестве
источника для генеральной совокупности исследуемых американцев были взяты
справочники телефонных абонентов. Из них случайным образом были выбраны 4
миллиона адресов., по которым редакция журнала разослала открытки с просьбой
высказать свое отношение к кандидатам на пост президента. Обработав результаты
опроса, журнал опубликовал социологический прогноз о том, что на предстоящих
выборах с большим перевесом победит Ландон. И … ошибся: победу одержал
Рузвельт.
Этот пример можно рассматривать, как пример нерепрезентативной выборки. Дело в
том, что в США в первой половине двадцатого века телефоны имела лишь зажиточная
часть населения, которые поддерживали взгляды Ландона.

3.     
Способы отбора

На практике
применяются различные способы отбора, которые можно разделить на 2 вида:

1. Отбор не требует
расчленения генеральной совокупности на части (а) простой случайный
бесповторный; б) простой случайный повторный).

2. Отбор, при
котором генеральная совокупность разбивается на части. (а) типичный отбор;
б) механический отбор; в) серийный отбор).

Простым случайным
называют такой отбор, при котором объекты извлекаются по одному из всей
генеральной совокупности (случайно).

Типичным называют отбор, при котором объекты
отбираются не из всей генеральной совокупности, а из каждой ее «типичной»
части. Например, если деталь изготавливают на нескольких станках, то отбор
производят не из всей совокупности деталей, произведенных всеми станками, а из
продукции каждого станка в отдельности. Таким отбором пользуются тогда, когда
обследуемый признак заметно колеблется в различных «типичных» частях
генеральной совокупности.

Механическим называют отбор, при котором
генеральную совокупность «механически» делят на столько групп, сколько объектов
должно войти в выборку, а из каждой группы отбирают один объект. Например, если
нужно отобрать 20 % изготовленных станком деталей, то отбирают каждую 5-ую
деталь; если требуется отобрать 5 % деталей- каждую 20-ую и т.д. Иногда такой
отбор может не обеспечивать репрезентативность выборки (если отбирают каждый
20-ый обтачиваемый валик, причем сразу же после отбора производится замена
резца, то отобранными окажутся все валики, обточенные затупленными резцами).

Серийным называют отбор, при котором объекты
отбирают из генеральной совокупности не по одному, а «сериями», которые
подвергают сплошному обследованию. Например, если изделия изготавливаются
большой группой станков-автоматов, то подвергают сплошному обследованию
продукцию только нескольких станков.

На практике часто
применяют комбинированный отбор, при котором сочетаются указанные выше способы.

4.     
Статистическое распределение выборки

Пусть из генеральной совокупности извлечена выборка, причем значение x₁–наблюдалось
 раз,
x₂-n₂ 
раз,…  x_k – n_k
раз. n =
n₁+n₂+…+n_k– объем
выборки. Наблюдаемые значения
 называются вариантами, а
последовательность вариант, записанных в возрастающем порядке- вариационным
рядом. Числа наблюдений  
 называются
частотами (абсолютными частотами), а их отношения к объему выборки  
– относительными частотами или статистическими вероятностями.

Если количество
вариант велико или выборка производится из непрерывной генеральной
совокупности, то вариационный ряд составляется не по отдельным точечным
значениям, а по интервалам значений генеральной совокупности. Такой
вариационный ряд называется интервальным.
Длины интервалов при этом должны быть равны.

Статистическим
распределением выборки
называется перечень вариант и соответствующих им частот или относительных
частот.

Статистическое
распределение можно задать также в виде последовательности интервалов и
соответствующих им частот (суммы частот, попавших в этот интервал значений)

Точечный
вариационный ряд частот может быть представлен таблицей:

Аналогично можно
представить точечный вариационный ряд относительных частот.

Причем:

Пример:

Число букв в
некотором тексте Х оказалось равным 1000. Первой встретилась  буква «я», второй- буква «и», третьей- буква
«а», четвертой- «ю». Затем шли буквы 
«о», «е», «у», «э», «ы».

Выпишем места,
которые они занимают в алфавите, соответственно имеем: 33, 10, 1, 32, 16, 6,
21, 31, 29.

После упорядочения
этих чисел по возрастанию получаем вариационный ряд: 1, 6, 10, 16, 21, 29, 31,
32, 33.

Частоты появления
букв в тексте: «а» – 75, «е» -87, «и»- 75, «о»- 110, «у»- 25, «ы»- 8, «э»- 3,
«ю»- 7, «я»- 22.

Составим точечный
вариационный ряд частот:

Пример:

Задано
распределение частот выборки объема n
= 20.

Составьте точечный
вариационный ряд относительных частот.

Решение:

Найдем
относительные частоты:

xi	2	6	12
wi	0,15	0,5	0,35

При построении интервального
распределения существуют правила  выбора
числа интервалов или величины каждого интервала. Критерием здесь служит
оптимальное соотношение: при увеличении числа интервалов улучшается репрезентативность,
но увеличивается объем данных и время на их обработку. Разность
x_max – x_min между наибольшим и наименьшим значениями
вариант называют размахом выборки.

Для подсчета числа
интервалов k
обычно применяют эмпирическую формулу Стреджесса (подразумевая округление до
ближайшего удобного целого): k
= 1 + 3.322 lg n.

Соответственно,
величину каждого интервала h
можно вычислить по формуле
:

5.                     
Эмпирическая
функция распределения

Рассмотрим некоторую
выборку из генеральной совокупности. Пусть известно статистическое
распределение частот количественного признака Х. Введем обозначения: n_x
– число наблюдений, при которых
наблюдалось значение признака, меньшее х; n – общее число наблюдений (объем
выборки). Относительная частота события Х<х равна   
n_x/n. Если х изменяется, то изменяется и относительная частота, т.е.
относительная частота n_x/n–
есть функция от х. Т.к. она находится эмпирическим путем, то она называется
эмпирической.

Эмпирической функцией распределения
(функцией распределения выборки) называют функцию  
 ,
определяющую для каждого х относительную частоту события Х<х.

где
число вариант, меньших х,

n– объем выборки.

В отличие от эмпирической функции
распределения выборки, функцию распределения F(x)
генеральной совокупности называют теоретической функцией распределения.

Различие между эмпирической и
теоретической функциями распределения состоит в том, что теоретическая функция F(x) определяет вероятность события Х<x , а эмпирическая
функция 
F*(x) -относительную
частоту этого же события. Из теоремы Бернулли следует, что относительная
частота события Х<х , т.е
F*(x) стремится
по вероятности к вероятности F(x) этого события. Т.е.при
большом n   F*(x)
и
F(x) мало отличаются друг от друга.

Т.о. целесообразно использовать
эмпирическую функцию распределения выборки для приближенного представления
теоретической (интегральной) функции распределения генеральной совокупности.

F*(x) обладает всеми свойствами F(x).

1. Значения  
F*(x) 
  принадлежат
интервалу [0; 1].

2.
F*(x) 

– неубывающая
функция.

3. Если
– наименьшая варианта, то  

F*(x)= 0, при х 
< x₁

; если x_k
– наибольшая варианта, то 
F*(x)= 1, при х
> x_k
.

Т.е. 
F*(x)  служит для
оценки F(x).

Если выборка задана вариационным рядом, то эмпирическая
функция имеет вид:

График эмпирической функции называется кумулятой.

Пример:

Постройте эмпирическую функцию по данному распределению
выборки.

Решение:

Объем выборки n = 12 + 18 +30 = 60. Наименьшая
варианта 2, т.е.
при х <
2. Событие X<6,
( x₁= 2) наблюдалось 12 раз, т.е.
F*(x)=12/60=0,2 при 2 < x <
6. Событие Х<10, ( 

x₁=2,
x₂= 6) наблюдалось 12 + 18 = 30 раз, т.е.  F*(x)=30/60=0,5 

при 6 < x <
10. Т.к. х=10 наибольшая варианта, то F*(x) = 1 
при х>10. Искомая эмпирическая функция имеет вид: 

Кумулята:

Кумулята дает возможность
понимать графически представленную информацию, например, ответить на вопросы:
«Определите число наблюдений, при которых значение признака было меньше 6 или
не меньше 6. F*(6)=0,2

» Тогда число наблюдений, при которых
значение наблюдаемого признака было меньше 6 равно 0,2*n = 0,2*60 = 12. Число наблюдений, при
которых значение наблюдаемого признака было не меньше 6 равно (1-0,2)*n = 0,8*60 = 48.

Если задан интервальный вариационный
ряд, то для составления эмпирической функции распределения находят середины
интервалов и по ним получают эмпирическую функцию распределения аналогично
точечному вариационному ряду.

6.      Полигон и гистограмма

       Для наглядности строят различные графики
статистического распределения: полином и гистограммы

Полигон
частот- это ломаная, отрезки которой соединяют точки (
x₁
;n₁
), (
x₂
;n₂
),…, (
x_k
; n_k
), где
 – варианты,
 –
соответствующие им частоты.

Полигон
относительных частот- это ломаная, отрезки которой соединяют точки (
x₁
;w₁
), (x₂
;w₂
),…, (
x_k
;w_k
), где  
x_i–варианты,
w_i –
соответствующие им относительные частоты.

Пример:

Постройте полином относительных
частот по данному распределению выборки:

  Решение:

В случае
непрерывного признака целесообразно строить гистограмму, для чего интервал, в
котором заключены все наблюдаемые значения признака, разбивают на несколько
частичных интервалов длиной h
и находят для каждого частичного интервала n_i – сумму частот вариант,
попавших в i-ый
интервал. (Например, при измерении роста человека или веса, мы имеем дело с
непрерывным признаком).

Гистограмма
частот- это ступенчатая фигура, состоящая из прямоугольников, основаниями
которых служат частичные интервалы длиною h, а высоты равны отношению
      (плотность
частот).

Площадь i-го частичного
прямоугольника равна– сумме частот вариант i– го интервала, т.е. площадь
гистограммы частот равна сумме всех частот, т.е. объему выборки.

Пример:

Даны результаты изменения напряжения
(в вольтах) в электросети. Составьте вариационный ряд, постройте полигон и
гистограмму частот, если значения напряжения следующие: 227, 215, 230, 232,
223, 220, 228, 222, 221, 226, 226, 215, 218, 220, 216, 220, 225, 212, 217, 220.

Решение:

Составим вариационный ряд. Имеем n = 20, x_min=212
, x_max=232
.

Применим формулу
Стреджесса для подсчета числа интервалов.

.

Интервальный вариационный ряд
частот имеет вид:

		Плотность частот
212-216	3	0,75
216-220	3	0,75
220-224	7	1,75
224-228	4	1
228-232	3	0,75

Построим гистограмму частот:

Построим полигон частот, найдя предварительно середины
интервалов:

Гистограммой относительных
частот называют ступенчатую фигуру, состоящую из прямоугольников ,
основаниями которых  служат частичные
интервалы длиною h, а
высоты равны отношению  w_i/h 

(плотность
относительной частоты).

Площадь i-го частичного прямоугольника равна  
  – относительной частоте вариант, попавших в i– ый интервал. Т.е. площадь
гистограммы относительных частот равна сумме всех относительных частот, т.е.
единице.

7.                     
Числовые
характеристики вариационного ряда

Рассмотрим основные характеристики генеральной и выборочной
совокупностей.

Генеральным средним  
называется среднее
арифметическое значений признака генеральной совокупности. 

Для различных значений x₁, x₂
, x₃
, …, x_n. 
признака
генеральной совокупности объема N
имеем:

Если
значения признака имеют соответствующие частоты N₁
+N₂
+…+N_k
=N,
то

Выборочным средним  называется среднее арифметическое значений
признака выборочной совокупности.

Для различных значений x₁, x₂
, x₃, …, x_n 
признака выборочной
совокупности объема n
имеем:

Если
значения признака имеют соответствующие частоты n₁+n₂+…+n_k
= n,
то

Пример:

Вычислите выборочное среднее для выборки :
x₁= 51,12;
x₂= 51,07; 

x₃= 52,95; x₄
=52,93; 

x₅= 51,1;x₆
= 52,98; x₇
= 52,29; x₈
= 51,23; x₉
= 51,07; x₁₀
= 51,04.

Решение:

Генеральной дисперсией называется среднее арифметическое квадратов отклонений
значений признака Х генеральной совокупности от генерального среднего .

Для различных значений x₁, x₂, x₃, …, x_N 
признака
генеральной совокупности объема N
имеем:

Если
значения признака имеют соответствующие частоты
N₁+N₂+…+N_k
=N,
то

Генеральным среднеквадратическим отклонением (стандартом)
называют квадратный корень из генеральной дисперсии

Выборочной дисперсией    называется среднее
арифметическое квадратов отклонений наблюдаемых значений признака от среднего
значения.

Для различных значений
x₁, x₂, x₃, …, x_n
признака выборочной
совокупности объема n
имеем:

Если
значения признака имеют соответствующие частоты n₁+n₂+…+n_k
= n,
то

Выборочным среднеквадратическим
отклонением (стандартом) называется квадратный корень из выборочной
дисперсии.

Пример:

Выборочная совокупность задана таблицей распределения. Найдите
выборочную дисперсию.

Решение:

Теорема: Дисперсия
равна разности среднего квадратов значений признака и квадрата общего среднего.

Пример:

Найдите дисперсию по данному распределению.

Решение:

8.      Статистические оценки параметров распределения

Пусть генеральная совокупность исследуется по некоторой
выборке. При этом можно получить лишь приближенное значение неизвестного
параметра Q, который
служит его оценкой. Очевидно, что оценки могут изменяться от одной выборки к
другой.

Статистической
оценкой Q* неизвестного параметра
теоретического распределения называется функция f, зависящая от наблюдаемых значений
выборки. Задачей статистического оценивания неизвестных параметров по выборке
заключается в построении такой функции от имеющихся данных статистических
наблюдений, которая давала бы наиболее точные приближенные значения реальных,
не известных исследователю, значений этих параметров.

Статистические оценки делятся на
точечные и интервальные, в зависимости от способа их предоставления (числом или
интервалом).

Точечной
называют статистическую оценку параметра Q теоретического распределения определяемую одним значением
параметра Q*=f(x₁, x₂, …, x_n), где x₁, x₂, …, x_n – результаты эмпирических наблюдений над
количественным признаком Х некоторой выборки.

Такие оценки параметров, полученные по
разным выборкам, чаще всего отличаются друг от друга. Абсолютная разность /Q*-Q/ называют ошибкой выборки (оценивания).

Для того, чтобы статистические оценки
давали достоверные результаты об оцениваемых параметрах, необходимо, чтобы они
были несмещенными, эффективными и состоятельными.

Точечная
оценка, математическое ожидание которой равно (не равно) оцениваемому
параметру, называется несмещенной
(смещенной). М(Q*)=Q.

Разность М(Q*)-Q называют смещением или
систематической ошибкой. Для несмещенных оценок систематическая ошибка
равна 0.

Эффективной
называют такую статистическую оценку
Q*, которая при
заданном объеме выборки n
имеет наименьшую возможную дисперсию: D[Q*]min
(n=const). Эффективная оценка
имеет наименьший разброс по сравнению с другими несмещенными и состоятельными
оценками.

Состоятельной
называют такую статистическую оценку
Q*,
которая при n стремится по вероятности к оцениваемому
параметру Q,
т.е. при увеличении объема выборки n
оценка стремится по вероятности к истинному значению параметра Q.

Требование состоятельности
согласуется с законом больших числе: чем больше исходной информации об
исследуемом объекте, тем точнее результат. Если объем выборки мал, то точечная
оценка параметра может привести к серьезным ошибкам.

Любую выборку (объема n) можно рассматривать
как упорядоченный набор
x₁, x₂, …, x_n независимых
одинаково распределенных случайных величин.

Выборочные средние для
различных выборок объема n из одной и той же генеральной
совокупности будут различны. Т. е. выборочное среднее можно рассматривать как
случайную величину, а значит, можно говорить о распределении выборочного
среднего и его числовых характеристиках.

Выборочное среднее
удовлетворяет всем накладываемым к статистическим оценкам требованиям, т.е.
дает несмещенную, эффективную и состоятельную оценку генерального среднего.

Можно доказать, что. Таким образом, выборочная дисперсия
является смещенной оценкой генеральной дисперсии, давая ее заниженное значение.
Т. е. при небольшом объеме выборки она будет давать систематическую ошибку. Для
несмещенной, состоятельной оценки достаточно взять величину
, которую называют исправленной
дисперсией. Т. е.

  На практике для оценки генеральной дисперсии применяют исправленную
дисперсию при n
< 30. В остальных случаях (n>30) отклонение
 от

 малозаметно. Поэтому при больших значениях n
ошибкой смещения можно пренебречь.

Можно
так же доказать,  что относительная
частота
n_i / n является
несмещенной и состоятельной оценкой вероятности P(X=x_i). Эмпирическая функция распределения F*(x) является несмещенной
и состоятельной оценкой теоретической функции распределения F(x)=P(X<x).

Пример:

Найдите
несмещенные оценки математического ожидания 
и дисперсии по таблице выборки.

Решение:

Объем выборки n=20.

Несмещенной оценкой математического
ожидания является выборочное среднее.

Для вычисления несмещенной оценки
дисперсии сначала найдем выборочную дисперсию:

  Теперь найдем
несмещенную оценку:

9.                     
Интервальные
оценки параметров распределения

Интервальной называется статистическая
оценка, определяемая двумя числовыми значениями- концами исследуемого
интервала.

Число> 0, при котором |Q–Q*|<
, характеризует точность интервальной
оценки.

Доверительным
называется интервал
, который с заданной вероятностью  покрывает неизвестное значение параметра Q. Дополнение
доверительного интервала до множества всех возможных значений параметра Q называется критической областью. Если критическая
область расположена только с одной стороны от доверительного интервала, то
доверительный интервал называется односторонним:
левосторонним, если критическая область существует только слева, и правосторонним- если только справа. В
противном случае, доверительный интервал называется двусторонним.

Надежностью,
или доверительной вероятностью, оценки Q (с помощью Q*) называют вероятность,
с которой выполняется следующее неравенство: |Q–Q*|<
.

Чаще всего доверительную вероятность
задают заранее (0,95; 0,99; 0,999) и на нее накладывают требование быть близкой
к единице.

Вероятность
 называют вероятностью
ошибки, или уровнем значимости.

Пусть |Q–Q*|<

, тогда

. Это означает, что с вероятностью
 можно утверждать, что истинное значение
параметра Q
принадлежит интервалу. Чем меньше величина отклонения
, тем точнее оценка.

Границы (концы) доверительного интервала
называют доверительными границами, или
критическими границами.

Значения границ доверительного интервала
зависят от закона распределения параметра Q*.

Величину отклонения
равную половине ширины доверительного
интервала, называют точностью оценки.

Методы построения доверительных
интервалов впервые были разработаны американским статистом Ю. Нейманом.
Точность оценки
, доверительная вероятность  
и
объем выборки n связаны между собой. Поэтому, зная
конкретные значения двух величин, всегда можно вычислить третью.

Нахождение
доверительного интервала для оценки математического ожидания нормального
распределения, если известно среднеквадратическое отклонение.

Пусть произведена выборка из генеральной
совокупности, подчиненной закону нормального распределения. Пусть известно
генеральное среднеквадратическое отклонение
, но неизвестно математическое ожидание
теоретического распределения a
().

Справедлива следующая формула:

Т.е.
по заданному значению отклонения
 можно найти, с какой вероятностью неизвестное
генеральное среднее принадлежит интервалу. И наоборот. Из формулы видно, что при
возрастании объема выборки и фиксированной величине доверительной вероятности
величина
–
уменьшается, т.е. точность оценки увеличивается. С увеличением надежности
(доверительной вероятности), величина
 -увеличивается,
т.е. точность оценки уменьшается.

Пример:

В результате испытаний
были получены следующие значения -25, 34, -20, 10, 21. Известно, что они
подчиняются закону нормального распределения с среднеквадратическим отклонением
2. Найдите оценку а* для математического ожидания а. Постройте для него 90%-ый
доверительный интервал.

Решение:

Найдем несмещенную
оценку  

Тогда

Доверительный интервал
для а имеет вид: 4 – 1,47< a
< 4+ 1,47 или 2,53 < a
< 5, 47

Нахождение
доверительного интервала для оценки математического ожидания нормального
распределения, если неизвестно среднеквадратическое отклонение.

Пусть известно, что генеральная
совокупность подчинена закону нормального распределения, где неизвестны а и
. Точность доверительного интервала,
покрывающего с надежностью  
 истинное значение параметра а,  в данном случае вычисляется по формуле:

, где n– объем выборки,
,– коэффициент Стьюдента (его следует
находить по заданным значениям n и
 из
таблицы «Критические точки распределения Стьюдента»).

Пример:

В результате испытаний были получены
следующие значения -35, -32, -26, -35, -30, -17. Известно, что они подчиняются
закону нормального распределения. Найдите доверительный интервал для
математического ожидания а генеральной совокупности с доверительной вероятностью
0,9.

Решение:

Найдем несмещенную оценку
.

Найдем
 .

Далее найдем  
.

Тогда

Доверительный интервал примет вида (-29,2
– 5,62; -29,2 + 5,62) или (-34,82; -23,58).

Нахождение
доверительного интерла для дисперсии и среднеквадратического отклонения
нормального распределения

Пусть из некоторой генеральной
совокупности значений, распределенной по нормальному закону, взята случайная
выборка объема n <
30, для которой вычислены выборочные
дисперсии: смещенная
 и
исправленная s²
. Тогда для нахождения интервальных
оценок с заданной надежностью
  для генеральной дисперсии D генерального
среднеквадратического отклонения
 используются следующие формулы.

или   
,
 

Значения
– находят с помощью таблицы значений
критических точек распределения
Пирсона.

Доверительный интервал для дисперсии
находится из этих неравенств путем возведения всех частей неравенства в
квадрат.

Пример:

Было проверено качество 15 болтов.
Предполагая, что ошибка при их изготовлении подчинена нормальному закону
распределения, причем выборочное среднеквадратическое отклонение
равно 5 мм, определить с надежностью доверительный интервал для неизвестного
параметра
.

Решение:

Т. к. n = 15 <30, то воспользуемся формулой
.

Найдем пограничные значения вероятности
для .

Тогда:

Границы интервала представим в виде  двойного неравенства:

Концы двустороннего доверительного
интервала для дисперсии можно определить и без выполнения арифметических
действий по заданному уровню доверия и объему выборки с помощью соответствующей
таблицы (Границы доверительных интервалов для дисперсии в зависимости от числа
степеней свободы и надежности). Для этого полученные из таблицы концы интервала
умножают на исправленную дисперсию s²
.

Пример: 

Решим предыдущую задачу другим способом.

 Решение:

Найдем исправленную
дисперсию:

По таблице «Границы
доверительных интервалов для дисперсии в зависимости от числа степеней свободы
и надежности» найдем границы доверительного интервала для дисперсии при k=14 и
: нижняя граница 0,513 и верхняя 2,354.

Умножим полученные
границы на
s² и
извлечем корень (т.к. нам нужен доверительный интервал не для дисперсии, а для
среднеквадратического отклонения).

Как видно из примеров,
величина доверительного интервала зависит от способа его построения и дает
близкие между собой, но неодинаковые результаты.

При выборках достаточно
большого объема (n>30)
границы доверительного интервала для генерального среднеквадратического
отклонения можно определить по формуле:

Существует и другой
способ определения границы доверительного интервала для дисперсии, в основе
которого лежит выбор интервала, симметричного относительно
:

Причем
 –
некоторое число, которое табулировано и приводится в соответствующей справочной
таблице.

Если 1- q<1, то формула имеет
вид: 

Пример:

Решим предыдущую задачу третьим способом.

 Решение:

Ранее было найдено s
= 5,17. q(0,95;
15) = 0,46 – находим по таблице.

Тогда: