Вычисление
площадей графическим способом состоит
в том, что участки, изображенные на
плане, разбивают на простейшие
геометрические фигуры – преимущественно
на треугольники, реже трапеции и
прямоугольники. В каждой фигуре на плане
измеряют высоту и основание, по которым
вычисляется площадь. Сумма площадей
фигур дает площадь участка.
Чем
меньше углов имеет граница участка, тем
меньше эффективность этого способа,
следовательно, для вычисления площадей
участков, имеющих большое количество
углов, целесообразнее вычислять площадь
по графическим координатам точек, т.е.
по координатам, измеренным на плане при
помощи измерителя или координатографа,
координатометра и др., пользуясь формулами
(6.6), (6.7).
Наилучшим
вариантом разбивки участка на треугольники
будет тот, при котором треугольники
близки к равносторонним (вернее, высоты
по величине близки основаниям).
При
разбивке участка на простейшие фигуры
можно принять много вариантов, однако,
точность вычисления площади участка
при различных вариантах не будет
одинаковой. Погрешность вычисления
площади каждого треугольника по высоте
и основанию можно рассчитать по формуле
(6.8).
Эта формула
справедлива также для прямоугольника,
параллелограмма и трапеции, площади
которых вычисляют по двум величинам,
измеренным по плану.
Погрешности
измерения линий по плану можно считать
одинаковыми, независимо от длин линий,
т.е. mа =
mh =
m.
Тогда по формуле
(6.8)
.
(6.9)
Так
для треугольника
,
а для остальных фигур
,
то согласно (6.9), для треугольника
,
(6.10)
а для прямоугольника,
параллелограмма и трапеции
,
(6.11)
Если
a=h,
то для ∆
.
(6.12)
Для
прямоугольника и параллелограмма (при
a1=h1),
а также трапеции при равенстве средней
линии и высоты
.
Таким
образом, площадь треугольника графическим
способом вычисляется точнее, чем площади
других фигур, следовательно, площадь
при разбивке на треугольники вычисляется
точнее, чем при разбивке на прямоугольники,
трапеции и др.
Учитывая,
что при разбивке фигуры на треугольники
не всегда можно получить треугольники
с одинаковыми основаниями и высотами
погрешность площади участка можно
вычислить по формуле
или для планов
разных масштабов
,
где М- знаменатель
численного масштаба плана.
Определение
площади с помощью параллельной палетки.
Если
участок имеет криволинейную границу и
его площадь на
плане менее 10 см, то ее можно измерить
палеткой, которая представляет
собой ряд параллельных линий, проведенных
через интервалы
h
=2
мм на любой прозрачной основе (кальке,
пластиковой
пленке и др.).
Для
определения площади палетку накладывают
на план как показано на (рис.
6.2), чтобы крайние точки контура участка
1 и 16 находились посредине
между линиями палетки. В результате
участок расчленяется
на отдельные трапеции с высотой h
и
средними линиями
S2-3,
S3-4,…,
S14-15,
которые
измеряют в масштабе плана (основания
трапеций
изображены на рис. 6.2 пунктиром). Так как
площадь каждой
трапеции равна
,
то
общая площадь участка
.

Рис.6.2 Измерение
площади с помощью параллельной палетки
Сумму
расстояний
последовательно
набирают в раствор
измерителя:
взяв расстояние S2-3,
переносят левую углу измерителя в
точку 5, а правую устанавливают на
продолжении линии 4—5
в
точке k,
после
чего увеличивают раствор измерителя
перемещением
левой иголки в точку 4.
Тогда
в растворе измерителя 4—k
будет
набрана сумма средних линий (S2-3+S4-5).
Дальнейшие измерения
продолжают в той же последовательности.
Если в процессе
набора расстояний раствор измерителя
окажется больше размера
палетки по ее длине AB,
то
сумму средних линий набирают
по частям в несколько приемов. Общую
длину измеренных
средних линий определяют по масштабной
линейке и умножают на
высоту h,
соответствующую
числу метров в масштабе плана. Полученную
площадь выражают в гектарах.
Точность
однократного определения площади
квадратной и параллельной палетками
определяется по формуле
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- Определение площади участков графическим способом
- Способы определения площади земельного участка
- Основные способы
- Аналитический способ
- Графический метод
- Механический способ
- Погрешность определения площади
- Определение площади участка на ПКК
Определение площади участков графическим способом



Графический способ определения площадей состоит в том, что участки, изображённые на плане, разбивают на треугольники, в которых высоты по величине близки к основаниям. Зная высоту и основание, вычисляют площадь.
Для контроля и повышения точности вычислений площадь каждого треугольника определяют дважды: по двум различным основаниям и высотам. Допустимость расхождения между двумя значениями площади определяют по формуле
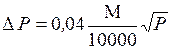
где М — знаменатель численного масштаба плана;
Р — площадь треугольника, га.
Для определения площадей небольших криволинейных участков применяют палетки.
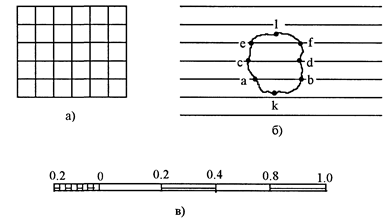
Квадратная палетка (рисунок 4а) — это сетка квадратов со сторонами 1-2 мм. Площадь участка определяется подсчётом квадратов палетки, наложенной на фигуру. Рекомендуется при определении площадей участков не более 2 см 2 на плане.
Параллельная палетка (рисунок 4б) — это ряд параллельных линий, проведённых на расстоянии 2 мм. Палетку накладывают на участок так, чтобы крайние её точки k и l были расположены между её линиями. Измерив, средние линии трапецией ab, cd, ef в масштабе плана и умножив их сумму на расстояние между линиями палетки, получают площадь участка. Рекомендуется при определении площадей до 10 см 2 на плане.
Чтобы не выполнять вычислений строят специальную шкалу — масштабную палетку (рисунок 4в), по которой определяют площадь участка, зная сумму средних линий. Рассчитаем основание шкалы для масштаба 1:10000. При расстоянии между параллельными линиями 2 мм и при длине шкалы 1 см площадь будет равна 20 ´ 100 = 2000 м 2 = 0,20 га. Следовательно, каждому сантиметру шкалы будет соответствовать 0,20 га на местности. Левое основание шкалы делят на 10 частей. После того как сумма средних линий набрана в раствор циркуля, определяют площадь по шкале так же, как расстояние по линейному масштабу.
Точность однократного определения площадей квадратной и параллельной палетками в среднем характеризуется формулой
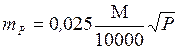
где М — знаменатель численного масштаба плана;
Р — площадь фигуры, га.
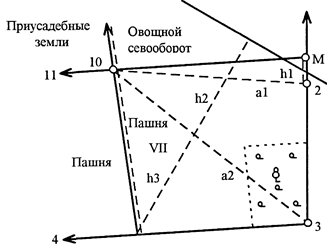
2.2.1 В соответствии с рисунком 5 определить графическим способом площадь пашни восточной части поля VII.
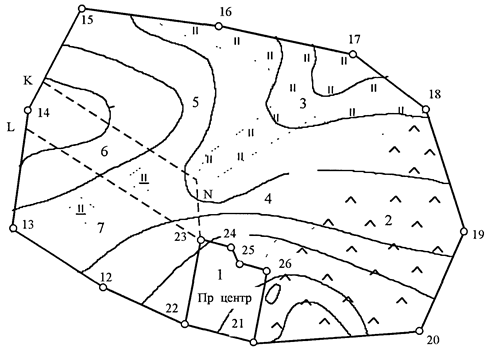
Площадь пашни восточной части поля VII вычислить по формуле
2.2.2 Построить параллельную и масштабную палетки для масштаба плана и, пользуясь ими, определить площади прудов в северной и южной части землепользования.
2.3 Определение площадей участков механическим способом
2.3.1. Определение цены деления планиметра
Выполнив поверку основного геометрического условия планиметра, определяем цену деления планиметра путем обвода двух квадратов координатной сетки, по два обвода при каждом положения полюса. Цену деления планиметра определяем по формуле
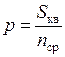
где S — площадь квадратов координатной сетки;
n ср — среднее значение разности отсчетов.
Цену деления p выражают четырьмя-пятью значащими цифрами в зависимости от величины первой цифры
2.3.2. Составление кальки контуров
Разделить массив пашни в северной части землепользования на участки в соответствии с рисунком 6, при этом границы между ними провести карандашом (линии NK и 23 — L параллельны линии 13 — 12), обозначить номера контуров. Вкрапленные контуры обозначить тем же номером, что и основной контур с добавлением индекса “а”, “б” и т.д.
2.3.3. Определение площадей контуров планиметром.
Определить площадь каждого контура двумя обводами планиметра при одном положении счётного механизма.
Площади вкрапленных контуров определить планиметром способом повторений (3-4 повторения), снимая отчеты перед первым обводом и после последнего; разность отчётов разделить на число обводов.
Площади участков угодий вычислить по среднему значению цены деления планиметра , округляя значения площадей до 0.01 га.
Невязку определить по формуле fp = å Рвыч — Ртеор и сравнить её с допустимой
где р — цена деления планиметра;
n — число контуров, площади которых определяют планиметром;
М — знаменатель численного масштаба плана;
Р — общая площадь участка.
Если невязка допустима, распределить её с обратным знаком пропорционально площадям угодий.

Результаты вычислений сводим в таблицу 2.
Таблица 2 — Ведомость вычисления площадей планиметром
Источник
Способы определения площади земельного участка
При проведении землеустроительных работ используются различные способы вычисления площадей участков земли. Применение этих способов зависит от ценности этих участков, их величины, формы границ, наличия и точности данных измерений на местности, наличия карт необходимой точности и планов участков.
Основные способы
Существует три основных способа определения площадей:
- аналитический;
- графический;
- механический.

Для графического способа используются данные измерений на плане и карте.
Такой способ чаще всего используется при отсутствии информации полевых измерений.
При механическом способе площадь определяется по плану с помощью специального устройства — планиметра.
Иногда используется комбинированный способ определения площади. Например, общая площадь участка определяется по координатам характерных точек аналитическим способом, а площади внутренних участков определяются по плану с помощью графического или механического методов.
Эти три метода имеют различные показатели точности.
Точности других методов, использующих топографическую информацию с планов, зависят еще и от погрешностей приборов, качества плана, масштаба, деформации бумаги.
 Аналитический способ
Аналитический способ
Аналитический способ позволяет по координатам характерных точек границ участка определить его площадь. При этом используются формулы аналитической геометрии.
В соответствии с ними площадь многоугольника S может быть определена по формуле:
- Xi и Yi — координаты i-той характерной точки участка, имеющего вид многоугольника;
- i — порядковый номер характерной точки ЗУ. Этот параметр меняется от 1 до n;
- n — число характерных точек.
Если участок имеет четырехугольную форму, то, в общем случае, для него расчет площади производится по приведенной выше формуле с учетом того, что n=4.
Если участок имеет форму трапеции и известны его стороны, то площадь такого участка можно определить по формуле:
- a и b — основания фигуры;
- h – высота трапеции.
При расчете четырехугольника неправильной формы, когда известны размеры его сторон, вначале определяют величину полупериметра p:
a,b,c,d — величины сторон.
Тогда площадь участка Sу будет равна:
При этом по контуру границ участка производится замер азимута каждой характерной точки. Также определяется расстояние от одной характерной точки до следующей за ней точки. Вся эта информация в дальнейшем вводится в ЭВМ, которая по специальной программе производит расчет площади ЗУ.
 Графический метод
Графический метод
При расчете площади участка графическим методом чаще всего изображенный на плане участок сложной формы делят на участки элементарного вида (треугольники, прямоугольники, трапеции), затем вычисляют и суммируют площади этих фигур.
Точность графического метода зависит от точности графического измерения на плане. Известно, что точность измерения с помощью циркуля постоянна и равна 0,1 мм. Поэтому относительная ошибка при измерении коротких линий больше, чем при измерении длинных линий. В связи с этим желательно, чтобы простые фигуры были больших размеров и с близкими по размерам основаниями и высотами.
Такой метод удобен в случае, когда имеется небольшое количество характерных точек. В противном случае целесообразнее определять площадь участка по координатам точек, измеренных на плане.
Палетка представляет собой прозрачный лист, на который нанесены деления. Этот лист накладывается на план участка. Сосчитав количество делений, входящих в контур участка, и определив площадь одного деления с учетом масштаба, можно оценить площадь участка.
Недостаток такого графического метода состоит в том, что количество неполных квадратов приходится оценивать на глаз. В результате этого ухудшается точность данного метода.
Механический способ
Механический способ используется в тех случаях, когда по плану необходимо оценить площадь большого участка со сложными границами. Для осуществления этого метода используются планиметры.
Планиметр представляет собой прибор, который позволяет определить площадь плоской фигуры путем обвода ее контура. Он состоит из двух рычагов и каретки со счетным механизмом. На полюсном рычаге имеется игла, которая втыкается в план и является полюсом. Вокруг полюса по контуру участка движется обводной шпиль.
Точность метода зависит от размеров участка и свойств плана.
Погрешность определения площади
При определении площадей участков возникают неточности, которые характеризуются погрешностями. Погрешность — это разность между вычисленной величиной площади участка и ее истинной величиной.
Для различных методов определения площади такие погрешности могут быть различными.
Для аналитического метода точность расчета площади зависит исключительно от погрешностей, связанных с измерением координат поворотных точек. При этом, средняя квадратическая погрешность (СКП) аналитического метода расчета (mp) определяется формулой:
- mt — СКП расположения поворотных точек;
- P — площадь участка.
Для примера можно взять допустимые при межевании точности mt, которые определены соответствующими нормативными актами (например, Приложением к приказу МЭР № 518). Эти точности зависят от типа земель.
Так, для населенных пунктов этот показатель равен 10 см, а для дачных участков и садоводств-20 см. Таким образом, для садового участка в 600 кв. м точность определения площади аналитическим методом может составить:
При реализации графического метода на его точность влияют погрешности измерений, погрешности составления плана, деформация бумаги. Относительная погрешность такого метода составляет от 1:500 до 1:1000.
Точность механического метода также зависит от погрешностей составления плана (или карты), состояния бумаги, на которой нанесен план участка. Кроме того, на точность этого метода влияет размер участка. Этот метод не рекомендуется применять для участков размером менее 10-12 см2.
В благоприятных условиях относительная погрешность измерений площади планиметром может достигать 1:400.
При покупке квартиры можно получить налоговый вычет. Подробнее об этом читайте в нашей статье.
Хотите оформить в собственность участок, взятый в аренду на 49 лет? Здесь есть подробная инструкция.
Определение площади участка на ПКК
Публичная кадастровая карта (ПКК) — это онлайн-сервис, с помощью которого любой гражданин может узнать основные характеристики любого земельного участка, помещенные в кадастр недвижимости (ЕГКН).
Для того, чтобы узнать величину площади с помощью ПКК, надо зайти на страницу http://pkk5.rosreestr.ru и найти участок на карте. Для этого используется специальное меню, которое позволяет определить участок по кадастровому номеру, адресу.
Так, введя в поисковую систему ПКК адрес участка, можно получить его расположение на карте и некоторые данные.
Необходимо отметить, что не все участки земли можно таким образом найти по адресу. Например, при нахождении участка c кадастровым номером 50:38:0050302:130 в таблице его параметров указан адрес: «обл. Московская, р-н Зарайский, снт «Изобретатель», уч-к 116″.

Это говорит о том, что система поиска земельного участка на ПКК по адресу не до конца отработана Росреестром.
Чтобы определить площадь участка по координатам, вначале необходимо узнать эти координаты. Если участок уже найден на карте, то приблизительные координаты характерных точек можно определить, подводя к ним курсор. По этим координатам, в дальнейшем, можно определить площадь участка по формуле для аналитического метода.
Более точно координаты характерных точек участка можно узнать только при платном заказе выписки из ЕГРН для этого участка.
По новому закону в связи с объединением баз данных ЕГРП и ЕГРН такая выписка с 1.01 2017 года заменяет собой свидетельство на объект недвижимости, кадастровый паспорт, кадастровую выписку и выписку из ЕГРП. То есть, выписка из ЕГРН является основным документом на недвижимость.
Источник
Тема 2.3. Определение площадей
1.
Методы определения площадей
1.1.
Аналитический метод определения площадей.
1.2.
Графический метод определения площадей.
1.3.
Способ палетки.
1.4.
Механический метод определения площадей.
ПЛОЩАДЬ
ЛЮБОЙ ФИГУРЫ ЛЮБЫМ СПОСОБОМ ВЫЧИСЛЯЕТСЯ НЕ МЕНЕЕ ДВУХ РАЗ
Определение
площадей в землеустроительном производстве имеет большое практическое значение.
Размеры площадей надо знать с большой точностью при составлении
землеустроительных проектов, при выделении участков в пользование, а так же для
учета и использования земель в различных отраслях с/х и промышленного
производства. В зависимости от способа получения данных, с помощью которых
вычисляются площади, существует несколько методов определения площадей.
1.1.
Аналитический метод определения площадей.
Аналитический
метод состоит в определении площади участка по результатам непосредственных
измерений линий и углов в натуре или по координатам вершин (граничных точек). Точность
величины площади участка при этом зависит только от ошибок измерения длин и
углов на местности и характеризуется относительной ошибкой 1/500 – 1/1000.
Однако в условиях большой контурности и вкрапливаний одних контуров в другие,
площади которых определяются менее точными способами, аналитический метод становится
нецелесообразен.
А)
Определение площади участка по результатам измерения в натуре.
Площади
небольших участков, имеющих форму элементарных геометрических фигур, вычисляют
математически по формулам геометрии.
 |
а S = a2
в
а
S = a*в

2 S = a*h; или S
= a*h/2
a

S = ((a+в)/2)*h
или S = m*h
в
Б)
Вычисление площади полигона по координатам его вершин.
Площадь
любой фигуры ограниченной прямыми линиями можно вычислить по двум формулам.
Удвоенная
площадь полигона равна сумме произведений абсциссы каждой точки на разность
ординат последующей и предыдущей точек.
Она
же (удвоенная площадь) равна сумме произведений каждой ординаты на разность абсцисс
предыдущей и последующей точек.
2S
= x1(y2-y3)+x2(y3-y1)+x3(y1-y2)
2S
= y1(x3-x2)+y2(x1-x3)+y3(x2-x1)
2 (x2,
y2)
 |
1(x1,
y1)
3 (x3,
y3)
1.2.
Графический метод определения площадей.
Графический
метод заключается в том, что данные для вычисления площадей берутся с плана,
графически, и площади отдельных геометрических фигур вычисляются с помощью
геометрических формул.
Если
участок представляет собой многоугольник, то его делят на треугольники,
прямоугольники или трапеции. С помощью измерителя и масштабной линейки
определяют те величины, которые нужны для получения площадей отдельных фигур.
Сумма площадей элементарных геометрических фигур даст общую площадь участка.

определения площади графическим способом зависит от графической ошибки
измерения отрезка на плане. Отрезок на плане циркулем – измерителем
определяется с ошибкой +0,1мм, которая не зависит от длины линии. Из этого
следует, что относительная ошибка короткой линии больше, а длинной – меньше.
Правила
для определения площади графическим способом:
1. Площади
определяются дважды (либо участок разбивается на другие элементарные фигуры,
либо в треугольниках изменяются основания и высота).
2. План
берется в наиболее крупном масштабе.
3. Фигуры
должны быть как можно крупнее и не очень вытянуты, то есть основание и высота
должны быть примерно равны.
4. Если
в геометрических фигурах есть линии, величины которых известны из
непосредственных измерений, то их надо использовать для вычисления площадей.
5. Предельное
расхождение двукратных определений не должно превышать1:200 величины площади
участка.
При
работе по этому способу применяют специальные палетки для проведения высот.
Графически
вычисляют площади контуров имеющих вытянутую форму (дорога, канал, ручей и
т.д.), ширина которых не всегда выражается в масштабе плана, но она должна быть
известна или подписана на плане.
1.3.
Определение площади палеткой
Квадратная
палетка. Квадратная палетка представляет собой
прозрачный лист целлулоида, стекла или восковки, на котором нанесена сеть
квадратов со сторонами от 1 до 10 мм (рис. 180). Зная сторону квадрата, легко
подсчитать площадь его применительно к любому масштабу плана. Для определения
площади палетку накладывают на контур ABCD, имеющийся на плане. Вначале
подсчитывают число полных квадратов. На рис. 180 их оказалось 22, а затем
неполные квадраты объединяют и глазомерно заменяют некоторым числом полных.
Пусть таких квадратов девять. Общее число полных квадратов на площади ABCD
будет 31. Произведение площади одного квадрата на число их даст площадь
определяемого участка. Точность определения площади квадратной палеткой не
превышает 1:100.
Палетки
с параллельными линиями. Палетка с параллельными
линиями отличается от квадратной тем, что вместо квадратов на ней наносятся
параллельные линии. Она также делается из прозрачного целлулоида, на котором
нанесены параллельные линии с интервалом в 2 мм. Система таких линий с нужными
интервалами может быть нанесена на восковку. Это будет тоже палетка (рис. 181).
Для определения площади участка палетку накладывают на контур плана так, чтобы наиболее
удаленные друг от друга точки, например MN, приходились на середину расстояния
между какими-либо параллельными линиями. В результате этого площадь
определяемого контура будет разбита на трапеции, у которых сплошные линии а1
в1; а2 в2; а3 в3 и
т. д. будут средними линиями трапеций, а пунктирные (на палетке отсутствуют) —
основаниями трапеций.
Так
как высоты трапеций одинаковы и заранее известны, то для получения площади
контура надо измерить циркулем средние линии трапеций а1 в1;
а2 в2; а3 в3 т. д. Произведение
суммы средних линий на расстояние между нитями даст общую площадь контура.
Конечно, при этом надо учитывать масштаб плана.
Чтобы
не производить вычислений, ниже палетки наносят шкалу в виде простого линейного
масштаба. Ее строят с учетом следующих соображений. При масштабе плана 1:10 000
расстоянию между нитями на палетке в 2 мм соответствует 20 м на местности,
следовательно, каждому сантиметру длины полосы на плане будет в натуре
соответствовать площадь в 0,2 га. Если на прямой отложить несколько отрезков по
1 см, сделать соответствующие подписи и один отрезок разделить на мелкие
части (см. рис. 181), то достаточно к такой шкале приложить раствор
циркуля, соответствующий сумме средних линий трапеций. Прочитанный отсчет по
шкале даст площадь в гектарах.
Аналогично
этому может быть построена шкала и для другого масштаба. Так, для масштаба 1 :
25 000 целесообразно за основание шкалы взять отрезок в 0,8 см, что будет
соответствовать 1 га.
Для
квадратной палетки пример:
Палетка
2х2мм,
Масштаб
плана 1:1000 – в 1мм – 1м, значит:
1квадрат
= 2м * 2м = 4м2,
Если
занято контуром 60 квадратов, то 60 *4 м2 = 240 м2
1.4.
Механический метод.
Механический
способ заключается в измерении площадей плоских произвольных фигур на плане
(карте) с помощью специальных приборов — планиметров,
относящихся к семейству механико-математических интеграторов. Они бывают самых
разнообразных систем: от очень простых до очень сложных. Примером простейшего
планиметра может служить планиметр А. Амслера (1854г.). В это же время нашим
соотечественником Зарубиным П.А. был изобретен такой же по идее планиметр, но
более сложной конструкции. Подобные планиметры в настоящее время не применяют.
По
конструктивным
особенностям современные планиметры различают: полярные и роликовые (линейные).
К полярным относят планиметры, у которых одна точка (полюс) во
время обвода фигуры неподвижна, а к роликовым (линейным) — у
которых все точки прибора во время обвода фигуры подвижны.
По
способу фиксации результатов измерений на счетных устройствах различают механические
и электронные устройства и в связи с этим появились термины:
механические планиметры и электронные (цифровые) планиметры.
1.4.1.
Полярный планиметр.
Планиметрами
называются приборы, при помощи которых можно получать площади криволинейных и
прямолинейных фигур по плану или топографической карте механически. Наиболее
часто
пользуются
полярным, или круговым, планиметром, представляющим собой соединение двух
рычагов R и
R1
(рис. 71). Рычаг R1
называется полюсным. Он имеет на одном
конце достаточно тяжелую гирьку Г, имеющую форму цилиндра. В нижнем основании
цилиндра имеется острая иголочка (полюс), при помощи которой планиметр
закрепляется на бумаге плана (иголочка вонзается в бумагу, и вокруг нее
вращается вся система планиметра). На другом конце рычага есть отросток с
шариком, который вкладывается в соответствующее углубление в раме М со
счетным механизмом (рис. 72) и служит вертикальной осью вращения рычагов.
В
указанной раме с одной стороны в двух выступах имеются отверстия,
в которые вставляется одним концом о б водный рычаг R,
имеющий на другом конце обводный шпиль S.
Рычаг можно в раме передвигать и тем изменять его
длину. В выступах рамы с другой стороны расположен счетный механизм, состоящий
из счетного ролика (колеса) к, вращающегося в на горизонтальной оси,
параллельной обводному рычагу. Эта ось посредством бесконечного (червячного)
винта сопряжена с шестеренкой циферблата z, который разделен по окружности на
10 равных частей.
Цилиндрическая
поверхность счетного ролика разделена на 100 равных частей. На несколько
выступающем над цилиндрической поверхностью ободке счетного ролика нанесены
мелкие рубчики — рифельные штрихи, параллельные оси вращения ролика, а
следовательно, и обводному рычагу. Благодаря этому движение по бумаге обводного
рычага, опирающегося на обводный шпиль и ролик, передается вследствие силы
трения (как говорят — по принципу фрикционного сцепления) ролику. При движении
обводного рычага перпендикулярно к своей оси ролик будет только вращаться
(предполагается, что плоскость ободка ролика перпендикулярна к оси его
вращения), а при движении по направлению вдоль оси рычага ролик будет только
скользить; при движении по любому иному направлению ролик частично будет
скользить, частично вращаться. По длине дуги, на которую ролик повернется при
обводе шпилем по всему контуру, и определяют площадь контура. Длина дуги
выражается числом делений ролика. Таким образом, при работе планиметром дело
сводится к определению числа делений ролика, на которое оно повернется при
обводе контура шпилем. Для этого по ролику производятся отсчеты перед началом
движения и по его окончании. Разность этих отсчетов и выразит искомое число
делений. Отсчеты производятся: тысячи делений по индексу циферблата, сотни и
десятки — на цилиндрической поверхности ролика по нулевому штриху (индексу)
верньера и единицы — по верньеру.
Таким
образом планиметр имеет три основные части:
1.Полюсный
рычаг.
2.Обводной
рычаг.
3.Счетный
механизм, который состоит из:
a) Счетчик
оборотов счетного ролика.
b) Счетный
ролик с червяком.
c) Верньер.
1.4.2. Верньер (нониус).
Верньер,
называемый также иногда нониусом, представляет собой построение, позволяющее
более или менее точно отсчитывать доли делений, нанесенных на инструменте. На
ролике планиметра нанесены штрихи через интервалы, которые считаются за 10
делений планиметра. Чтобы увереннее отсчитывать десятые доли этих интервалов,
т. е число единичных делений, и устраивается верньер.
Верньер
строится на небольшой части поверхности такого же цилиндра, как и ролик, и плотно
прилегает к нему по линии .4-5 (рис. 73, деления изображены в увеличенном
виде), но так, чтобы при вращении ролика между ними не возникало трения. Для
построения верньера берется расстояние в 9 интервалов ролика и делится на 10
частей. Значит один интервал верньера составляет 0,9 интервала ролика, т. е.
меньше последнего на 0,1 его величины, что является одним делением планиметра.
Если нулевой штрих (индекс) верньера совместить с каким-либо штрихом ролика (т.
е. установить их так, чтобы они образовали одну прямую линяю), то первый штрих
верньера не дойдет до следующего штриха ролика на 1 деление, второй — на 2
деления и т. д. Если, наоборот, первый штрих верньера совпадает с каким-либо
штрихом ролика, то индекс верньера прошел за предыдущий штрих ролика на 1
деление: если совпадает второй штрих верньера с каким-либо штрихом ролика, то
индекс верньера прошел за предыдущий штрих ролика на 2 деления, и т. д.
Пусть
с каким-то (безразлично с каким) штрихом ролика совпал четвертый штрих
верьньера (рис. 74). Это значит, что индекс верньера прошел за предыдущий штрих
ролика на 4 деления. Цифры 4 и 5, написанные против штрихов ролика, означают
сотни его делений. Следовательно, отсчет по ролику на рисунке будет
400+10+4=414 делений. Если при этом еще было отсчитано по циферблату 3, то
общий отсчет составит 3414 делений.
Точностью
верньера называется величина (t),
которая выражает собой ту наименьшую долю делений
инструмента, которую можно отсчитать при помощи данного верньера. Для
определения точности данного верньера практически нужно сосчитать число
делений на верньере и разделить на него цену деления инструмента.
При
отсчете по верньеру следует номер совпадающего штриха его умножать на
точность. В действительности, однако, штрихи верньера подписываются
числами, выражающими произведения номеров штрихов на точность, так что
отсчеты читаются непосредственно.
Отсчет
по планиметру состоит из четырех цифр:
1. 1-я
цифра записывается со счетчика оборотов, (как меньшая по стрелке).
2. 2-я
цифра записывается со счетного ролика, (подписанная на нем ниже нуля верньера).
3. 3-я
цифра записывается со счетного ролика по количеству неподписанных делений ниже
нуля верньера.
4. 4-я
цифра представляет собой десятую часть неподписанного деления ниже нуля
верньера, берется по номеру совпадающего на верньере штриха.
1.4.3.
Цена деления планиметра, ее определение и изменение.
Обвод
контуров планиметром можно выполнять двумя способами, устанавливая полюс
планиметра вне контура или (для слишком больших контуров) внутри него.
На практике обычно применяют первый способ, предпочитая его даже и при
больших контурах, для чего последние расчленяют карандашными линиями на мелкие
части и площадь контура находят как сумму площадей таких частей.
Обозначим
отсчет по верньеру в начале обвода буквой а и в конце обвода буквой в.
Если обвод производится по ходу часовой стрелки, то последний отсчет будет
больше первого и, следовательно, число всех делений, на которое повертывается
ролик, составит в—а
Разность
отсчетов по верньеру выражает площадь контура в делениях планиметра;
Площадь,
соответствующая одному делению планиметра называется ценой деления планиметра
Цена
деления планиметра определяется в следующей последовательности:
1. Вычисляют
теоретически площадь правильной геометрической фигуры (квадрата, прямоугольника
или круга). Можно воспользоваться сеткой координат.
М 1:2 000
В
1см – 20м
Сторона
квадрата 10см с учетом масштаба 200м
Площадь
квадрата Sкв=а2 =2002=40 000м2=4га
Площадь
фигуры =4га*3кв=12га
2. Устанавливают
планиметр на план (на лист). Выбирают место полюсу так. Чтобы при обводке
фигуры угол между рычагами был в пределах 30-150о, а при установке
иглы над начальной точкой – 90о. При обводке фигуры счетному
механизму не должно быть помех.
3. Ставят
иглу на начальную точку и записывают отсчет а равный показаниям на
счетчике.
4. Обводят
фигуру по часовой стрелке не отклоняясь от ее границ и возвращаются в начальную
точку.
5. Записывают
конечный отсчет, который увеличится (в-а) (если
обводить контур по часовой стрелке) или уменьшиться (а-в) (если
обводить контур против часовой стрелки).
6. Изменив
отсчет, обводят контур еще раз и вычисляют разность отсчетов (в1-а1).
Можно не менять отсчет, а принять за начальный отсчет второй обводки конечный
отсчет первой обводки.
7. Расхождение
между результатами первой и второй обводки зависит от величины обводимой
площади, но не должно превышать 5 делений планиметра.
8. Вычисляют
цену деления планиметра:
Спл = S фигуры/
(в – а)среднее = цена деления планиметра
1.4.4.
Поверки планиметра.
Теория
полярного планиметра основана на том, что при движении обводного рычага в
направлении, перпендикулярном к плоскости ободка ролика, последний только
скользит по бумаге, не вращаясь и, следовательно, не изменяя отсчета на
верньере, а при движении обводного рычага в направлении, совпадающем или
параллельном с плоскостью ободка, он только вращается. Все это выполняется при
условии, если,
во-первых,
на движение ролика не влияют никакие другие причины, кроме трения его ободка о
бумагу плана,
во-вторых,
если плоскость ободка перпендикулярна к оси его вращения, а последняя
параллельна оси обводного рычага.
Таким
образом, к планиметру должны предъявляться следующие требования.
1.Счетное
колесо должно вращаться свободно, без трения, не иметь колебаний по оси и
близко прилегать к верньеру, но без соприкосновения с ним.
2.Плоскость
ободка ролика должна быть перпендикулярна к его оси, а последняя параллельна
оси обводного рычага.
При
вращении колеса происходит трение в концах его оси о подшипники. Поэтому, прежде
всего, следует добиться, чтобы ось не была сильно зажата в подшипниках. Это
достигается удалением подшипников от концов оси при помощи вывинчивания
регулирующих винтиков (причем не следует забывать, предварительно откреплять
зажимные винты последних). Однако чрезмерное удаление подшипников может
привести к тому, что концы оси будут колебаться в них — появятся так называемые
боковые колебания оси ролика, чего не должно быть (ось ролика во время работы
должна занимать одно определенное положение, параллельное оси обводного
рычага). Соответствующей осторожной регулировкой следует добиться, чтобы ролик
вращался совершенно свободно, но без боковых колебаний. Эта регулировка
производится на глаз и на ощупь. Удерживая рычаг в воздухе, сообщают ролику
легким ударом пальца вращательное движение. При правильной установке это
движение должно быть быстрым и довольно продолжительным.
Кроме
трения в подшипниках, возможно еще трение ролика о верньер, если плоскости не
будут соприкасаться. С другой стороны, для уверенных и более точных отсчетов по
верньеру необходимо, чтобы плоскости эти были расположены, возможно, ближе одна
от другой (чтобы совпадающие штрихи колеса и верньера казались одной
неразрывной линией). Таким образом, здесь выявляется необходимость выполнения
двух противоречащих друг другу условий. Это достигается также действием
регулирующих винтиков, причем одному из них сообщается положительное, а
другому отрицательное вращение.
Что
касается перпендикулярности плоскости ободка ролика к его оси вращения, то это
достаточно точно выполняется на заводах, где изготовляются планиметры. На
роликах планиметров, выпускаемых нашими заводами, уклонение конца радиуса
ободка от перпендикулярного к оси положения не превышает 0,01 мм. Это при
длине радиуса 10 мм дает угол 3′,4, что па обводе контура отражается незаметно.
Поверка
параллельности оси вращения колеса с осью рычага может быть произведена методом
обвода одного и того же контура при двух различных положениях рычагов
планиметра (или, как иногда выражаются, счетного механизма) относительно
линии, соединяющей полюс и конец обводного шпиля, один раз — вправо от нее
(если, например, смотреть от полюса шпиль), другой раз — влево.
Этот
метод будем называться полным приемом; обвод же при одном только положении
рычагов будет называться п о л у п р и е м о м. При обведении контура полным
приемом, с одинаковой установкой полюса относительно контура в полуприем а х,
ошибка будет иметь в полуприемах разные знаки с одинаковой абсолютной
величиной, что и скажется на результатах обвода. Если расхождение между
площадями, выраженными в делениях планиметра, в полуприемах не превышает 2—3
делений, то условие считается выполненным. В противном случае условие не
выполнено, но среднее арифметическое из обоих полуприемов даст правильную
величину площади контура: при работе полным приемом ошибки компенсируются, что
и послужило причиной названия таких планиметров компенсационными.
Если
полюс планиметра установить так, чтобы при обводе одной половины контура углы
между рычагами все время были тупые, а в другой половине — острые, то ошибка
от не параллельности оси колеса с осью рычага более или менее компенсируется и
при работе одним полуприемом.
В
планиметрах для урегулирования параллельности оси колеса с осью обводного рычага
имеется приспособление в виде исправительного винта, упирающегося концом в
одну из плоскостей обводного рычага, к противоположной плоскости которого
прилегает пружина. Регулирование обычно производится многократным повторением
поверки (методом последовательных приближений).
Заметим,
что при обводах для проверки параллельности оси колеса с осью обводного рычага
лучше использовать контрольную линеечку, которая прилагается к планиметру и
представляет собой металлическую линейку с иглой-полюсом вблизи одного конца и
с индексом на другом конце. На линейке на определенных расстояниях от иглы
расположены углубления для обводного шпиля. Воткнув иглу в бумагу и поместив в
одно из углублений шпиль, обводят полную окружность (с радиусом, равным
расстоянию от иглы до углубления), для чего в начале обвода отмечают против
индекса точку, на которой и заканчивают обвод. При таком обводе на колесе не
отражаются сотрясения руки и площадь обведенного круга в делениях получается
точнее.
1.4.5.
Правила работы планиметром.
Наиболее
благоприятные условия для обвода площади планиметром будут в случае, когда
бумага наклеена на ровную фанеру или на мензульную доску, которые располагаются
на горизонтальной поверхности стола.
Обводный
шпиль следует поместить для начала обвода в конце примерной линии симметрии А
В данного контура (рис. 75), а полюс — на перпендикуляре, восстановленном
из середины М этой линии и притом так, чтобы рычаги образовали между
собой прямой угол. Тогда при прохождении шпиля в верхней половине фигуры угол
между рычагами все время будет тупой, а при прохождении в нижней половине— все
время острый, благодаря чему ошибки будут более или менее компенсироваться.
Перед
окончательной установкой полюса следует сделать примерный быстрый обвод всего
контура, чтобы убедиться, что при обводе не образуется слишком острых и тупых
углов между рычагами планиметра и что ролик все время вращается свободно и не
сходит
с бумаги. Сам обвод должен производиться равномерно, не быстро, но и не слишком
медленно, причем глаз должен быть расположен по направлению движения шпиля
(впереди или сзади него), что необходимо для удержания острия шпиля на контуре.
В планиметрах МШ13 шпиль обводного рычага заменен стеклом, на нижней
сферической поверхности которого отмечена точка, которой и ведут по контуру,
глядя сверху. Совмещение такой точки с контуром выполняется легче и точнее.
Рукоятку
шпиля следует держать свободно, без напряжения, чтобы рычаг давил на бумагу
только своей тяжестью, потому что иначе под действием прилагаемой силы
возможно ослабление давления колеса на бумагу и даже его поднятие, т. е.
проскоки в его вращении, приводящие к грубым ошибкам в числе делений.
Для
контроля обвода и уточнения результата каждый контур должен обводиться не менее
двух раз. При этом второй обвод лучше производить в направлении,
противоположном первому, чтобы по возможности компенсировать ошибки, зависящие
от напряжений планиметра, которые при таком методе будут иметь различные знаки.
Полезно также между обводами несколько перемещать полюс планиметра на новое
место, чтобы дать возможность ролику катиться по другому пути и тем избавиться
от накопления одинаковых ошибок, зависящих от шероховатости бумаги, а также,
чтобы избежать влияния изношенности гнезда полюса.
После
двух обводов вычисляют разности отсчетов, которые не должны превышать:
При
допустимой разности берут среднее арифметическое из обоих отсчетов. В
противном случае обводы повторяют.
Если
нуль циферблата при обводе пройдет мимо индекса (указателя), то последующий
отсчет получится меньше предыдущего. В этом случае для образования разности
нужно к последующему отсчету прибавить 10 000.
Отсчеты,
разности и вычисленные площади следует аккуратно записывать в особую
ведомость, форма которой может иметь вид, приведенный в таблице 13.
Площадь
контура вычисляют по формуле:
Sконтура= Спл (в-а)ср
1.4.6.
Постоянное число планиметра.
Если
контур, площадь которого подлежит определению, большой, то полюс планиметра
можно устанавливать внутри контура. В этом случае к разности отсчетов fl прибавляется
постоянное число q,
так что формула планиметра принимает вид
Для
определения постоянного числа одну и ту же фигуру со значительной площадью
тщательно обводят планиметром как с полюсом вне фигуры, так и с полюсом внутри
нее.
Обозначим
разность отсчетов при полюсе вне фигуры через f, и при полюсе внутри нее через
f1,. Тогда
Число
q определяется
многократными обводами при разных положениях планиметра.
1.4.7.
Точность измерения площадей полярными планиметрами.
Точность
определения площадей полярными планиметрами зависит от многих причин: от
величины площади, конфигурации участка, длины обводного рычага (или величины
зависящей от него цены деления), от методов работы, качества бумаги плана и т.
д.
При
двойных обводах съемочных контуров величиной в среднем 50 см2 и
средней вытянутостью примерно 1:4, планиметром с абсолютной ценой деления
около 0,1 см2, средняя относительная ошибка получается примерно 1/400.
Большие контуры обводятся точнее, меньшие — менее точно.
Особенно
низкая точность получается при обводе малых контуров, величиной менее 10 см2.
Это происходит главным образом потому, что ошибка отсчета по верньеру, не
зависящая от величины контуров, на малых контурах отражается значительно
сильнее. Для повышения точности определения площадей малых контуров их следует
обводить методом повторений, т. е. обводить каждый контур несколько раз, причем
отсчет брать только в начале первого и в конце последнего обводов, благодаря
чему обводка отсчета уменьшается в число раз, равное количеству обводов.
Полезно также при этом устанавливать и меньшую цену деленной, т. е. увеличивать
обводный рычаг примерно в два раза. При двух обводах с двумя повторениями в каждом
обводе и при укороченном в два раза рычаге (т. е. с ценой деления около 0,05
см2) относительная ошибка малых контуров получается не грубее 1/100.
1.4.8.
Применение современной вычислительной техники для определения площадей.
Определение
площадей землепользований, земельных участков и сельскохозяйственных угодий
является одним из трудоемких видов работ в комплексе топографо-геодезических
изысканий для землеустройства и кадастра недвижимости.
Последние
десятилетия прошлого века ознаменовались тем, что в мировой и отечественной
практике наметились частичная и полная автоматизация определения площадей.
Частичная
автоматизация — применение различных видов электронных приборов: цифровых
планиметров, дигитайзеров, позволяющих автоматизировать процесс измерений и
вычислений. В этом случае обвод контуров осуществляется оператором, но нет
необходимости производить отсчеты до и после обвода, т. к. значение площади
сразу после обвода выводится на жидко-кристаллическом дисплее счетного
механизма.
Электронные
планиметры имеются двух видов: полярные компенсационные (рис. 4.17) и линейные
(роликовые) (рис. 4.18).

различные модификации электронных планиметров, например, полярные планиметры
моделей: КР-82Ы, РЬАМХ-5.6 (Япония) и др.
Планиметры
позволяют выполнять измерения в делениях планиметра; устанавливать единицы
измерений; накапливать результаты измерений нескольких контуров. Площадь,
измеренная повторно (не более 9 раз), может быть осреднена для получения более
точного результата. При обводе вкрапленных контуров против хода часовой стрелки
их площадь автоматически вычитается из площади основного контура.

отметить, что линейные планиметры типа Х-РLAN
360 d
(рис. 4.19) позволяют быстро измерять площади участков, длины линий и контуров
по планам (картам). Длины прямых линий определяются путем фиксации двух точек —
начала и конца прямой, криволинейные контуры определяются путем их
отслеживания. Имеется встроенный калькулятор, позволяющий производить различные
операции над результатами измерений. При наличии программного обеспечения можно
дополнительно определять координаты точек на плане. Режимы измерений: точечный
— измерение только поворотных точек контура при прямолинейных границах между
ними; непрерывный — измерение криволинейных контуров путем их отслеживания.
При
обводе контура обводным индексом (курсором) прибора по ходу часовой стрелки
координаты могут регистрироваться только при нажатии клавиши на поворотных
точках или по всей границе через выбранный интервал времени, например через 1
с, либо через шаг расстояния, например через 1 мм.
В
алгоритме планиметра типа Х-РLAN
360d
может быть предусмотрено уравнивание площадей с учетом деформации бумаги,
обобщения контура в пределах шага регистрации координат, погрешностей
вторичного измерения координат на линии смежных участков (контуров).
Продолжительность
непрерывной работы разных моделей от 15 до 30 часов, а продолжительность
перезарядки аккумуляторной батареи — от 8 до 15 часов.
Точность
работы электронных планиметров в % при различных значениях площади на плане
приведена в табл. 4.1.

4.1
Полная
автоматизация — автоматическое отслеживание контура, процесса измерения и
вычисления площадей, которые реализуется в различных ГИС-технологиях. В этом
случае предполагается, что оператор работает с электронным планом (картой). При
этом точность определения площади участков по плану будет зависеть оттого,
какой точностью обладала исходная геодезическая информация в базе данных. Если
она получена в результате полевых работ, то точность определения площади будет
соответствовать точности измерений на местности (аналитическому способу). Когда
база данных формировалась путем сканирования (дигитализации) планово-картографического
материала, то точность площади будет соответствовать графическому способу.



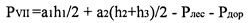
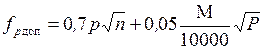
 Аналитический способ
Аналитический способ Графический метод
Графический метод









