Треугольник это геометрическая фигура (многоугольник), ограниченная со всех сторон замкнутой ломаной линией, состоящая из трех отрезков.
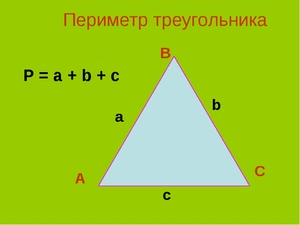
Формула периметра треугольника
Периметр треугольника равняется сумме всех его сторон: P = a + b + c,
где P это периметр и a, b, c – стороны треугольника.
Расчет периметра треугольника
Формула площади треугольника
1. Самая простая формула для расчета площади это произведение основания и высоты треугольника, поделенное на 2: S = (a · h)/2,
где S это площадь, a – основание, h – высота.
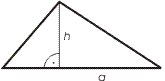
Расчет:
2. Вторая формула для расчета площади треугольника: по радиусу вписанной окружности и периметру: S = (r · P)/2 = r · p,
где r это радиус вписанной окружности, P – периметр треугольника, p – половина периметра треугольника (p = P/2)
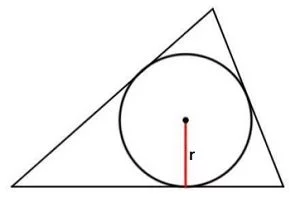
Расчет:
3. Площадь треугольника по двум сторонам и углу между ними: S = a · b · sin γ)/2 = (b · c · sin α)/2 = (a · c · sin β)/2,
где a, b, c это стороны треугольника и α, β, γ – его внутренние углы.
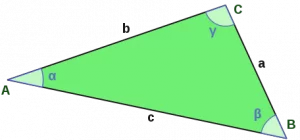
Расчет:
4. Формула Герона или площадь треугольника по его трем сторонам: S = √p · (p — a)(p — b)(p — c),
где a, b и c это стороны треугольника и p – половина периметра треугольника.
Расчет:
Что такое периметр треугольника?
Периметром треугольника называется сумма длин всех его сторон.
Как найти/вычислить периметр треугольника?
Для получения периметра треугольника нужно сложить все его стороны: P = a + b + c,
где P это периметр и a, b, c – стороны треугольника.
Чему равен периметр треугольника?
Периметр треугольника равен сумме всех его сторон.
Как найти/посчитать площадь треугольника?
Для того, чтобы вычислить площадь треугольника, можно использовать одну из формул ее вычисления, используя доступные вводные данные.
- произведение основания и высоты треугольника, поделенное на 2: S = (a · h)/2,
где S это площдаь, a – основание, h – высота. - по радиусу вписанной окружности и периметру: S = (r · P)/2 = r · p,
где r это радиус вписанной окружности, P – периметр треугольника, p – половина периметра треугольника (p = P/2) - по двум сторонам и углу между ними: S = a · b · sin γ)/2 = (b · c · sin α)/2 = (a · c · sin β)/2,
где a, b, c это стороны треугольника и α, β, γ – его внутренние углы. - по трем сторонам: S = √p · (p — a)(p — b)(p — c),
где a, b и c это стороны треугольника и p – половина периметра треугольника.
Данный сайт использует файлы куки для обеспечения наилучшей функциональности и эфективности работы. Продолжая пользоваться сайтом вы соглашаетесь с политикой использования куки. Согласен Подробнее
Периметр и площадь треугольника
- Периметр
- Площадь
Периметр
Периметр любого треугольника равен сумме длин трёх его сторон. Общая формула для нахождения периметра треугольников:
P = a + b + c,
где P — это периметр треугольника, a, b и c — его стороны.

Периметр равнобедренного треугольника можно найти сложив последовательно длины его сторон или умножив длину боковой стороны на 2 и прибавив к произведению длину основания. Общая формула для нахождения периметра равнобедренных треугольников будет выглядеть так:
P = 2a + b,
где P — это периметр равнобедренного треугольника, a — любая из боковых сторон, b — основание.

Периметр равностороннего треугольника можно найти сложив последовательно длины его сторон или умножив длину любой его стороны на 3. Общая формула для нахождения периметра равносторонних треугольников будет выглядеть так:
P = 3a,
где P — это периметр равностороннего треугольника, a — любая из его сторон.

Площадь
Для измерения площади треугольника можно сравнить его с параллелограммом. Рассмотрим треугольник ABC:

Если взять равный ему треугольник и приставить его так, чтобы получился параллелограмм, то получится параллелограмм с той же высотой и основанием, что и у данного треугольника:

В данном случае общая сторона сложенных вместе треугольников является диагональю образованного параллелограмма. Из свойства параллелограммов известно, что диагональ всегда делит параллелограмм на два равных треугольника, значит площадь каждого треугольника равна половине площади параллелограмма.
Так как площадь параллелограмма равна произведению его основания на высоту, то площадь треугольника будет равна половине этого произведения. Значит для ΔABC площадь будет равна
Теперь рассмотрим прямоугольный треугольник:

Два равных прямоугольных треугольника можно сложить в прямоугольник, если прислонить их друг к другу гипотенузой. Так как площадь прямоугольника равна произведению его смежных сторон, то площадь данного треугольника равна:
Из это можно сделать вывод, что площадь любого прямоугольного треугольника равна произведению катетов, разделённому на 2.
Из данных примеров можно сделать вывод, что площадь любого треугольника равна произведению длин основания и высоты, опущенной на основание, разделённому на 2.
Общая формула площади треугольника:
где S — это площадь треугольника, a — его основание, ha — высота, опущенная на основание a.
Периметр и площадь треугольника
Периметр
Периметр любого треугольника равен сумме длин трёх его сторон. Общая формула для нахождения периметра треугольников:
где P — это периметр треугольника, a, b и c — его стороны.

Периметр равнобедренного треугольника можно найти сложив последовательно длины его сторон или умножив длину боковой стороны на 2 и прибавив к произведению длину основания. Общая формула для нахождения периметра равнобедренных треугольников будет выглядеть так:
где P — это периметр равнобедренного треугольника, a — любая из боковых сторон, b — основание.

Периметр равностороннего треугольника можно найти сложив последовательно длины его сторон или умножив длину любой его стороны на 3. Общая формула для нахождения периметра равносторонних треугольников будет выглядеть так:
где P — это периметр равностороннего треугольника, a — любая из его сторон.

Площадь
Для измерения площади треугольника можно сравнить его с параллелограммом. Рассмотрим треугольник ABC:

Если взять равный ему треугольник и приставить его так, чтобы получился параллелограмм, то получится параллелограмм с той же высотой и основанием, что и у данного треугольника:

В данном случае общая сторона сложенных вместе треугольников является диагональю образованного параллелограмма. Из свойства параллелограммов известно, что диагональ всегда делит параллелограмм на два равных треугольника, значит площадь каждого треугольника равна половине площади параллелограмма.
Так как площадь параллелограмма равна произведению его основания на высоту, то площадь треугольника будет равна половине этого произведения. Значит для ΔABC площадь будет равна
Теперь рассмотрим прямоугольный треугольник:

Два равных прямоугольных треугольника можно сложить в прямоугольник, если прислонить их друг к другу гипотенузой. Так как площадь прямоугольника равна произведению его смежных сторон, то площадь данного треугольника равна:
Из это можно сделать вывод, что площадь любого прямоугольного треугольника равна произведению катетов, разделённому на 2.
Из данных примеров можно сделать вывод, что площадь любого треугольника равна произведению длин основания и высоты, опущенной на основание, разделённому на 2.
Общая формула площади треугольника:
где S — это площадь треугольника, a — его основание, ha — высота, опущенная на основание a.
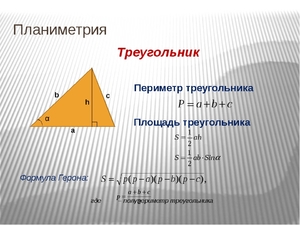
Формулы определения периметра, площади и сторон треугольника
Треугольник — это элементарная геометрическая фигура, содержащая минимально возможное количество составляющих — три.
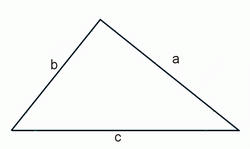
Точки соприкосновения сторон являются вершинами его углов, обозначаются заглавными латинскими символами A; B и C. Отрезки между вершинами являются сторонами или гранями треугольника и обозначаются названиями этих вершин: AB; BC; CA или прописной буквой противолежащего угла (вершины): AB=c; BC=a; CA=b.
Периметр равен длине всех сторон фигуры, у треугольника он равен сумме трех сторон:
Высота треугольника — это перпендикуляр от прямой, на которой лежит основание, до одноименной вершины, обозначается h.
Площадь составляет величину поверхности, заключенной внутри фигуры, обозначается S. Произведение основания на высоту дает значение площади. Ее можно определить и по формуле Герона:
Из этого видео вы узнаете, как найти площадь треугольника.
Классификация треугольников
Треугольник состоит из сторон и углов, сумма его углов всегда равна 180 градусов: A+B+C=180°.
- Равноугольный: все вершины равны 60°, будет и равносторонним.
- Равнобедренный: при равенстве двух граней углы на основании равны.
- Разноугольный: все вершины разные, ребра у него тоже разные.
- Прямоугольный: один угол равен 90°, примыкающие грани называются катеты, противолежащая — гипотенуза. Бывает равнобедренным (катеты равны) или разноугольным (катеты разные).
- Тупоугольный: один угол больше 90°. Может быть равнобедренным или разноугольным.
Описание
Чтобы описать любой треугольник, достаточно указать:
- Одну сторону и прилегающие к ней углы.
- Две стороны и угол между ними.
- Три стороны.
Данных из любого пункта достаточно для построения заданной фигуры и вычисления всех ее параметров, используя теорему косинусов:
Подставляя известные значения, получим уравнение, решив которое узнаем неизвестные величины.
Cos90°=0, поэтому для прямоугольного треугольника c*c=a*a+b*b, где a и b — катеты, c — гипотенуза, сторона, лежащая напротив прямого угла.
Примеры
Известно, что одна грань равна 9 см и прилегающие углы по 60 градусов. Тогда из того, что сумма углов всегда равна 180°, получаем: 180=60+60+x; x=180—120=60. Все три вершины по 60°, значит, все стороны равны. Периметр составляет P=9+9+9=27 см, полупериметр p=13,5 см. Чтобы найти высоту, нужно опустить перпендикуляр из вершины на основание, получим прямоугольный треугольник с гипотенузой 9 см, катетом 4,5 см и катетом неизвестной длины, равным искомой высоте: 9*9—4,5*4,5=60,75=h 2 .
Высота равна корню квадратному из 60,75 или 7,79422863406 см. Умножаем основание на высоту, делим пополам и получаем площадь: 7,79422863406*9/2=35,074028853 см 2 . Если находить площадь по формуле Герона через полупериметр и ребра, ответ будет одинаковый:
S=√(13,5·(13,5—9)·(13,5—9)·(13,5—9))=35,074028853 см 2 .
Следующий пример с разносторонним треугольником. Дано: AB=12 см, BC=10 см, CA=8 см. Требуется найти периметр и площадь фигуры. P=a+b+c=BC+CA+AB=10 см+8 см+12 см=30 см. Площадь находим по формуле Герона, подставляя в нее уже известные значения, учитывая, что p=0,5Р; p=15 см. S=√(p·(p—a)·(p—b)·(p—c))=√(15·(15—10)·(15—8)·(15—12))=√15·5·7·3=√1575=39,686269666 см 2 .
Рассмотрим пример, когда известны два катета прямоугольного треугольника. Допустим, они имеют значения два и четыре метра. Тогда гипотенуза будет равна корню квадратному из суммы квадратов катетов √2 2 +4 2 =4,472135955 м. Периметр 2+4+4,472135955=10,472135955. Площадь равна половине произведения катетов S=2·4=8м 2 .
Когда известны две стороны и угол между ними, остается найти только третью сторону по теореме косинусов. Пусть известные стороны составляют значения 16 и 28 метров, а угол между ними будет в 60 градусов, тогда третья сторона будет равна корню квадратному из этого выражения 16 2 +28 2 — 2·16·28·0,5, что составит значение в 24,3310501212 м. Периметр равен 16+28+24,3310501212=68,3310501212≈68,33 м. Полупериметр будет 34,165 м. Подставляя полученные значения в формулу Герона, найдем площадь S=√(34,165·(34,165—16)·(34,165—28)·(34,165—24,33))=193,982314238 м 2 .
Если известно три параметра любого треугольника — два угла и сторона или две стороны и угол между ними, то ничего особенно сложного в нахождении неизвестных параметров треугольника — периметра, площади или высоты — нет. Нужно только внимательно производить простые вычисления. Иногда можно проявить и смекалку, разбив фигуру на несколько более простых в вычислении, например, прямоугольных треугольников. В каждом конкретном случае все зависит от исходных данных. Все формулы и вычисления, приведенные выше, верны для плоских фигур; для расположенных на сферической поверхности ход вычислений будет иным.
Видео
Это видео поможет вам закрепить полученные знания.
Площадь и периметр треугольника
Треугольник это геометрическая фигура (многоугольник), ограниченная со всех сторон замкнутой ломаной линией, состоящая из трех отрезков.
Периметр
Периметр треугольника равняется сумме всех его сторон: P = a + b + c,
где P это периметр и a, b, c – стороны треугольника.
Расчет периметра
Площадь треугольника
1. Самая простая формула для расчета площади это произведение основания и высоты треугольника, поделенное на 2: S = (a · h)/2,
где S это площдаь, a – основание, h – высота.

2. Вторая формула для расчета площади: по радиусу вписанной окружности и периметру: S = (r · P)/2 = r · p,
где r это радиус вписанной окружности, P – периметр треугольника, p – половина периметра треугольника (p = P/2)

Расчет:
3. Площадь треугольника по двум сторонам и углу между ними: S = a · b · sin γ)/2 = (b · c · sin α)/2 = (a · c · sin β)/2,
где a, b, c это стороны треугольника и α, β, γ – его внутренние углы.

4. Формула Герона или площадь треугольника по его трем сторонам: S = √ p · (p — a)(p — b)(p — c) ,
где a, b и c это стороны треугольника и p – половина периметра треугольника.
[spoiler title=”источники:”]
http://liveposts.ru/articles/education-articles/matematika/formuly-opredeleniya-perimetra-ploshhadi-i-storon-treugolnika
[/spoiler]
Содержание:
- Формулы площади треугольника
- Формула периметра треугольника
Треугольник – фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков,
попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки – его сторонами.
Формулы площади треугольника
Площадь геометрической фигуры – часть поверхности, ограниченная замкнутым контуром данной фигуры.
Величина площади выражается числом заключающихся в него квадратных единиц.
1-ая формула
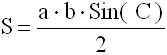
S – площадь треугольника
a, b – длины 2-х сторон треугольника
С – угол между сторонами a и b
2-ая формула
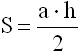
S – площадь треугольника
a – длина стороны треугольника
h – длина высоты, опущенной на сторону a
3-ья формула
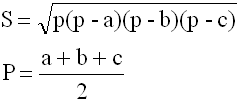
S – площадь треугольника
a, b, c – длины 3-х сторон треугольника
p – полупериметр треугольника
4-ая формула
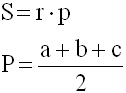
S – площадь треугольника
r – радиус вписанной окружности
p – полупериметр треугольника
5-ая формула
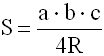
S – площадь треугольника
a, b, c – длины 3-х сторон треугольника
R – радиус описанной окружности
См. также: Программа для расчета площади треугольника.
Формула периметра треугольника
Периметр геометрической фигуры – суммарная длина границ плоской геометрической фигуры.
Периметр имеет ту же размерность величин, что и длина.
1) Периметр треугольника равен сумме 3-ех его сторон (a, b, c).
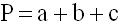
P – периметр треугольника
a, b, c – длины сторон треугольника
См. также: Программа для расчета периметра треугольника.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
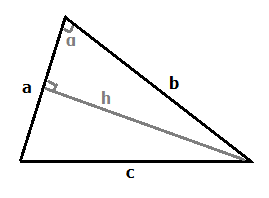
Треугольник – это многоугольник, у которого три вершины и три стороны.
Виды треугольников:
- прямоугольные треугольники;
- равнобедренные треугольники;
- равносторонние треугольники.
Любой треугольник характеризуется сторонами a, b, c и углами между ними (см. рисунок). При решении задач может понадобиться угол α между двумя из сторон треугольника, высота h, опущенная к одной из сторон, радиусы вписанной (r) и описанной (R) окружности. Именно эти характеристики используются в формулах треугольника при вычислении площади и периметра.
Формула периметра треугольника
Периметр P треугольника можно получить, зная его стороны:
P = a + b + c
При вычислении площади треугольника часто требуется знать его полупериметр:
p = P/2 = (a + b + c)/2
Формулы площади треугольника
Площадь треугольника S можно вычислить, зная его сторону a и высоту h, опущенную на эту сторону:
S = 1/2 ⋅ a ⋅ h
Площадь треугольника S также можно вычислить, зная две его стороны a и b и угол α между ними:
S = 1/2 ⋅ a ⋅ b ⋅ sinα
Еще одна формула позволяет вычислить площадь треугольника по его сторонам a, b и c и полупериметру p (формула Герона):
S = √p ⋅ (p – a) ⋅ (p – b) ⋅ (p – c)
Если в задаче присутствует окружность, вписанная в треугольник, площадь треугольника можно вычислить через его полупериметр p и радиус r:
S = r ⋅ p
Если в задаче присутствует окружность, описанная вокруг треугольника, площадь треугольника можно вычислить через его стороны a, b и c и радиус R:
S = (a ⋅ b ⋅ c)/(4R)
