как найти площадь квадрата зная периметр
АЛЕКСАНДР ЛОПАРЕВ
Знаток
(308),
закрыт
12 лет назад
Армен Арстамян
Ученик
(102)
1 год назад
Например Р=16м, нужно узнать S, да?
Так вот, у квадрата 4 стороны, соответственно Р(20м) делим на 4
(стороны) и это равняется а(5м)
Ну Sкв.= а×а
Сторону а(5м) мы знаем, теперь умножаем а(5м) на а(5м) и это будет наш S(25м²)!
Легко и просто!
Формула:
А(кв.) = P(кв.)÷4;
S(кв.) = а×а
И всё!
И чего тут сложного?…..
Введите данные:
Достаточно ввести только одно значение, остальное калькулятор посчитает сам.
Cторона квадрата, диаметр вписанной окружности (L)
Диагональ квадрата, диаметр описанной окружности (M)
Радиус вписанной окружности (R1)
Радиус описанной окружности (R2)
Округление:
* – обязательно заполнить
Периметр (P) = 10
Cторона, диаметр вписанной окружности (L) = (frac{P}{4}) = (frac{10}{4}) = 2.5
Диагональ, диаметр описанной окружности (M) = (sqrt{2*L^{2}}) = (sqrt{2*2.5^{2}}) = 3.54
Радиус вписанной окружности (R1) = (frac{L}{2}) = (frac{2.5}{2}) = 1.25
Радиус описанной окружности (R2) = (frac{M}{2}) = (frac{3.54}{2}) = 1.77
Площадь (S) = (L^{2}) = (2.5^{2}) = 6.25

{S = a ^2}
На этой странице вы найдете удобный калькулятор для расчета площади квадрата и формулы, которые помогут найти площадь квадрата через его сторону, диагональ, периметр, а также радиусы вписанной и описанной окружности.
Квадрат – четырёхугольник, у которого все углы прямые (90 градусов) и все стороны равны между собой. Из-за своих свойств квадрат часто называют правильным четырехугольником.
Содержание:
- калькулятор площади квадрата
- формула площади квадрата через сторону
- формула площади квадрата через диагональ
- формула площади квадрата через радиус вписанной окружности
- формула площади квадрата через радиус описанной окружности
- формула площади квадрата через периметр
- примеры задач
Формула площади квадрата через сторону

S = a ^2
a – сторона квадрата
Формула площади квадрата через диагональ

S=dfrac{d^2}{2}
d – диагональ квадрата
Формула площади квадрата через радиус вписанной окружности

S = 4r^2
r – радиус вписанной окружности
Формула площади квадрата через радиус описанной окружности

S = 2R^2
R – радиус описанной окружности
Формула площади квадрата через периметр

S = dfrac{P^2}{16}
P – периметр квадрата
Примеры задач на нахождение площади квадрата
Задача 1
Найдите площадь квадрата если его диагональ равна 1.
Решение
Для решения задачи воспользуемся формулой.
S = dfrac{d^2}{2} = dfrac{1^2}{2} = dfrac{1}{2} = 0.5 : см^2
Ответ: 0.5 см²
Проверим ответ на калькуляторе .
Задача 2
Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Решение
Для решения этой задачи используем формулу площади квадрата через радиус описанной окружности.
S = 2R^2 = 2 cdot 83^2 = 2 cdot 6889 = 13778 : см^2
Ответ: 13778 см²
Проверим ответ с помощью калькулятора .
Задача 3
Найдите площадь квадрата если его сторона равна 8 см.
Решение
Используем первую формулу.
S = a ^2 = 8 ^2 = 64 : см^2
Ответ: 64 см²
Проверим результат на калькуляторе .
Задача 4
Найдите площадь квадрата периметр которого равен 456 см.
Решение
Используем формулу для площади квадрата через периметр.
S = dfrac{P^2}{16} = dfrac{456^2}{16} = dfrac{456 cdot cancel{456}^{ : 57}}{cancel{16}^{ : 2}} = dfrac{57 cdot cancel{456}^{ : 228}}{cancel{2}^{ : 1}} = 57 cdot 228 = 12996 : см^2
Ответ: 12996 см²
Проверка .
Задача 5
Найдите площадь квадрата со стороной 15 см.
Решение
Воспользуемся формулой площади квадрата через сторону.
S = a ^2 = 15 ^2 = 225 : см^2
Ответ: 225 см²
Проверка .
Как находить площадь квадрата
Найти площадь такой фигуры, как квадрат, можно даже пятью способами : по стороне, периметру, диагонали, радиусам вписанной и описанной окружности.
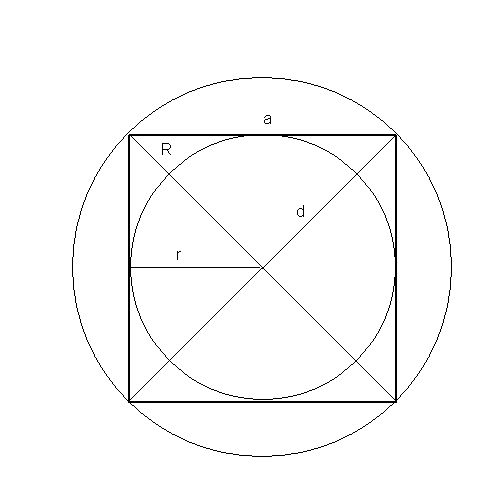
Инструкция
Если известна длина стороны квадрата, то его площадь равна квадрату (второй степени) стороны.
Пример 1.
Пусть имеется квадрат со стороной 11 мм.
Определите его площадь.
Решение.
Обозначим через:
а – длину стороны квадрата,
S – площадь квадрата.
Тогда:
S=а*а=а²=11²=121 мм²
Ответ: Площадь квадрата со стороной 11 мм – 121 мм².
Если известен периметр квадрата, то его площадь равна шестнадцатой части квадрата (второй степени) периметра.
Следует из того, что все (четыре) стороны квадрата имеют одинаковую длину.
Пример 2.
Пусть имеется квадрат с периметром 12 мм.
Определите его площадь.
Решение.
Обозначим через:
Р – периметр квадрата,
S – площадь квадрата.
Тогда:
S=(Р/4)²=Р²/4²=Р²/16=12²/16=144/16=9 мм²
Ответ: Площадь квадрата с периметром 12 мм – 9 мм².
Если известен радиус вписанной в квадрат окружности, то его площадь равна учетверенному (умноженному на 4) квадрату (второй степени) радиуса.
Следует из того, что радиус вписанной окружности равен половине длины стороны квадрата.
Пример 3.
Пусть имеется квадрат с радиусом вписанной окружности 12 мм.
Определите его площадь.
Решение.
Обозначим через:
r – радиус вписанной окружности,
S – площадь квадрата,
а – длину стороны квадрата.
Тогда:
S=а²=(2*r)=4*r²=4*12²=4*144=576 мм²
Ответ: Площадь квадрата с радиусом вписанной окружности 12 мм – 576 мм².
Если известен радиус описанной вокруг квадрата окружности, то его площадь равна удвоенному (умноженному на 2) квадрату (второй степени) радиуса.
Следует из того, что радиус описанной окружности равен половине диаметра квадрата.
Пример 4.
Пусть имеется квадрат с радиусом описанной окружности 12 мм.
Определите его площадь.
Решение.
Обозначим через:
R – радиус описанной окружности,
S – площадь квадрата,
а – длину стороны квадрата,
d – диагональ квадрата
Тогда:
S=а²=d²/2=(2R²)/2=2R²=2*12²=2*144=288 мм²
Ответ: Площадь квадрата с радиусом описанной окружности 12 мм – 288 мм².
Если известна диагональ квадрата, то его площадь равна половине квадрата (второй степени) длины диагонали.
Следует из теоремы Пифагора.
Пример 5.
Пусть имеется квадрат с диагональю длиной 12 мм.
Определите его площадь.
Решение.
Обозначим через:
S – площадь квадрата,
d – диагональ квадрата,
а – длину стороны квадрата.
Тогда, так как по теореме Пифагора: а²+а²=d²
S=а²=d²/2=12²/2=144/2=72 мм²
Ответ: Площадь квадрата с диагональю 12 мм – 72 мм².
Видео по теме
Обратите внимание
Обозначим сторону квадрата как “b”. По определению площадь – это произведение длины и ширины. Длина квадрата равняется b, ширина тоже. Следовательно, площадь квадрата можно приравнять к квадрату его стороны: S=b2.
Полезный совет
Площадь квадрата равна квадрату его стороны.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Калькулятор позволяет найти площадь квадрата по периметру.
Введите данные:
Достаточно ввести только одно значение, остальное калькулятор посчитает сам.
Cторона квадрата, диаметр вписанной окружности (L)
Диагональ квадрата, диаметр описанной окружности (M)
Радиус вписанной окружности (R1)
Радиус описанной окружности (R2)
Округление:
* – обязательно заполнить
Площадь (S) = 10
Cторона, диаметр вписанной окружности (L) = (sqrt{S}) = (sqrt{10}) = 3.16
Диагональ, диаметр описанной окружности (M) = (sqrt{2*L^{2}}) = (sqrt{2*3.16^{2}}) = 4.47
Радиус вписанной окружности (R1) = (frac{L}{2}) = (frac{3.16}{2}) = 1.58
Радиус описанной окружности (R2) = (frac{M}{2}) = (frac{4.47}{2}) = 2.24
Периметр (P) = (L*4) = (3.16*4) = 12.64
