Решение
Выразим к. п. д. электростанции через
полезную Pполи затраченнуюPзатр
мощности

Мощность Pзатрнаходится как энергия, выделяемая за 1
с при распадеNядер
урана, содержащихся в заданной массе,
Рзатр=
E0N/t.
(2)
Число ядер N равно
числу молей ν=
m/M,
умноженному на постоянную АвогадроNA(см. (27Ф))

где M–молярная
масса урана235U. С
учетом (2), (3) к. п. д. (1) равен
откуда искомая
полезная мощность
Таблица вариантов к контрольной работе
№4
Таблица содержит варианты для
специальностей, учебными планами которых
предусмотрено четыре контрольных работы
|
Вариант |
Номера задач |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
0 |
401 |
411 |
421 |
431 |
441 |
451 |
|
1 |
402 |
412 |
422 |
432 |
442 |
452 |
|
2 |
403 |
413 |
423 |
433 |
443 |
453 |
|
3 |
404 |
414 |
424 |
434 |
444 |
454 |
|
4 |
405 |
415 |
425 |
435 |
445 |
455 |
|
5 |
406 |
416 |
426 |
436 |
446 |
456 |
|
6 |
407 |
417 |
427 |
437 |
447 |
457 |
|
7 |
408 |
418 |
428 |
438 |
448 |
458 |
|
8 |
409 |
419 |
429 |
439 |
449 |
459 |
|
9 |
410 |
420 |
430 |
440 |
450 |
460 |
Задачи для самостоятельного решения
401. Определить
поток энергии, излучаемой
Солнцем, считая его абсолютно черным
телом. Температура поверхности Солнца Т=5800
К, его радиусrс=6,95.108м.
402. Найти плотность
потока солнечного излучения вблизи
поверхности Земли (за пределами ее
атмосферы), принимая Солнце за абсолютно
черное тело с температуройповерхности
Т
=
5800 К. Радиус
Солнца rc
=
6,95.108
м, радиус земной орбиты r
=
1,5.1011
м.
403. Энергетическая светимость
абсолютно черного тела
R*
=
3,0 Вт/см2.
Найти
длину волны,
соответствующую максимуму испускательной
способности этого тела.
404. В
электрической лампочке мощностьюР=25 Вт температура
спиралиТ=2450 К. Отношение энергетической светимости
спирали к энергетической светимости
абсолютно черного тела при данной
температуреk =0,30. Найти площадь излучающей поверхности
спирали.
405. Тело нагрели до
температурыТ=2900 К. Мощность излучения с единицы
поверхности телаR=200 Вт/см2. Найти отношение
энергетической светимости этого тела
к энергетической светимости абсолютно
черного тела.
406. Найти
температуру тела,
если с площади его поверхностиS=6,0 см2излучается поток энергии Ф=34 кВт. Тело считать абсолютно черным.
407.
Абсолютно черное
тело находится при температуре
Т1
=
2900 К. В результате его охлаждения длина
волны, на которую приходится максимум
испускательной способности, изменилась
на
=
9,0 мкм. До какой температуры Т2
охладилось тело?
408. Максимум
испускательной способности Солнца
приходится на длину волны m
=
0,48
мкм. Найти массу, теряемую Солнцем за 1
с в результате излучения. Считать Солнце
абсолютно черным телом. Радиус Солнца
rс
=
6,95.108
м.
409. Поток, излучаемый
абсолютно черным телом, Ф=100 кВт. Найти площадь излучающей
поверхности, если максимум испускательной
способности приходится на длину волныm=0,60 мкм.
410. Медный шарик диаметра d
=
1,2 см поместили в откачанный сосуд,
температура стенок которого поддерживается
близкой к абсолютному нулю. Начальная
температура шарика Т0
= 300
К. Считая поверхность шарика абсолютно
черной, найти, через сколько времени
его температура уменьшится в
=
2,0 раза.
411. На поверхность металла
падает свет с длиной волны
λ =
0,36 мкм и мощностью Р
=
6,0 мкВт. Найти
фототок насыщения,
если
=
5,0% падающих фотонов выбивает из металла
электроны.
412. Найти красную границу фотоэффекта
для цинка и максимальную скорость
фотоэлектронов, вырываемых с его
поверхности
электромагнитным
излучением с длиной волны λ =250 нм.
413. При поочередном освещении поверхности
металла светом с длинами волн λ1=0,35 мкм и λ2=0,54 мкм было
обнаружено, что соответствующие
максимальные скорости фотоэлектронов
отличаются друг от друга в η=2,0 раза. Найти работу выхода с поверхности
этого металла.
414. До какого максимального потенциала
зарядится удаленный от других тел медный
шарик при облучении его электромагнитным
излучением с длиной волны λ =140 нм?
415. Найти частоту света, вырывающего с
поверхности металла электроны, которые
полностью задерживаются напряжением
Uз=3,0 В. Красная граница фотоэффекта ν0=6,0.1014Гц. Найти работу выхода электронов из
этого металла.
416. Фотоны с энергией Еф=4,9 эВ вырывают электроны из металла с
работой выходаА=4,5 эВ. Найти максимальный импульс,
передаваемый поверхности металла, при
вылете каждого электрона.
417. Фотокатод освещается излучением
длиной волны =83.нм.
Красная граница фотоэффекта0
=333 нм. На какое
максимальное расстояние от поверхности
катода может удалиться фотоэлектрон,
если вне электрода имеется однородное
задерживающее электрическое поле
напряженностьюЕ=750 В/м?
418. При увеличении частоты падающего
на металл света в два раза задерживающее
напряжение увеличивается в три раза.
Частота первоначально падающего света=1,21015Гц.
Определить красную границу фотоэффекта
для данного металла.
419. На фотокатод с работой выхода А1
=6,3 эВ падает
излучение. Для прекращения фототока
необходимо приложить задерживающее
напряжениеU1=3,7 В. Если фотокатод заменить другим, то
задерживающее напряжениеU2=6,0 В.
Определить работу выхода электронов
из второго фотокатода.
420. В сферическом сосуде, из которого
откачен воздух, помещены два электрода
из цинка (рис. 17). К ним подсоединен
конден-
сатор емкостью С=3,5 мкФ. Один из электродов освещается
светом с длиной волны λ=0,25 мкм. Какой заряд будет находиться на
конденсаторе при длительном освещении
электрода?
421. Фотон с энергией =1,0 МэВ рассеялся
на свободном покоившемся электроне.
Найти кинетическую энергию электрона
отдачи, если в результате рассеяния
длина волны фотона изменилась на η=25 %.
422. Фотон с длиной волны =6,0 пм рассеялся под прямым углом на
покоившемся свободном электроне. Найти
частоту рассеянного фотона и кинетическую
энергию электрона отдачи.
423. Фотон с импульсом Р=1,02 МэВ/с, гдес–скорость света, рассеялся на покоившемся
свободном электроне, в результате
импульс фотонаРʹ=0,255 МэВ/с. Под
каким углом рассеялся фотон?
424. Фотон рассеялся под углом θ =120она покоившемся свободном
электроне, в результате чего электрон
получил кинетическую энергиюЕк=0,45 МэВ. Найти
энергию фотона до рассеяния.
425. Найти длину волны комптоновского
излучения, если максимальная кинетическая
энергия электронов Емакс=0,19 МэВ.
426. На рис. 18 показаны несколько
энергетических уровней электронной
оболочки атома и указаны частоты фотонов,
испускаемых и поглощаемых при переходах
между этими уровнями. Найти длину волны
фотона, при поглощении которого атом
переходит с уровня Е1на уровеньЕ4. Частоты фотонов, показанных
на рисунке, ν13=6.1014Гц, ν24=4.1014Гц, ν32
=3.1014Гц.
427. В
однозарядном ионе лития электрон перешел
с четвертого энергетического
уровня на второй. Определить длину волны
λ
излучения, испущенного
ионом лития.
428. Фотон
выбивает из атома водорода, находящегося
в основном состоянии, электрон
с кинетической энергией Ек
=
10 эВ. Определить энергию ε фотона.
429. Вычислить энергию фотона, испускаемого
при переходе электрона в атоме водорода
с третьего энергетического уровня на
первый.
430. Фотон с энергией Е=16,5 эВ выбил электрон из невозбужденного
атома водорода. Какую скорость будет
иметь электрон вдали от ядра атома?
431. Атом водорода в основном состоянии
поглотил фотон с длиной волны =0,12 мкм. Определить
радиус электронной орбиты возбужденного
атома водорода.
432. Найти длину волны, соответствующую
третьей спектральной линии в серии
Бальмера.
433. Найти наибольшую и наименьшую длины
волн в первой инфракрасной серии спектра
водорода (серии Пашена).
434. Определить наибольшее и наименьшее
значения энергии фотона в ультрафиолетовой
серии спектра водорода.
435. Найти наименьшую и
наибольшую длины волн спектральных
линий водорода в видимой области спектра
(серия Бальмера).
436. Найти отношение минимальной
энергии фотона в серии Лаймана к
максимальной энергии фотона в серии
Бальмера.
437. Покоившийся атом водорода
испустил фотон, соответствующий первой
линии ультрафиолетовой серии (серии
Лаймана). Какую скорость приобрел атом?
438. Покоящийся ион гелия Не+
испустил фотон, соответствующий
первой линии серии Лаймана. Этот фотон
выбил фотоэлектрон из покоящегося атома
водорода, который находился в основном
состоянии. Найти скорость фотоэлектрона.
439. Найти длину волны де
Бройля для электрона, движущегося со
скоростью: а)
v1=
1,0 Мм/с; б)
v2
=
200 Мм/с.
440. Найти длину волны де
Бройля для электрона, имеющего кинетическую
энергию: а)
Е1
=
10 эВ; б)
Е2
= 3,0
МэВ.
441. Найти длину волны де
Бройля для электронов, прошедших разность
потенциалов U1
=
1,0 В и U2
=
1,0 МВ.
442. Заряженная частица,
ускоренная разностью потенциалов
U
=
200 В, имеет длину волны де Бройля
=
2,02 пм. Найти массу m
частицы, если ее заряд численно равен
заряду электрона.
443. С какой скоростью движется
электрон, если дебройлевская длина
волны электрона равна его комптоновской
длине волны?
444. При каком значении
кинетической энергии Ек
дебройлевская длина волны электрона
равна его комптоновской длине волны?
445. Предполагая, что
неопределенность координаты движущейся
частицы равна ее дебройлевской
длине волны, найти относительную
погрешность р/р
импульса этой частицы.
446. Электрон с кинетической
энергией Ек
=
15 эВ находится в
металлической
пылинке
диаметром d
=
1,0 мкм. Найти относительную погрешность
v/v,
c
которой можно
определить скорость электрона.
447. Найти относительное
уширение спектральной линии /,
если время жизни атома
в возбужденном состоянии
=
10–8
с,
и длина волны излучаемого фотона
=
0,60 мкм.
448. Используя соотношение
неопределенностей Е.t
ћ,
оценить уширение энергетического уровня
в атоме водорода, находящегося: а)
в основном состоянии; б)
в возбужденном состоянии. Время жизни
атома в возбужденном состоянии
=
10–8
с.
449.
Частица находится в бесконечно глубокой,
одномерной, прямоугольной
потенциальной яме. Найти отношение
разности энергий ΔEn
соседних энергетических уровней к
энергии Еп
частицы в случаях: 1)
n
=
2; 2) n
=
4; 3) n
=
7; 4) n→∞,
где n
–
главное квантовое
число. Сделать выводы.
450. Электрон находится в одномерной
прямоугольной с бесконечно высокими
стенками потенциальной яме. Найти ширину
lпотенциальной ямы,
если разность энергий между уровнями
с квантовыми числамиn1
=2 иn2
=3 составляет
∆E =0,30 эВ.
451. Частица находится в основном состоянии
в одномерной прямоугольной потенциальной
яме шириной lс
бесконечно высокими стенками. Найти
вероятность нахождения частицы в области l/3 <x
< 2l/3.
452. Найти удельную энергию связи ядер
изотопов кислорода

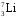
453. Какая доля радиоактивных ядер
кобальта, период полураспада которых
Т=71,3 сут,
распадется за месяц?
454. Уран 238Uмассойm=1,00 г излучаетN=1,24.104альфа-частиц в секунду.
Найти его период полураспада.
455. Активность некоторого радиоизотопа
уменьшается в n=2,5 раза за времяt=7,0 сут. Найти его период полураспада.
456. В начальный момент активность
некоторого радиоизотопа а=10,8 Бк. Какова будет его активность по
истечении половины периода полураспада?
457. Определить возраст древних деревянных
предметов, если удельная активность
(активность единицы массы вещества)
изотопа углерода 14С у них составляет
η=0,6 удельной
активности этого же изотопа в только
что срубленных деревьях. Период
полураспада этого изотопаТ=5570 лет.
458. Найти удельные активности (активность
единицы массы вещества) изотопов натрия
24Naи урана235U,
периоды полураспада которых соответственно
равныТ1=15 ч иТ2=7,1.108лет.
459. Определить скорости продуктов реакции
10B(n,
α)7Li, протекающей
в результате взаимодействия медленных
нейтронов с покоящимися ядрами бора.
460. Мощность атомной электростанции Р=5,0105кВт и к. п. д.=0,20. Определить расход урана235Uв течениеt=1,0 год и сравнить с годовым расходом
каменного угля на тепловой электростанции
той же мощности при таком же к. п. д.
461. Найти энергетический выход (энергию)
следующих реакций: а)9Ве (α,
γ)10Ве;б)7Li( α,n)10В. Использовать
табличные значения масс атомов легких
изотопов (а. е. м.)
462. Определить к. п. д. двигателя атомного
ледокола, если его мощность Р =32 Мвт и в атомном реакторе расходуется
за время t=1,0 сут уран235Uмассойm=200 г. При
делении одного ядра урана выделяется
энергияЕ0=200 МэВ.
463. В кровь человека ввели небольшое
количество раствора, содержащего
радиоизотоп натрия 24Naс активностьюа=2,0.103Бк. Активность 1 см3крови черезt=5,0 ч оказаласьаʹ=0,267 Бк/см3.
Период полураспада данного радиоизотопаТ=15 ч. Найти
объем крови человека.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Найти площадь S излучающей поверхности нити
|
Условие задачи Найти площадь S излучающей поверхности нити 25-ваттной лампы, если температура нити Т = 2450 К. Излучение нити составляет р = 30% излучения абсолютно чёрного тела при данной температуре. Потерями тепла, связанными с теплопроводностью, пренебречь. Решение задачи |
Категория: Задачи | Добавил: Creator (23.07.2016) |
| Просмотров: 5338 | Теги: температура, Абсолютно, поверхность, нить, площадь, тело, Черное, теплопроводность, лампа | Рейтинг: 0.0/0 |
Тема: Вольфрамовая спираль (Прочитано 4888 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Вольфрамовая спираль в Р = 100-ваттной электрической лампочке имеет температуру Т = 2500 К. Отношение ее энергети ческой светимости к энергетической светимости абсолютно черного тела при данной температуре k = 0,4. Найдите площадь S излучающей поверхности спирали, в предположении, что вся мощность лампочки тратится на излучение. Сделать рисунок.
« Последнее редактирование: 05 Апреля 2015, 15:10 от Сергей »
Записан
Решение.
Энергия, излучаемая с единицы поверхности абсолютно черного тела определяется формулой Стефана-Больцмана:
R = σ∙Т4 (1).
σ = 5,67∙10-8 Вт/м2∙К4.
Определим энергетическую светимость вольфрамовой лампочки:
[ frac{{{R}_{B}}}{R}=k, {{R}_{B}}=kcdot R, {{R}_{B}}=kcdot sigma cdot {{T}^{4}} (2). ]
Мощность излучения и площадь поверхности тела связаны соотношением:
[ P={{R}_{B}}cdot S (3), S=frac{P}{{{R}_{B}}}, S=frac{P}{kcdot sigma cdot {{T}^{4}}} (3). ]
S = 1,14∙10-4 м2.
« Последнее редактирование: 26 Апреля 2015, 06:31 от alsak »
Записан






Чтобы получить решение, напишите мне в WhatsApp, оплатите, и я Вам вышлю файлы.
Кстати, если эта работа не по вашей теме или не по вашим данным, не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу, я смогу выполнить её в срок 1-3 дня!
Описание и исходные данные задания, 50% решения + фотография:
№1 5. Температура вольфрамовой спирали в 40-ватной лампочки 2300 K. Отношение её энергетической светимости АЧТ при данной температуре 0,3. Найти площадь излучающей поверхности спирали.
Решение.
Энергетическая светимость абсолютно чёрного тела определяется только его температурой (закон Стефана-Больцмана): , где Вт/(м ∙К ) – постоянная Стефана-Больцмана. Энергетическая светимость есть мощность излучения с единицы поверхности тела. Мощность излучения с поверхности спирали площадью : ,
- Температура вольфрамовой спирали в электрической лампочке мощностью N = 25 Вт равна T = 2450 К. Отношение её энергетической светимости к энергетической светимости абсолютно чёрного тела при данной температуре равно 0,3. Найти величину излучающей поверхности спирали.
- Сколько энергии излучается в пространство за 10 ч с площади S = 1 га пахотной земли, имеющей температуру t = 27 °C? Считать почву чёрным телом.
- Определите относительное увеличение ∆R*/R* энергетической светимости чёрного тела при увеличении его температуры на 1 %. Условие 2 5.66. На сколько процентов увеличится энергетическая светимость абсолютно чёрного тела, если его температура T увеличится 1 %? Условие 3 53. На сколько процентов увеличится энергетическая светимость абсолютно чёрного тела, если его температура увеличится на 1 %?
- Вследствие изменения температуры чёрного тела максимум спектральной плотности (r л,T)max сместился с л1 = 0,8 мкм на л2 = 2,4 мкм. Во сколько раз уменьшилась максимальная спектральная плотность энергетической светимости?
Примеры решения задач по квантовой физике
1. Мощность излучения
абсолютно черного тела кВт. Найти площадь
излучающей поверхности тела, если максимум
спектральной плотности его энергетической светимости приходится на длину волны нм.
|
Дано: |
Решение: |
|
ачт
|
Энергетическая светимость тела по определению: или для тела равномерно излучающего со всей поверхности
где Энергетическая светимость абсолютно черного тела согласно где Согласно закону смещения где Тогда температуру тела можно
Следовательно, площадь
|
|
Ответ: |
|
2. Увеличение температуры
равновесного излучения на К привело к изменению
наиболее вероятной длины волны в его спектре на нм.
Какова начальная температура равновесного излучения?
|
Дано: |
Решение: |
|
|
Согласно закону смещения где Так как температура
Так как
Решим уравнение:
Т.к. температура
|
|
Ответ: |
|
3. Медный шарик радиусом мм с абсолютно черной поверхностью
поместили в откачанный сосуд, температура стенок которого поддерживается
близкой к абсолютному нулю К. Начальная температура
шарика К. Через какое время
его температура
уменьшится
в раза? Удельная теплоемкость меди
Дж/(кг∙К).
|
Дано: |
Решение: |
|
Шарик − ачт:
стенки сосуда: |
Энергетическая светимость тела по определению: или для шарика равномерно излучающего со всей поверхности
Энергетическая светимость абсолютно черного тела согласно где Тогда энергия, излучаемая с поверхности шарика за время
Т.к. шарик помещен в откачанный
знак «-» учитывает, что
Проинтегрируем последнее выражение:
Получим
|
|
Ответ: |
|
4. Какую мощность нужно
подводить к зачерненному металлическому шарику диаметром см, чтобы поддерживать его температуру на
К выше температуры окружающей среды?
Температура окружающей среды К. Считать, что тепло
теряется только вследствие излучения.
|
Дано: |
Решение: |
|
Шарик − ачт:
|
Энергетическая светимость тела по определению: или для шарика равномерно излучающего со всей поверхности
где Энергетическая светимость абсолютно черного тела согласно где Так как шарик можно Мощность излучения с поверхности шарика (энергия,
Так как шарик находится в среде с температурой
Чтобы поддерживать температуру шарика постоянной и
|
|
Ответ: |
|
5. Определить, с какой
скоростью должен двигаться и какую кинетическую
энергию должен иметь электрон, чтобы его импульс
был равен импульсу фотона, длина волны которого пм.
|
Дано: |
Решение: |
|
|
Импульс фотона: Импульс электрона: 1) Так как
Решим квадратное уравнение:
Кинетическая энергия электронов
2) Так как
|
|
Ответ: |
|
6. Рубиновый лазер
излучает в импульсе длительностью мс энергию
Дж в виде узкого, почти параллельного пучка
монохроматического света. Найти среднее за время импульса давление пучка света, если его сфокусировать в
пятнышко диаметром мкм на поверхность,
перпендикулярную пучку, с коэффициентом отражения .
|
Дано: |
Решение: |
|
|
Давление света:
где
|
|
Ответ: |
|
7. Определить напряжение на
рентгеновской трубке и скорость электронов ,
подлетающих к аноду рентгеновской трубки, если длина волны коротковолновой
границы сплошного рентгеновского спектра нм.
|
Дано: |
Решение: |
|
Тормозное рентгеновское излучение
|
Кинетическая энергия электронов
Максимальная энергия фотона,
Следовательно, напряжение
кинетическая энергия электронов |

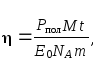
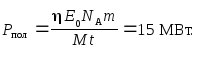







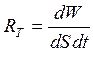
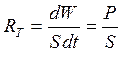 ,
,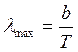 ;
;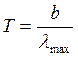 ;
; 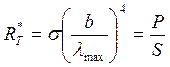 .
. м.
м.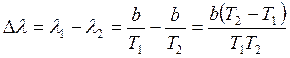 .
.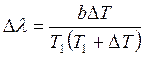 .
.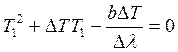 ;
; ;
; ;
;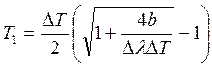 .
.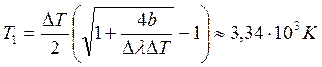 .
.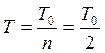
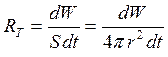 ,
,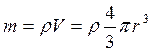 −
−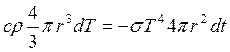 ;
;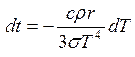 .
.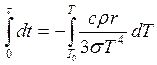 ;
;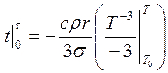 ;
;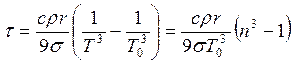 .
.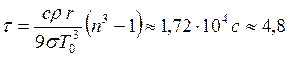 ч.
ч.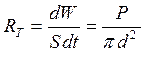 ,
,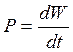 − мощность излучения,
− мощность излучения,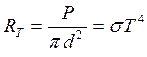 .
.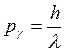 .
.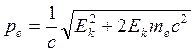 или
или 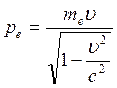 .
.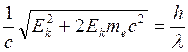 ;
;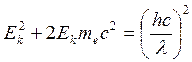 .
.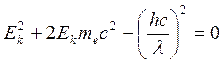 ;
;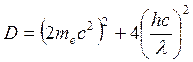 ;
;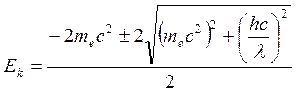 .
.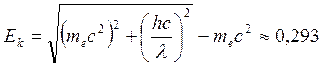 МэВ
МэВ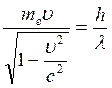 ;
;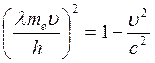 ;
;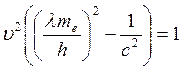 ;
;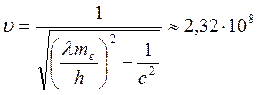 м/с.
м/с.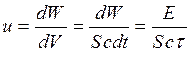 − объемная плотность
− объемная плотность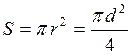 − площадь светового пятна;
− площадь светового пятна; 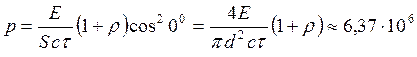 Па.
Па.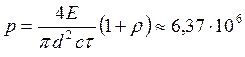 Па.
Па.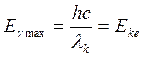 ;
;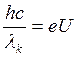 .
.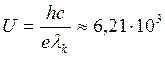 В;
В;