Примеры решения задач по квантовой физике
1. Мощность излучения
абсолютно черного тела ![]() кВт. Найти площадь
кВт. Найти площадь ![]() излучающей поверхности тела, если максимум
излучающей поверхности тела, если максимум
спектральной плотности его энергетической светимости приходится на длину волны ![]() нм.
нм.
|
Дано: |
Решение: |
|
ачт
|
Энергетическая светимость тела по определению: или для тела равномерно излучающего со всей поверхности
где Энергетическая светимость абсолютно черного тела согласно
где Согласно закону смещения где Тогда температуру тела можно
Следовательно, площадь
|
|
Ответ: |
|
2. Увеличение температуры
равновесного излучения на ![]() К привело к изменению
К привело к изменению
наиболее вероятной длины волны в его спектре на ![]() нм.
нм.
Какова начальная температура ![]() равновесного излучения?
равновесного излучения?
|
Дано: |
Решение: |
|
|
Согласно закону смещения где Так как температура
Так как
Решим уравнение:
Т.к. температура
|
|
Ответ: |
|
3. Медный шарик радиусом ![]() мм с абсолютно черной поверхностью
мм с абсолютно черной поверхностью
поместили в откачанный сосуд, температура стенок которого поддерживается
близкой к абсолютному нулю ![]() К. Начальная температура
К. Начальная температура
шарика ![]() К. Через какое время
К. Через какое время ![]() его температура
его температура ![]() уменьшится
уменьшится
в ![]() раза? Удельная теплоемкость меди
раза? Удельная теплоемкость меди ![]() Дж/(кг∙К).
Дж/(кг∙К).
|
Дано: |
Решение: |
|
Шарик − ачт:
стенки сосуда:
|
Энергетическая светимость тела по определению: или для шарика равномерно излучающего со всей поверхности
Энергетическая светимость абсолютно черного тела согласно
где Тогда энергия, излучаемая с поверхности шарика за время
Т.к. шарик помещен в откачанный
знак «-» учитывает, что
Проинтегрируем последнее выражение:
Получим
|
|
Ответ: |
|
4. Какую мощность нужно
подводить к зачерненному металлическому шарику диаметром ![]() см, чтобы поддерживать его температуру на
см, чтобы поддерживать его температуру на ![]() К выше температуры окружающей среды?
К выше температуры окружающей среды?
Температура окружающей среды ![]() К. Считать, что тепло
К. Считать, что тепло
теряется только вследствие излучения.
|
Дано: |
Решение: |
|
Шарик − ачт:
|
Энергетическая светимость тела по определению: или для шарика равномерно излучающего со всей поверхности
где Энергетическая светимость абсолютно черного тела согласно
где Так как шарик можно Мощность излучения с поверхности шарика (энергия,
Так как шарик находится в среде с температурой
Чтобы поддерживать температуру шарика постоянной и
|
|
Ответ: |
|
5. Определить, с какой
скоростью ![]() должен двигаться и какую кинетическую
должен двигаться и какую кинетическую
энергию ![]() должен иметь электрон, чтобы его импульс
должен иметь электрон, чтобы его импульс
был равен импульсу фотона, длина волны которого ![]() пм.
пм.
|
Дано: |
Решение: |
|
|
Импульс фотона: Импульс электрона: 1) Так как
Решим квадратное уравнение:
Кинетическая энергия электронов
2) Так как
|
|
Ответ: |
|
6. Рубиновый лазер
излучает в импульсе длительностью ![]() мс энергию
мс энергию ![]() Дж в виде узкого, почти параллельного пучка
Дж в виде узкого, почти параллельного пучка
монохроматического света. Найти среднее за время импульса давление ![]() пучка света, если его сфокусировать в
пучка света, если его сфокусировать в
пятнышко диаметром ![]() мкм на поверхность,
мкм на поверхность,
перпендикулярную пучку, с коэффициентом отражения ![]() .
.
|
Дано: |
Решение: |
|
|
Давление света:
где
|
|
Ответ: |
|
7. Определить напряжение ![]() на
на
рентгеновской трубке и скорость электронов ![]() ,
,
подлетающих к аноду рентгеновской трубки, если длина волны коротковолновой
границы сплошного рентгеновского спектра ![]() нм.
нм.
|
Дано: |
Решение: |
|
Тормозное рентгеновское излучение
|
Кинетическая энергия электронов
Максимальная энергия фотона,
Следовательно, напряжение
кинетическая энергия электронов |
Решение: общая энергия теплового излучения определяется законом Стефана — Больцмана, который гласит: мощность излучения абсолютно чёрного тела, приходящаяся на единицу площади поверхности, прямо пропорциональна четвёртой степени температуры тела:
[ j=sigma cdot T^{4} ,{rm ; ; ; ; }j=frac{P}{S}. ]
Здесь P = 1 кВт – мощность излучения, S – искомая площадь,
σ = 5,67•10–8 Вт/(м²•К4) — постоянная Стефана — Больцмана.
Длина волны, при которой энергия излучения абсолютно чёрного тела максимальна, определяется законом смещения Вина:
[ lambda _{max } =frac{b}{T} ,{rm ; ; ; ; }T=frac{b}{lambda _{max }}. ]
Коэффициент b =0,002898 м•К – постоянная Вина. Тогда искомая площадь
[ frac{P}{S} =sigma cdot left(frac{b}{lambda _{max } } right)^{4} ,{rm ; ; ; ; }S=frac{P}{sigma } cdot left(frac{lambda _{max } }{b} right)^{4} . ]
Ответ: 1,1•10-3 м2 = 11 см2.
Спектральная
излучательная способность
![]()
(или
![]()
)
(спектральная плотность энергетической
светимости) – энергия, излученная
нагретым телом в единицу времени с
единицы площади в единичном диапазоне
частот
(или в единичном диапазоне длин волн
)
Энергетическая
светимость
![]()
–
энергия, излученная нагретым телом в
единицу времени с единицы площади во
всем диапазоне частот (или длин волн).
Графически интегрирование спектральной
излучательной способности – это
нахождение площади под кривой
![]()
или
![]()
.
Спектральная
поглощательная способность аТ
(степень черноты) –
отношение поглощенной телом энергии к
энергии, падающей на тело (в единичном
интервале частот). У абсолютно черного
тела аТ
=
1.
Закон
Стефана-Больцмана: энергетическая
светимость абсолютно черного тела
пропорциональна абсолютной температуре
в четвертой степени, т.е.
![]()
, (9.1)
где
σ = 5,67∙10–8
Вт/(м2К4)
– постоянная Стефана-Больцмана.
Для
серого тела можно записать аналогичное
выражение:
![]()
, (9.2)
где
А
–
коэффициент черноты (или коэффициент
серости).
Закон
Вина:
длина волны, на которую приходится
максимум спектральной излучательной
способности абсолютно черного тела,
обратно пропорциональна абсолютной
температуре этого тела, т.е.
![]()
, (9.3)
где
b
= 2,9∙10–3
м∙К – постоянная Вина.
Задача
14
Поток
энергии, излучаемой из смотрового окошка
плавильной печи площадью S
равен Ф. Принимая, что отверстие печи
излучает, как черное тело определить
температуру печи. . Ф
= 100 Вт;
S
= 10 см2.
Решение:
Поток
излученной энергии Ф – это энергия,
излученная телом за одну секунду. Тогда
энергетическая светимость – это
плотность потока излученной энергии,
т.е
![]()
.
Используя закон Стефана-Больцмана
(9.1), найдем температуру в печи:
![]()
К
Ответ:
1152 К
Задача
15
Исследование
спектра излучения некоторой звезды
показывает, что максимум спектральной
плотности энергетической светимости
соответствует длине волны λ = 100 нм.
Принимая звезду за абсолютно черное
тело определить ее энергетическую
светимость. (ГВт/м2).
Решение:
Из
закона смещения Вина (9.3) найдем абсолютную
тепреатуру поверхности звезды:
![]()
К (9.4)
Подставляя
(9.4) в (9.1) получим энергетическую
светимость:
![]()
Вт/м2
Ответ:
40,1 ГВт/м2
9-1.
Чему равна длина волны, на которую
приходится максимум излучения абсолютно
черного тела с температурой Т. (Ответ
дать в мкм). Т = 1000 К.
Ответ:
2,9 мкм
9-2.
Длина волны, на которую приходится
максимум излучения абсолютно черного
тела, равна λ. Определить температуру
тела. (Ответ дать в оС).
λ = 1 мкм.
Ответ:
2627С
9-3.
Черное тело находится при температуре
Т1.
При остывании тела длина волны,
соответствующая максимуму спектральной
плотности энергетической светимости,
изменилась на Δλ. Определить температуру
Т2
до которой тело охладилось. (Ответ дать
в оС).
Т1
= 104
К; Δλ = 1 мкм
Ответ:
1975С
9-4.
Черное тело нагрели от температуры Т1
до Т2.
Определить на сколько уменьшилась длина
волны, соответствующая максимуму
спектральной плотности энергетической
светимости. (Ответ дать в мкм). Т1
= 100К; Т2
= 1000 К
Ответ:
26,1 мкм
9-5.
На сколько увеличится энергетическая
светимость абсолютно черного тела, если
его температуру увеличить на х%. (Ответ
дать в %). х = 1%
Ответ:
4,1 %
9-6.
Определить диаметр нити накала
электрической лампы, если мощность
электрического тока, питающего лампу
равна Р, длина нити – l,
температура – Т.
Считать, что излучение нити соответствует
излучению абсолютно черного тела. (Ответ
дать в мм). Р = 1000 Вт; l
= 10 см; Т
= 3000 К
Ответ:
0,69 мм
9-7.
Какой поток энергии получает комната
через открытую дверцу в которой
поддерживается температура Т?
Размер дверцы аd.
Считать, что отверстие печи излучает
как черное тело. а
= 10 см; d
=
15 см; Т
= 1000 К
Ответ:
850,5 Вт
9-8.
С поверхности сажи площадью S
при температуре Т
за время t
излучается энергия W.
Определить коэффициент черноты сажи.
S
= 1 см2;
Т = 400С;
W
= 1000 Дж; t
= 1 мин
Ответ:
0,14
9-9.
Мощность излучения шара радиусом R
при некоторой постоянной температуре
равен Р.
Найти эту температуру Т,
считая шар серым телом с коэффициентом
черноты αт.
(Ответ дать в К). R
= 10 см; Р
= 1 кВт; αт
= 0,1
Ответ:
1088 К

9-10.
Площадь, ограниченная графиком
спектральной плотности
энергетической светимости rω,т
черного тела, при переходе от
термодинамической температуры Т1
к температуре Т2
увеличилась в n
раз. Во сколько раз возросла температура?
n
= 16
Ответ:
2

9-11.
Площадь,
ограниченная графиком спектральной
плотности энергетической светимости
rλ,т
абсолютно черного тела, при переходе
от термодинамической температуры Т1
к температуре Т2
увеличилась в n
раз. Найдите отношение длин волн
![]()
,
соответствующих максимумам спектральной
плотности энергетической светимости
черного тела при этих температурах. n
= 4
Ответ:
1,41
9-12.
Длина волны, на которую приходится
максимум излучения шара радиусом R,
равна .
Найти мощность излучения шара, считая
его черным телом. R
= 10 см;
= 100 мкм.
Ответ:
5 мВт
9-13.
Мощность излучения квадрата со стороной
а
равно Р. Считая квадрат черным телом
определить длину волны на которую
приходится максимум излучения. (Ответ
дать в мкм). Р = 1000 Вт; а
= 10 см.
Ответ:
2,52 мкм
9-14.
Определить длину цилиндра радиуса R,
если с его поверхности за время t
излучается энергия W.
Длина волны на которую приходится
максимум излучения равна .
Считать цилиндр серым телом с коэффициентом
черноты αт.
R
= 10 см; t
= 1 с; W
= 100 Дж, λ = 10 мкм; αт
= 0,4.
Ответ:
0,892 м
9-15.
Определить во сколько раз увеличится
мощность излучения черного тела, если
длина волны, соответствующая максимуму
его спектральной плотности энергетической
светимости сместится с λ1
= 200 мкм до λ2
= 100 мкм.
Ответ:
16
9-16.
Энергетическая светимость черного тела
равна R
=
100 МВт/м2.
Определить длину волны, соответствующую
максимуму спектральной плотности
энергетической светимости этого тела.
(Ответ дать в нм).
Ответ:
447,5 нм
9-17.
Диаметр спирали в электрической лампочке
равен d,
длина спирали – l.
При включении лампочки в цепь напряжением
U
через лампочку течет ток силой I.
Найти температуру лампочки. Считать,
что по установлении равновесия все
выделяющееся тепло теряется в результате
лучеиспускания. Отношение энергетических
светимостей спирали и абсолютно черного
тела считать для этой температуры равным
n.
(Ответ дать в К).
d
= 0,1 мм; l
= 10 см; U
= 100 В; I
= 0,1 А; n
= 0,31;
Ответ:
2063 К
9-18.
Какое количество энергии излучает
абсолютно черное тело с площади S
за время t,
если известно, что максимум спектральной
плотности энергетической светимости
этого тела приходится на длину волны
λ. (Ответ дать в МДж). S
= 1 см2;
t
= 1 с; λ = 100 нм.
Ответ:
4,01 МДж
9-19.
Мощность излучения абсолютно черного
тела равна Р.
Найти площадь излучающей поверхности
тела, если известно, что длина волны, на
которую приходится максимум спектральной
плотности энергетической светимости
этого тела, равна λ. (Ответ дать в мм2).
Р
= 1 кВт; λ = 1 мкм.
Ответ:
249 мм2
9-20.
Диаметр спирали в электрической лампочке
равен d,
длина спирали – l.
При включении лампочки в цепь напряжением
U
через лампочку течет ток силой I.
Принимая, что излучение нити соответствует
излучению абсолютно черного тела,
определить ее энергетическую светимость.
(Ответ дать в МВт/м2).
I
=
0,1 А; U
= 100 В; d
=
0,1 мм; l
= 10 см.
Ответ:
0,318 МВт/м2
9-21.
Энергия излучения абсолютно черного
тела за время t
равна W.
Найти площадь излучающей поверхности
тела, если известно, что максимальная
спектральная плотность его энергетической
светимости приходится на длину волны
λ. (Ответ дать в мм2).
W
= 100 Дж; t
= 1с; λ = 1 мкм.
Ответ:
24,94 мм2
9-22.
Энергия излучения шара площадью S
за время t
равна W.
Найти температуру шара, считая, что
отношение энергетических светимостей
шара и абсолютно черного тела для этой
температуры равным n.
(Ответ дать в К). S
= 1 см2;
W
= 1 кДж; t
= 1с;
n
= 0,1
Ответ:
6480 К
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Найти площадь S излучающей поверхности нити
|
Условие задачи Найти площадь S излучающей поверхности нити 25-ваттной лампы, если температура нити Т = 2450 К. Излучение нити составляет р = 30% излучения абсолютно чёрного тела при данной температуре. Потерями тепла, связанными с теплопроводностью, пренебречь. Решение задачи
|
Категория: Задачи | Добавил: Creator (23.07.2016) |
| Просмотров: 5371 | Теги: температура, Абсолютно, поверхность, нить, площадь, тело, Черное, теплопроводность, лампа | Рейтинг: 0.0/0 |
Законы теплового излучения. Лучистое тепло.
Страница: 1 / Страница: 2
Может, для кого-то это будет новостью, но передача температуры происходит не только теплопроводностью через прикосновение одного тела к другому. Каждое тело (Твердое, жидкое и газообразное) испускает тепловые лучи определенной волны. Эти лучи, уходя от одного тела, поглощаются другим телом, и принимают тепло на себя. И я попытаюсь Вам объяснить, как это происходит, и сколько тепла мы теряем этим излучением у себя дома на отопление. (Я думаю, многим будет интересно увидеть эти цифры). В конце статьи решим задачку из реального примера.
В статье будут трехэтажные формулы и интегральные выражения для математиков, но не стоит их бояться, можете даже не вникать в эти формулы. В задаче я вам дам формулы, которые решаются на-раз-два и даже не нужно знать высшую математику, достаточно знать элементарную арифметику.

Я не однократно в этом убеждался, что сидя у костра (обычно большого) мое лицо обжигали эти лучи. И если я закрывал костер своими ладонями и при этом руки были вытянуты, то получалось, что мое лицо переставало обжигать. Не трудно догадаться, что эти лучи прямые как световые. Меня обжигает не воздух, циркулирующий вокруг костра, и даже не теплопроводность воздуха, а именно прямые не видимые тепловые лучи, идущие от костра.
В космосе между планетами обычно вакуум и поэтому передача температур осуществляется исключительно тепловыми лучами (Все лучи – это электромагнитные волны).
Тепловое излучение имеет природу такую, как световые и электромагнитные лучи (волны). Просто, эти волны (лучи) имеют разную длину волны.
Например, длины волн в диапазоне 0,76 – 50 мкм, называется инфракрасными. Все тела, имеющие комнатную температуру + 20 °С, излучают в основном инфракрасные волны с длинами волн, близкими к 10 мкм.
Всякое тело, если только температура его отлична от абсолютного нуля (-273,15 °С), способно посылать в окружающее пространство излучение. Поэтому любое тело излучает на окружающие его тела лучи и в свою очередь находится под воздействием излучения этих тел.
Любая мебель в доме (стул, стол, стены и даже диван) испускает тепловые лучи.
Тепловое излучение может поглощаться или проходить в сквозь тело, а также может просто отражаться от тела. Отражение тепловых лучей подобно тому, как если бы световой луч отражался от зеркала. Поглощение теплового излучения подобно тому, как черная крыша сильно нагревается от солнечных лучей. А проникновение или прохождение лучей подобно тому, как лучи проходят в сквозь стекло или воздух. Наиболее распространенным в природе видом электромагнитного излучения является тепловое излучение.
Очень близко по своим свойствам к черному телу относится так называемое реликтовое излучение, или космический микроволновой фон — заполняющее Вселенную излучение с температурой около 3 К.
Вообще в науке теплотехнике, чтобы объяснить процессы тепловых излучений, удобно использовать понятие черного тела, для того чтобы качественно объяснить процессы тепловых излучений. Только черное тело способно в некотором роде облегчить расчеты.
Как было описано выше любое тело способно:
1. Излучать тепловую энергию.
2. Поглощать тепловую энергию.
3. Отражать тепловую энергию.
Черное тело – это тело, которое полностью поглощает тепловую энергию, то есть оно не отражает лучи и в сквозь нее не проходит тепловое излучение. Но не забываем, что черное тело излучает тепловую энергию.
Поэтому к этому телу так легко применить расчеты.
Какие возникают сложности при расчете, если тело не является черным телом?
Тело, которое не является черным телом, имеет такие факторы:
1. Поглощает, какую-то часть теплового излучения, а другая часть проходит в сквозь тело.
2. Отражает, какую-то часть теплового излучения.
Эти два фактора усложняют расчет на столько, что “мама не горюй”. Очень сложно так считать. А ученые по этому поводу толком не объяснили, как рассчитать серое тело. Кстати серое тело – это и есть тело, которое не является черным телом.
Также есть понятие: Белое тело и прозрачное тело, но об этом ниже.
Тепловое излучение имеет разные частоты (разные волны), и каждое отдельное тело может иметь разную волну излучения. К тому же при изменении температуры, эта длина волны может меняться, может меняться и ее интенсивность (сила излучения).
Все эти факторы усложнят процесс на столько, что трудно подобрать универсальную формулу для расчета потерь энергии на излучательности. И поэтому в учебниках и в любых литературах используют для расчета черное тело, а другие серые тела используют как часть черного тела. Чтобы рассчитать серое тело используют коэффициент черноты. Эти коэффициенты приведены в справочниках для некоторых матералов.
Рассмотрим изображение, которое подтверждает сложность вычисления излучательности.

На рисунке изображены два шарика, которые в себе имеют частички этого шарика. Красные стрелки это лучи испускаемые частичками.
Рассмотрим черное тело.
Внутри черного тела глубоко внутри расположены некоторые частички, которые обозначены оранжевым цветом. Они испускают лучи, которые поглощают рядом находящиеся другие частички, которые обозначены желтым цветом. Лучи оранжевых частичек черного тела не способны пройти в сквозь другие частички. И поэтому только наружные частички этого шарика испускают лучи по всей площади шарика. Поэтому расчет черного тела легко считается. Также принято считать, что черное тело испускает весь спектр волн. То есть испускает все имеющиеся волны различных длин. Серое тело может испускать часть спектра волн, только определенной длины волн.
Рассмотрим серое тело.
Внутри серого тела, имеющиеся внутри частички излучают какую то часть лучей, которые проходят в сквозь другие частички. И только поэтому расчет усложняется многократно.
Тепловое излучение – это электромагнитное излучение, возникающее вследствие преобразования энергии теплового движения частиц тела в энергию излучения. Именно тепловой характер возбуждения элементарных излучателей (атомов, молекул и т.п.) противопоставляет тепловое излучение всем другим видам свечения и обуславливает его специфическое свойство зависеть лишь от температуры и оптических характеристик излучающего тела.
Опыт показывает, что тепловое излучение наблюдается у всех тел при любой температуре, отличной от 0 К. Конечно, интенсивность и характер излучения зависят от температуры излучающего тела. Например, все тела, имеющие комнатную температуру + 20 °С, излучают в основном инфракрасные волны с длинами волн, близкими к 10 мкм, а Солнце излучает энергию, максимум которой приходится на 0,5 мкм, что соответствует видимому диапазону. При Т → 0 К тела практически не излучают.
Тепловое излучение ведет к уменьшению внутренней энергии тела и, следовательно, к снижению температуры тела, к охлаждению. Нагретое тело за счет теплового излучения отдает внутреннюю энергию и охлаждается до температуры окружающих тел. В свою очередь, поглощая излучение, могут нагреваться холодные тела. Такие процессы, которые могут происходить и в вакууме, называют радиационным теплообменом.
Абсолютно черное тело — физическая абстракция, применяемая в термодинамике, тело, поглощающее все падающее на него электромагнитное излучение во всех диапазонах и ничего не отражающее. Несмотря на название, абсолютно черное тело само может испускать электромагнитное излучение любой частоты и визуально иметь цвет. Спектр излучения абсолютно черного тела определяется только его температурой.
Таблица:
(Температурный интервал в Кельвинах и их Цвет)
до 1000 Красный
1000—1500 Оранжевый
1500—2000 Жёлтый
2000—4000 Бледно-жёлтый
4000—5500 Желтовато-белый
5500—7000 Чисто белый
7000—9000 Голубовато-белый
9000—15000 Бело-голубой
15000—∞ Голубой
Кстати по длине волны (цвета) определили температуру солнца оно около 6000 Кельвин. Угли обычно светятся красным цветом. Вам это ничего не напоминает? По цвету можно определять температуру. То есть существуют такие приборы, которые измеряют длину волны, тем самым определяют температуру материала.
Наиболее черные реальные вещества, например, сажа, поглощают до 99 % падающего излучения (т. е. имеют альбедо, равное 0,01) в видимом диапазоне длин волн, однако инфракрасное излучение поглощается ими значительно хуже. Глубокий черный цвет некоторых материалов (древесного угля, черного бархата) и зрачка человеческого глаза объясняется тем же механизмом. Среди тел Солнечной системы свойствами абсолютно черного тела в наибольшей степени обладает Солнце. По определению Солнце практически не отражает никакого излучения. Термин был введен Густавом Кирхгофом в 1862.
По спектральной классификации Солнце относится к типу G2V («жёлтый карлик»). Температура поверхности Солнца достигает 6000 K, поэтому Солнце светит почти белым светом, но из-за поглощения части спектра атмосферой Земли у поверхности нашей планеты этот свет приобретает жёлтый оттенок.
Абсолютно чёрное тела – 100% поглощает и при этом нагревается, так и наоборот! нагретое тело – 100% излучает это означает, что есть строгая закономерность (формула излучения абсолютно чёрного тела) между температурой Солнца – и его спектром – так как и спектр и температуру уже определили – да, у Солнца нет отклонений от этих параметров!
В астрономии есть такая диаграмма – “Спектр-Светимость”, так вот наше Солнце принадлежит “главной последовательности” звезд, к которой принадлежат и большинство других звезд, то есть почти все звезды “абсолютно чёрные тела”, как это не странно… Исключения – белые карлики, красные гиганты и Новые, Сверх-Новые…
Это кто-то физику в школе недоучил.
Абсолютно чёрное тело поглощает ВСЁ излучение и излучает больше всех остальных тел (чем больше тело поглощает, тем сильнее оно нагревается; чем больше оно нагревается, тем больше оно излучает).
Пусть у нас есть две поверхности – серая (с коэффициентом черноты 0,5) и абсолютно чёрная (коэффициент 1).
Коэффициент черноты – это коэффициент поглощения.
Теперь на эти поверхности направив одинаковый поток фотонов, допустим, 100 штук.
Серая поверхность поглотит 50 из них, чёрная – все 100.
Какая поверхность, испускает больше света – в которой “сидит” 50 фотонов или 100?
Излучение абсолютно чёрного тела впервые правильно рассчитал Планк.
Излучение Солнца примерно подчиняется формуле Планка.
И так начнем изучать теорию…
Под излучением (радиацией) понимают испускание и распространение электромагнитных волн любого вида. В зависимости от длины волны различают: Ренгеновские, ультрафиолетовые, инфракрасные, световое (видимое) излучение и радиоволны.
Рентгеновское излучение — электромагнитные волны, энергия фотонов которых лежит на шкале электромагнитных волн между ультрафиолетовым излучением и гамма-излучением, что соответствует длинам волн от 10−2 до 103 Ангстрем. 10 Ангстрем = 1 нм. (0,001-100 нм)
Ультрафиолетовое излучение (ультрафиолет, УФ, UV) — электромагнитное излучение, занимающее диапазон между фиолетовой границей видимого излучения и рентгеновским излучением (10 — 380 нм).
Инфракрасное излучение — электромагнитное излучение, занимающее спектральную область между красным концом видимого света (с длиной волны λ = 0,74 мкм) и микроволновым излучением (λ ~ 1—2 мм).
Сейчас весь диапазон инфракрасного излучения делят на три составляющих:
Коротковолновая область: λ = 0,74—2,5 мкм;
Средневолновая область: λ = 2,5—50 мкм;
Длинноволновая область: λ = 50—2000 мкм;
Видимое излучение — электромагнитные волны, воспринимаемые человеческим глазом. Чувствительность человеческого глаза к электромагнитному излучению зависит от длины волны (частоты) излучения, при этом максимум чувствительности приходится на 555 нм (540 терагерц), в зелёной части спектра. Поскольку при удалении от точки максимума чувствительность спадает до нуля постепенно, указать точные границы спектрального диапазона видимого излучения невозможно. Обычно в качестве коротковолновой границы принимают участок 380—400 нм (750—790 ТГц), а в качестве длинноволновой — 760—780 нм (385—395 ТГц). Электромагнитное излучение с такими длинами волн также называется видимым светом, или просто светом (в узком смысле этого слова).
Радиоизлучение (радиоволны, радиочастоты) — электромагнитное излучение с длинами волн 5•10−5—1010 метров и частотами, соответственно, от 6•1012 Гц и до нескольких Гц. Радиоволны используются при передаче данных в радиосетях.
Тепловое излучение представляет собой процесс распространения в пространстве внутренней энергии излучающего тела путем электромагнитных волн. Возбудителями этих волн являются материальные частицы, входящие в состав вещества. Для распространения электромагнитных волн не требуется материальной среды, в вакууме они распространяются со скоростью света и характеризуются длиной волны λ или частотой колебаний ν. При температуре до 1500 °С основная часть энергии соответствует инфракрасному и частично световому излучению (λ=0,7÷50 мкм).
Следует отметить, что энергия излучения испускается не непрерывно, а в виде определенных порций — квантов. Носителями этих порций энергии являются элементарные частицы излучения — фотоны, обладающие энергией, количеством движений и электромагнитной массой. При попадании на другие тела энергия излучения частично поглощается ими, частично отражается и частично проходит сквозь тело. Процесс превращения энергии излучения во внутреннюю энергию поглощающего тела называется поглощением. Большинство твердых и жидких тел излучают энергию всех длин волн в интервале от 0 до ∞, то есть имеют сплошной спектр излучения. Газы испускают энергию только в определенных интервалах длин волн (селективный спектр излучения). Твердые тела излучают и поглощают энергию поверхностью, а газы — объемом.
Излучаемая в единицу времени энергия в узком интервале изменения длин волн (от λ до λ+dλ) называется потоком монохроматического излучения Qλ. Поток излучения, соответствующий всему спектру в пределах от 0 до ∞, называется интегральным, или полным, лучистым потоком Q(Вт). Интегральный лучистый поток, излучаемый с единицы поверхности тела по всем направлениям полусферического пространства, называется плотностью интегрального излучения (Вт/м2).

Чтобы понять эту формулу рассмотрим изображение.


Я не случайно изобразил два варианта тела. Формула справедлива только для тела квадратной формы. Так как излучающая площадь должна быть плоской. При условии, что излучает только поверхность тела. Внутренние частицы не излучают.
S - площадь тела (м2)
Q - энергия (Вт), излучаемая лучами со всей площади.
Зная плотность излучения материала, можно рассчитать, сколько энергии уходит на излучение:
Q=E•S
Необходимо понимать, что лучи исходящие от плоскости имеют разную интенсивность излучения по отношению к нормали плоскости.
Закон Ламберта. Излучаемая телом лучистая энергия распространяется в пространстве по различным направлениям с различной интенсивностью. Закон, устанавливающий зависимость интенсивности излучения от направления, называется законом Ламберта.
Закон Ламберта устанавливает, что количество лучистой энергии, излучаемое элементом поверхности в направлении другого элемента, пропорционально произведению количества энергии, излучаемой по нормали, на величину пространственного угла, составленного направлением излучения с нормалью
Смотри изображение.

Интенсивность каждого лучика можно найти с помощью тригонометрической функции:
Qх=Q•sin Y
То есть [sin Y] – это своего рода коэффициент угла и он строго подчиняется тригонометрии угла. Коэффициент работает только для черного тела. Так как рядом находящиеся частички будут поглощать боковые лучи. Для серого тела, необходимо учитывать количество проходящих в сквозь частички лучей. Отражение лучей, тоже необходимо учитывать.
Следовательно, наибольшее количество лучистой энергии излучается в перпендикулярном направлении к поверхности излучения. Закон Ламберта полностью справедлив для абсолютно черного тела и для тел, обладающих диффузным излучением при температуре 0 – 60°С. Для полированных поверхностей закон Ламберта неприменим. Для них лучеиспускание при угле будет большим, чем в направлении, нормальном к поверхности.
Ниже мы обязательно рассмотрим более объемные формулы для расчета количества тепла теряемые телом. Но пока необходимо кое-что узнать дополнительно о теории.
Немного об определениях. Определения пригодятся, чтобы правильно выражаться.
Отметим, что большинство твердых и жидких тел имеет сплошной (непрерывный) спектр излучения. Это значит, что они обладают способностью излучать лучи всех длин волн.
Даже обычный стол в комнате как твердое тело может излучать рентгеновское или ультрафиолетовое излучение, но интенсивность его настолько мала, что мы этого не то, что не замечаем, его значение по отношению к другим волнам может приближаться к нулевому значению.
Лучистым потоком (или потоком излучения) называют отношение лучистой энергии ко времени излучения, Вт:
Ф= ΔQ/Δt,
где Q— энергия излучения, Дж; т — время, с.
Если лучистый поток, излучаемый произвольной поверхностью во всех направлениях (т.е. в пределах полусферы произвольного радиуса) осуществляется в узком интервале длин волн от λ до λ+Δλ, то его называют потоком монохроматического излучения
Ф=ΔQλ/Δt
Суммарное излучение с поверхности тела по всем длинам волн спектра называется интегральным или полным потоком излучения Ф
Интегральный поток, испускаемый с единицы поверхности, носит название поверхностной плотности потока интегрального излучения или излучательности, Вт/м2,
Е = ΔФ/ΔА
Формулу можно применять и при монохроматическом излучении. Если на поверхность тела падает тепловое монохроматическое излучение, то в общем случае часть, равная Вλ этого излучения, поглотится телом, т.е. превратится в другую форму энергии в результате взаимодействия с веществом, часть Fλ будет отражена, и часть Dλ пройдет сквозь тело. Если принять, что падающее на тело излучение равно единице, то
Вλ+Fλ+Dλ=1
где Вλ, Fλ, Dλ — коэффициенты соответственно поглощения, отражения
и пропускания тела.
Когда в пределах спектра величины В, F, D остаются постоянными, т.е. не зависят от длины волны, то надобность в индексах отпадает. В этом случае
B+F+D = 1,
Если В= 1 (F = D = 0), то тело, полностью поглощающее все падающее на него излучение независимо от длины волны, направления падения и состояния поляризации излучения, называется черным телом или полным излучателем.
Если F=1 (В=D=0), то падающее на тело излучение полностью отражается. В том случае, когда поверхность тела шероховатая, то лучи отражаются рассеянно (диффузное отражение), и тело называют белым, а когда поверхность тела гладкая и отражение следует законам геометрической оптики, то тело (поверхность) называют зеркальным. В том случае, когда D = 1 (В=F=0), тело проницаемо для тепловых лучей (диатермично).
Твердые тела и жидкости для тепловых лучей практически непрозрачны (D = 0), т.е. атермичны. Для таких тел
В + F= 1.
Этот фактор упрощает расчеты, так как там где мы живем, обычно нас окружают твердые тела. А также твердые тела обычно испускают весь спектр волн (частот). Для будущей задачи мы примем эти показатели во внимание.
Абсолютно черных, так же как и прозрачных или белых тел, в природе нет. Такие тела должны рассматриваться как научные абстракции. Но все же некоторые реальные тела могут достаточно близко подходить по своим свойствам к таким идеализированным телам.
Надо отметить, что некоторые тела обладают по отношению к лучам определенной длины волны одними свойствами, а к лучам другой длины — иными. Например, тело может быть прозрачным для инфракрасных лучей и непрозрачным для видимых (световых) лучей. Поверхность тела может быть гладкой по отношению к лучам одной длины волны и шероховатой — для лучей другой длины волны.
Газы, в особенности находящиеся под небольшим давлением, в противоположность твердым и жидким телам излучают линейчатый спектр. Таким образом, газы поглощают и излучают лучи лишь определенной длины волны, других же лучей они не могут ни излучать, ни поглощать. В этом случае говорят о селективном (выборочном) поглощении и излучении.
В теории теплового излучения важную роль играет величина, называемая спектральной плотностью потока излучения, или спектральной излучательностью, представляющей собой отношение плотности лучистого потока, испускаемого в бесконечно малом интервале длин волн от λ до λ+Δλ, к размеру этого интервала длин волн Δλ, Вт/м2,
Eλ=ΔE/Δλ,
где E – поверхностная плотность лучистого потока, Вт/м2.
Теперь надеюсь Вам понятно, что процесс вычисления становится сверх затруднительным. Нам еще в этом направление работать и работать. Это каждый материал надо тестировать на различные температуры. Но почему-то данных по материалам практически нет. Вернее я не нашел эксперементальный справочник по материалам.
Почему нет такого справочника по материалам? Потому что теплопотери тепловым излучением очень маленькие, и я думаю вряд ли превышают 10% в наших бытовых условиях. Поэтому в расчет теплопотерь их не закладывают. Вот когда мы будем часто летать в космос, тогда и появятся все расчеты. Вернее в нашей космонавтике накопились данные по материалам, но в свободной доступности их пока нет.
Закон поглощения лучистой энергии
Каждое тело способно поглощать какую-либо часть излучающей энергии об этом ниже.

Если на какое-либо тело толщиной l, падает лучистый поток (смотри рисунок), то в общем случае при прохождении сквозь тело он уменьшается. Принимают, что относительное изменение лучистого потока на пути Δl прямо пропорционально пути потока:

Коэффициент пропорциональности b называется показателем погло-щения, зависящим в общем случае от физических свойств тела и длины волны.
Интегрируя в пределах от l до 0 и принимая b постоянным, получаем

Установим связь между спектральным коэффициентом поглощения тела Вλ и спектральным показателем поглощения вещества bλ.
Из определения спектрального коэффициента поглощения Вλ имеем

После подстановки в это уравнение значения получим соотношение между спектральным коэффициентом поглощения Вλ и спектральным показателем поглощения Bλ.

Коэффициент поглощения Вλ равен нулю при l1= 0 и bλ = 0. При большом значении bλ достаточно весьма малого значения l, но все же не равного нулю, чтобы значение Вλ было как угодно близко к единице. В этом случае можно говорить, что поглощение происходит в тонком поверхностном слое вещества. Только в этом понимании возможно говорить о поверхностном поглощении. Для большинства твердых тел благодаря большому значению показателя поглощения bλ имеет место в ука-занном смысле «поверхностное поглощение», в связи с чем на коэффициент поглощения большое влияние оказывает состояние его поверхности.
Тела, хотя и с малым значением показателя поглощения, как, например, газы, могут при их достаточной толщине обладать большим коэффициентом поглощения, т.е. делаются непрозрачными для лучей данной длины волны.
Если bλ=0 для интервала Δλ, а для остальных длин волн bλ не равно нулю, то тело будет поглощать падающее излучение только определен-ных длин волн. В этом случае, как было указано выше, говорят о селективном (выборочном) коэффициенте поглощения.
Подчеркнем принципиальную разницу между показателем поглоще-ния вещества bλ и коэффициентом поглощения Вλ тела. Первый характе-ризует физические свойства вещества по отношению к лучам определенной длины волны. Значение Вλ зависит не только от физических свойств вещества, из которого состоит тело, но и от формы, размеров и состояния поверхности тела.
Законы излучения лучистой энергии
Макс Планк теоретически на основе электромагнитной теории установил закон (носящий название закона Планка), выражающий зависимость спектральной излучательности черного тела Е0λ от длины волны λ и температуры Т.

где E0λ(λ,T) – излучательность черного тела, Вт/м2; T – термодинамическая температура, K; C1 и C2 – постоянные; С1=2πhc2=(3,74150±0,0003)•10-16 Вт•м2; С2=hc/k=(1,438790±0,00019)•10-2; м•K (здесь h=(6,626176±0,000036)•10-34 Дж•с – постоянная Планка; с=(299792458±1,2) м/с – скорость распространения электромагнитных волн в свободном пространстве: k – постоянная Больцмана.)
Из закона Планка следует, что спектральная излучательность может равняться нулю [E0λ(λ,Т)=0] при термодинамической температуре, равной нулю (Т=0), либо при длине волны λ = 0 и λ→∞ (при Т≠0).
Следовательно, черное тело излучает при любой температуре больше 0 К. (Т > 0) лучи всех длин волн, т.е. имеет сплошной (непрерывный) спектр излучения.
Из выше указанной формулы можно получить расчетное выражение для излучательности черного тела:

Интегрируя в пределах изменения λ от 0 до ∞ получаем

В результате разложения подынтегрального выражения в ряд и его интегрирования получают расчетное выражение для излучательности черного тела, называемое законом Стефана—Больцмана:

где Е0 – излучательность черного тела, Вт/м2;
σ — постоянная Стефана Больцмана, Вт/(м2 •К4);
σ = (5,67032 ± 0,00071)•10-8;
Т- термодинамическая температура, К.
Формулу часто записывают в более удобной для расчета форме:

Эту формулу мы будем использовать для расчетов. Но это не окончательная формула. Она справедлива только для черных тел. О том как использовать для серых тел будет описано ниже.
где E0 – коэффициент излучения черного тела; С0 = 5,67 Вт/(м2 •К4).
Закон Стефана—Больцмана формулируют так: излучательность чер-ного тела прямо пропорциональна его термодинамической температуре в четвертой степени.
Спектральное распределение излучения черного тела при различных температурах

λ – длина волны от 0 до 10 мкм (0-10000 нм)
E0λ – следует понимать так: Как если бы в объеме (м3) черного тела находиться определенное количество энергии (Вт). Это не означает, что оно излучает такую энергию только наружными частичками. Просто если собрать все частички черного тела в объеме и измерить каждой частички излучаетельность во всех направлениях и сложить их все, то мы получим полную энергию на объеме, которая и указана на графике.
Как видно из расположения изотерм, каждая из них имеет максимум, причем, чем больше термодинамическая температура, тем больше значение E0λ, отвечающее максимуму, а сама точка максимума перемещается в область более коротких волн. Перемещение максимальной спектральной излучательности E0λmax в область более коротких волн известно под названием
закона смещения Вина, по которому
T•λmax = 2,88•10-3 м•К = const и λmax = 2,88•10-3/Т,
где λmax – длина волны, соответствующая максимальному значению спектральной излучаетльности E0λmax.
Так, например, при Т = 6000 К (примерная температура поверхности Солнца) максимум Е0λ располагается в области видимого излучения, на которую падает около 50% излучательности Солнца.
Элементарная площадка под изотермой, заштрихованная на графике равна Е0λ Δλ. Ясно, что сумма этих площадок, т.е. интеграл представляет собой излучательность черного тела E0. Следовательно, площадь между изотермой и осью абсцисс изображает в условном масштабе диаграммы излучательность черного тела. При небольших значениях термодинамической температуры изотермы проходят в непосредственной близости к оси абсцисс, и указанная площадь становится столь малой, что практически ее можно считать равной нулю.
Большую роль в технике играют понятия о так называемых серых телах и сером излучении. Серым называется неселективный тепловой излучатель, способный излучать сплошной спектр, со спектральной излучательностыо Eλ для волн всех длин и при всех температурах, составляющей неизменную долю от спектральной излучательности черного тела Е0λ т.е.

Постоянная ε называется коэффициентом черноты теплового излучателя. Для серых тел коэффициент черноты ε < 1 и не зависит ни от температуры, ни от длины волны. Для черного тела ε = 1 .
На графике схематически показаны кривые распределения по длинам волн спектральной излучательности абсолютно черного тела Еλ(ε = 1) и спектральной излучательности серого тела Еλ той же температуры, что и черное тело (при ε = 0,5 и ε = 0,25). Излучательность серого тела

Произведение

называется коэффициентом излучения серого тела.

Полученные из опыта значения коэффициента излучения даны в справочной литературе.
Большинство тел, применяемых в технике, могут быть приняты за серые тела, и их излучение — за серое излучение. Более точные исследования показывают, что это возможно только в первом приближении, однако достаточно для практических целей. Отклонение от закона Стефана— Больцмана для серых тел обычно учитывается тем, что коэффициент излучения С принимают зависящим от температуры. В связи с этим в таблицах указывается интервал температур, для которых экспериментально определено значение коэффициента излучения С.
В дальнейшем для упрощения выводов будем считать, что коэффициент излучения серого тела не зависит от температуры.
Коэффициенты черноты некоторых материалов
(Материал / Температура в °С / Величина Е)
Алюминий окисленный / 200—600 / 0,11 —0,19
Алюминий полированный / 225—575 / 0,039—0,057
Кирпич красный / 20 / 0,93
Кирпич огнеупорный / – / 0,8—0,9
Медь окисленная / 200—600 / 0,57—0,87
Свинец окисленный / 200 / 0,63
Сталь окисленная / 200—600 / 0,8
Сталь шлифованная / 940-1100 / 0,55—0,61
Чугун обточенный / 830—910 / 0,6—0,7
Чугун окисленный / 200—600 / 0,64—0,78
Алюминий полированный / 50—500 / 0,04—0,06
Бронза / 50 / 0,1
Железо листовое оцинкованное, блестящее / 30 / 0,23
Жесть белая, старая / 20 / 0,28
Золото полированное / 200 – 600 / 0,02—0,03
Латунь матовая / 20-350 / 0,22
Медь полированная / 50—100 / 0,02
Никель полированный / 200—400 / 0,07—0,09
Олово блестящее / 20—50 / 0,04—0,06
Серебро полированное / 200—600 / 0,02—0,03
Стальной листовой прокат / 50 / 0,56
Сталь окисленная / 200—600 / 0,8
Сталь сильно окисленная / 500 / 0,98
Чугунное литье / 50 / 0,81
Асбестовый картон / 20 / 0,96
Дерево строганое / 20 / 0,8—0,9
Кирпич огнеупорный / 500—1000 / 0,8—0,9
Кирпич шамотный / 1000 / 0,75
Кирпич красный, шероховатый / 20 / 0,88—0,93
Лак черный, матовый / 40—100 / 0,96—0,98
Лак белый / 40—100 / 0,8—0,95
Масляные краски различных цветов / 100 / 0,92—0,96
Сажа ламповая / 20—400 / 0,95
Стекло / 20—100 / 0,91—0,94
Эмаль белая / 20 / 0,9
Закон Кирхгофа
Закон Кирхгофа устанавливает зависимость между излучательностью и коэффициентом поглощения серого тела.
Рассмотрим два параллельных серых тела бесконечной протяженности с плоскими поверхностями площадью А каждое.
Бесконечно протяженная плоскость дает возможность приблизить расчеты по нахождению реального излучения на практических и теоретических опытах. При теоретических опытах находят реальное значение за счет интегральных выражений, а при опытах, большая плоскость приближает расчеты к реальным значениям. Тем самым, мы как бы, большой бесконечной плоскостью гасим влияние ненужных боковых и угловых излучений, которые улетают и не поглощаются экспериментальными пластинами.

E - Излучательность, Вт;
B - Коэффициент поглощения;
F - Коэффициент отражения;
D - Коэффициент пропускания;
T - Температура К.
То есть, если коэффициент умножить на излучательность, то получим результирующее значение излучения (Вт).
Можно положить, что все лучи, посылаемые одним телом, полностью попадают на другое. Примем, что коэффициенты пропускания этих тел D1 = D2 = 0 и между поверхностями двух плоскостей находится теплопрозрачная (диатермическая) среда. Обозначим через E1, B1, F1, T1, и E2, B2, F2, T2 соответственно излучательности, коэффициенты поглощения, отражения и температуры пов ерхностей первого и второго тел.

Поток лучистой энергии от поверхности 1 к поверхности 2 равен произведению излучательности поверхности 1 на ее площадь А, т.е. Е1•А, из которого часть Е1•В2•А поглощается поверхностью 2, а часть Е1•F2•А отражается обратно на поверхность 1. Из этого отраженного потока Е1•F2•А поверхность 1 поглощает E1•F2•B1•A и отражает E1•F1•F2•A. ИЗ отраженного потока энергии E1•F1•F2•A поверхность 2 вновь поглотит E1•F1•F2•B2•A и отразит E1•F1•F2•A и т.д.
Аналогично происходит передача лучистой энергии потоком Е2 от поверхности 2 к поверхности 1. В итоге поток лучистой энергии, поглощенный поверхностью 2 (или отданный поверхностью 1),

Поток лучистой энергии, поглощенной поверхностью 1 (или отданной поверхностью 2),

В окончательном итоге поток лучистой энергии, переданной поверхностью 1 к поверхности 2, будет равен разности лучистых потоков Ф1→2 и Ф2→1 т.е.

Полученное выражение справедливо при всех значениях температур Т1 и Т2 и, в частности, при Т1 = Т2. В последнем случае рассматриваемая система находится в динамическом тепловом равновесии, и на основании второго начала термодинамики необходимо положить Ф1→2 = Ф2→1 откуда следует
Е1В2 = Е2B1
или
Е1/В1 = Е2/В2 = const.
Далее положим, что поверхность 2 является черной. Тогда Е2= Е0 и В2 = В0=1. Принимая для простоты Е1=E и В1 = В, получаем

Полученное равенство носит название закона Кирхгофа: отношение излучательности тела к его коэффициенту поглощения для всех серых тел, находящихся при одной и той же температуре, одинаково и равно излучательности черного тела при той же температуре.
Если какое-либо тело имеет малый коэффициент поглощения, как например, хорошо полированный металл, то это тело имеет и малую излучательность. На этом основании для уменьшения потерь теплоты излучением во внешнюю среду теплоотдающие поверхности покрывают листами полированного металла для тепловой изоляции.
При выводе закона Кирхгофа рассматривалось серое излучение. Вывод останется справедливым и в том случае, если тепловое излучение обоих тел рассматривается только в некоторой части спектра, но однако имеет одинаковый характер, т.е. оба тела испускают лучи, длины волн которых лежат в одной и той же произвольной спектральной области. В предельном случае приходим к случаю монохроматического излучения. Тогда

т.е. для монохроматического излучения закон Кирхгофа должен быть сформулирован так: отношение спектральной излучательности какого-либо тела при определенной длине волны к его коэффициенту поглощения при той же длине волны одинаково для всех тел, находящихся при одинаковых температурах, и равно спектральной излучательности черного тела при той же длине волны и той же температуре.
Заключаем, что для серого тела В = ε, т.е. понятия «коэффициент поглощения» В и «коэффициент черноты» ε для серого тела совпадают. По определению коэффициент черноты не зависит ни от температуры, ни от длины волны, а следовательно, и коэффи-циент поглощения серого тела также не зависит ни от длины волны, ни от температуры.
Излучение газов
Излучение газов существенно отличается от излучения твердых тел. Поглощение и излучение газов — селективное (выборочное). Газы поглощают и излучают лучистую энергию только в определенных, довольно узких интервалах Δλ длин волн — так называемых полосах. В остальной части спектра газы не излучают и не поглощают лучистой энергии.
Двухатомные газы обладают ничтожно малой способностью поглощать лучистую энергию, а следовательно, и малой способностью ее излучать. Поэтому эти газы обычно считают диатермичными. В отличие от двухатомных газов многоатомные, в том числе и трехатомные газы, обладают значительной способностью излучать и поглощать лучистую энергию. Из трехатомных газов в области теплотехнических расчетов наибольший практический интерес представляют углекислый газ (CO2) и водяной пар (H2O), имеющие по три полосы излучения.
В отличие от твердых тел показатель поглощения для газов (конечно, в области полос поглощения) мал. Поэтому для газообразных тел уже нельзя говорить о «поверхностном» поглощении, так как поглощение лучистой энергии происходит в конечном объеме газа. В этом смысле поглощение и излучение газов называются объемными. Кроме того, показатель поглощения bλ для газов зависит от температуры.
По закону поглощения спектральный коэффициент поглощения тела может быть определен по:

Для газообразных тел эта зависимость несколько усложняется тем, что на коэффициент поглощения газа влияет его давление. Последнее объясняется тем, что поглощение (излучение) протекает тем интенсивнее, чем большее число молекул встретит луч на своем пути, а объемное число молекул (отношение числа молекул к объему) прямо пропорционально давлению (при t = const).
В технических расчетах газового излучения, обычно поглощающие газы (CO2 и H2O) входят как компоненты в состав смеси газов. Если давление смеси p, а парциальное давление поглощающего (или излучающего) газа рi , то в необходимо вместо l подставить величину рi•1. Величина рi•1, представляющая собой произведение давления газа на его толщину, носит название эффективной толщины слоя. Таким образом, для газов спектральный коэффициент поглощения

Спектральный коэффициент поглощения газа (в пространстве) зависит от физических свойств газа, формы пространства, его размеров и температуры газа. Тогда в соответствии с законом Кирхгофа спектральная излучательность

Излучательность в пределах одной полосы спектра

По этой формуле определяют излучательность газа в свободное пространство (пустоту). (Свободное пространство можно рассматривать как черное пространство при 0 К.) Но газовое пространство всегда ограничено поверхностью твердого тела, в общем случае имеющей температуру Тст ≠ Тг и коэффициент черноты εст < 1. Следовательно, оболочка обладает собственным излучением (обычно в пределах всех длин волн), часть которого (в пределах полос Δλ.) поглощается газом.
Излучательность газа в замкнутом пространстве равна сумме излучательностей, взятых по всем полосам спектра:

Опытные исследования показали, что излучательность газов не следует закону Стефана— Больцмана, т.е. зависимости от четвертой степени абсолютной температуры.
Однако для практических расчетов излучения газов пользуются законом четвертых степеней, вводя соответствующую поправку в значение коэффициента черноты газа εг:

Здесь εг = f(T,p•l)
Средняя длина пути луча
l=3,6 V/A
где V- газовый объем; А – площадь поверхности оболочки.
Излучательность газа, компонентами которого являются CO2 и H2O (газообразные продукты сгорания), к оболочке серого тела

в которой последний член учитывает собственное излучение оболочки.
Так называемый эффективный коэффициент черноты оболочки ε’ст, больший, чем εст, в связи с наличием излучающего газа.
Коэффициент черноты газа при температуре газа tг

Значения степени черноты εCO2 и εH2O в зависимости от температуры при различных значениях параметра pil приведены на рисунке.


Поправочный коэффициент β определяют по графику.

Полосы излучения и поглощения для С02 и Н20 несколько перекрывают одна другую, в связи с чем часть энергии, излучаемой одним газом, поглощается другим. Поэтому коэффициент черноты смеси углекислого газа и водяного пара при температуре стенки tст

где Δεг — поправка, учитывающая указанное поглощение. Для газообразных продуктов сгорания обычного состава Δεг = 2 – 4% и ею можно пренебречь.
Можно принять, что при εст = 0,8 + 1,0 эффективный коэффициент черноты оболочки ε’ст = 0,5(εст + 1).
Указанные особенности излучения и поглощения газов позволяют установить механизм так называемого «парникового эффекта», который оказывает существенное влияние на формирование и изменение климата Земли.
Большая часть солнечной радиации проходит сквозь атмосферу и нагревает поверхность Земли. В свою очередь Землей испускается инфракрасное излучение, в результате чего она охлаждается. Однако часть это го излучения поглощается многоатомными («парниковыми») газами атмосферы, которая вследствие этого играет роль «одеяла», удерживающего теплоту. При этом наибольшее влияние на глобальное потепление оказывают такие «парниковые» газы, как двуокись углерода (55%), фреоны и родственные им газы (25%), метан (15%) и др.
На следующей странице еще будут затронуты некоторые законы. Также будет детальное пояснения как происходит тепловое излучение через окно. Будут описаны некоторые факторы, влияющие на теплообмен излучением, а также будут реальные задачи на излучение.
К сожалению, данная страница уже перегружена, необходимо перейти к продолжению на: Следующую страницу.
Страница: 1 / Страница: 2
Все о дачном доме
Водоснабжение
Обучающий курс. Автоматическое водоснабжение своими руками. Для чайников.
Неисправности скважинной автоматической системы водоснабжения.
Водозаборные скважины
Ремонт скважины? Узнайте нужен ли он!
Где бурить скважину – снаружи или внутри?
В каких случаях очистка скважины не имеет смысла
Почему в скважинах застревают насосы и как это предотвратить
Прокладка трубопровода от скважины до дома
100% Защита насоса от сухого хода
Отопление
Обучающий курс. Водяной теплый пол своими руками. Для чайников.
Теплый водяной пол под ламинат
Обучающий Видеокурс: По ГИДРАВЛИЧЕСКИМ И ТЕПЛОВЫМ РАСЧЕТАМ
Водяное отопление
Виды отопления
Отопительные системы
Отопительное оборудование, отопительные батареи
Система теплых полов
Личная статья теплых полов
Принцип работы и схема работы теплого водяного пола
Проектирование и монтаж теплого пола
Водяной теплый пол своими руками
Основные материалы для теплого водяного пола
Технология монтажа водяного теплого пола
Система теплых полов
Шаг укладки и способы укладки теплого пола
Типы водных теплых полов
Все о теплоносителях
Антифриз или вода?
Виды теплоносителей (антифризов для отопления)
Антифриз для отопления
Как правильно разбавлять антифриз для системы отопления?
Обнаружение и последствия протечек теплоносителей
Как правильно выбрать отопительный котел
Тепловой насос
Особенности теплового насоса
Тепловой насос принцип работы
Запас мощности котла. Нужен ли он?
Про радиаторы отопления
Способы подключения радиаторов. Свойства и параметры.
Как рассчитать колличество секций радиатора?
Рассчет тепловой мощности и количество радиаторов
Виды радиаторов и их особенности
Автономное водоснабжение
Схема автономного водоснабжения
Устройство скважины Очистка скважины своими руками
Опыт сантехника
Подключение стиральной машины
Полезные материалы
Редуктор давления воды
Гидроаккумулятор. Принцип работы, назначение и настройка.
Автоматический клапан для выпуска воздуха
Балансировочный клапан
Перепускной клапан
Трехходовой клапан
Трехходовой клапан с сервоприводом ESBE
Терморегулятор на радиатор
Сервопривод коллекторный. Выбор и правила подключения.
Виды водяных фильтров. Как подобрать водяной фильтр для воды.
Обратный осмос
Фильтр грязевик
Обратный клапан
Предохранительный клапан
Смесительный узел. Принцип работы. Назначение и расчеты.
Расчет смесительного узла CombiMix
Гидрострелка. Принцип работы, назначение и расчеты.
Бойлер косвенного нагрева накопительный. Принцип работы.
Расчет пластинчатого теплообменника
Рекомендации по подбору ПТО при проектировании объектов теплоснабжения
О загрязнение теплообменников
Водонагреватель косвенного нагрева воды
Магнитный фильтр – защита от накипи
Инфракрасные обогреватели
Радиаторы. Свойства и виды отопительных приборов.
Виды труб и их свойства
Незаменимые инструменты сантехника
Интересные рассказы
Страшная сказка о черном монтажнике
Технологии очистки воды
Как выбрать фильтр для очистки воды
Поразмышляем о канализации
Очистные сооружения сельского дома
Советы сантехнику
Как оценить качество Вашей отопительной и водопроводной системы?
Профрекомендации
Как подобрать насос для скважины
Как правильно оборудовать скважину
Водопровод на огород
Как выбрать водонагреватель
Пример установки оборудования для скважины
Рекомендации по комплектации и монтажу погружных насосов
Какой тип гидроаккумулятора водоснабжения выбрать?
Круговорот воды в квартире
фановая труба
Удаление воздуха из системы отопления
Гидравлика и теплотехника
Введение
Что такое гидравлический расчет?
Невязка гидравлического расчета
Физические свойства жидкостей
Гидростатическое давление
Поговорим о сопротивлениях прохождении жидкости в трубах
Режимы движения жидкости (ламинарный и турбулентный)
Гидравлический расчет на потерю напора или как рассчитать потери давления в трубе
Местные гидравлические сопротивления
Профессиональный расчет диаметра трубы по формулам для водоснабжения
Как подобрать насос по техническим параметрам
Профессиональный расчет систем водяного отопления. Расчет теплопотерь водяного контура.
Гидравлические потери в гофрированной трубе
Теплотехника. Речь автора. Вступление
Процессы теплообмена
Тплопроводность материалов и потеря тепла через стену
Как мы теряем тепло обычным воздухом?
Законы теплового излучения. Лучистое тепло.
Законы теплового излучения. Страница 2.
Потеря тепла через окно
Факторы теплопотерь дома
Начни свое дело в сфере систем водоснабжения и отопления
Вопрос по расчету гидравлики
Конструктор водяного отопления
Диаметр трубопроводов, скорость течения и расход теплоносителя.
Вычисляем диаметр трубы для отопления
Расчет потерь тепла через радиатор
Мощность радиатора отопления
Расчет мощности радиаторов. Стандарты EN 442 и DIN 4704
Расчет теплопотерь через ограждающие конструкции
Найти теплопотери через чердак и узнать температуру на чердаке
Подбираем циркуляционный насос для отопления
Перенос тепловой энергии по трубам
Расчет гидравлического сопротивления в системе отопления
Распределение расхода и тепла по трубам. Абсолютные схемы.
Расчет сложной попутной системы отопления
Расчет отопления. Популярный миф
Расчет отопления одной ветки по длине и КМС
Расчет отопления. Подбор насоса и диаметров
Расчет отопления. Двухтрубная тупиковая
Расчет отопления. Однотрубная последовательная
Расчет отопления. Двухтрубная попутная
Расчет естественной циркуляции. Гравитационный напор
Расчет гидравлического удара
Сколько выделяется тепла трубами?
Собираем котельную от А до Я…
Система отопления расчет
Онлайн калькулятор Программа расчет Теплопотерь помещения
Гидравлический расчет трубопроводов
История и возможности программы – введение
Как в программе сделать расчет одной ветки
Расчет угла КМС отвода
Расчет КМС систем отопления и водоснабжения
Разветвление трубопровода – расчет
Как в программе рассчитать однотрубную систему отопления
Как в программе рассчитать двухтрубную систему отопления
Как в программе рассчитать расход радиатора в системе отопления
Перерасчет мощности радиаторов
Как в программе рассчитать двухтрубную попутную систему отопления. Петля Тихельмана
Расчет гидравлического разделителя (гидрострелка) в программе
Расчет комбинированной цепи систем отопления и водоснабжения
Расчет теплопотерь через ограждающие конструкции
Гидравлические потери в гофрированной трубе
Гидравлический расчет в трехмерном пространстве
Интерфейс и управление в программе
Три закона/фактора по подбору диаметров и насосов
Расчет водоснабжения с самовсасывающим насосом
Расчет диаметров от центрального водоснабжения
Расчет водоснабжения частного дома
Расчет гидрострелки и коллектора
Расчет Гидрострелки со множеством соединений
Расчет двух котлов в системе отопления
Расчет однотрубной системы отопления
Расчет двухтрубной системы отопления
Расчет петли Тихельмана
Расчет двухтрубной лучевой разводки
Расчет двухтрубной вертикальной системы отопления
Расчет однотрубной вертикальной системы отопления
Расчет теплого водяного пола и смесительных узлов
Рециркуляция горячего водоснабжения
Балансировочная настройка радиаторов
Расчет отопления с естественной циркуляцией
Лучевая разводка системы отопления
Петля Тихельмана – двухтрубная попутная
Гидравлический расчет двух котлов с гидрострелкой
Система отопления (не Стандарт) – Другая схема обвязки
Гидравлический расчет многопатрубковых гидрострелок
Радиаторная смешенная система отопления – попутная с тупиков
Терморегуляция систем отопления
Разветвление трубопровода – расчет
Гидравлический расчет по разветвлению трубопровода
Расчет насоса для водоснабжения
Расчет контуров теплого водяного пола
Гидравлический расчет отопления. Однотрубная система
Гидравлический расчет отопления. Двухтрубная тупиковая
Бюджетный вариант однотрубной системы отопления частного дома
Расчет дроссельной шайбы
Что такое КМС?
Расчет гравитационной системы отопления
Конструктор технических проблем
Удлинение трубы
Требования СНиП ГОСТы
Требования к котельному помещению
Вопрос слесарю-сантехнику
Полезные ссылки сантехнику
—
Сантехник – ОТВЕЧАЕТ!!!
Жилищно коммунальные проблемы
Монтажные работы: Проекты, схемы, чертежи, фото, описание.
Если надоело читать, можно посмотреть полезный видео сборник по системам водоснабжения и отопления
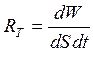
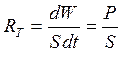 ,
,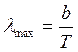 ;
;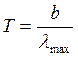 ;
; 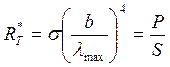 .
. м.
м.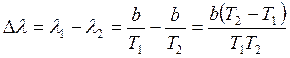 .
.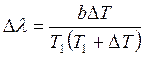 .
.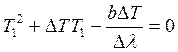 ;
; ;
; ;
;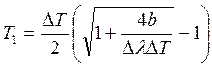 .
.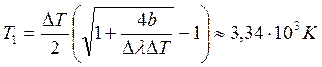 .
.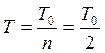
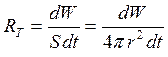 ,
,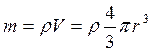 −
−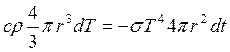 ;
;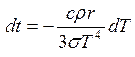 .
.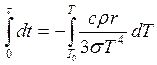 ;
;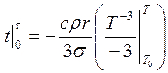 ;
;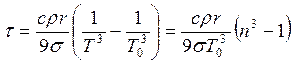 .
.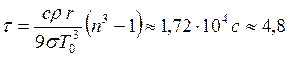 ч.
ч.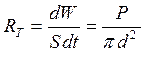 ,
,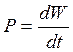 − мощность излучения,
− мощность излучения,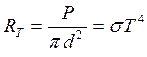 .
.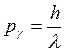 .
.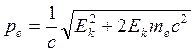 или
или 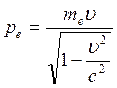 .
.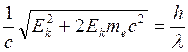 ;
;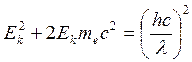 .
.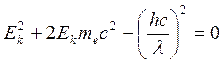 ;
;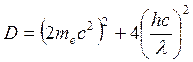 ;
;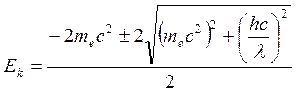 .
.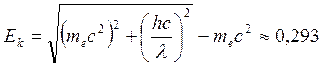 МэВ
МэВ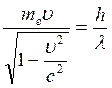 ;
;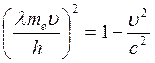 ;
;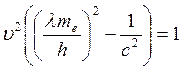 ;
;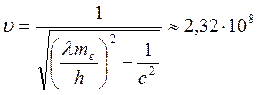 м/с.
м/с.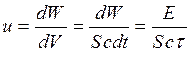 − объемная плотность
− объемная плотность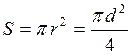 − площадь светового пятна;
− площадь светового пятна; 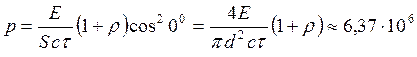 Па.
Па.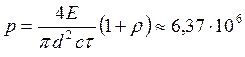 Па.
Па.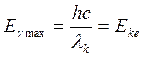 ;
;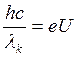 .
.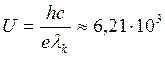 В;
В;
