Привет, ребята!
Вы знаете, я хотела узнать площадь
нашей страны, но мне это не сразу удалось сделать. Дело в том, что её границы
имеют неправильную форму – это не прямоугольник, не квадрат, и даже не круг.
Я обратилась за помощью к нашей царице, и она
рассказала мне, как находить площадь любой, самой искривлённой фигуры. Царица
дала мне вот такое простое приспособление. Это прозрачная пластина или плёнка с
разлиновкой в клеточку. Называется она – палетка. В
зависимости от размера фигуры, площадь которой надо узнать, палетка может быть
разделена на квадратные миллиметры, квадратные сантиметры или квадратные
дециметры.
Представьте
себе, что надо узнать площадь вот такой фигуры.
Накладываем
на неё палетку.
Сначала
считаем, сколько всего целых квадратиков. Их тридцать четыре. Теперь считаем
все оставшиеся кусочки. Их восемь. Люди договорились, что каждые два
кусочка засчитывают за один полный квадратик. Поэтому количество кусочков
делим на два. Получилось четыре.
Складываем
тридцать четыре и четыре. Это тридцать восемь. Значит, площадь этой фигуры – примерно
тридцать восемь квадратиков.
Так
как в школе чаще всего пользуются палетками, разделёнными на квадратные
сантиметры, то вы бы сказали, что площадь данной фигуры примерно равна тридцати
восьми квадратным сантиметрам. Почему примерно? Потому что площадь фигуры по
палетке вряд ли возможно определить абсолютно точно, ведь редко два кусочка
могут идеально заменить целый квадратик.
А
теперь попробуем найти площадь вот такой, совершенно бесформенной фигуры.
Опять
накладываем на неё палетку. Считаем целые квадратики.
Их
семнадцать. Теперь считаем кусочки. Их двадцать четыре. Количество кусочков
делим на два и полученное число прибавляем к семнадцати. Получилось примерно
двадцать девять квадратных сантиметров.
Иногда
случается и так, что количество кусочков – нечётное число,
например, тринадцать или двадцать пять. Тогда делим на два ближайшее чётное
число, больше данного на один. Ведь всё равно при помощи палетки точно площадь
фигуры измерить невозможно. А вот почему берём чётное число больше данного, вы
узнаете в пятом классе.
Запомнили,
ребята, как мы определяем площадь фигур с помощью палетки?
̶ Накладываем
палетку на фигуру.
̶ Считаем
количество целых квадратов.
̶ Считаем
количество кусочков.
̶ Количество
кусочков делим на два…
̶ Складываем
полученное число с количеством целых квадратов….
̶ Записываем
ответ.
Видите,
всё просто!
Кстати,
именно так, используя план местности и палетку, можно найти площадь участка
земли, или озера, или целого города, и даже страны. Вот этим я сейчас и
займусь. Пока, ребята!
Оборудование. Учебник Э.И.Александровой
(изд-во ВИТА-ПРЕСС), на каждого ученика листочки
четырёх цветов, листочки с четырьмя вариантами
заданий, непрозрачные конверты с палетками из
целлофана, два больших демонстрационных листа с
рисунками 2 и 3, 6 листов для работы (по количеству
групп) с фигурой на рисунке 2, 12 листов с фигурой
на рисунке 3.
Тема. Измерение площадей криволинейных
фигур. Палетка.
Цели.
Образовательная: познакомить с способом
измерения площадей криволинейных фигур; с
устройством для измерения площадей – палеткой;
закреплять умение находить площади
прямолинейных фигур.
Развивающая: развивать внимание,
наблюдательность, умение рассуждать, обобщать и
делать выводы.
Воспитательная: воспитывать умение общаться,
аккуратность, внимательность.
1. Учебная ситуация успеха
Учитель. Чем мы занимались на вчерашнем уроке?
Ученики. Находили площади и периметры фигур.
Учитель. Как найти площадь геометрической
фигуры?
Ученики. Площадь прямоугольника и треугольника
находят по формуле. Если это не прямоугольник и
не треугольник, то сначала многоугольник надо
разбить или достроить до фигур, площади которых
мы уже знаем как находить.
Учитель. Я предлагаю вам выполнить эти задания.
Здесь 4 варианта заданий. Посмотрите на них и
выберите себе любое. Все 4 варианта лежат у вас на
партах.
На доске четыре варианта заданий. Каждое
записано своим цветом. У детей на партах кроме
карточек с фигурами четырёх цветов, квадраты
соответствующих цветов.
На доске

Дети, решив задание, поднимают карточку с
соответствующим заданию цветом. По цвету они
находят группу, сверяют решение, выбирают одного
представителя от группы, который записывает
решение на доске. Остальные сверяют свои ответы с
доской.
Учитель. Ребята, научились мы находить площади
геометрических фигур?
Ученики. Да.
2. Постановка учебной задачи
Учитель. А теперь найдите площадь этой фигуры.
Показывает и вывешивает на доску
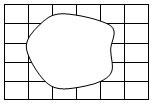
Ученики молчат.
Учитель. Почему вы не можете выполнить задание?
Ученики. Это не прямоугольник и не треугольник.
Это не многоугольник.
Учитель. Чем эта фигура отличаются от нам
известных фигур, многоугольников?
Ученики. Непонятно, где длина, ширина. Нет углов.
Фигуры некрасивые, какие-то кривые.
Учитель. Да, все многоугольники состоят из
прямых линий. Поэтому их называют прямолинейными
фигурами. А из каких линий состоят эти фигуры?
Как бы вы их назвали?
Ученики. Кривые.
Учитель. В математике такие фигуры называют криволинейными.
Учитель. Чем же мы будем заниматься сегодня на
уроке?
Ученики. Учиться находить площади
криволинейных фигур.
Учитель фиксирует проблему на доске:
S = ?
3. Поиск решения поставленной задачи
Учитель. Как же мы будем решать эту задачу? Как
вы находили площадь прямоугольника, когда ещё не
знали формулу его площади?
Ученики. Мы измеряли площадь прямоугольника с
помощью мерки.
Учитель. А для криволинейной фигуры такой
способ можно попробовать?
Ученики. Да.
Учитель. Как можно узнать площадь
криволинейной фигуры с помощью мерки в одну
клетку?
Ученики. Разбить на мерки, продолжив линии
клеток-мерок.
Учитель. Что будете делать, когда разобьёте
фигуру на мерки, чтобы узнать площадь фигуры?
Ученики. Посчитаем количество мерок в фигуре.
Учитель. Работаем в группах.
Представители от групп записывают свои ответы
на доске. Ответы оказываются разными.
Учитель. Почему ответы оказались разными? Наши
ребята не умеют считать?
Группа, у которой количество мерок меньше,
объясняют: “Мы не считали нецелые мерки”.
Учитель. Правильно будет вообще не считать
неполные мерки?
Ученики. Нет.
Учитель. А считать половинку как полную
мерку-квадрат можно?
Ученики. Нет.
Учитель. Что же делать с неполными мерками,
ребята? Как их считать?
Ученики. Складывать по две мерки.
Учитель. Да, в математике договорились считать
всё количество неполных мерок и делить на 2.
Учитель. Посчитайте ещё раз количество полных
мерок. Неполных мерок.
Ученики работают в группах.
Учитель. Скольким квадратным меркам равна
площадь фигуры?
Представители от групп называют ответы. Все
сверяют со своими ответами.
4. Моделирование
Учитель. Что мы сейчас нашли?
Ученики. Мы узнали площадь криволинейной
фигуры.
Учитель. Давайте вспомним, как мы это делали.
Дети говорят, учитель записывает на доске.
1. Разбить на мерки.
1. Посчитать полные мерки.
2. Посчитать неполные мерки и разделить на 2.
3. Сложить.
Учитель. Так можно найти площадь только этой
криволинейной фигуры?
Ученики. Можно найти площадь и другой фигуры.
Учитель. Как записать, чтобы было понятно, что
таким способом можно воспользоваться для
вычисления площади любой криволинейной фигуры?
Как обозначить полные мерки? Неполные мерки?
Дети предлагают разные варианты. Учитель
сообщает, что в математике договорились полные
мерки обозначать буквой n, а неполные мерки
буквой m.
Учитель. Кто закончит запись So = ?
На доске появляется запись: So = n + m : 2
Физминутка
5. Рефлексия
Учитель. Откройте учебники на стр. 61. Найдите №
88. Работая в парах, узнайте площади криволинейных
фигур: 1 ряд – площадь первой фигуры, 2 ряд –
площадь второй фигуры, 3 ряд – площадь третьей
фигуры.
Проверка
Представители от пар, выполнивших задание
первыми, записывают на доске ответы. Остальные
сравнивают свои ответы с их записями.
Учитель. По какой формуле вы находили площадь
криволинейной фигуры?
Ученики. S = n + m : 2
Учитель. При таком способе нахождения площади
(путём разбиения фигуры на мерки-квадраты)
измерения получаются неточными.
Какие единицы измерения площадей вы знаете?
Ученики. Кв.см, кв.мм, кв.м, кв.км.
Учитель. Откройте учебник на с. 62 , № 89.
Одну и ту же фигуру измеряли сначала в кв.см,
потом в кв. мм
Как вы думаете, в каком случае измерения
выполнены более точно: в кв. см или в кв.мм?
Ученики. Более точно измерили квадратными мм .
6. Конкретизация способа нахождения площади
криволинейной фигуры
Учитель. Мы научились измерять площади
криволинейных фигур, разбивая их на клетки –
мерки.
А сейчас посмотрите вот на эту фигуру:
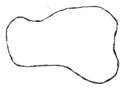
Надо узнать площадь этой фигуры с помощью мерки
в 1 кв. см.
Чем отличается данное задание от предыдущего?
Ученики. Нет клеточек, по которым можно
провести линии мерок.
Учитель. Да, здесь нет сетки из квадратов. Как же
узнать, сколько полных и неполных кв. см
поместилось в данной фигуре?
Все задумались и молчат. Один ученик предлагает
свою версию – накинуть сверху какую-нибудь сетку
из квадратиков.
Учитель. Да, можно изготовить специальное
устройство (показываю). Это палетка.
Достаньте из конверта палетку. Кто догадался,
как её сделали?
Ученики. Расчертили на квадраты со стороной в 1
см.
Учитель. А как ей пользоваться?
Ученики. Наложить на фигуру и посчитать
количество клеток.
Посчитайте в парах площадь этой криволинейной
фигуры.
Учитель. Выполните задание в учебнике №
90.Каждый самостоятельно.
Проверка.
Три первых ученика, выполнивших задание,
выходят к доске и записывают свои ответы
Класс сверяет ответы.
7. Дз.
Учитель. Дома вам надо найти площади фигур из №
91. Что вам для этого понадобится?
Ученики. Палетка.
Учитель. Кто сможет сделать её сам?
Как это сделать?
Думаю, что все справятся с этой работой.
Если вы увидите фигуру, площадь которой можно
найти другим способом, то вычислите площадь
такой фигуры двумя способами: с помощью палетки и
без неё.
8. Итоговая рефлексия
Учитель. Какую задачу решали на уроке?
Ученики. Учились находить площадь
криволинейной фигуры.
Учитель. Кто сможет дома рассказать родителям
,как найти площадь криволинейной фигуры?
Как это сделать?
Учитель. А как вы думаете, чем мы будем
заниматься на следующих уроках?
Ученики. Будем решать задачи на нахождение
площадей фигур.
Будем находить новые формулы для нахождения
площадей фигур.
Учитель. Да, на следующих уроках мы будем
использовать полученные знания в решении задач.
|
Площадь фигуры (треугольник, четырёхугольник, трапеция и др.) по клеточкам (клеткам). Какие есть формулы?
Есть способ, при котором надо воспользоваться формулой, основой которой будет понятие узла, узла внутреннего и узла внешнего. Узел это пересечение линий, образующих эти самые клеточки. Внешние узлы, это узлы, находящиеся на сторонах и вершинах геометрических фигур, площади которых нам надо найти. А внутренние узлы, это узлы внутри этих фигур. Клеточки у нас со сторонами равными одному сантиметру (1 см). Формула, о которой идет речь, называется формула Пика. Выглядит она вот так:
И по ней очень просто посчитать площадь фигуры S. В этой формуле M это количество внешних узлов, N – количество внутренних узлов. Приведем пример, возьмем геометрическую фигуру параллелограмм:
Внутренние узлы – синие – N – их у нас 20. Внешние узлы – красные – М – их у нас 18 и их количество нам надо поделить на два, получится 18/2 = 9 узлов. Складываем 9 + 20 и вычитаем единицу: 20 + 9 – 1 = 28 см². Еще один пример:
S = 14/2 + 43 – 1 = 49 см². система выбрала этот ответ лучшим
Ксарфакс 6 лет назад Допустим, у нас есть произвольная фигура, построенная на листе в клетку. Необходимо вычислить её площадь. Площадь фигуры по клеточкам Для того, чтобы найти площадь любой фигуры по клеточкам, можно использовать формулу Пика. Данная формула основана на подсчёте количества узлов, лежащих внутри фигуры и на её границе. Узел – это точка, которая лежит на пересечении 2 линий данной сетки: вертикальных и горизонтальных. Площадь фигуры по клеточкам находится по формуле:
N – количество узлов, которые находятся внутри фигуры. M – количество узлов, которые находятся на границах (на вершинах и сторонах). Примеры нахождения площади по клеточкам 1) Найдём площадь треугольника. Будем считать, что одна клетка – это 1 см. Отметим внутренние узлы и узлы, которые находятся на границах.
N = 7 (внутренние). M = 8 (узлы на границах). Площадь треугольника S = 7 + 8/2 – 1 = 10 см². 2) Найдём площадь трапеции по клеточкам, одна клетка – это 1 см. Отметим все узлы и подсчитаем их количество.
N = 11 (внутренние). M = 12 (узлы на границах). Площадь трапеции S = 11 + 12/2 – 1 = 16 см². 3) Найдём площадь произвольного многоугольника. Одна клетка – это 1 см. Отметим внутренние узлы и узлы, расположенные на границах фигуры. Подсчитаем их количество.
N = 6 (внутренние узлы). M = 8 (узлы на границах). Площадь многоугольника S = 6 + 10/2 – 1 = 10 см².
Марина Вологда 3 года назад Такие задачи очень часто встречаются, когда известен размер клеточки и дана фигура. Вот пример таких задач:
Решение зависит от того, какая фигура дана и как именно она размещена относительно клеточек. Возьмем простой пример, необходимо вычислить площадь вот такого треугольника:
Вспоминаем правило: Теперь считаем, сколько клеточек треугольник в длину и сколько в высоту. У нас получается 2 в высоту и 6 в длину. Подставляем к формуле: S = 1/2 х 2 х 6 = 6 см2. Считаем по клеточкам, подставляя формулу Пика:
Целых клеточек у нас 3. Теперь считаем, сколько не целых: 6. Делим их на 2. S = 3 + 6:2 = 6 см2. А теперь высчитываем по формуле Пика: количество узлов сетки внутри – 2, количество узлов сетки, лежащих на границах – 10. Подставляем к формуле и получаем – 2 + 10:2 – 1 = 6 см2. Теперь давайте рассмотрим вот такой треугольник:
Чтобы найти площадь, вспоминаем правило: Считаем клеточки и подставляем в формулу: S = 1/2 х 2 х 6 = 6 см2. А теперь находим по клеточкам: целых клеточек 2, не целых клеточек 8. Подставляем в формулу: 2 + 8:2 = 6 см2. Пробуем сделать по формуле Пика: количество узлов сетки внутри – 3, количество узлов сетки, лежащих на границах – 8. Подставляем к формуле и получаем – 3 + 8:2 – 1 = 6 см2.
Enot-Nina 3 года назад Найти площадь геометрической фигуры можно самыми разными способами: Самый простой вариант – это вручную посчитать клеточки – целые и половинки также поскладывать. Простой, хотя и не самый быстрый и может не самый точный способ, но он работает. Чтобы легче было считать, достаточно расчертить фигуру на более простые. Есть еще один способ – это использовать давно разработанную формулу. Это так называемая формула Пика. Для нее нужно посчитать количество узлов – точек пересечения клеточек, что окружены фигурой (находятся внутри нее), а также подсчитать количество пограничных узлов – по контуру фигуры. Вот на картинке наглядно показано, как ее можно применять, чтоб посчитать площадь любой фигуры по клеточкам:
Бархатные лапки 3 года назад Площадь любого многоугольника можно посчитать по клеточкам. Для этого применяем формулу Пика. На нашем рисунке В – количество узловых клеточек внутри фигуры, Г – количество узлов на границе . Узлы – пересечение двух линий. многоугольника. Площадь равна S = В + Г/2 – 1 Считаем точки на рисунке и подставляем в формулу. – 10 + 7/2 -1 = 12,5. Таким образом можно посчитать площадь, если вершины фигуры лежат в узлах.
Ann Luka 6 лет назад Чтобы найти площадь фигуры по клеточкам, нужно посчитать сколько в фигуре целых клеточек. Потом нужно посчитать сколько не целых и поделить их количество на 2. Добавить к получившемуся числу количество целых клеточек – это и будет правильный ответ. Например. В треугольнике 3 целых клетки и 4 не целых. 3+4/2=5 пощадь треугольника 5 клеток.
Outline 3 года назад Для того, чтобы определить площадь фигуры на бумаге в клеточку есть универсальная формула Пика, позволяющая вычислить площадь изображения, но в только в том случае, если вершины искомой фигуры имеют целые (натуральные числа) координаты. Называется эта формула, в честь Георга Пика: S=В + Г / 2 − 1 В этой формуле буквенные обозначения означают следующее: В — количество целочисленных точек внутри многоугольника; Г — количество целочисленных точек на границе (вершинах и сторонах) многоугольника; S – площадь фигуры. Здесь используется понятие “целочисленные” – это те, точки, которые расположены на пересечениях сетки (в ее узлах). Для примера, найдем площадь треугольника:
Обозначим внутренние точки нашей фигуры красными кружками, а те, что на границах – синим цветом. Считаем красные и синие точки: В=12, Г=4. Исходя из подсчетов определяем площадь треугольника по формуле: S=В+Г/2-1=12+2-1=13. Можно убедиться в правильность проведенных выше расчетах. Рассчитываем площадь квадрата, обведенного красным, и вычитаем площади зеленого, синего и фиолетового треугольников:
S квадрата равна 36, площади треугольников: синего – 6, зеленого – 2, фиолетового – 15. Исходя из полученных данных, S белого треугольника равна 13: S=36-6-15-2=13.
KritikSPb 3 года назад Подсчет клеточек – дело полезное. С их помощью можно найти площадь геометрической фигуры. Достаточно воспользоваться формулой, доказанной Георгом Пиком в 1899 году. Подходит для расчета площади фигур с прямыми сторонами и целым количеством углов, чаще всего применяют для нахождения площади разносторонних треугольников и многоугольников с числом углов больше 4-х. На теорему Пика есть задания в ЕГЭ.
127771 3 года назад Сначала я подумал, что нужно будет фигуру, которая указана на рисунке в клеточку разбить по фигурам так, чтобы можно посчитать площадь каждой фигуры по-отдельности, но оказалось все намного проще. Существует для данной задачи специальная формула Пика, которая выглядит следующим образом: Площадь = В + Г/2 – 1, где:
Теперь разберемся на примере, у нас есть такой пример:
Перед нами трапеция. Допустим площадь одной клетки 1 кв.см. Теперь можно воспользоваться формулой: 11+12/2-1=16 кв.см.
Бекки Шарп 3 года назад Найти площадь фигуры можно если вершины фигуры находятся в уголках клеточек, так называемые Целочисленные вершины или узловые точки. Решать задачу будем по формуле Пика, где
Вот такая фигура у нас –
Считаем точки и подставляем в формулу: S = 17 + 14/2 – 1 = 23 Ответ мы получаем в квадратных единицах, то есть клеточках. Знаете ответ? |
Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.
Площади равных фигур равны. Их периметры тоже равны.
Площадь квадрата
Запомните!
![]()
Для вычисления площади квадрата нужно умножить его длину на саму себя.
S = a · a
Пример:

SEKFM = EK · EK
SEKFM = 3 · 3 = 9 см2
Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:
S = a2
Площадь прямоугольника
Запомните!
![]()
Для вычисления площади прямоугольника нужно умножить его длину на ширину.
S = a · b
Пример:

SABCD = AB · BC
SABCD = 3 · 7 = 21 см2
Запомните!
![]()
Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.
Площадь сложных фигур
Запомните!
![]()
Площадь всей фигуры равна сумме площадей её частей.
Задача: найти площадь огородного участка.

Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.
Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

SABCE = AB · BC
SEFKL = 10 · 3 = 30 м2
SCDEF = FC · CD
SCDEF = 7 · 5 = 35 м2
Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = SABCE + SEFKL
S = 30 + 35 = 65 м2
Ответ: S = 65 м2 — площадь огородного участка.
Свойство ниже может вам пригодиться при решении задач на площадь.
Запомните!
![]()
Диагональ прямоугольника делит прямоугольник на два равных треугольника.
Площадь любого из этих треугольников равна половине площади прямоугольника.
Рассмотрим прямоугольник:

АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников

ABC и
 ACD
ACD
Вначале найдём площадь прямоугольника по формуле.
SABCD = AB · BC
SABCD = 5 · 4 = 20 см2
S
ABC = SABCD : 2
S
ABC = 20 : 2 = 10 см2
S
ABC =
S
ACD = 10 см2
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
3 декабря 2015 в 22:54
Ирина Петренко

Профиль
Благодарили: 0
Сообщений: 1

Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
как написать правильно площадь треугольника?![]()
0
Спасибо
Ответить
9 декабря 2015 в 19:41
Ответ для Ирина Петренко
Тима Клюев

Профиль
Благодарили: 0
Сообщений: 8

Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
S(рисуешь мини треугольник) = ,,,,,
0
Спасибо
Ответить
Практическая работа.
а) Вырежь из клетчатой бумаги прямоугольник со сторонами 3 см и 4 см. Чему равна его площадь в квадратных сантиметрах? В клеточках?
б) Нарисуй на вырезанном прямоугольнике замкнутую кривую линию A. Можешь ли ты точно указать площадь фигуры A, выраженную в клеточках?
Между какими числами заключена эта площадь?

reshalka.com
ГДЗ учебник по математике 4 класс Петерсон. 17 урок. Оценка площади. Номер №2
Решение а
Вырежем прямоугольник:

Найдем площадь прямоугольника в
с
м
2
:
S
к
в
.
с
м
=
3
∗
4
=
12
с
м
2
.
Найдем площадь прямоугольника в клеточках:
8 клеточек в длину;
6 клеточек в ширину;
S
к
л
е
т
о
ч
к
а
х
=
8
∗
6
=
48
клеточек.
Решение б
Нарисуем замкнутую кривую линию A:

Точно указать площадь фигуры A невозможно, но она заключена между числами:
4 < S < 18





















