Напротив ворот находятся гараж. Он обозначен цифрой 2. За гаражом располагается жилой дом 1.
Большой газон отмечен цифрой 5. На газоне располагаются: 2 клумбы – 6 (ромбы), бассейн 3 и беседка 4.
Получается ответ: 1236.
Клумбы имеют форму ромбов.
Площадь ромба легко узнать по диагоналям. Она равна половине их произведения.
Одна клетка равна одному метру.
Получается,
S = 2*4*1/2=4 м^2.
Беседка и бассейн имеют форму круга.
Площадь круга равна произведению числа «пи» на радиус в квадрате.
Площадь беседки равна
S беседки = 2^2П=4П м^2.
Площадь бассейна равна
S бассейна = 3^2П=9П м^2.
Площадь бассейна больше площади беседки в 9П/4П = 2,25 раза.
Из площади территории, который будет занимать газон, необходимо вычесть площадь беседки и бассейна, ведь они не будут засеваться.
12*24-3,14*3^2-3,14*2^2= 247,18.
Для варианта А необходимо 247,18/63=3,92. Округляем в большую сторону – 4. Для засева всей площади потребуется 4*500=2000 рублей.
Вариант Б: 247,18/40=6,18. Округляем в большую сторону – 7. Рассчитываем стоимость: 7*330=2310 рублей.
Вариант В: 247,18/45=5,5. Округляем до 6. Стоимость: 6*340= 2040 рублей.
Вариант Г: 247,18/35 = 7,06. Округляем до 8. Затраченные деньги: 8*290= 2320 рублей.
Наиболее выгодная стоимость у первого варианта.
Версия для печати и копирования в MS Word
Найдите площадь, которую занимает одна клумба. Ответ дайте в квадратных метрах.
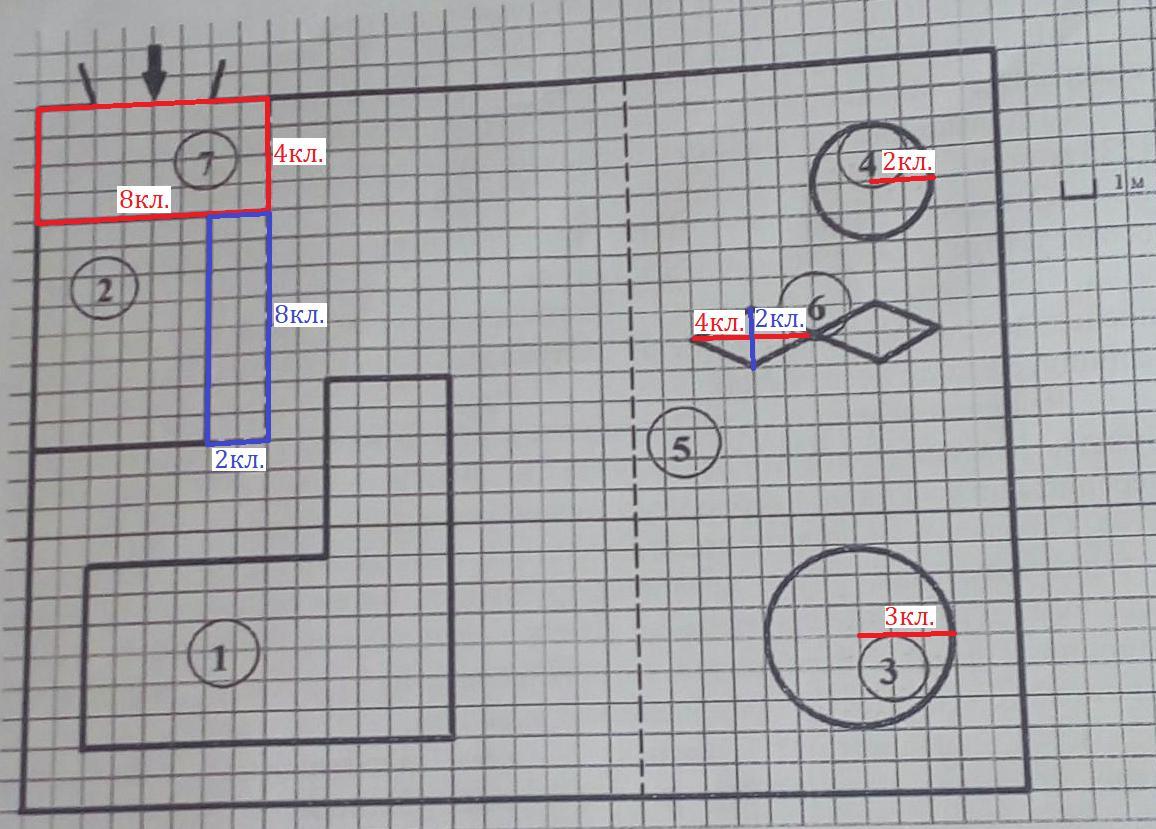
На плане изображено домохозяйство по адресу с. Сергеево, 8-й Кленовый пер, д. 1 (сторона каждой клетки на плане равна 1 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота. При входе на участок напротив ворот находится гараж, а за гаражом — жилой дом. Площадь, занятая гаражом, равна 48 кв. м. Слева от ворот находится большой газон, отмеченный на плане цифрой 5. На газоне имеются круглый бассейн, беседка и две ромбовидные клумбы. Беседка отмечена на плане цифрой 4. При въезде на участок имеется площадка, вымощенная тротуарной плиткой размером 0,2 м × 0,1 м и обозначенная на плане цифрой 7.
Спрятать решение
Решение.
Площадь, которую занимает одна клумба, равна:
м2.
Ответ: 4.
1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | жилой дом | гараж | бассейн | клумбы |
|---|---|---|---|---|
| Цифры |
2
Тротуарная плитка продаётся в упаковках по 45 штук. Сколько упаковок плитки понадобилось, чтобы выложить площадку перед гаражом?
3
Во сколько раз площадь бассейна больше площади беседки?
4
Хозяин участка хочет обновить газон к новому дачному сезону. Для этого он планирует купить семена газонной травы у одного из поставщиков. Цена одной упаковки семян, её масса и рекомендуемый расход указаны в таблице.
| Поставщик | Цена 1 уп. семян (руб.) |
Масса 1 уп. семян (кг) |
Рекомендуемый расход 1 уп. семян (кв. м.) |
|---|---|---|---|
| А | 500 | 1,8 | 63 |
| Б | 330 | 1 | 40 |
| В | 340 | 1 | 45 |
| Г | 290 | 1 | 35 |
Территорию, занятую бассейном и беседкой, засевать не предполагается. Клумбы планируется убрать и на их месте тоже засеять газонную траву. Число π возьмите равным 3. Во сколько рублей обойдётся наиболее дешёвый вариант?
ledsmarcing771
Вопрос по алгебре:
Клумба прямоугольной формы окружена дорожкой, ширина которой 1м.Площадь дорожки 26квадратных метров.Найдите стороны клумбы, если одна из них на 5 метров больше другой
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
cemavengh
Пусть длина наименьшей стороны клумбы х м, так как вторая сторона длиннее на 5м, то ее длина составит (х+5)м. Вокруг клумбы идет дорожка шириной 1 м, значит длина стороны дорожки составит(1+х+5+1)=(х+7)м — широкая сторона, и меньшая сторона составит (1+х+1)м=(х+2)м. Площадь дорожки составляет 26кв.м. и складывается из площади 4-ч прямоугольников, из которых стороны двух длинных прямоугольников равны по (х+7)м и 1м. Площадь этих прямоугольников равна и составляет S1.2=1*(х+7)м=(х+7)м, и 2 прямоугольника со сторонами 1м и (х+2)м, и площади их равны 1*(х+2)м= (х+2)м. Вся площадь дорожки составит 2*(х+7)+2*(х+2)=26. Делим обе части уравнения на 2, получаем(х+7)+(х+2)=132х+9=132х=13-92х=4х=2Таким образом наименьшая сторона клумбы равна 2м, тогда наибольшая 2+5=7м
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат — это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Алгебра.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи —
смело задавайте вопросы!
Для начала определим, какими цифрами обозначены на участке разные строения.
Слева от ворот находится сарай, обозначен цифрой 2.
Справа — гараж, зашифрован под цифрой 1.
Жилой дом самый большой по площади, обозначен цифрой 3.
Огород отмечен пятеркой.
Под цифрой 4 спрятана теплица.
Получается на второй вопрос в ответе необходимо указать цифровую комбинацию — 3412.
Клумбы на участке круглые. Площадь круга определяется по формуле.
S=П(R^2).
Радиус первой клумбы 2 метра.
Площадь равна
S1=3,14*2^2=12,56 м2.
Радиус второй клумбы 3 метра.
Площадь второй
S1=3,14*3^2=28,26 м2.
Общая площадь двух клумб.
S0=12,56+28,26=40,82 м2.
Площадь жилого дома.
8*8+4*2=72 м2.
Посчитаем, сколько плитки необходимо для выкладки извилистых дорожек до дома и огорода. По рисунку их 40.
Вычислим площадь дорожки от гаража до сарая.
16*4=64 м2.
В 1 большой клетке помещается 4 плитки.
64*4=256 плиток.
Общее число необходимой плитки.
256+40=296.
В одной упаковке 5 плиток.
296/5=59,2.
Одну плитку нельзя докупить отдельно, поэтому необходимо купить на 1 упаковку больше. Получается необходимо купить 60 упаковок плитки.
![]()
Вычислите примерно площадь, которую занимают две клумбы вместе. Число π возьмите равным 3,14. Ответ запишите в квадратных метрах.
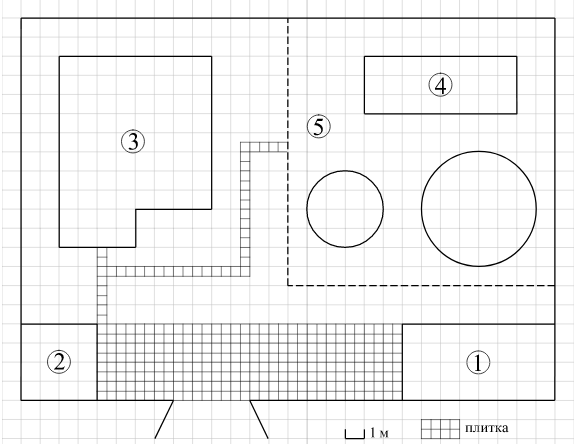
На плане изображено домохозяйство по адресу с. Кондратьево, 2-й Прудовой пер, д. 7 (сторона каждой клетки на плане равна 1 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляется через единственные ворота.
При входе на участок слева от ворот находится сарай, а справа гараж. Площадь, занятая сараем, равна 16 кв. м. Жилой дом находится в глубине территории. Помимо гаража, жилого дома и сарая, на участке имеются теплица и две круглые клумбы, расположенные на территории огорода (огород отмечен на плане цифрой 5). Все дорожки внутри участка имеют ширину 0,5 м и вымощены тротуарной плиткой размером 0,5 м × 0,5 м. Между сараем и гаражом имеется площадка, вымощенная той же плиткой.
<hr />
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
<hr />
Найдите площадь, которую занимает жилой дом. Ответ дайте в квадратных метрах.
<hr />
Тротуарная плитка продаётся в упаковках по 5 штук. Сколько упаковок плитки понадобилось, чтобы выложить все дорожки и площадку перед гаражом?
1 ответ:
![]()
2
0
Для начала определим, какими цифрами обозначены на участке разные строения.
Слева от ворот находится сарай, обозначен цифрой 2.
Справа — гараж, зашифрован под цифрой 1.
Жилой дом самый большой по площади, обозначен цифрой 3.
Огород отмечен пятеркой.
Под цифрой 4 спрятана теплица.
Получается на второй вопрос в ответе необходимо указать цифровую комбинацию — 3412.
Клумбы на участке круглые. Площадь круга определяется по формуле.
S=П(R^2).
Радиус первой клумбы 2 метра.
Площадь равна
S1=3,14*2^2=12,56 м2.
Радиус второй клумбы 3 метра.
Площадь второй
S1=3,14*3^2=28,26 м2.
Общая площадь двух клумб.
S0=12,56+28,26=40,82 м2.
Площадь жилого дома.
8*8+4*2=72 м2.
Посчитаем, сколько плитки необходимо для выкладки извилистых дорожек до дома и огорода. По рисунку их 40.
Вычислим площадь дорожки от гаража до сарая.
16*4=64 м2.
В 1 большой клетке помещается 4 плитки.
64*4=256 плиток.
Общее число необходимой плитки.
256+40=296.
В одной упаковке 5 плиток.
296/5=59,2.
Одну плитку нельзя докупить отдельно, поэтому необходимо купить на 1 упаковку больше. Получается необходимо купить 60 упаковок плитки.
Читайте также
![]()
Задача решаемая, и я решил!)
Приступим!
z^2>=0, так как квадрат числа всегда положительный, или равен 0.
xy-z^2=1 — отсюда следует, что xy>=1
xy>=1 отсюда следует что либо x и y либо оба положительны, либо оба отрицательны, но по скольку мы знаем что x+y=2 следует, что и x и y положительные числа, так как из суммы отрицательных чисел, положительное число 2 никак не получиться. У нас появилась новая система уравнений, неравенств. — xy>=1; x+y=2; x>0; y>0, z пока оставим в покое. Отбросим пока x>0; y>0, и решим систему уравнений, неравенств — xy>=1; x+y=2. xy>=1 это тоже самое что y>=1/x, отсюда можно сделать функцию y=1/x — график данной функции — стандартная гипербола. А x+y=2 это тоже самое что y=2-x -стандартная линейная функция поднятая на 2 единицы вверх и перевернутая. Я Сделал себе рисунок этих графиков, что бы понять, что они пересекаются всего в 1й или 2х точках.
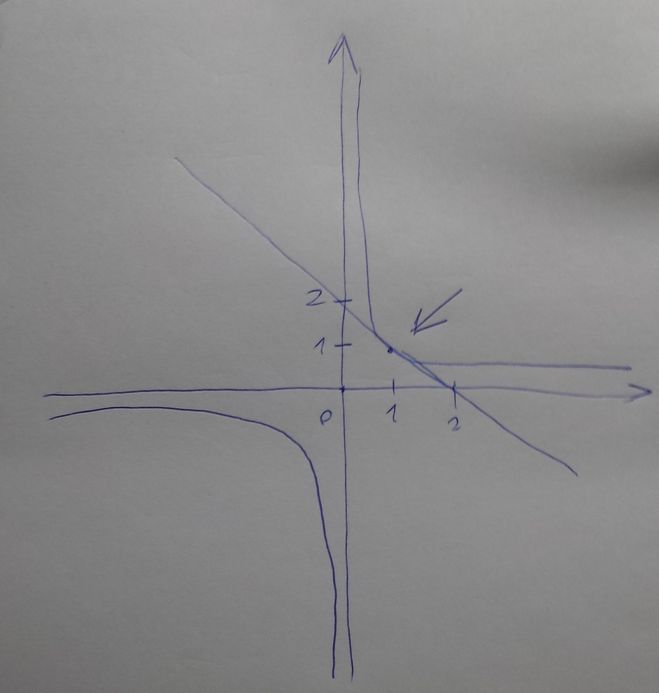
Теперь уже неравенство нам не нужно и мы переходим к системе уравнений, что бы вычислить данную точку — y=2-x;y=1/x — данную систему уравнений уже просто решить — 2-x=1/x отсюда следует, что x(2-x)=1 следовательно -x^2+2x-1=0 стандартное квадратное уравнение (мог расписать его решение, но мне лень), корень которого x=1, корень тут всего 1 оказался.
Значение x мы знаем теперь подставляем его в x+y=2, следовательно 1+y=2 отсюда следует, что y=1. Теперь зная x и y можно без труда вычислить z — xy-z^2=1 следовательно z^2=0 а следовательно z=0. Вот вам и решение x=1 y=1 z=0.
![]()
Значение выражений со степенями находятся разными способами. Самый рациональный из них использование свойств степеней. Пример, решение приведенное автором предыдущего ответа.
Можно найти значение данного выражения 3¹⁷*6¹⁶/18¹⁵ чуть по другому. 3¹⁷*6¹⁶/18¹⁵ = 3¹*3¹⁶*6¹⁶/18¹⁵ = 3¹*(3*6)¹⁶/18¹⁵ = 3¹*18¹⁶/18¹⁵ = 3¹*18¹⁶-¹⁵ =3¹*18¹ = 54.
Но я еще учу детей решать такие примеры «прямым или лобовым» способом (для тех кто не запоминает или не умеет пользоваться свойствами степеней). Им просто надо знать определение степени. Так, 3¹⁷ это 3 умноженное само на себя 17 раз, 6¹⁶ — 6 умноженное на 6 16 раз, 18¹⁵ — соответственно 18 15 раз. Они или выписывают это или представляют себе и начинают сокращать 3 и 6 с 18 и так 15 раз. После сокращений остается две «3» и одна «6», перемножают их и получают ответ 54.
![]()
Но это же очень простая задача! Если 1 гран равен 0,057 современного грамма, то 10 в степени 7 будет во столько же раз больше. То есть 0,057 г следует умножить на 10^7, то есть на 10 миллионов. Проще всего использовать именно показатели степени: 5,7*10^-2 x 10^7 = 5,7*10^5 г. Переводим граммы в килограммы, то есть убираем три нуля и получаем 5,7*10^2 = 570 кг. Немногим больше, чем полтонны. Но вообще задача странная, очень далекая от практики: кто же в Древней Греции выражал бы такой большой вес в гранах! Для этого были другие, более подходящие единицы. Например, талант, который был равен 36 кг.
![]()
А что тут понимать.
В первом случае сложение, 8 плюс 6, 8 плюс 7, 8 плюс 8, 8 плюс 3. Получаются числа 14, 15, 16, 11.
Далее вычитание. 30-16, 50-16, 90-16. Получаются числа 14, 34, 74.
Второй класс, изучают меньше и больше, сложение и вычитание.
![]()
Чтобы найти корень уравнения, надо понять следующий процесс — кубический корень извлекаем из какого-то числа, а это (извлечённое) число возводим в третью степень (то есть в куб) и получаем число под кубическим корнем.
Например куб.корень из 64 равен
³√64 = 4,
а наоборот 4 в кубе будет
4³ = 64; 4х4х4 = 64.
Теперь решаем наше уравнение (x-6)^(1/3) = 2
Нам надо возвести в куб обе стороны уравнения и тогда его будет проще решать.
³√ x-6 = 2
У нас получится такое равенство:
слева останется Х — 6, а справа 2³
Значит: X — 6 = 8
Дальше переносим шестёрку и получаем:
X = 8 + 6;
Х = 14.
Проверяем уравнение: (14 — 6)^(1/3) = 2;
8^(1/3) = 2;
³√8 = 2.
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.
Решение задачи

В данном уроке демонстрируется решение задачи с применением формулы площади прямоугольника, которое можно использовать при подготовке к ОГЭ в качестве примера при решении задач типа ОГЭ 17.
Так, площадь прямоугольника определяется как произведение его сторон. Для определения ширины дорожки вычисляется площадь прямоугольника (дом вместе с дорожкой). Одна сторона прямоугольника выражается как сумма стороны дома и ширины дорожки, уложенной вокруг дома, и равняется . Другая сторона соответственно . Таким образом, площадь прямоугольника вычисляется по выведенной формуле: . Так как площадь прямоугольника задана условием задачи, ширина дорожки
определяется путем решения полученного квадратного уравнения.
Разбирая задания, делаем по шагам. Как можно подробнее, чтобы решали даже самые неуверенные ученики.
1 Задание.
Оно всегда несложное. Тут текст хорошо понятен и обычно ученики без проблем расставляют цифры правильно:
2 Задание.
Предлагаю способ:
1. Найти цветник на плане (номер – 4)
2. Посчитать из скольких клеток он состоит (Площадь – это внутри. Занимает – 8 клеток)
3. Площадь клетки 4 кв.м (2м*2м=4 кв.м)
Далее перемножаем:
3 Задание.
Это задание затруднительно визуально. Чтобы посчитать все плитки которыми выкладываются дорожки, можно определить “единичку” счета.
Клетку на плане (2м*2м) мы разделим на четыре ровные части. Получим клетку (1м*1м). В ней имеем 4 плитки, так как они 50 на 50 см.
Посчитав ими дорожки, получим 51. И далее умножим на 4. Получается 204 плитки, которые делим на 8 (в упаковке).
Когда записываем ответ проверяем в правильную ли сторону округлили. Лучше плитка останется, чем не хватит.
4 Задание.
Найдём расстояние, как гипотенузу в прямоугольном треугольнике, по теореме Пифагора. Если считаем сначала клетками, то не забываем умножить на 2 м, перед тем как давать ответ.
5 Задание.
Сначала это задание кажется сложным, но после тренировок его решают большинство учеников.
1. Умножением крайних столбцов, находим цену газа за час (5,28р) и цену “электрики” за час (25,52р).
2. Находим разницу между ним. То есть каждый час “электрика” больше на 20,24р.
3. Установка газового оборудования (28000 + 16540 = 44540р); установка электрического оборудования (22000 + 14444 = 36444р)
4. Газовое оборудование дороже на 8096р (44540 – 36444)
5. Делением получаем 400 часов, через которые компенсируется данная разница (8096 : 20,24)
Подписывайтесь на канал, ставьте класс, добавляйтесь в группу в контакте, там много полезного.
Если нашли ошибку, дайте мне знать.
Ответ: 1) 4; 2) 54; 3) 2,25.
1.
Поскольку клумбы имеют ромбовидную форму, на схеме они обозначены цифрой 6.
- Площадь (S) ромба вычисляется по формуле: S =
d₁·d₂, где d₁ и d₂ – диагонали ромба.
d₁ = 4кл. = 4м
d₂ = 2кл. = 2м
S = ·4м·2м = 4м²
2.
Найдём площадь площадки, как сумму двух прямоугольников, которые её составляют.
- Площадь (S) прямоугольника вычисляется по формуле: S = a·b, где a и b – смежные стороны прямоугольника.
4·8 + 2·8 = 32+16 = 48 м².
Плодащь одной плитки: 0,1·0,2 = 0,02 м².
Всего понадобится 48:0,02 = 2400 шт. плиток.
В одной пачке 45 штук, тогда понадобится 2400:45 = 53,(3) пачек. Плиток должно хватить, а число пачек может быть только натуральным, поэтому нужно 54 пачки.
3.
Из условия следует, что на плане цифрой 3 отмечен бассейн. Бассейн и беседки имеют форму круга. Любой круг подобен другому кругу. Площади подобных фигур относятся, как коэффициент подобия.
Радиус бассейн 3 клетки, а радиус беседки 2 клетки. Поэтому форма бассейна подобна форме беседки с k=3:2=1,5.
Тогда площадь бассейна в 1,5²=2,25 раза больше площади беседки.
Приложения: