Колбы большинства ЛН – это стеклянные баллоны разной формы, в которые впаивают смонтированные ножки. На рис.6 приведены части и обозначения основных размеров колбы: 1 – основная часть колбы; 2 – горло колбы; 3 – рант.

Назначение колбы – надежно защищать тело накала от атмосферного воздуха; в максимальной степени пропускать оптическое излучение в течении всего срока службы; выполнять роль конструктивного остова лампы, связывая с собой заданным образом ножку и цоколь; в ряде случаев обеспечивать функции оптической системы; выполнять некоторые эстетические функции.
Определение температуры колбы ТК следует проводить в согласии с принятыми принципами расчета ТК колб разрядных ламп.
Так как
КРЛ = qАК,
где К – доля мощности лампы (РЛ), идущая на нагрев колбы; q – удельные тепловые потери колбы путем лучеиспускания (qИ) и отвода тепла через газ (qТ), а АК – площадь внешней колбы (АК = zdК, где dК – диаметр колбы; z – коэффициент, учитывающий реальную форму колбы и зону горловины), то

где Фе – поток излучения ТН; РГ – мощность тепловых потерь ТН через газ; РЦ – мощность, идущая на нагрев цоколя излучением и газом; К – эффективный коэффициент поглощения и излучения стеклом колбы; К – коэффициент, показывающий, какая часть РГ, падающая на колбу, поглощается стеклом; К, К – доли Фе и РГ, падающие на колбу лампы; К – доля РЦ, передаваемая цоколем колбе лампы; А – коэффициент, зависящий, в основном, от рода и давления окружающего колбу газа; ТК – средняя температура колбы, К; ТО – температура окружающей среды, К; К – коэффициент излучения стекла колбы; 0 – постоянная Стефана-Больцмана, равная 5,6710-12 Вт/см2град.
Колбы ламп накаливания выполняются либо из стекла какой-либо группы, либо из кварца. В зависимости от того, с каким металлом стекло образует согласованный спай, стекла разделяют на следующие основные группы:
1) вольфрамовую (СЛ40), 2) молибденовую (СЛ 52), 3) платинитовую (СЛ 96), переходную (СЛ 58, СЛ 86). Кварцевое стекло (СЛ 5) применяется при изготовлении галогенных ламп накаливания, температура стенки которых должна быть около 500 – 600 C.
Итак, в качестве материала колбы выберем стекло, форма колбы – цилиндрическая.
Температура окружающей среды ТО = 25 оС;
Эффективный коэффициент поглощения излучения стеклом колбы К = 0,1.
От положения лампы в пространстве зависит ход конвекционных потоков в лампе и, соответственно, распределение температуры по поверхности колбы. Поэтому в расчете средней температуры колбы задается положение горения лампы: цоколем вверх или цоколем вниз.
Положение горения лампы – цоколем вниз.
Зададимся для расчета некоторыми коэффициентами.
Доля РГ, передаваемая колбе лампы К = 0,7;
Доля Фе падающего на колбу лампы К = 0,9;
Доля РЦ передаваемой цоколем колбе К = 0,08;
Поток излучения телом накала Фе = 79,9 Вт;
Мощность тепловых потерь ТН через газ (РГ) = 0 Вт.
В общем случае мощность идущая на нагрев цоколя излучением и газом:

РЦ = 8 Вт.
В табл.4 приведена зависимость коэффициента А для воздуха от температуры.
Таблица 4.
|
t, оС |
-50 |
0 |
20 |
40 |
60 |
100 |
200 |
|
А*10-4 |
4.6 |
4.4 |
4.2 |
4.2 |
4.1 |
4.0 |
3.7 |
Таким образом, А = 4.210-4.
Если учесть, что площадь горловины колбы АГ обычно связана определенным отношением с площадью шаровой (или считающейся шаровой) частью колбы АК (АК = АГ + АК), то реальный диаметр колбы


где АЦ – площадь поперечного сечения горловины колбы.
Выше приведенные уравнения при принятых ТК позволяют найти dК. Учитывая, что q = f (dК, ТК) данные уравнения решаются графически.
В таблице 5 приведены результаты расчета программы.
Таблица 5.
|
X |
Y1 |
Y2 |
|
50 |
5,600 |
7,264 |
|
75 |
5,600 |
5,336 |
|
100 |
5,600 |
4,229 |
|
125 |
5,600 |
3,629 |
|
150 |
5,600 |
3,155 |
|
175 |
5,600 |
2,794 |
|
200 |
5,600 |
2,51 |
|
225 |
5,600 |
2,278 |
|
250 |
5,600 |
2,084 |
|
275 |
5,600 |
1,919 |
|
300 |
5,600 |
1,775 |
|
325 |
5,600 |
1,651 |
|
350 |
5,600 |
1,541 |
По данным таблицы построим график.

Рис. 7.
По пересечению кривых находим среднюю температуру колбы ТК = 70,3 0С.
2019-12-20 ![]()
Полость теплоизолирующих стенок колбы термоса откачана до давления $p = 10^{-5} атм$ (при комнатной температуре). Вместимость колбы 1 литр, площадь поверхности колбы $S = 600 см^{2}$. Оценить время, в течение которого чай в таком термосе остынет с $90^{ circ} С$ до $70^{ circ} С$. Теплоемкость воды $c = 4,2 cdot 10^{3} Дж/(кг cdot К)$; универсальная газовая постоянная $R = 8,3 Дж/(К cdot моль)$. Утечку тепла через пробку не учитывать.
Решение:
Отвод тепла от внутренней стенки колбы (от чая) осуществляется молекулами газа, оставшегося в полости между внутренней и внешней стенками колбы. Для того и откачивают полость стенок, чтобы оставшийся там газ не образовывал сплошной теплопроводной среды, то есть чтобы молекулы двигались между стенками без столкновения друг с другом.
Будем считать, что после столкновения со стенкой молекула имеет в среднем энергию, пропорциональную температуре стенки. После удара о внешнюю стенку кинетическая энергия поступательного движения молекулы $epsilon_{1} sim frac{3}{2} kT_{к}$, где $T_{к}$ – комнатная температура, после удара о внутреннюю стенку $epsilon_{2} sim frac{3}{2} kT^{ prime}$, где $T^{ prime}$ – температура чая. Эта температура все время меняется. Однако интервал изменения $T^{ prime}$ невелик ($Delta T = 363 К – 343 К = 20 К$). Поэтому для оценки можно считать, что $epsilon_{1} sim 3/2 kT_{с}$, где $T_{с} = 353 К$ – среднее значение температуры горячей стенки.
Следовательно, каждая молекула при ударе о горячую стенку “забирает” от чая энергию
$Delta epsilon sim frac{3}{2} k(T_{с} – T_{к} )$.
Число молекул, соударяющихся с горячей стенкой за единицу времени, пропорционально $frac{1}{2} n | bar{v}_{x} | S$, где $n$ – плотность молекул газа, $| bar{v}_{x} |$ – среднее значение модуля проекции скорости молекулы на ось $OX$, перпендикулярную стенке. Число молекул, ударившихся о стенку за время $Delta t$.
$N sim frac{1}{2} n | bar{v}_{x} | S Delta t$.
Эти молекулы заберут от чая энергию
$Delta E = N Delta e sim frac{3}{4} n | bar{v}_{x} | Sk (T_{с} – T_{к} ) Delta t$.
Очевидно, что эта энергия равна изменению $Delta U$ внутренней энергии чая за время $Delta t: Delta E = Delta U$. Так как
$Delta U = Mc Delta T$,
где $Delta T$ – изменение температуры чая,
$frac{3}{4} n | bar{v}_{x} | Sk (T_{с} – T_{к} ) Delta t sin Mc Delta T$,
Отсюда
$Delta t sim frac{4Mc Delta T}{3n | bar{v}_{x} | Sk (T_{с} – T_{к} ) }$.
Считая что, $| bar{v}_{x} | sim sqrt{ frac{RT_{к} }{ mu}}$, и учитывая, что $n = frac{p}{kT_{к} }$ (это следует из уравнения Менделеева- Клапейрона), окончательно находим
$Delta t sim frac{4Mc Delta T sqrt{ mu T_{к} } }{3p(T_{с} – T_{к} )S sqrt{R} }$.
Подставляя числовые значения ($M = 1 кг, Delta T = 20 К, T_{к} = 293 К, p = 1 Па, mu = 29 cdot 10^{-3} кг/моль$ и т. д.), получим
$Delta t sim 3 cdot 10^{4} с sim 10 ч$.
Как рассчитать объем цилиндра
На данной странице калькулятор поможет рассчитать объем цилиндра онлайн. Для расчета задайте высоту, радиус или площадь основания. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.
Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
По высоте и радиусу
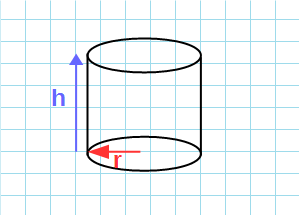
Формула объема цилиндра через высоту и радиус:
V=π·r²·h
π – константа равная (3.14); r – радиус основания; h – высота цилиндра.
Через площадь основания и высоту
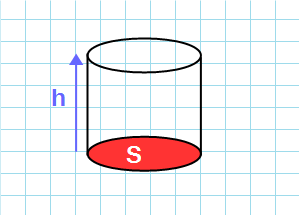
Формула объема цилиндра через высоту и площадь основания:
V=S·h
S – площадь основания цилиндра; h – высота цилиндра.
Содержание
- 1 Как высчитать площадь бочки?
- 2 Как можно узнать объем емкости?
- 3 Как посчитать площадь цилиндра формула?
- 4 Как узнать объем бочки формула?
- 5 Как найти площадь колодца?
- 6 Как вычислить площадь полной поверхности цилиндра?
- 7 Как вычислить объем круглой емкости?
- 8 Как определить емкость рынка?
- 9 Как узнать сколько литров?
- 10 Как рассчитать площадь прутка?
- 11 Как найти площадь цилиндра зная радиус и высоту?
- 12 Как найти радиус цилиндра через площадь?
- 13 Какой объем бочки?
- 14 Как рассчитать объем цилиндрической бочки?
Как высчитать площадь бочки?
Площадь боковой поверхности цилиндра равна произведению высоты цилиндра на длину окружности основания. где R — радиус окружности основания, h — высота цилиндра. Полная площадь поверхности цилиндра равна сумме боковой поверхности цилиндра и двойной площади основания цилиндра.
Как можно узнать объем емкости?
Замеряем глубину резервуара, высоту и ширину в сантиметрах. К примеру, у нас получились следующие параметры: глубина – 50 см, высота – 60 см и ширина – 100 см. Согласно этим размерами, объем аквариума рассчитывается по формуле (V=X*Y*H) или 100х50х60=3000000 см³.
Как посчитать площадь цилиндра формула?
Сторонами этого прямоугольника будут длина окружности(L = 2πr) и высота цилиндра(h). Площадь прямоугольника равна произведению его сторон – S = длина х ширина = L x h = 2πr x h = 2πrh. В результате мы получили формулу для расчета площади боковой поверхности цилиндра.
Как узнать объем бочки формула?
1) Объем цилиндра равен произведению площади основания на высоту. 2) Объем цилиндра равен произведению числа пи (3.1415) на квадрат радиуса основания на высоту.
Как найти площадь колодца?
V = π * d * l / 1000
На этой странице представлен простой онлайн калькулятор расчета площади колодца в м2 (квадратных метрах) по простой математической формуле в зависимости от диаметра и высоты колодца. С помощью этой программы вы в один клик сможете рассчитать площадь колодца в м2.
Как вычислить площадь полной поверхности цилиндра?
Площадь полной поверхности цилиндра через радиус основания и высоту Формула для нахождения полной поверхности цилиндра через высоту и радиус основания: S = 2 π r ( h + r ) {S = 2pi r (h+r)} S=2πr(h+r), где π — число Пи (3,14159…), r — радиус основания цилиндра, h — высота цилиндра.
Как вычислить объем круглой емкости?
Возьмите рулетку или верёвку и расположите её возле стенки на дне, а другой конец протяните к противоположной стороне. Диаметр ёмкости в два раза больше, чем её радиус. Поэтому данные нужно будет разделить на 2.
…
π – равно 3,14;
- R – это радиус дна ёмкости;
- H – её высота;
- V – это объем сосуда, который имеет круглую форму.
Как определить емкость рынка?
Математически, ёмкость рынка можно выразить следующим образом: Е = М х С; где: Е — емкость рынка в натуральном или денежном выражении (ед./год, руб./год.); М — количество реализуемого товара в год (ед.);
Как узнать сколько литров?
Объем измеряется в кубических единицах, например, в кубических сантиметрах (см3). Преобразуйте кубические сантиметры в литры. Для этого воспользуйтесь следующим соотношением: 1 л = 1000 см3. Разделите объем, измеренный в кубических сантиметрах, на 1000, чтобы получить объем в литрах (л).
Как рассчитать площадь прутка?
S = π * d 2 / 4, где
На этой странице представлен самый простой онлайн калькулятор расчета площади поперечного сечения прутка, если известен диаметр прутка. С помощью этого калькулятора вы в один клик сможете рассчитать площадь сечения прутка.
Как найти площадь цилиндра зная радиус и высоту?
Площадь боковой поверхности цилиндра, зная высоту и площадь основания, можно найти, выразив радиус через площадь основания и умножив его на удвоенное число π и высоту, а площадь полной поверхности будет представлена как сумма этого значения и двух заданных площадей основания.
Как найти радиус цилиндра через площадь?
Калькулятор вычисляет радиус цилиндра по сложной формуле, используя исходные данные площади цилиндра и его высоты: r=(sqrt(8 х pi х S+sqrt(2 х pi х h)) — 2 х pi х h)/2 х pi.
Какой объем бочки?
Большая часть бочек имеет стандартный объём 208 литров, что соответствует 55 галлонам (США)или 44 имперским галлонам (Великобритания). Бочка имеет следующие габаритные размеры: высота — 800 мм, диаметр — до 550 мм.
Как рассчитать объем цилиндрической бочки?
Формула расчета объема цилиндрической емкости (цилиндра)
- V=S*L — расчет объема цилиндра, …
- S=3,14*d*d/4 — площадь круга с диаметром d.
- Расчет объема цилиндрической емкости по формуле можно сделать как для горизонтальной, так и вертикальной накопительной емкости по их расположению. …
- d=Lокр/3,14.
Содержание
- ГДЗ учебник по физике 7 класс Перышкин. №4 Измерение объема тела. Номер №1
- Решение
- ГДЗ учебник по физике 7 класс Перышкин. №1 Определение цены деления измеррительного прибора. Номер №1
- Решение
- Расчет объёма жидкости в прямоугольной емкости
- Инструкция для онлайн калькулятора расчета объема жидкости в прямоугольной емкости (типа аквариума)
- Как рассчитать объём — калькулятор объёма куба, прямоугольной ёмкости, объёма цилиндра, объёма воды в трубе …
- Как рассчитать объём любой прямоугольной емкости, в том числе куба — онлайн калькулятор расчёта объема воды в аквариуме, баке …
- Формула расчёта объёма прямоугольной ёмкости
- Как рассчитать объём цилиндра — онлайн калькулятор расчёта объёма воды в трубе, бочке, круглом бассейне …
- Формулы расчёта объёма цилиндра:
- Единицы измерения объёма
- Соотношение единиц объёма
- Конвертер единиц объёма
- Конвертация кубических метров ( м 3 ) в кубические сантиметры ( см 3 ) и литры
- Конвертация литров в метры кубические ( м 3 ) и кубические сантиметры ( см 3 )
- Конвертация кубических сантиметров ( см 3 ) в кубические метры ( м 3 ) и литры
- Заключение
- Как рассчитать объём — калькулятор объёма куба, прямоугольной ёмкости, объёма цилиндра, объёма воды в трубе …
- 1 комментарий к “Как рассчитать объём — калькулятор объёма куба, прямоугольной ёмкости, объёма цилиндра, объёма воды в трубе …”
- Оставьте комментарий Отменить ответ
- Поделись с друзьями 🙂
- Рубрики сайта
- Публикации
- Публикации
- Свежие комментарии
- Поиск по сайту
ГДЗ учебник по физике 7 класс Перышкин. №4 Измерение объема тела. Номер №1
Цель работы:
Научиться определять объём тела с помощью измерительного цилиндра.
Приборы и материалы:
Измерительный цилиндр (мензурка), тела неправильной формы небольшого объёма (гайки, фарфоровые ролики, кусочки металла и др.), нитки.
Указания к работе:
1 . Определите цену деления мензурки.
2 . Налейте в мензурки столько воды, чтобы тело можно было полностью погрузить в воду, и измерьте её объём.
3 . Опустите тело, объём которого надо измерить, в воду, удерживая его за нитку (рис. 201 ), и снова измерьте объём жидкости.
4 . Проделайте опыты, описанные в пунктах 2 и 3, с некоторыми другими имеющимися у вас телами.
5 . Результаты измерений запишите в таблицу 9 .
Дополнительное задание.
Если тело неправильной формы не входить в мензурку, то его объём можно определить с помощью отливного сосуда (рис. 202 ). Перед измерением сосуд наполняют водой до отверстия отливной трубки. При погружении в него тела часть воды, равная объёму тела, выливается. Измерив мензуркой её объём, определяют объём погружённого в жидкость тела.
Таблица 9 . 
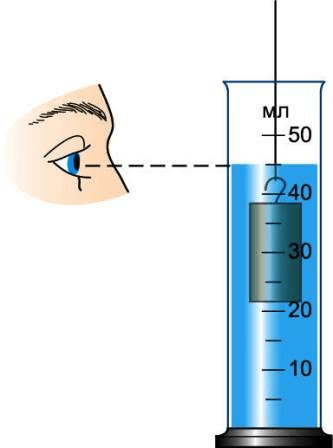
рис. 201
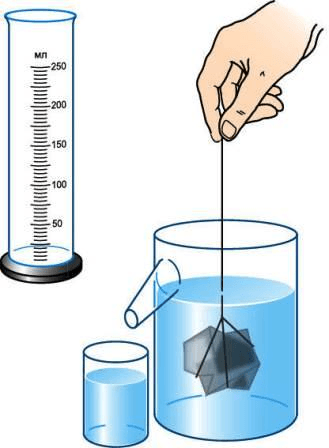
рис. 202
Решение
Объём тела неправильной формы точно измерить с помощью измерительных приборов нельзя. Поэтому для измерения объема воспользуемся мензуркой. Тело, полностью погружённое в жидкость, вытесняет объём жидкости, который равен объёму самого тела. Воспользуемся этим законом и найдем объёмы некоторых тел следующим образом. Нальем достаточное количество воды в мензурку, а затем погрузим полностью туда наше тело. Разница между первоначальным объёмом и объёмом жидкости, в которое погружено тело, равна объёму этого тела.
$V = V_ <2>— V_<1>$ , где $V_<2>$ − объём воды и тела, $V_<1>$ − начальный объём воды в мензурке.
- Прежде чем проводить измерения физической величины с помощью измерительного прибора нужно определите цену деления его шкалы.
Для определения цены деления необходимо взять 2 соседних числа, найти их разницу (от большего отнять меньшее), а затем разделить полученное число на количество маленьких штрихов между этими числами.
На шкале цилиндра возьмём, к примеру, числа 20 и 30 .
Таким образом, цена каждого деления будет равна
$frac<30 – 20><2>= frac<10><2>$ = 5 мл. - В мензурку нальём столько воды, чтобы тело можно было полностью погрузить в воду. Начальный объём воды равен 70 $см^<3>$ .
- Опустим тело, объём которого надо измерить (шарик, брусок, цилиндр), в воду, удерживая его за нитку, и снова измерим объём жидкости.
Вычисления.
$V_ <бр>= 95 — 70 = 25 см^<3>$
$V_ <ц>= 85 — 65 = 20 см^<3>$
$V_ <ш>= 75 — 60 = 15 см^<3>$ - Результаты измерений запишем в таблицу 9 .
| № опыта | Название тела | Начальный объём воды в мензурке $V_<1>, см^<3>$ | Объём воды и тела $V_<2>, см^<3>$ | Объём тела V, $см^<3>$ $V = V_<2>-V <1>$ |
|---|---|---|---|---|
| 1 | Брусок | 70 | 95 | 25 |
| 2 | Цилиндр | 65 | 85 | 20 |
| 3 | Шарик | 60 | 75 | 15 |
Вывод. В ходе лабораторной работы мы научились измерять объёмы тел с помощью измерительного цилиндра и выяснили, что объём тел равен разнице объёма воды, в которое погружено тело, и первоначального объёма воды.
Источник
ГДЗ учебник по физике 7 класс Перышкин. №1 Определение цены деления измеррительного прибора. Номер №1
Цель работы:
Определить цену деления измерительного цилиндра (мензурки), научиться пользоваться им и определять с его помощью объём жидкости.
Приборы и материалы:
Измерительный цилиндр (мензурка), стакан с водой, небольшая колба и другие сосуды.
Указания к работе:
1 . Рассмотрите измерительный цилиндр (рис. 198 ), обратите внимание на его деления. Ответьте на следующие вопросы.
1 )Какой объём жидкости вмещает измерительный цилиндр, если жидкость налита:
а) до верхнего штриха;
б) до первого снизу штриха, обозначенного цифрой, отличной от нуля?
2 )Какой объём жидкости помещается:
а) между 2 −м и 3 −м штрихами, обозначенными цифрами;
б) между соседними (самыми близкими) штрихами мензурки?
2 . Как называется последняя вычисленная вами величина? Как определяют цену деления шкалы измерительного прибора?
Запомните: прежде чем проводить измерения физической величины с помощью измерительного прибора, определите цену деления его шкалы.
3 . Рассмотрите рисунок 7 учебника и определите цену деления изображённой на нём мензурки.
4 . Налейте в измерительный цилиндр воды, определите и запишите, чему равен объём налитой воды.
Примечание. Обратите внимание на правильное положение глаза при отсчёте объёма жидкости. Вода у стенок сосуда немного приподнимается, в средней же части сосуда поверхность жидкости почти плоская. Глаз следует направить на деление, совпадающее с плоской частью поверхности (рис. 198 ).
5 . Налейте полный стакан воды, потом осторожно перелейте воду в измерительный цилиндр. Определите и запишите с учётом погрешности, чему равен объём налитой воды. Вместимость стакана будет такой же.
6 . Таким же образом определите вместимость колбы, аптечных склянок и других сосудов, которые находятся на вашем столе.
7 . Результаты измерений запишите в таблицу 6 . 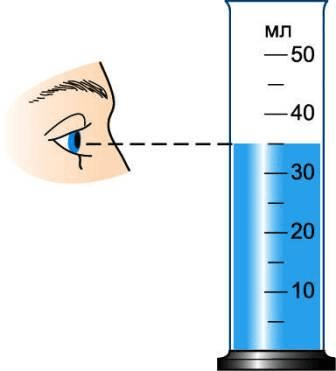
рис. 198 . 
рис. 7 . Измерительный цилиндр.
Таблица 6 . 
Решение
Прежде чем проводить измерения физической величины с помощью измерительного прибора нужно определите цену деления его шкалы.
Для определения цены деления необходимо взять 2 соседних числа, найти их разницу (от большего отнять меньшее), а затем разделить полученное число на количество маленьких штрихов между этими числами.
На шкале цилиндра возьмём, к примеру, числа 20 и 30 .
Таким образом, цена каждого деления будет равна
$frac<30 – 20> <2>= frac<10><2>$ = 5 мл.
1 .
1, а) Если жидкость налита до верхнего штриха, измерительный цилиндр вмещает 50 мл жидкости.
1, б) Если жидкость налита до первого снизу штриха, обозначенного цифрой, отличной от нуля, измерительный цилиндр вмещает 10 мл жидкости.
2, а) Между 2 − м и 3 −м штрихами, обозначенными цифрами, помещается 10 мл жидкости (например, возьмём штрихи 20 мл и 30 мл).
2, б) Между соседними (самыми близкими) штрихами мензурки (например, возьмём штрихи 30 и 35 ), помещается 5 мл жидкости.
2 . Последняя вычисленная нами величина является ценой деления измерительного цилиндра.
3 . На шкале цилиндра возьмём, к примеру, числа 50 и 60 . Количество маленьких штрихов между этими числами − 2 .
Таким образом, цена каждого деления будет равна
$frac<60 – 50> <2>= frac<10><2>$ = 5 мл.
4 . Объём налитой воды равен 35 мл или 35 $см^<3>$ .
5 . Погрешность измерений равна половине цены деления шкалы измерительного прибора. Цена деления цилиндра − 5 мл, следовательно, погрешность измерения равна $frac<5><2>$ мл = 2,5 мл.
Объём налитой в полный стакан воды с учётом погрешности будет равен ( 200 ±∆ 2,5 ) мл ( $см^<3>$ ).
6 .
Таблица 6 .
| № опыта |Название сосуда| Объём жидкости $V_<ж>, см^<3>$ |Вместимость сосуда, $V_<с>, см^<3>$ |
| −−− | −−− | −−− | −−− |
| 1 | стакан | 200 | 200 |
| 2 | колба | 50 | 50 |
| 3 | пузырёк | 30 | 30 |
Вывод. В ходе лабораторной работы мы определелили цену деления измерительного цилиндра, научились им пользоваться и научились с его помощью определять объём жидкости.
Источник
Расчет объёма жидкости в прямоугольной емкости
Инструкция для онлайн калькулятора расчета объема жидкости в прямоугольной емкости (типа аквариума)
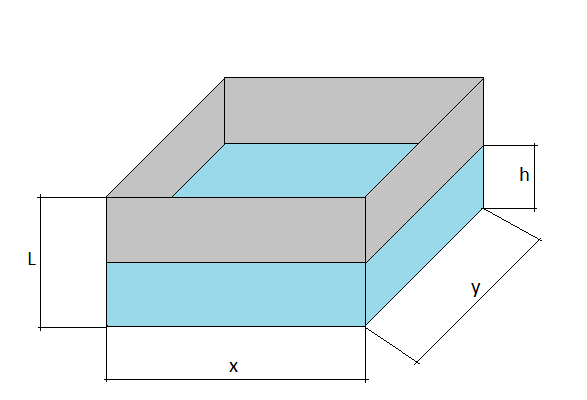
Впишите размеры в миллиметрах:
X – Ширина емкости, поперечное расстояние между стенками.
Y – Длина резервуара, т.е. его протяженность, наибольший линейный размер в продольном направлении.
L – Высота емкости, определяется высотой ее стенок.
h – Высота уровня жидкости, ее определяют мерной линейкой (т.н. метршток), если такого инструмента нет, подойдет обычный стержень из проволоки или дерева подходящей длины. Соблюдая меры безопасности, опустите строго вертикально стержень в цистерну до дна, отметьте на нем уровень, достаньте и измерьте рулеткой. Также определить h можно, измерив, расстояние от верхней точки резервуара до поверхности жидкости и отняв этот показатель от высоты емкости L.
Нажмите «Рассчитать».
Онлайн калькулятор поможет посчитать полный объём емкости и узнать максимальную вместительность резервуара (в м 3 и литрах). Выяснить сколько вещества уже находится в емкости. Значение свободного объёма даст представление, сколько жидкости еще можно залить в емкость. Также программа вычислит площадь дна, площадь боковой поверхности и общую площадь емкости, что поможет легко подсчитать нужное количество материалов для отделки всего резервуара или его частей.
Источник
Как рассчитать объём — калькулятор объёма куба, прямоугольной ёмкости, объёма цилиндра, объёма воды в трубе …

Как рассчитать объём ёмкости, воды или другой жидкости … несколько онлайн калькуляторов для расчёта объёма, формулы, а также конвертер единиц объёма.
Как рассчитать объём любой прямоугольной емкости, в том числе куба — онлайн калькулятор расчёта объема воды в аквариуме, баке …
Формула расчёта объёма прямоугольной ёмкости
V = X * Y * Z, где V — объём, а X, Y, и Z это длины сторон ёмкости (длина, ширина, высота).
При этом мы помним, что у куба все стороны равны — X=Y=Z . Соответственно формула объёма куба имеет такой вид — V = X 3 , где X — длина стороны куба.
Внимание! При расчёте объёма жидкости в ёмкости необходимо учитывать реальную заполненность ёмкости и привязывать величины непосредственно к самой жидкости.
Для конвертации единиц объёма вы можете воспользоваться нашим ОНЛАЙН КОНВЕРТЕРОМ ЕДИНИЦ ОБЪЁМА →
Как рассчитать объём цилиндра — онлайн калькулятор расчёта объёма воды в трубе, бочке, круглом бассейне …
Для конвертации единиц объёма вы можете воспользоваться нашим ОНЛАЙН КОНВЕРТЕРОМ ЕДИНИЦ ОБЪЁМА →
Формулы расчёта объёма цилиндра:
Объём воды в цилиндре и других ёмкостях, имеющих цилиндрическую форму, рассчитывается таким образом.
Вначале рассчитываем площадь основания (площадь внутреннего сечения) по формуле — S = π * R 2
Где, R — радиус трубы, π — число ПИ равное 3,1415926535 .
Затем вычисляем объём — V = S * L
Где, L — длина (высота) цилиндра (трубы, бочки, бассейна).
Внимание! При расчёте объёма жидкости в ёмкости необходимо учитывать заполненность ёмкости и привязывать величины непосредственно к самой жидкости.
Единицы измерения объёма
Вначале кратко ознакомимся с единицами измерения объёма как таковыми.
Официальной единицей измерения объема в системе СИ является м 3 — метр кубической. Объём так же может быть выражен и в других единицах. Наиболее популярными из них являются — дм 3 — кубические дециметры, см 3 — кубические сантиметры, литры …
Отметим, что такая популярная единица измерения объёма жидкостей как литр не входит в Международную систему измерений (СИ). Тем не менее, поскольку литр является весьма популярной мерой жидкостей, он считается официальной внесистемной единицей.
Один литр — это объём куба стороны которого равны 10 см. Полезно также знать, что 1 литр воды вести приблизительно 1 кг при температуре + 4 °C
Соотношение единиц объёма
1 м3 = 1000 дм 3 = 1 000 000 см 3 = 1 000 000 000 мм 3 = 1000 литров
1 литр = 0,001 м 3 = 1 дм 3 = 1 000 см 3 = 1 000 000 мм 3
Конвертер единиц объёма
Конвертация кубических метров ( м 3 ) в кубические сантиметры ( см 3 ) и литры
Конвертация литров в метры кубические ( м 3 ) и кубические сантиметры ( см 3 )
Конвертация кубических сантиметров ( см 3 ) в кубические метры ( м 3 ) и литры
Заключение
Практически каждый человек рано или поздно сталкивается с необходимостью рассчитать объём того или другого объекта. Для удобства и экономии времени предлагаем Вам воспользоваться нашими онлайн калькуляторами.
Как рассчитать объём — калькулятор объёма куба, прямоугольной ёмкости, объёма цилиндра, объёма воды в трубе …

1 комментарий к “Как рассчитать объём — калькулятор объёма куба, прямоугольной ёмкости, объёма цилиндра, объёма воды в трубе …”
Быстро и удобно если много объёмов
Оставьте комментарий Отменить ответ
Поделись с друзьями 🙂
Рубрики сайта
Публикации
Публикации
Свежие комментарии
Поиск по сайту
Концепция и реализация проекта О воде | H2O и Водных ресурсах мира © vodamama.com 2014 — 2021
Политика конфиденциальности / Условия и положения использования сайта — Privacy policy / Terms and conditions
Все материалы сайта защищены Законом «Об авторском праве и смежных правах». Сайт – vodamama.com является общедоступным и работает в рамках и в соответствии с действующим законодательством Украины.
Копирование, перепечатка или воспроизведение любых текстовых материалов, размещенных на сайте vodamama.com , строго запрещается.
Администрация ресурса может не разделять мнение автора. При подготовке материалов информация берётся из общедоступных источников и специальной проверки на достоверность не проходит.
Администрация сайта радикально негативно относится к нарушениям авторских или каких либо других имущественных прав. Поэтому, если Вы вдруг обнаружили, что на страницах нашего сайта нарушены, какие либо авторские или имущественные права, просим вас незамедлительно, воспользовавшись формой обратной связи, сообщить нам про это. После получения подтверждения нарушения мы незамедлительно устраним его.
Источник
