Как найти площадь кольца если известна хорда

Площадь кольца

Онлайн калькулятор

Площадь кольца по радиусам или диаметрам

Чему равна площадь кольца ограниченного двумя окружностями, если:

у внешней окружности
у внутренней окружности

Площадь кольца по толщине и любому другому параметру

Чему равна площадь кольца ограниченного двумя окружностями, если:

толщина кольца t =

Теория

Площадь кольца через радиусы

Чему равна площадь кольца S ограниченного двумя окружностями, если известны радиус внешней окружности R и радиус внутренней окружности r ?

Формула

Пример

К примеру, определим площадь кольца, у которого внешний радиус R = 3 см, а внутренний радиус r = 2 см:

S = 3.14 ⋅ (3² – 2²) = 3.14 ⋅ (9 – 4) = 3.14 ⋅ 5 = 15.7 см²

Ответ: S = 15.7 см²

Площадь кольца через диаметры

Чему равна площадь кольца S ограниченного двумя окружностями, если известны диаметр внешней окружности D и диаметр внутренней окружности d ?

Формула

Пример

К примеру, определим площадь шайбы, внешний диаметр которой D = 4 см, а внутренний – d = 2 см:

S = 3.14 / 4 ⋅ (4² – 2²) = 0.785 ⋅ (16 – 4) = 9.42 см²

Ответ: S = 9.42 см²

Площадь кольца через толщину

Чтобы посчитать площадь кольца S зная его толщину t, необходимо знать ещё какой-нибудь из следующих параметров:

• внешний диаметр D
• внутренний диаметр d
• радиус внешней окружности R
• радиус внутренней окружности r

Формулы

Пример

Для примера, найдём чему равна площадь кольца толщиной t = 2 см и внешним диаметром D = 5 см:

S = 3.14/4 ⋅ (5² – (5 – 2 ⋅ 2)²) = 0.785 ⋅ (25 – 1) = 18.84 см²

№ 54. Найдите площадь кругового кольца, заключенного между двумя окружностями с одним и тем же центром и радиусами: 1) 4 см и 6 см; 2) 5,5 ми 6,5 м; 3) а и b, а > b.

Решебник по геометрии за 9 класс (А.В.Погорелов, 2001 год),
задача №54
к главе «§14. Площади фигур».

Выделите её мышкой и нажмите CTRL + ENTER

Большое спасибо всем, кто помогает делать сайт лучше! =)

Нажмите на значок глаза возле рекламного блока, и блоки станут менее заметны. Работает до перезагрузки страницы.

Найдите площадь кругового кольца, заключенного между двумя концентрическими окружностями, длины которых равны а и b, где а < ; b?

Геометрия | 5 – 9 классы

Найдите площадь кругового кольца, заключенного между двумя концентрическими окружностями, длины которых равны а и b, где а < ; b.

Первая окружность с радиусом R₁

Длина окружности L = 2πR

b = 2πR₁⇒ R₁ = b / 2π

а = 2πR₂ ⇒ R₂ = а / 2π

Площадь окружности S = πR²

площадь кольца равна S₁ – S₂ = π(R₁² – R₂²) = π((b / 2π ) ² – (а / 2π)²) = (b² – а²) / 4π.

Найти площадь кругового сектра(кольца) заключенного между двумя окружностями, с одним и тем же центром и радиусом 4 и 6 см?

Найти площадь кругового сектра(кольца) заключенного между двумя окружностями, с одним и тем же центром и радиусом 4 и 6 см.

(подробно и с объяснением).

Площадь кругового кольца, находящегося между двумя окружностями с общим центром, равна 12дм², радиус одной окружности в 2 раза больше, чем радиус другой?

Площадь кругового кольца, находящегося между двумя окружностями с общим центром, равна 12дм², радиус одной окружности в 2 раза больше, чем радиус другой.

Найдите эти радиусы.

Даны две концентрические окружности, длина одной из них 33п см, а другой 27п см?

Даны две концентрические окружности, длина одной из них 33п см, а другой 27п см.

Найдите ширину кольца.

В кольце, образуемом двумя концентрическими окружностями, проведена хорда, касающаяся меньщей окружности?

В кольце, образуемом двумя концентрическими окружностями, проведена хорда, касающаяся меньщей окружности.

Найдите площадь кольца , если известно, что длина хорды равна 8 см.

Около правильного треугольника описана окружность и в него вписана окружность?

Около правильного треугольника описана окружность и в него вписана окружность.

Длина меньшей окружности равна 8пи.

Найдите площадь кольца и площадь треугольника.

Срочно?

№8. Радиусы двух концентрических окружностей относятся как 4 : 5.

Найдите их диаметры, если ширина кольца, образованного этими окружностями, равна 7 см.

№9. Найдите радиусы двух концентрических окружностей, если известно, что их диаметры относятся как 2 : 5 и ширина кольца, образованного этими окружностями, равна 24 см.

Помогите плииииииииииииииз?

От этой оценки зависит четвертная!

1. Фигура, ограниченная двумя концентрическими окружностями, называется кольцом, а разность радиусов данных окружностей – шириной этого кольца.

1) выразите ширину кольца через длины окружностей

2) радиусы окружностей равны 26см и 10см.

Найдите длину наибольшего отрезка, который целиком можно поместить в данное кольцо

Какую часть площади круга составляет площадь сектора, центральный угол которого равен 1)30°, 2)45°, 3)60°, 4)90°, 5)180°, 6)300°.

Площадь кругового кольца, заключенного между двумя окружностями с одним и тем же центром, равна 8 см2?

Площадь кругового кольца, заключенного между двумя окружностями с одним и тем же центром, равна 8 см2.

Найдите площади этих кругов, ограниченными этими окружностями, если радиус одной из них в три раза больше, чем радиус другой.

В правильный треугольник со стороной 4 см вписана окружность и около него описана окружность?

В правильный треугольник со стороной 4 см вписана окружность и около него описана окружность.

Найдите площадь кольца, заключенного между этими окружностями.

Ширина кольца, образованного концентрическими окружностями радиусов 3 см и 5 см, равна ?

Ширина кольца, образованного концентрическими окружностями радиусов 3 см и 5 см, равна :

На этой странице сайта размещен вопрос Найдите площадь кругового кольца, заключенного между двумя концентрическими окружностями, длины которых равны а и b, где а < ; b? из категории Геометрия с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 5 – 9 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.

МК||АС, АВ – секущая. По свойству углов, образованных при пересечении параллельных прямых секущей соответственные ∠ВМК = ∠ВАС = 80° MN – биссектриса, ∠ВМN = ∠KMN = 80° : 2 = 40° ВС – секущая при параллельных МК и АС. ⇒соответственные ∠ВКМ = ∠ВСА = ..

Ты знаешь чему равна длина отрезка ВС , и знаешь длина АС, и тут ты можешь так. BC – AC = BA 8 – 3 = 5.

З вeршини кута провeдeно промінь , пeрпeндикулярний до його бісeктриси , який утворює зі стороною даного кута гострий кут, градусна міра якого в 4 рази більша за даний кут . Знайдіть даний кут.

Площадь треугольника S = (a²·sinα) / 2, где а – боковая сторона, α – угол при вершине. A² = 2S / sinα = 2·48 / 0. 5 = 192, a = 8√3 см – это ответ.

Периметр прямоугольника рассчитывается по формуле : P = 2(a + b) Подставим значения a и b в формулу и получим : P = 2(10 + 8) = 36 см Ответ : 36 см.

Три прямые пересекаются в одной точке и образуют шесть углов. Найдите сумму трёх из этих углов, которые попарно не имеют общих точек.

Известно : биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим сторонам (в нашем случае – катетам), т. Е. дано отношение катетов 15 : 20 = 3 : 4 отношение катетов – – это тангенс острого угла в прямоугольном треугольнике и..

[spoiler title=”источники:”]

http://5terka.com/node/737

http://geometria.my-dict.ru/q/1739191_najdite-plosad-krugovogo-kolca-zaklucennogo-mezdu/

[/spoiler]

В кольце, образуемом двумя концентрическими окружностями, проведена хорда, касающаяся меньщей окружности. Найдите площадь кольца , если известно, что длина хорды равна 8 см.

Чему равна площадь кольца?

Гений

(54624),
закрыт

15 лет назад

Геометрия 7-9 класс. Площадь круга. Площадь кругового сектораadmin2023-03-28T20:47:18+03:00

Скачать файл в формате pdf.

Геометрия 7-9 класс. Площадь круга. Площадь кругового сектора

Площадь круга радиуса R равна  (S = pi {R^2}.)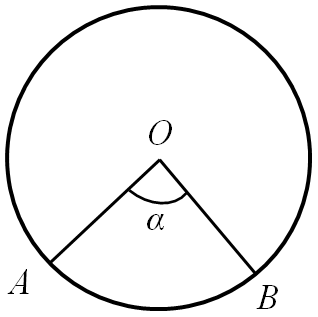

Площадь сектора   ({S_{OAB}} = pi {kern 1pt} {R^2}frac{alpha }{{360}}).

Задача 1. Найдите площадь круга, радиус которого равен (frac{8}{{sqrt {rm{pi }} }}.) Ответ ОТВЕТ: 64.
Задача 2. Найдите радиус круга, если его площадь равна (25{rm{pi }}.) Ответ ОТВЕТ: 5.
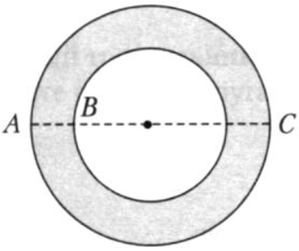
Задача 3. Найдите площадь кольца, если (AB = frac{2}{{sqrt {rm{pi }} }}) и (BC = frac{8}{{sqrt {rm{pi }} }}.) Ответ ОТВЕТ: 16.
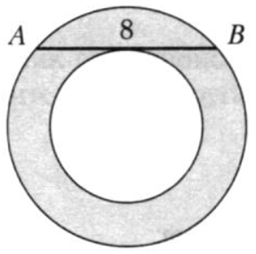
Задача 4. Найдите площадь кольца, если длина хорды (AB = frac{8}{{sqrt {rm{pi }} }}.) Ответ ОТВЕТ: 16.
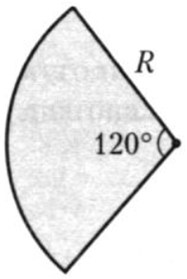
Задача 5. По данным на рисунке найдите R, если площадь сектора равна (12{rm{pi }}.) Ответ ОТВЕТ: 6.
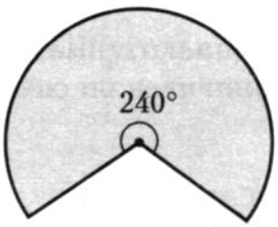
Задача 6. По данным на рисунке найдите площадь сектора, если радиус  равен (frac{6}{{sqrt {rm{pi }} }}.) Ответ ОТВЕТ: 24.
Задача 7. Найдите площадь сектора АОВ с центром в точке О, если длина дуги АВ равна 6 и ОА = 4. Ответ ОТВЕТ: 12.
Задача 8. Найдите радиус окружности ОА с центром в точке О, если длина дуги АВ равна 8, а площадь сектора АОВ равна 40. Ответ ОТВЕТ: 10.
Задача 9. Найдите площадь круга, вписанного в правильный треугольник, стороны которого равны (frac{6}{{sqrt {rm{pi }} }}.) Ответ ОТВЕТ: 3.
Задача 10. Найдите площадь круга, описанного около прямоугольника, стороны которого равны (frac{3}{{sqrt {rm{pi }} }}) и (frac{5}{{sqrt {rm{pi }} }}.) Ответ ОТВЕТ: 8,5.
Задача 11. Сторона АВ является диаметром окружности описанной около треугольника АВС. Найдите площадь круга, если (AC = frac{{12}}{{sqrt {rm{pi }} }},) а (angle B = {60^ circ }.) Ответ ОТВЕТ: 48.
Задача 12. Найдите площадь круга, описанного около квадрата, сторона которого равна (frac{3}{{sqrt {rm{pi }} }}) Ответ ОТВЕТ: 4,5.
Задача 13. Найдите площадь круга, вписанного в равнобедренную трапецию, боковые стороны которого равны 8, а площадь 32. Ответ ОТВЕТ: ({rm{4pi }}.)
Задача 14. В равнобедренной трапеции основания равны 2 и 14, а боковые стороны по 10. Найдите площадь круга, описанного около трапеции. Ответ ОТВЕТ: ({rm{50pi }}.)
Задача 15. Найдите площадь круга, вписанного в ромб, площадь которого равна 40, а один из углов ({30^ circ }.) Ответ ОТВЕТ: ({rm{5pi }}.)
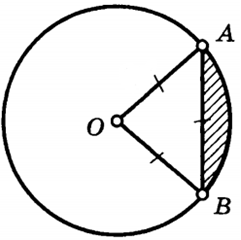
Задача 16. По данным на рисунке найдите площадь заштрихованной фигуры, если ОА = 12 и ОА = АВ. Ответ ОТВЕТ: (12left( {2{rm{pi }} — 3sqrt 3 } right).)
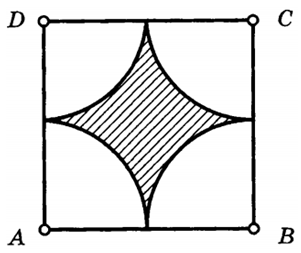
Задача 17. По данным на рисунке найдите площадь заштрихованной фигуры, если ABCD квадрат со стороной 8. Ответ ОТВЕТ: (16left( {4 — {rm{pi }}} right).)
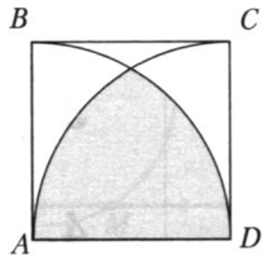
Задача 18. По данным на рисунке найдите площадь закрашенной фигуры, если ABCD квадрат со стороной 8, а АВ и DC радиусы. Ответ ОТВЕТ: (8left( {frac{{8{rm{pi }}}}{3} — 2sqrt 3 } right).)
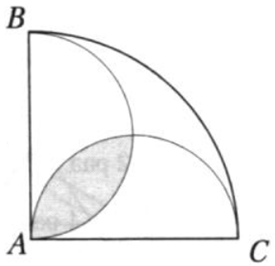
Задача 19. По данным на рисунке найдите площадь закрашенной фигуры, если (angle ,BAC = {90^ circ },) а  АВ и АС радиусы равные 12. Ответ ОТВЕТ: (18left( {{rm{pi }} — 2} right).)