
{S = pi (R^2 – r^2)}
С помощью приведенных калькулятора и формул можно рассчитать площадь кольца через радиусы или диаметры онлайн.
Кольцо — плоская геометрическая фигура, ограниченная двумя концентрическими окружностями.
Содержание:
- калькулятор площади кольца
- формула площади кольца через радиусы
- формула площади кольца через диаметры
- примеры задач
Формула площади кольца через радиусы
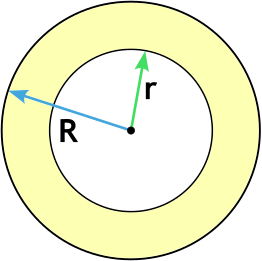
{S = pi (R^2 – r^2)}
R – внешний радиус кольца
r – внутренний радиус кольца
Формула площади кольца через диаметры
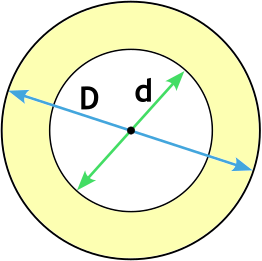
{S= dfrac{pi}{4}(D^2 – d^2)}
D – внешний диаметр кольца
d – внутренний диаметр кольца
Примеры задач на нахождение площади кольца
Задача 1
Найдите площадь кольца ограниченного двумя окружностями с общим центром и радиусами 3 см и 7 см.
Решение
В условии задачи даны радиусы ограничивающих кольцо окружностей, поэтому воспользуемся первой формулой.
S = pi (R^2 – r^2) = pi (7^2 – 3^2) = pi (49 – 9) = 40pi approx 125.66371 : см^2
Ответ: 108 cdot 0.866 approx 93.53074 : см^2
Полученный ответ можно проверить с помощью калькулятора .
Задача 2
Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны dfrac{4}{sqrt{pi}} и dfrac{2}{sqrt{pi}}.
Решение
Задача похожа на предыдущую, поэтому алгоритм ее решения будет тот же.
S = pi (R^2 – r^2) = pi ({Big(dfrac{4}{sqrt{pi}} Big) }^2 – {Big(dfrac{2}{sqrt{pi}} Big) }^2) = pi (dfrac{16}{pi} – dfrac{4}{pi}) = pi dfrac{12}{pi} = 12 : см^2
Ответ: 12 : см^2
Наш калькулятор может производить вычисления с выражениями. Для того, чтобы ввести радиусы из условия их нужно записать в понятном для калькулятора формате:
dfrac{4}{sqrt{pi}} : rarr : 4/sqrt(pi)
dfrac{2}{sqrt{pi}} : rarr : 2/sqrt(pi)
Если ввести данные в таком формате, можно проверить ответ .
Задача 3
Найдите площадь кольца образованного двумя окружностями с общим центром если радиусы равны 15 и 13.
Решение
Задача аналогична предыдущим.
S = pi (R^2 – r^2) = pi (15^2 – 13^2) = pi (225 – 169) = 56pi approx 175.92919 : см^2
Ответ: 56pi approx 175.92919 : см^2
Проверка .
Задача 4
Найдите площадь кольца ограниченного двумя окружностями с общим центром и радиусами 13 и 12 см.
Решение
Задача аналогична предыдущим.
S = pi (R^2 – r^2) = pi (13^2 – 12^2) = pi (169 – 144) = 25pi approx 78.53982 : см^2
Ответ: 25pi approx 78.53982 : см^2
Проверка .
Площадь кольца
Онлайн калькулятор
Площадь кольца по радиусам или диаметрам
 Чему равна площадь кольца ограниченного двумя окружностями, если:
Чему равна площадь кольца ограниченного двумя окружностями, если:
у внешней окружности
у внутренней окружности
Площадь кольца по толщине и любому другому параметру
 Чему равна площадь кольца ограниченного двумя окружностями, если:
Чему равна площадь кольца ограниченного двумя окружностями, если:
толщина кольца t =
Теория
Площадь кольца через радиусы
Чему равна площадь кольца S ограниченного двумя окружностями, если известны радиус внешней окружности R и радиус внутренней окружности r ?
Формула
Пример
К примеру, определим площадь кольца, у которого внешний радиус R = 3 см, а внутренний радиус r = 2 см:
S = 3.14 ⋅ (3² – 2²) = 3.14 ⋅ (9 – 4) = 3.14 ⋅ 5 = 15.7 см²
Ответ: S = 15.7 см²
Площадь кольца через диаметры
Чему равна площадь кольца S ограниченного двумя окружностями, если известны диаметр внешней окружности D и диаметр внутренней окружности d ?
Формула
Пример
К примеру, определим площадь шайбы, внешний диаметр которой D = 4 см, а внутренний – d = 2 см:
S = 3.14 / 4 ⋅ (4² – 2²) = 0.785 ⋅ (16 – 4) = 9.42 см²
Ответ: S = 9.42 см²
Площадь кольца через толщину
Чтобы посчитать площадь кольца S зная его толщину t, необходимо знать ещё какой-нибудь из следующих параметров:
- внешний диаметр D
- внутренний диаметр d
- радиус внешней окружности R
- радиус внутренней окружности r
Формулы
Пример
Для примера, найдём чему равна площадь кольца толщиной t = 2 см и внешним диаметром D = 5 см:
S = 3.14/4 ⋅ (5² – (5 – 2 ⋅ 2)²) = 0.785 ⋅ (25 – 1) = 18.84 см²
№ 54. Найдите площадь кругового кольца, заключенного между двумя окружностями с одним и тем же центром и радиусами: 1) 4 см и 6 см; 2) 5,5 ми 6,5 м; 3) а и b, а > b.
 Решебник по геометрии за 9 класс (А.В.Погорелов, 2001 год),
Решебник по геометрии за 9 класс (А.В.Погорелов, 2001 год),
задача №54
к главе «§14. Площади фигур».
Выделите её мышкой и нажмите CTRL + ENTER
Большое спасибо всем, кто помогает делать сайт лучше! =)
Нажмите на значок глаза возле рекламного блока, и блоки станут менее заметны. Работает до перезагрузки страницы.
Найдите площадь кругового кольца, заключенного между двумя концентрическими окружностями, длины которых равны а и b, где а < ; b?
Геометрия | 5 – 9 классы
Найдите площадь кругового кольца, заключенного между двумя концентрическими окружностями, длины которых равны а и b, где а < ; b.

Первая окружность с радиусом R₁
Длина окружности L = 2πR
b = 2πR₁⇒ R₁ = b / 2π
а = 2πR₂ ⇒ R₂ = а / 2π
Площадь окружности S = πR²
площадь кольца равна S₁ – S₂ = π(R₁² – R₂²) = π((b / 2π ) ² – (а / 2π)²) = (b² – а²) / 4π.

Найти площадь кругового сектра(кольца) заключенного между двумя окружностями, с одним и тем же центром и радиусом 4 и 6 см?
Найти площадь кругового сектра(кольца) заключенного между двумя окружностями, с одним и тем же центром и радиусом 4 и 6 см.
(подробно и с объяснением).

Площадь кругового кольца, находящегося между двумя окружностями с общим центром, равна 12дм², радиус одной окружности в 2 раза больше, чем радиус другой?
Площадь кругового кольца, находящегося между двумя окружностями с общим центром, равна 12дм², радиус одной окружности в 2 раза больше, чем радиус другой.
Найдите эти радиусы.

Даны две концентрические окружности, длина одной из них 33п см, а другой 27п см?
Даны две концентрические окружности, длина одной из них 33п см, а другой 27п см.
Найдите ширину кольца.

В кольце, образуемом двумя концентрическими окружностями, проведена хорда, касающаяся меньщей окружности?
В кольце, образуемом двумя концентрическими окружностями, проведена хорда, касающаяся меньщей окружности.
Найдите площадь кольца , если известно, что длина хорды равна 8 см.

Около правильного треугольника описана окружность и в него вписана окружность?
Около правильного треугольника описана окружность и в него вписана окружность.
Длина меньшей окружности равна 8пи.
Найдите площадь кольца и площадь треугольника.

Срочно?
№8. Радиусы двух концентрических окружностей относятся как 4 : 5.
Найдите их диаметры, если ширина кольца, образованного этими окружностями, равна 7 см.
№9. Найдите радиусы двух концентрических окружностей, если известно, что их диаметры относятся как 2 : 5 и ширина кольца, образованного этими окружностями, равна 24 см.

Помогите плииииииииииииииз?
От этой оценки зависит четвертная!
1. Фигура, ограниченная двумя концентрическими окружностями, называется кольцом, а разность радиусов данных окружностей – шириной этого кольца.
1) выразите ширину кольца через длины окружностей
2) радиусы окружностей равны 26см и 10см.
Найдите длину наибольшего отрезка, который целиком можно поместить в данное кольцо
Какую часть площади круга составляет площадь сектора, центральный угол которого равен 1)30°, 2)45°, 3)60°, 4)90°, 5)180°, 6)300°.

Площадь кругового кольца, заключенного между двумя окружностями с одним и тем же центром, равна 8 см2?
Площадь кругового кольца, заключенного между двумя окружностями с одним и тем же центром, равна 8 см2.
Найдите площади этих кругов, ограниченными этими окружностями, если радиус одной из них в три раза больше, чем радиус другой.

В правильный треугольник со стороной 4 см вписана окружность и около него описана окружность?
В правильный треугольник со стороной 4 см вписана окружность и около него описана окружность.
Найдите площадь кольца, заключенного между этими окружностями.

Ширина кольца, образованного концентрическими окружностями радиусов 3 см и 5 см, равна ?
Ширина кольца, образованного концентрическими окружностями радиусов 3 см и 5 см, равна :
На этой странице сайта размещен вопрос Найдите площадь кругового кольца, заключенного между двумя концентрическими окружностями, длины которых равны а и b, где а < ; b? из категории Геометрия с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 5 – 9 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.

МК||АС, АВ – секущая. По свойству углов, образованных при пересечении параллельных прямых секущей соответственные ∠ВМК = ∠ВАС = 80° MN – биссектриса, ∠ВМN = ∠KMN = 80° : 2 = 40° ВС – секущая при параллельных МК и АС. ⇒соответственные ∠ВКМ = ∠ВСА = ..

Ты знаешь чему равна длина отрезка ВС , и знаешь длина АС, и тут ты можешь так. BC – AC = BA 8 – 3 = 5.

З вeршини кута провeдeно промінь , пeрпeндикулярний до його бісeктриси , який утворює зі стороною даного кута гострий кут, градусна міра якого в 4 рази більша за даний кут . Знайдіть даний кут.

Площадь треугольника S = (a²·sinα) / 2, где а – боковая сторона, α – угол при вершине. A² = 2S / sinα = 2·48 / 0. 5 = 192, a = 8√3 см – это ответ.

Периметр прямоугольника рассчитывается по формуле : P = 2(a + b) Подставим значения a и b в формулу и получим : P = 2(10 + 8) = 36 см Ответ : 36 см.

Три прямые пересекаются в одной точке и образуют шесть углов. Найдите сумму трёх из этих углов, которые попарно не имеют общих точек.

Известно : биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим сторонам (в нашем случае – катетам), т. Е. дано отношение катетов 15 : 20 = 3 : 4 отношение катетов – – это тангенс острого угла в прямоугольном треугольнике и..
[spoiler title=”источники:”]
http://5terka.com/node/737
http://geometria.my-dict.ru/q/1739191_najdite-plosad-krugovogo-kolca-zaklucennogo-mezdu/
[/spoiler]
Площадь кольца
- Главная
- /
- Математика
- /
- Геометрия
- /
- Площадь кольца
Чтобы найти площадь кольца, ограниченного двумя концентрическими окружностями, воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Площадь кольца по радиусам или диаметрам

Чему равна площадь кольца ограниченного двумя окружностями, если:
у внешней окружности
=
у внутренней окружности
=
Ответ: S =
0
Округление числа π: Округление ответа:
Просто введите радиусы или диаметры окружностей, и получите ответ.
Площадь кольца по толщине и любому другому параметру

Чему равна площадь кольца ограниченного двумя окружностями, если:
толщина кольца t =
=
Ответ: S =
0
Округление числа π: Округление ответа:
Просто введите толщину кольца и любой другой известный вам параметр, и получите ответ.
Теория
Площадь кольца через радиусы
Чему равна площадь кольца S ограниченного двумя окружностями, если известны радиус внешней окружности R и радиус внутренней окружности r ?
Формула
S = π ⋅ (R² – r²)
Пример
К примеру, определим площадь кольца, у которого внешний радиус R = 3 см, а внутренний радиус r = 2 см:
S = 3.14 ⋅ (3² – 2²) = 3.14 ⋅ (9 – 4) = 3.14 ⋅ 5 = 15.7 см²
Ответ: S = 15.7 см²
Площадь кольца через диаметры
Чему равна площадь кольца S ограниченного двумя окружностями, если известны диаметр внешней окружности D и диаметр внутренней окружности d ?
Формула
S = π/4 ⋅ (D² – d²)
Пример
К примеру, определим площадь шайбы, внешний диаметр которой D = 4 см, а внутренний – d = 2 см:
S = 3.14 / 4 ⋅ (4² – 2²) = 0.785 ⋅ (16 – 4) = 9.42 см²
Ответ: S = 9.42 см²
Площадь кольца через толщину
Чтобы посчитать площадь кольца S зная его толщину t, необходимо знать ещё какой-нибудь из следующих параметров:
- внешний диаметр D
- внутренний диаметр d
- радиус внешней окружности R
- радиус внутренней окружности r
Формулы
S = π/4 ⋅ (D² – (D – 2t)²)
S = π/4 ⋅ ((d + 2t)² – d²)
S = π ⋅ (R² – (R – t)²)
S = π ⋅ ((r + t)² – r²)
Пример
Для примера, найдём чему равна площадь кольца толщиной t = 2 см и внешним диаметром D = 5 см:
S = 3.14/4 ⋅ (5² – (5 – 2 ⋅ 2)²) = 0.785 ⋅ (25 – 1) = 18.84 см²
См. также
Площадь кольца
 Чему равна площадь кольца ограниченного двумя окружностями, если:
Чему равна площадь кольца ограниченного двумя окружностями, если:
у внешней окружности
у внутренней окружности
Площадь кольца по толщине и любому другому параметру
 Чему равна площадь кольца ограниченного двумя окружностями, если:
Чему равна площадь кольца ограниченного двумя окружностями, если:
толщина кольца t =
Теория
Площадь кольца через радиусы
Чему равна площадь кольца S ограниченного двумя окружностями, если известны радиус внешней окружности R и радиус внутренней окружности r ?
Формула
Пример
К примеру, определим площадь кольца, у которого внешний радиус R = 3 см, а внутренний радиус r = 2 см:
S = 3.14 ⋅ (3² — 2²) = 3.14 ⋅ (9 — 4) = 3.14 ⋅ 5 = 15.7 см²
Ответ: S = 15.7 см²
Площадь кольца через диаметры
Чему равна площадь кольца S ограниченного двумя окружностями, если известны диаметр внешней окружности D и диаметр внутренней окружности d ?
Формула
Пример
К примеру, определим площадь шайбы, внешний диаметр которой D = 4 см, а внутренний – d = 2 см:
S = 3.14 / 4 ⋅ (4² — 2²) = 0.785 ⋅ (16 — 4) = 9.42 см²
Ответ: S = 9.42 см²
Площадь кольца через толщину
Чтобы посчитать площадь кольца S зная его толщину t, необходимо знать ещё какой-нибудь из следующих параметров:
- внешний диаметр D
- внутренний диаметр d
- радиус внешней окружности R
- радиус внутренней окружности r
Формулы
Пример
Для примера, найдём чему равна площадь кольца толщиной t = 2 см и внешним диаметром D = 5 см:
S = 3.14/4 ⋅ (5² — (5 — 2 ⋅ 2)²) = 0.785 ⋅ (25 — 1) = 18.84 см²
Как найти площадь кольца?
Плоская геометрическая фигура кольцо ограничена двумя окружностями, наружной и внутренней. Кольцо имеет наружный диаметр D и внутренний диаметр d. Площадь кольца будет равна разности между площадью большого и малого кругов. Площадь кольца

Кольцо представляет собой плоскую фигуру, образованную двумя окружностями (или кругами): внешней и внутренней. Это область, находящаяся между внешней и внутренней окружностью. Соответственно, его площадь будет определяться как разница между площадями внешнего и внутреннего кругов.
Sвнеш = пи*Rвнеш^2; Sвнутр = пи*Rвнутр^2, тогда площадь кольца равна:
Sкольца = Sвнеш — Sвнутр = пи*(Rвнеш^2 — Rвнутр^2). — Произведению разницы квадратов радиусов внешнего и внутреннего кругов на число пи.
где число пи = 3,14
Кольцо — это плоскость между двух окружностей с разными диаметрами и общим центром. Площадь кольца находится как разность между площадями большого (внешнего) и малого (внутреннего) круга.
Площадь кольца можно найти по разным формулам, в зависимости от заданных параметров.
Через радиусы внешний и внутренний;
где π — константа = 3,14. ,
R — внешний радиус кольца,
r — внутренний радиус кольца.
Через диаметры внешний и внутренний, из площади внешнего круга (через диаметр) вычитаем площадь внутреннего круга.
Через один из радиусов и толщину кольца.
Если известен внешний радиус, внутренний ищем вычитанием из него толщины кольца, r=R-k.
Если известен внутренний радиус, внешний ищем прибавлением к нему толщины кольца, R=r+k.
Площадь кольца
С помощью приведенных калькуляторов и формул можно рассчитать площадь кольца через радиусы или диаметры онлайн.
Формула площади кольца через радиус
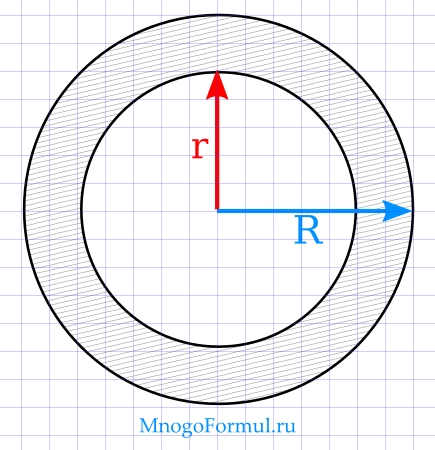
Чтобы найти площадь кольца,зная внутренний и внешний радиусы используют формулу:
, где R — внешний радиус кольца, r — внутренний радиус кольца.
Формула площади кольца через диаметр
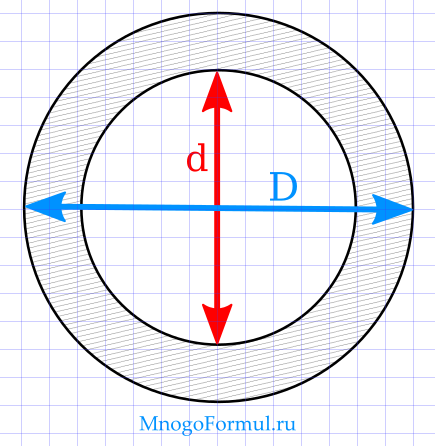
Чтобы найти площадь кольца,зная внутренний и внешний диаметры используют формулу:
cdot (D ^ 2-d^2)> , где D — внешний диаметр кольца, d — внутренний диаметр кольца.
Как рассчитать площадь кольца
На данной странице калькулятор поможет рассчитать площадь кольца онлайн. Для расчета задайте внутренние и внешние радиусы или диаметры.
Через радиусы
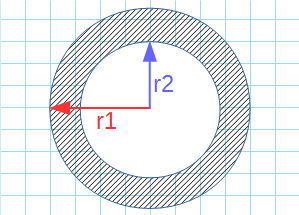
Формула для нахождения площади кольца через внешний и внутренний радиус:
π – константа равная (3.14); r1 – внешний радиус; r2 – внутренний радиус.
Через диаметры
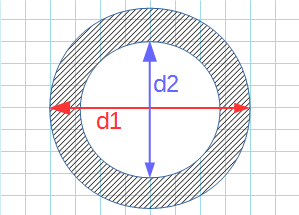
Формула для нахождения площади кольца через внешний и внутренний диаметр:
π – константа равная (3.14); d1 – внешний диаметр; d2 – внутренний диаметр.
