Как найти площадь кольца на квадратных клетках

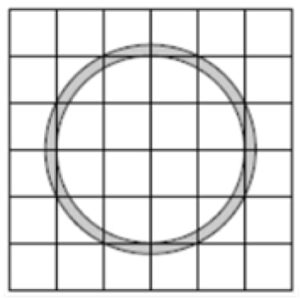
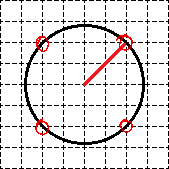
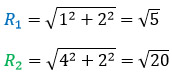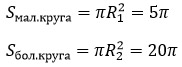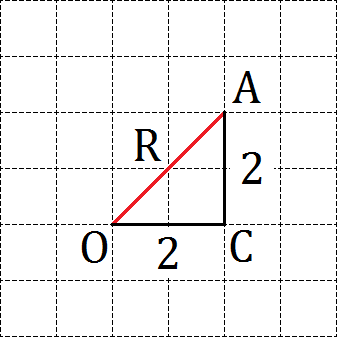Найдите площадь кольца ограниченного окружностями считая стороны клеток равными

Найдите площадь S круга, считая стороны квадратных клеток равными 1. В ответе укажите

Площадь круга определяется формулой Радиус окружности определяется из прямоугольного треугольника с катетами 2 и 1, тогда Поэтому

А нельзя ли как-нибудь обозначить прямоугольный треугольник, из которого нашли радиус? Я не могу увидеть его.

Как увидеть треугольник:

1. Найдите точку, в которой окружность пересекает узел сетки;

2. Прочертите линию от неё к центру;

3. Посмотрите, в какой прямоугольный треугольник входит эта линия в качестве гипотенузы.

Найдите площадь S кольца

Скачать
презентацию

Площадь >>

Задание: Найдите площадь S кольца, считая стороны квадратных клеток равными 1. В ответе укажите S/?.

Слайд 23 из презентации «Геометрические задачи в ЕГЭ». Размер архива с презентацией 2070 КБ.

Геометрия 11 класс

«Задачи на вычисление площади треугольника» – Проверка выполнения. Математический диктант. Девиз урока. Площадь. Площадь фигуры. Физкультминутка. Личностные цели. Вычислить площадь фигуры. Способы нахождения площади треугольника. Решение одной задачи. Выберите утверждение. Найти площадь фигуры. Айвен Нивен.

«Определение вектора в пространстве» – Задачи на компланарность. Правило многоугольника. Базисные задачи. Свойства скалярного произведения. Разложение векторов. Признак компланарности. Правило параллелограмма. Противоположно направленные векторы. Сонаправленные векторы. Коэффициенты разложения. Скалярное произведение. Вектор, проведенный в точку пересечения диагоналей параллелограмма. Определение компланарных векторов. Проверь себя. Сложение векторов.

«Векторы в пространстве» – Действия с векторами. Действие с векторами. Координаты вектора. Векторы являются некомпланарными. Векторы в пространстве. Разности. Умножение двух векторов. Разность двух векторов. Определение вектора. Правило многоугольника. Единственный вектор. Решение. Соноправленные векторы. Умение выполнять действия.

««Задачи по геометрии» 11 класс» – Основанием треугольной пирамиды является прямоугольный треугольник. Комбинация шара и усеченной пирамиды. Каким свойством должна обладать прямая призма. В правильную четырехугольную усеченную пирамиду можно вписать сферу. Технология проекта. Построим осевое сечение. Пирамида. В правильную четырехугольную усеченную пирамиду вписан шар. Около треугольной призмы описана сфера, центр которой лежит вне призмы.

«Формула объёма шара» – Находим выделенную часть. Проблемная задача. Найдите объем V части конуса. Объем искомой фигуры. В цилиндр вписан шар. Прямоугольный параллелепипед. Задачи. Рисунок на надгробной плите. Часть целого цилиндра. Найдите объем. Цилиндр. Архимед. Около шара описан цилиндр. Площадь поверхности шара. Интегральное исчисление. Объем шара. Название фигуры. Теорема. Шар и его части. Вывести формулу объема шара.

«Площадь сферы» – раза больше площади поверхности большого круга. Видно, что площадь поверхности шара в. Площадь поверхности шара радиусом. Центр шара (С). Площадь цилиндра, описанного вокруг шара радиусом. Расположенных на данном расстоянии (R). От данной точки (C). Около шара описан цилиндр, площадь поверхности которого равна 18. Слоя=vш.Сег.1-vш.Сег.2. И конуса. Найдем, что радиус такого шара. Шаровой сектор состоит из шарового сегмента.

Всего в теме «Геометрия 11 класс» 45 презентаций

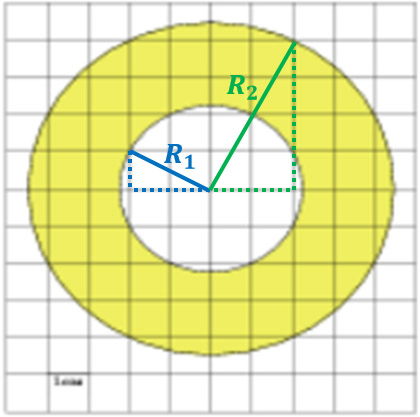
Решение №1315 Найдите площадь S (в см2) закрашенного кольца, изображенного на клетчатой бумаге.

Найдите площадь S (в см 2 ) закрашенного кольца, изображенного на клетчатой бумаге. Сторона клетки равна 1 см. В ответе укажите .

Источник задания: alexlarin.net

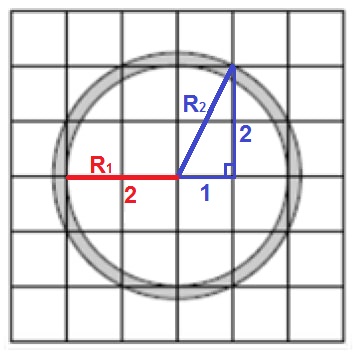
Площадь кольца это разность между площадью большого кольца и площадью маленького кольца.

Площадь круга находится по формуле S_⚫= πR 2 .
Радиус маленького круга R₁ = 2 см, найдём его площадь:

S_1⚫ = πR₁ 2 = π·2 2 = 4π см 2

Радиус большого круга найдём по теореме Пифагора из прямоугольного треугольника:

Площадь большого круга равна:

S_2⚫ = πR₂ 2 = π·√5 2 = 5π см 2

Площадь кольца равна:

S = S_2⚫ – S_1⚫ = 5π – 4π = π см 2

В ответе укажем :

[spoiler title=”источники:”]

http://5klass.net/geometrija-11-klass/Geometricheskie-zadachi-v-EGE/023-Najdite-ploschad-S-koltsa.html

[/spoiler]

На этой странице находится ответ на вопрос Найдите площадь кольца, считая стороны квадратных клеток равными 1, в ответе запишите s / п?, из категории
Геометрия, соответствующий программе для 10 – 11 классов. Чтобы посмотреть
другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов
подберите похожие вопросы и ответы в категории Геометрия. Ответ, полностью
соответствующий критериям вашего поиска, можно найти с помощью простого
интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе.
Обратите внимание на варианты ответов других пользователей, которые можно не
только просмотреть, но и прокомментировать.

Решение:

#799

3 октября 2013

Сегодня мы разберем нестандартную задачу B5 на площади из ЕГЭ по математике. В этой задаче требуется найти площадь закрашенного кольца, которое представляет собой две концентрические окружности разных радиусов:

Задача. Найдите площадь S закрашенного кольца, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см. В ответе укажите величину S/π.

Как и во всех задачах, для решения нам потребуется формула площади круга:

S = πR²

где R — радиус круга. Это стандартная формула, и ее обязательно надо знать. Но поскольку в задаче фигурируют два круга, то и радиусов будет два. Обозначим внутренний радиус (меньшей окружности) буквой R₁, а внешний радиус — R₂. Внутренний радиус очень легко считается, он равен двум клеточкам:

R₁ = 2 ⇒ R₁² = 4

Со вторым радиусом все сложнее. Окружность не проходит через «классические» точки горизонтальной и вертикальной осей, по которым обычно измеряется радиус. Однако на этой окружности есть другие точки, которые лежат в узлах исходной сетки. Отметим эти точки красным:

Что дают нам эти точки? Как минимум — визуальное представление того, как выглядит радиус. Для того, чтобы его вычислить, давайте отдельную сетку, на которой отметим центр окружности O и ту точку A на нашей окружности, в которую мы провели радиус. Затем достроим полученный отрезок до прямоугольного треугольника, двигаясь вдоль линий сетки. Получим треугольник OAC с прямым углом C:

По теореме Пифагора (квадрат гипотенузы равен сумме квадратов катетов) получаем:

R² = OA² = OC² + AC² = 2² + 2² = 4 + 4 = 8

Итого мы получили:

R₂² = 8

Теперь осталось найти площади внешнего и внутреннего кругов, образующих кольцо:

S₁ = πR₁² = π · 4 = 4π;
S₂ = πR₂² = π · 8 = 8π.

Поскольку закрашенное кольцо лежит между границами кругов, для нахождения его площади надо из площади большего круга S₂ вычесть площадь меньшего круга S₁. Получаем:

S = S₂ − S₁ = 8π − 4π = 4π

Но это еще не ответ! В задаче требуется найти величину S/π. Давайте сосчитаем:

S/π = 4π/π = 4

Вот мы и получили ответ! Как видите, ничего сверхъестественного в этой задаче нет. Достаточно помнить формулу площади круга, а также находить эту площадь через радиус, даже если этот радиус приходится считать через теорему Пифагора.

Надеюсь, этот урок сильно поможет тем, кто всерьез готовится к ЕГЭ по математике. Тем, кто не рассчитывает на то, что им попадутся легкие задачи (в частности, задача B5), а готовится решать в том числе и нестандартные примеры. В общем тренируйтесь — и обязательно сдадите экзамен на отличный балл.:)

Смотрите также:

1. Нестандартная задача B5 на площадь круга
2. Задача B5: площадь закрашенного сектора
3. Десятичные дроби
4. Специфика работы с логарифмами в задаче B15
5. Семинар: ЕГЭ по математике, задачи B3 на площади
6. Решение задач на движение по воде

Решение:

    Площадь кольца это разность между площадью большого кольца и площадью маленького кольца.

    Площадь круга находится по формуле S_⚫= πR².
    Радиус маленького круга R₁ = 2 см, найдём его площадь:

S_1⚫ = πR₁² = π·2² = 4π см²

    Радиус большого круга найдём по теореме Пифагора из прямоугольного треугольника:

R_{2}=sqrt{1^{2}+2^{2}}=sqrt{5}

    Площадь большого круга равна:

S_2⚫ = πR₂² = π·(√5)² = 5π см²

    Площадь кольца равна:

S = S_2⚫ – S_1⚫ = 5π – 4π = π см²

    В ответе укажем frac{S}{pi}:

frac{S}{pi}=frac{pi}{pi}=1

Ответ: 1.