Площадь кольца
- Главная
- /
- Математика
- /
- Геометрия
- /
- Площадь кольца
Чтобы найти площадь кольца, ограниченного двумя концентрическими окружностями, воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Площадь кольца по радиусам или диаметрам

Чему равна площадь кольца ограниченного двумя окружностями, если:
у внешней окружности
=
у внутренней окружности
=
Ответ: S =
0
Округление числа π: Округление ответа:
Просто введите радиусы или диаметры окружностей, и получите ответ.
Площадь кольца по толщине и любому другому параметру

Чему равна площадь кольца ограниченного двумя окружностями, если:
толщина кольца t =
=
Ответ: S =
0
Округление числа π: Округление ответа:
Просто введите толщину кольца и любой другой известный вам параметр, и получите ответ.
Теория
Площадь кольца через радиусы
Чему равна площадь кольца S ограниченного двумя окружностями, если известны радиус внешней окружности R и радиус внутренней окружности r ?
Формула
S = π ⋅ (R² – r²)
Пример
К примеру, определим площадь кольца, у которого внешний радиус R = 3 см, а внутренний радиус r = 2 см:
S = 3.14 ⋅ (3² – 2²) = 3.14 ⋅ (9 – 4) = 3.14 ⋅ 5 = 15.7 см²
Ответ: S = 15.7 см²
Площадь кольца через диаметры
Чему равна площадь кольца S ограниченного двумя окружностями, если известны диаметр внешней окружности D и диаметр внутренней окружности d ?
Формула
S = π/4 ⋅ (D² – d²)
Пример
К примеру, определим площадь шайбы, внешний диаметр которой D = 4 см, а внутренний – d = 2 см:
S = 3.14 / 4 ⋅ (4² – 2²) = 0.785 ⋅ (16 – 4) = 9.42 см²
Ответ: S = 9.42 см²
Площадь кольца через толщину
Чтобы посчитать площадь кольца S зная его толщину t, необходимо знать ещё какой-нибудь из следующих параметров:
- внешний диаметр D
- внутренний диаметр d
- радиус внешней окружности R
- радиус внутренней окружности r
Формулы
S = π/4 ⋅ (D² – (D – 2t)²)
S = π/4 ⋅ ((d + 2t)² – d²)
S = π ⋅ (R² – (R – t)²)
S = π ⋅ ((r + t)² – r²)
Пример
Для примера, найдём чему равна площадь кольца толщиной t = 2 см и внешним диаметром D = 5 см:
S = 3.14/4 ⋅ (5² – (5 – 2 ⋅ 2)²) = 0.785 ⋅ (25 – 1) = 18.84 см²
См. также

{S = pi (R^2 – r^2)}
С помощью приведенных калькулятора и формул можно рассчитать площадь кольца через радиусы или диаметры онлайн.
Кольцо — плоская геометрическая фигура, ограниченная двумя концентрическими окружностями.
Содержание:
- калькулятор площади кольца
- формула площади кольца через радиусы
- формула площади кольца через диаметры
- примеры задач
Формула площади кольца через радиусы
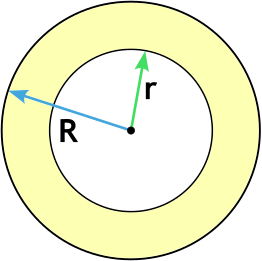
{S = pi (R^2 – r^2)}
R – внешний радиус кольца
r – внутренний радиус кольца
Формула площади кольца через диаметры
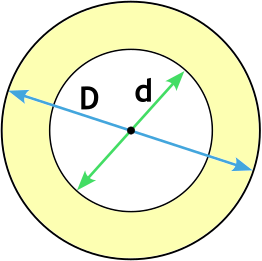
{S= dfrac{pi}{4}(D^2 – d^2)}
D – внешний диаметр кольца
d – внутренний диаметр кольца
Примеры задач на нахождение площади кольца
Задача 1
Найдите площадь кольца ограниченного двумя окружностями с общим центром и радиусами 3 см и 7 см.
Решение
В условии задачи даны радиусы ограничивающих кольцо окружностей, поэтому воспользуемся первой формулой.
S = pi (R^2 – r^2) = pi (7^2 – 3^2) = pi (49 – 9) = 40pi approx 125.66371 : см^2
Ответ: 108 cdot 0.866 approx 93.53074 : см^2
Полученный ответ можно проверить с помощью калькулятора .
Задача 2
Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны dfrac{4}{sqrt{pi}} и dfrac{2}{sqrt{pi}}.
Решение
Задача похожа на предыдущую, поэтому алгоритм ее решения будет тот же.
S = pi (R^2 – r^2) = pi ({Big(dfrac{4}{sqrt{pi}} Big) }^2 – {Big(dfrac{2}{sqrt{pi}} Big) }^2) = pi (dfrac{16}{pi} – dfrac{4}{pi}) = pi dfrac{12}{pi} = 12 : см^2
Ответ: 12 : см^2
Наш калькулятор может производить вычисления с выражениями. Для того, чтобы ввести радиусы из условия их нужно записать в понятном для калькулятора формате:
dfrac{4}{sqrt{pi}} : rarr : 4/sqrt(pi)
dfrac{2}{sqrt{pi}} : rarr : 2/sqrt(pi)
Если ввести данные в таком формате, можно проверить ответ .
Задача 3
Найдите площадь кольца образованного двумя окружностями с общим центром если радиусы равны 15 и 13.
Решение
Задача аналогична предыдущим.
S = pi (R^2 – r^2) = pi (15^2 – 13^2) = pi (225 – 169) = 56pi approx 175.92919 : см^2
Ответ: 56pi approx 175.92919 : см^2
Проверка .
Задача 4
Найдите площадь кольца ограниченного двумя окружностями с общим центром и радиусами 13 и 12 см.
Решение
Задача аналогична предыдущим.
S = pi (R^2 – r^2) = pi (13^2 – 12^2) = pi (169 – 144) = 25pi approx 78.53982 : см^2
Ответ: 25pi approx 78.53982 : см^2
Проверка .
Площадь кольца
Онлайн калькулятор
Площадь кольца по радиусам или диаметрам
 Чему равна площадь кольца ограниченного двумя окружностями, если:
Чему равна площадь кольца ограниченного двумя окружностями, если:
у внешней окружности
у внутренней окружности
Площадь кольца по толщине и любому другому параметру
 Чему равна площадь кольца ограниченного двумя окружностями, если:
Чему равна площадь кольца ограниченного двумя окружностями, если:
толщина кольца t =
Теория
Площадь кольца через радиусы
Чему равна площадь кольца S ограниченного двумя окружностями, если известны радиус внешней окружности R и радиус внутренней окружности r ?
Формула
Пример
К примеру, определим площадь кольца, у которого внешний радиус R = 3 см, а внутренний радиус r = 2 см:
S = 3.14 ⋅ (3² – 2²) = 3.14 ⋅ (9 – 4) = 3.14 ⋅ 5 = 15.7 см²
Ответ: S = 15.7 см²
Площадь кольца через диаметры
Чему равна площадь кольца S ограниченного двумя окружностями, если известны диаметр внешней окружности D и диаметр внутренней окружности d ?
Формула
Пример
К примеру, определим площадь шайбы, внешний диаметр которой D = 4 см, а внутренний – d = 2 см:
S = 3.14 / 4 ⋅ (4² – 2²) = 0.785 ⋅ (16 – 4) = 9.42 см²
Ответ: S = 9.42 см²
Площадь кольца через толщину
Чтобы посчитать площадь кольца S зная его толщину t, необходимо знать ещё какой-нибудь из следующих параметров:
- внешний диаметр D
- внутренний диаметр d
- радиус внешней окружности R
- радиус внутренней окружности r
Формулы
Пример
Для примера, найдём чему равна площадь кольца толщиной t = 2 см и внешним диаметром D = 5 см:
S = 3.14/4 ⋅ (5² – (5 – 2 ⋅ 2)²) = 0.785 ⋅ (25 – 1) = 18.84 см²
Найти площадь кольца образованного двумя окружностями
Площадь кольца
Онлайн калькулятор
Площадь кольца по радиусам или диаметрам
 Чему равна площадь кольца ограниченного двумя окружностями, если:
Чему равна площадь кольца ограниченного двумя окружностями, если:
у внешней окружности
у внутренней окружности
Площадь кольца по толщине и любому другому параметру
 Чему равна площадь кольца ограниченного двумя окружностями, если:
Чему равна площадь кольца ограниченного двумя окружностями, если:
толщина кольца t =
Теория
Площадь кольца через радиусы
Чему равна площадь кольца S ограниченного двумя окружностями, если известны радиус внешней окружности R и радиус внутренней окружности r ?
Формула
Пример
К примеру, определим площадь кольца, у которого внешний радиус R = 3 см, а внутренний радиус r = 2 см:
S = 3.14 ⋅ (3² — 2²) = 3.14 ⋅ (9 — 4) = 3.14 ⋅ 5 = 15.7 см²
Ответ: S = 15.7 см²
Площадь кольца через диаметры
Чему равна площадь кольца S ограниченного двумя окружностями, если известны диаметр внешней окружности D и диаметр внутренней окружности d ?
Формула
Пример
К примеру, определим площадь шайбы, внешний диаметр которой D = 4 см, а внутренний – d = 2 см:
S = 3.14 / 4 ⋅ (4² — 2²) = 0.785 ⋅ (16 — 4) = 9.42 см²
Ответ: S = 9.42 см²
Площадь кольца через толщину
Чтобы посчитать площадь кольца S зная его толщину t, необходимо знать ещё какой-нибудь из следующих параметров:
- внешний диаметр D
- внутренний диаметр d
- радиус внешней окружности R
- радиус внутренней окружности r
Формулы
Пример
Для примера, найдём чему равна площадь кольца толщиной t = 2 см и внешним диаметром D = 5 см:
S = 3.14/4 ⋅ (5² — (5 — 2 ⋅ 2)²) = 0.785 ⋅ (25 — 1) = 18.84 см²
Задача: определить площадь кольца, если известны радиусы
Условие задачи:
Две окружности, имеющие общий центр, образуют кольцо. Радиус внешней окружности равен 10 см, а внутренней 8 см. Найти площадь этого кольца.
Дано:
Радиус внешней окружности, R = 10 см
Радиус внутренней окружности, r = 8 см
Пояснение к рисунку:
O — общий центр окружностей
Найти площадь кольца: S
Площадь кольца можно выразить как разницу между площадями внешнего круга и внутреннего.
Формула площади внешнего круга.
Формула площади внутреннего круга.
После подстановки и преобразования, получаем следующее выражение для площади кольца.
Ответ:
Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14
Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами R1 и R2, R12
Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,900
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Задача: определить площадь кольца, если известны радиусы
Условие задачи:
Две окружности, имеющие общий центр, образуют кольцо. Радиус внешней окружности равен 10 см, а внутренней 8 см. Найти площадь этого кольца.
Дано:
Радиус внешней окружности, R = 10 см
Радиус внутренней окружности, r = 8 см
Пояснение к рисунку:
O – общий центр окружностей
Найти площадь кольца: S
Площадь кольца можно выразить как разницу между площадями внешнего круга и внутреннего.
Формула площади внешнего круга.
Формула площади внутреннего круга.
После подстановки и преобразования, получаем следующее выражение для площади кольца.
Ответ:
Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14
[spoiler title=”источники:”]
http://b4.cooksy.ru/articles/nayti-ploschad-koltsa-obrazovannogo-dvumya-okruzhnostyami
http://www-formula.ru/zadacha/solve-area-annulus-know-radius
[/spoiler]
![]()
Условие задачи:
Две окружности, имеющие общий центр, образуют кольцо. Радиус внешней окружности равен 10 см, а внутренней 8 см. Найти площадь этого кольца.
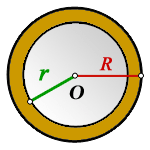
Дано:
Радиус внешней окружности, R = 10 см
Радиус внутренней окружности, r = 8 см
Пояснение к рисунку:
O – общий центр окружностей
Найти площадь кольца: S
Решение
Площадь кольца можно выразить как разницу между площадями внешнего круга и внутреннего.
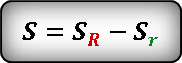
Формула площади внешнего круга.
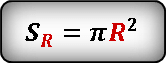
Формула площади внутреннего круга.
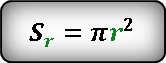
После подстановки и преобразования, получаем следующее выражение для площади кольца.
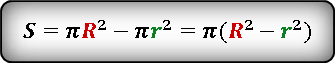
Вставляем значения.

Ответ:

![]() Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14
Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14
Калькулятор для расчета площади кольца
![]()
- Подробности
-
Опубликовано: 06 сентября 2017
-
Обновлено: 13 августа 2021
как найти площадь кольца
Ксения Владимировна
Ученик
(97),
закрыт
10 лет назад
Лучший ответ
Serg
Высший разум
(170536)
10 лет назад
По формуле S = П*(R^2 – r^2)
(Кольцо имеет 2 радиуса – внешний R и внутренний r)
Остальные ответы
Stas Garcia
Гуру
(2802)
10 лет назад
3.14 умножить на радиус кольца в квадрате.
Jonatan Barbara-Barbie
Ученик
(111)
7 лет назад
П*(R^2–r^2);
где:
R – Радиус большего круга
r – Радиус меньшего круга
П – Число Пи или 3.1415926535……
Похожие вопросы
