Решение:
Окружности нарисованы не очень удачно потому, что мы не можем с точностью сказать, какова длина у их радиусов. Придется искать.
Начертим радиусы этих двух окружностей так, как показано на рисунке, а затем сделаем еще одно дополнительное построение: достроим эти радиусы до прямоугольных треугольников.
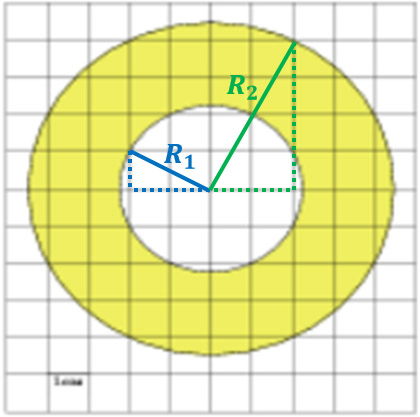
Теперь с помощью теоремы Пифагора можно найти длины радиусов.
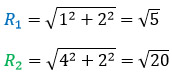
Далее найдем площадь маленького круга с радиусом R1 и большого круга с радиусом R2.
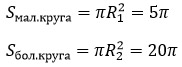
Чтобы найти площадь кольца надо из площади большого круга вычесть площадь маленького:
![]()
В ответе нас просят записать площадь, деленную на π, т.е. просто 15.
Ответ: 15.
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.
#799

СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика базового уровня
Математика базового уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Справочник
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
1 мая
Новый сервис: можно исправить ошибки!
29 апреля
Разместили актуальные шкалы ЕГЭ — 2023
24 апреля
Учителю: обновленный классный журнал
7 апреля
Новый сервис: ссылка, чтобы записаться к учителю
30 марта
Решения досрочных ЕГЭ по математике
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Поиск
?
было в ЕГЭ
в условии
в решении
в тексте к заданию
в атрибутах
Категория
Всего: 2 1–2
Добавить в вариант
Тип 12 № 245008 

i
Найдите (в см2) площадь S кольца, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). В ответе запишите
Аналоги к заданию № 245008: 263479 263419 263421 … Все
Решение
·
Помощь
Тип 12 № 263479 

Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). В ответе запишите
Аналоги к заданию № 245008: 263479 263419 263421 … Все
Решение
·
Прототип задания
·
Помощь
Всего: 2 1–2
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
3 октября 2013
Сегодня мы разберем нестандартную задачу B5 на площади из ЕГЭ по математике. В этой задаче требуется найти площадь закрашенного кольца, которое представляет собой две концентрические окружности разных радиусов:
Задача. Найдите площадь S закрашенного кольца, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см. В ответе укажите величину S/π.

Как и во всех задачах, для решения нам потребуется формула площади круга:
S = πR2
где R — радиус круга. Это стандартная формула, и ее обязательно надо знать. Но поскольку в задаче фигурируют два круга, то и радиусов будет два. Обозначим внутренний радиус (меньшей окружности) буквой R1, а внешний радиус — R2. Внутренний радиус очень легко считается, он равен двум клеточкам:
R1 = 2 ⇒ R12 = 4
Со вторым радиусом все сложнее. Окружность не проходит через «классические» точки горизонтальной и вертикальной осей, по которым обычно измеряется радиус. Однако на этой окружности есть другие точки, которые лежат в узлах исходной сетки. Отметим эти точки красным:
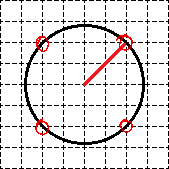
Что дают нам эти точки? Как минимум — визуальное представление того, как выглядит радиус. Для того, чтобы его вычислить, давайте отдельную сетку, на которой отметим центр окружности O и ту точку A на нашей окружности, в которую мы провели радиус. Затем достроим полученный отрезок до прямоугольного треугольника, двигаясь вдоль линий сетки. Получим треугольник OAC с прямым углом C:
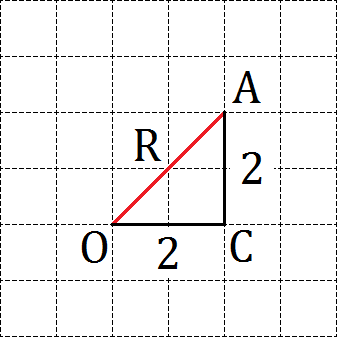
По теореме Пифагора (квадрат гипотенузы равен сумме квадратов катетов) получаем:
R2 = OA2 = OC2 + AC2 = 22 + 22 = 4 + 4 = 8
Итого мы получили:
R22 = 8
Теперь осталось найти площади внешнего и внутреннего кругов, образующих кольцо:
S1 = πR12 = π · 4 = 4π;
S2 = πR22 = π · 8 = 8π.
Поскольку закрашенное кольцо лежит между границами кругов, для нахождения его площади надо из площади большего круга S2 вычесть площадь меньшего круга S1. Получаем:
S = S2 − S1 = 8π − 4π = 4π
Но это еще не ответ! В задаче требуется найти величину S/π. Давайте сосчитаем:
S/π = 4π/π = 4
Вот мы и получили ответ! Как видите, ничего сверхъестественного в этой задаче нет. Достаточно помнить формулу площади круга, а также находить эту площадь через радиус, даже если этот радиус приходится считать через теорему Пифагора.
Надеюсь, этот урок сильно поможет тем, кто всерьез готовится к ЕГЭ по математике. Тем, кто не рассчитывает на то, что им попадутся легкие задачи (в частности, задача B5), а готовится решать в том числе и нестандартные примеры. В общем тренируйтесь — и обязательно сдадите экзамен на отличный балл.:)
Смотрите также:
- Нестандартная задача B5 на площадь круга

- Задача B5: площадь закрашенного сектора

- Десятичные дроби

- Специфика работы с логарифмами в задаче B15

- Семинар: ЕГЭ по математике, задачи B3 на площади

- Решение задач на движение по воде

![]()
Здравствуйте, друзья! В состав ЕГЭ по математике входят задачи связанные с нахождением площади круга или его частей (сектора, кольцевых элементов). Фигура задаётся на листе в клетку. В одних задачах масштаб клетки задаётся 1×1 сантиметр, в других он не оговаривается – даётся площадь элемента круга или самого круга.
Задания неглубокие, необходимо помнить формулу площади круга, уметь визуально (по клеткам) определить радиус круга, какую долю от круга составляет выделенный сектор. Кстати, на блоге имеется статья о площади сектора. Её содержание к решению представленных ниже задач отношения не имеет, но для тех, кто хочет вспомнить формулу площади круга и площади сектора будет весьма полезна. Рассмотрим задачи (взяты из открытого банка заданий):

Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см. В ответе запишите S/л.

Для того, чтобы площадь фигуры (кольца) необходимо из площади круга радиусом равным 2 вычесть площадь круга с радиусом 1. Формула площади круга:
![]()
Значит,
![]()
Разделим результат на число Пи и запишем ответ.
Ответ: 3

На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 51. Найдите площадь заштрихованной фигуры.

Площадь заштрихованной фигуры можно найти вычислив разность между площадью большего круга и площадью меньшего. Определим во сколько раз площадь большего отличается от площади меньшего. Пусть радиус меньшего равен R, тогда его площадь равна:
![]()
Радиус большего круга в два раза больше (видно по клеткам). Значит, его площадь равна:
![]()
Получили, что его площадь в 4 раза больше.
Следовательно, она равна 51∙4 = 204 см2
Таким образом, площадь заштрихованной фигуры равна 204 – 51 = 153 см2.
*Второй способ. Можно было вычислить радиус малого круга, затем определить радиус большего. Далее найти площадь большего и вычислить площадь искомой фигуры.

На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 1. Найдите площадь заштрихованной фигуры.

Данная задача по ходу решения практически не отличается от предыдущей, разница состоит лишь в том, что круги имеют разные центры.
Несмотря на то, что видно, что радиус большего круга в 2 раза больше радиуса меньшего, советую вам обозначить размер клетки переменной х (икс).
Так же, как и в предыдущей задаче, определим во сколько раз площадь большего отличается от площади меньшего. Выразим площадь меньшего круга, так как его радиус равен 3х:
![]()
Выразим площадь большего круга, так как его радиус равен 6х:
![]()
Как видно, площадь большего круга в 4 раза больше.
Следовательно, она равна 1∙4 = 4 см2
Таким образом, площадь заштрихованной фигуры равна 4 – 1 = 3 см2.
Ответ: 3

На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 9. Найдите площадь заштрихованной фигуры.

Обозначим размер клетки переменной х (икс).
Определим во сколько раз площадь большего круга отличается от площади меньшего. Выразим площадь меньшего круга. Так как его радиус равен 3∙х, то
![]()
Выразим площадь большего круга. Так как его радиус равен 4∙х, то
![]()
Разделим площадь большего на площадь меньшего:

То есть, площадь большего круга в 16/9 раза больше площади меньшего, следовательно, она равна:
![]()
Таким образом, площадь заштрихованной фигуры равна 16 – 9 = 7 см2.
*Второй способ.
Вычислим радиус меньшего круга. Его площадь равна 9, значит,

Найдём размер клетки и затем сможем определить радиус большего круга. Размер клетки равен:

Так как радиус большего круга соответствует 4 клеткам, то его радиус будет равен:

Определяем площадь большего круга:

Находим разность: 16 – 9 = 7 см2
Ответ: 7

На клетчатой бумаге нарисован круг площадью 48. Найдите площадь заштрихованного сектора.

В этой задаче очевидно, что заштрихованная часть составляет половину от площади всего круга, то есть равна 24.
Ответ: 24

На клетчатой бумаге изображён круг. Какова площадь круга, если площадь заштрихованного сектора равна 32?

По рисунку видно, что площадь сектора составляет треть от площади круга. Значит, площадь круга будет равна 32∙3 = 96.
Ответ: 96
![]()
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см. В ответе запишите S/л.

Посмотреть решение
Найдите площадь S круга, считая стороны квадратных клеток равными 1. В ответе укажите S/л.

Посмотреть решение
Небольшой итог.
В задачах связанных с площадью сектора круга необходимо уметь определять какую долю он составляет от площади круга. Это сделать не сложно, так как в подобных задачах центральный угол сектора кратен 30 либо 45.
В задачах связанных с нахождением площадей кольцевых элементов есть разные пути для решения, оба показаны в решённых заданиях. Способ, в котором размер клетки обозначается через переменную х, и затем определяются радиусы более универсален.
Но самое главное – не запоминать эти способы. Можно найти и третий и четвёртый путь решения. Главное – это знать формулу площади круга и уметь логически рассуждать.
На этом всё. Успеха вам!
С уважением, автор проекта Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
15
Способы вычисления площади на клетке
Выполнил:
ученик 7 «Б» класса
Растатуров Никита Сергеевич
Научный руководитель:
учитель математики
Растатурова Галина Владимировна
Архангельск
2017
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ…………………………………….……………………………………………….. 3
ГЛАВА 1. Из истории возникновения понятия «Площадь» ……………………………………….. 4
ГЛАВА 2. Способы вычисления площади фигуры на клетчатой бумаге………………………. 5
1.1. Три способа вычисления площади выпуклого многоугольника…..…………. ………… 5
1.2. Три способа вычисления площади невыпуклого многоугольника. ………………………. 6
1.3. Вычисление площади кольца по формуле Пика.…………………………………………… 6
1.4. Вычисление площади фигуры, используя карту произвольной местности по формуле Пика…………………………………………………………………………………………… 7
ГЛАВА 3 . Исследование, возможности использования способов вычисления площадей
фигур, изображенных на клетчатой поверхности………………………………………………8
3.1 Сравнительный анализ способов нахождения площади многоугольника на клетчатой
бумаге ……………..……………………………………………………………………………………. 8
3.2. Результаты эксперимента, проведенного в 7 “Б” классе …………………………………….9
ЗАКЛЮЧЕНИЕ.………………………………………………………………………….…….. 10
БИБЛИОГРАФИЧЕСКИЙ СПИСОК …….………………………………………….…….. …11
ПРИЛОЖЕНИЯ……………………………………………………………………………. … .12
ВВЕДЕНИЕ
“Математика учит точности мысли, подчинению
логике доказательства, понятию строго
обоснованной истины, а всё это формирует
личность, пожалуй, больше, чем музыка”.
Александр Данилович Александров
Впервые с проблемой вычисления площади фигур я столкнулся при решении различных задач, суть которых сводилась к тому, что требовалось найти площадь различных многоугольников, которых мы не рассматривали на уроках математики. Ведь до 7 класса мы знакомимся только с формулами для вычисления площади квадрата, прямоугольника и прямоугольного треугольника. Так как на уроке мы обычно выполняем решение в тетради, то я обратил внимание, что вычислить площадь того же квадрата помогают клетки, изображенные в тетради. Просматривая различную информацию в интернете, я натолкнулся на формулу, которая позволяет вычислить площадь фигуры, но только не по клеткам, а по их узлам. Впоследствии мне захотелось узнать, есть ли другие способы для вычисления площади различных фигур на клетчатой бумаге, какой из них проще, менее затратен по времени.
Гипотеза: если геометрическая фигура изображена на клетчатой бумаге, то ее площадь можно вычислить различными способами и убедиться, что результаты вычислений будут одинаковыми.
Актуальность выбранной темы: использование различных способов вычисления площади фигур на клетчатой бумаге усиливает интерес учащихся к математике и содействует развитию математических способностей школьников.
Цель работы: исследовать различные способы вычисления площадей фигур на клетчатой бумаге, сравнить полученные результаты.
Задачи исследования:
-
изучить литературу по исследуемой теме;
-
отобрать интересную и понятную информацию для исследования;
-
найти различные методы и приёмы вычисления площади фигур на клетчатой
бумаге.
-
провести сравнительный анализ “плюсов” и “минусов” найденных способов.
-
провести эксперимент в 6 «Б» классе об выявлении математических знаний
у учащихся при вычислении площади фигур;
-
проанализировать и систематизировать полученную информацию.
Объект исследования: задачи на вычисление площади различных фигур на клетчатой бумаге.
Предмет исследования: способы вычисления площади фигур на клетчатой бумаге.
Методы и исследования: моделирование, сравнение, обобщение, аналогии, анализ и классификация информации.
Практическая значимость исследования: результаты исследования могут быть использованы при решении задач в старших классах, а так же при подготовке ОГЭ и ЕГЭ.
ГЛАВА 1. Из истории возникновения понятия “Площадь”.
В повседневной жизни мы часто встречаемся с понятием площади. Мы говорим: площадь квартиры, площадь садового участка и т.д.
Необходимость в понятии «площадь» возникла из жизненных потребностей. В древности люди использовали для измерения длин те измерительные приборы, которые всегда были при себе.
Позже возникла потребность в измерении и сравнении разнообразных «фигур» (н.п. земельных участков). Было необходимо ввести величину, которая характеризовала бы величину той части плоскости, которую занимает фигура. Эту величину назвали площадью.
Измерение площадей является одним из самых древних разделов геометрии. В частности, название “геометрия” означает “землемерие”, т.е. связано именно с измерением площадей. Основы этой науки были заложены в Древнем Египте, где после каждого разлива Нила приходилось заново производить разметку участков, покрытых плодоносным илом, т. е. вычислять их площади.
Вавилоняне, так же как и египтяне измеряли большей частью простейшие фигуры, встречающиеся при межевании земель, возведении стен и насыпей, строительстве плотин и каналов и т.п.
Сохранилось немало планов земельных угодий, разделенных на прямоугольники, трапеции и треугольники, а также планов различных строений, свидетельствующих, что вавилонский землемер или архитектор должен был хорошо чертить и проводить геометрические расчеты.
Многие ученые решали проблему вычисления площади фигуры. В историю с понятием площади вошли имена Евклида, Архимеда, Пифагора, Герона Александрийского, Рене Декарта, Пьера Ферма, Георга Пика и др. Ими открыто большое количество различных формул и способов для вычисления площади фигуры.
ГЛАВА 2. Способы вычисления площади фигуры на клетчатой бумаге.
П ри изучении вычисления площадей многоугольников на клетчатой бумаге я заметил, что все задачи строятся на понятии узла. Узел напоминает узел в рыболовной сетке – пересечение горизонтальных и вертикальных линий. Все задачи достаточно разнообразны и занимательны, они заставляют думать, размышлять, анализировать, искать аналогии.
ри изучении вычисления площадей многоугольников на клетчатой бумаге я заметил, что все задачи строятся на понятии узла. Узел напоминает узел в рыболовной сетке – пересечение горизонтальных и вертикальных линий. Все задачи достаточно разнообразны и занимательны, они заставляют думать, размышлять, анализировать, искать аналогии.
Рассмотрим вычисление площади одной и той же фигуры тремя способами и сравним результат вычисления.
2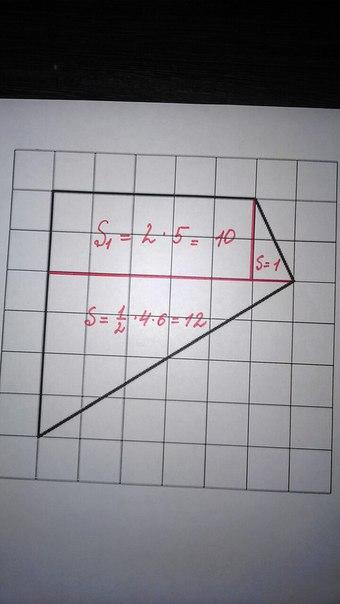 .1. Три способа вычисления площади выпуклого многоугольника.
.1. Три способа вычисления площади выпуклого многоугольника.
Разбиение. Смысл данного способа состоит в том, что многоугольник разрезается на прямоугольники и (или) прямоугольные треугольники с вершинами в узлах сетки.
Тогда площадь фигуры можно сосчитать по формуле:
Sф = S1 + S2 + S3 = 10 + 1 + 12 = 23.
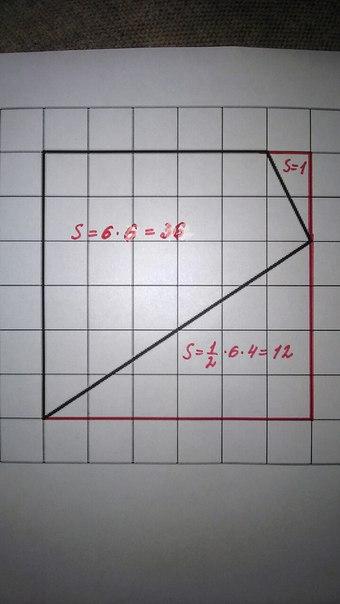
Дополнение до прямоугольника. Смысл данного способа – это дополнение многоугольника до прямоугольника так, чтобы его стороны проходили через вершины четырехугольника, а затем вычитание лишних частей. Получим, что площадь фигуры равна:
Sф = Sпр – (S1 + S2) = 36 – (1 + 12) = 23.
Ф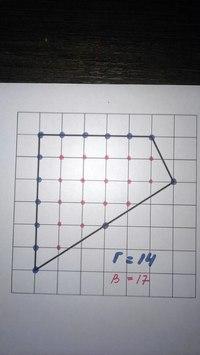 ормула Пика. Любая фигура изображенная на листе бумаги делит его на внутреннюю область и внешнюю, а еще есть граничные точки многоугольника. Нас интересуют внутренние узлы и узлы, которые лежат на границе многоугольника. Тогда формула выглядит так S = В + Г/2 – 1, где В – количество внутренних узлов, а Г – количество узлов на границе многоугольника.
ормула Пика. Любая фигура изображенная на листе бумаги делит его на внутреннюю область и внешнюю, а еще есть граничные точки многоугольника. Нас интересуют внутренние узлы и узлы, которые лежат на границе многоугольника. Тогда формула выглядит так S = В + Г/2 – 1, где В – количество внутренних узлов, а Г – количество узлов на границе многоугольника.
Эта формула получила название формула Пика в честь австрийского математика Георга Пика которая появилась в его восьмистраничной работе 1899 года, опубликованной в Праге.
Используя рисунок В= 17, Г = 14, получаем
S = 17 + 14/2 – 1 = 23.
Вычисляя площадь выпуклого многоугольника тремя способами, я получил один и тот же результат.
2.2. Три способа вычисления площади невыпуклого многоугольника.
Способ разбиения не подходит для данной фигуры, т.к. невозможно разбить ее на прямоугольники и (или) прямоугольные треугольники с вершинами в узлах сетки.
Д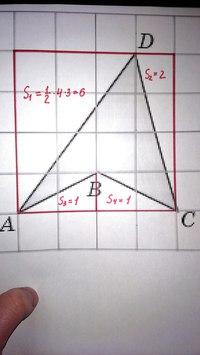 ополнение до прямоугольника.
ополнение до прямоугольника.
Достраивая многоугольник до прямоугольника, и отсекая лишние части, найдем площадь фигуры
Sф = S – (S1 + S2 + S3 + S4) = 42 – (6 + 2 + 1 + 1) = 16 – 10 = 6.
Ф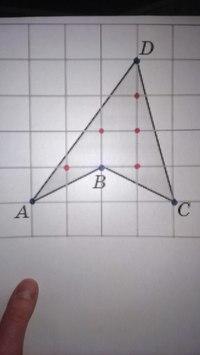 ормула Пика.
ормула Пика.
При подсчете внутренних узлов многоугольника и узлов, лежащих на границе получим, что
В = 5; Г = 4; S = 5 + 4/2 – 1 = 6.
И опять мы получили один и тот же результат.
2.3. Вычисление площади кольца по формуле Пика.
А если взять не многоугольник, а, например, кольцо и перенести его на клетчатую бумагу? Понятно, что первый и второй способы не удастся использовать. Применим формулу Пика и сравним полученный результат с результатом, полученным используя формулу для вычисления площади круга.
В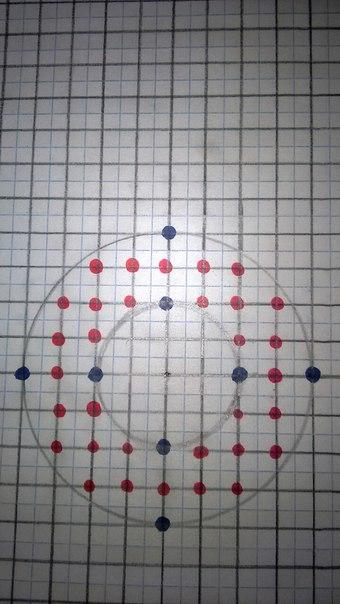 озьмем кольцо, которое построим с помощью двух окружностей с радиусами R=4 и r = 2.
озьмем кольцо, которое построим с помощью двух окружностей с радиусами R=4 и r = 2.
Вычислим площадь кольца с помощью формулы Пика:
В = 32, Г = 8, S= 32 + 4 – 1 = 35.
Вычислим площадь кольца по формуле площади круга, округлив число π до единиц.
S = πR2 – πr2 = 3* 16 – 3*4 = 48 – 12 = 36.
Округлим теперь π до десятых:
S = πR2 – πr2 = 3,1* 16 – 3,1*4 = 49,6 – 12,4 = 37,2.
А если округлить число π до сотых, то получим:
S = πR2 – πr2 = 3,14* 16 – 3,14*4 = 50, 24 – 12,56 = 37,68.
Сравнив результаты можно сделать вывод, что существует погрешность в вычислении площади по формуле Пика и чем точнее число π, тем она больше. Следовательно, данную формулу можно применять только для вычисления площадей многоугольников.
2.4. Вычисление площади фигуры, используя карту произвольной местности по формуле Пика.
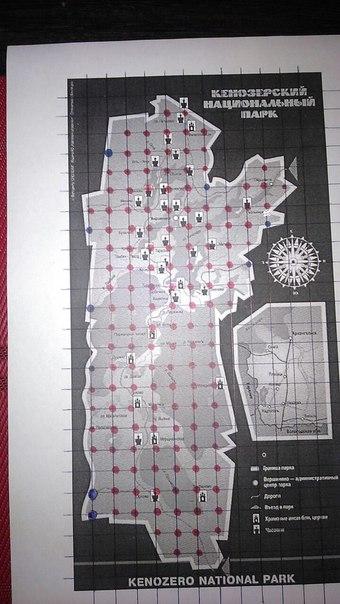
Если посмотреть на карту любой территории, то я заметил, что ее можно легко представить в виде многоугольника, перенести на клетчатую бумагу и сосчитать ее площадь. Для этого я в качестве примера выбрал Кенозерский национальный парк (Приложение 1).
Кенозерский национальный парк мне интересен не только своей необычайной красотой, но и тем, что моя мама и дедушка родились именно там. А так же в этом году 28 декабря национальный парк отпразднует свой юбилей. Ему исполнится 25 лет.
По конфигурации территория национального парка — вытянутый в меридиональном направлении многоугольник. Максимальное расстояние с юга на север — 72 км, с запада на восток — 27 км.
Площадь парка (из источника, взятого в сети Интернет) составляет 1 396 км2.
Я перенес карту парка на клетку и вычислил площадь, используя формулу Пика.
У меня получилось, что В = 144; Г = 9; S = 144 + 9/2 – 1 = 147,5.
На карте с юга на север максимум укладывается приблизительно 23,4 клетки.
Далее нашел сколько километров составляет сторона 1 клетки 72 : 23,4 = 3,08 км, значит площадь 1 клетки составляет 3,082 км2 = 9,4864 км2.
Вычислил площадь Кенозерского национального парка:
S = 147,5 * 9,4864 = 1399, 244 км2.
Погрешность получилась минимальная, следовательно, по формуле Пика легко и удобно по карте можно сосчитать площадь любой местности.
ГЛАВА 3 . Исследование возможности использования способов вычисления площадей фигур, изображенных на клетчатой поверхности.
3.1. Сравнительный анализ способов нахождения площади многоугольника на клетчатой бумаге.
1. Разбиение.
Этот способ прост в подсчёте площадей фигур, которые разбиваются на прямоугольники и (или) прямоугольные треугольники с вершинами в узлах сетки. К ним относятся выпуклые многоугольники.
К минусам можно отнести то, что в использовании этого способа приходится производить множество действий, а так же невозможность подсчёта площади фигур, которые не разбиваются на прямоугольники и (или) прямоугольные треугольники с вершинами в узлах сетки.
2. Дополнение до прямоугольника.
Этот способ так же прост в подсчёте при вычислении площади при небольшом количестве фигур, площадь которых необходимо отнять.
Минусы этого способа – сложность подсчёта площади многоугольников необычной
формы, большое количество фигур, площадь которых необходимо отнять, а так же невозможность подсчёта площади фигур, не относящихся к многоугольникам.
3. Формула Пика.
К плюсам я отнес то, что легко вычисляется площадь многоугольника с необычной формой, в отличие от предыдущих способов, краткость формулы, а так же возможность вычисления приближенного значения площади местности по карте, представив ее в виде многоугольника, перенеся ее на клетку.
Минусами этого способа считаю сложность вычисления площади фигуры с большим количеством узлов, а так же, если в фигуре есть «спорные» узлы (узлы, лежащие близко к стороне многоугольника). Вычисляя площадь фигур, не относящихся к многоугольникам, результат получается не точным.
3.2. Результаты эксперимента, проведенного в 7 “Б” классе.
Сделав сравнительный анализ, я провел эксперимент в своем классе с целью развития познавательной активности на уроках математики и выявления математических знаний у учащихся при вычислении площади фигур. Мной был проведен элемент урока в 6 “Б” классе. Я предложил своим одноклассникам вычислить площадь многоугольника тремя способами: “Разбиение”, Дополнение до прямоугольника” и по формуле Пика (Приложение 2).
Ребята с интересом отнеслись к моему заданию, но не у всех получились одинаковые результаты. Хотя формула Пика и легка при вычислении площади, у многих сложность возникла при нахождении узлов на границе фигуры и внутри нее. Так же у некоторых затруднение возникло при дополнении до прямоугольника. А вот “Разбиение” на прямоугольные треугольники и прямоугольники получилось у всех. Кстати, ребята так же обратили внимание, что способ разбиения невозможен при вычислении площади невыпуклого многоугольника, а вычисляя площадь невыпуклого многоугольника по формуле Пика ребята обнаружили «спорный узел».
ЗАКЛЮЧЕНИЕ
Изучив различные источники, выяснилось, что существует различные способы вычисления фигур по клеткам, но для меня были интересны и понятны три: разбиение, дополнение до прямоугольника и вычисления по формуле Пика.
Моя гипотеза – о том, что если геометрическая фигура изображена на клетчатой бумаге, то ее площадь можно вычислить различными способами и убедиться, что результаты вычислений будут одинаковыми, частично подтвердилась. Рассмотрев все три способа, я пришел к выводу, что не для всякой фигуры можно приметить каждый из них. У каждого из них есть свои плюсы и минусы.
Все три способа можно применить только для выпуклых многоугольников, перенеся их на клетчатую поверхность.
Формула Пика интересна своей простотой. И пусть она при вычислении площадей, не относящихся к многоугольникам, дает приближенное значение, можно легко оценить площадь той или иной территории на карте.
Проведя занятие в 7 “Б” классе я обратил внимание, что вычислять площадь многоугольников по клеткам ребятам интересно, но не хватает практики, одного занятия недостаточно. Нужно закреплять навык вычисления площадей. Думаю, что ребятам так же будет интересно попробовать вычислить площадь местности по карте.
Задачи на клетчатой бумаге встречаются в заданиях ЕГЭ и ОГЭ, поэтому я считаю, что такие задания нужно включать в элемент урока, так как это поможет им при подготовке к экзаменам.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК:
-
Атанасян Л. С. Геометрия 7-9, учебник. – М.Просвещение,2009.
-
Жарковская Н. М., Рисс Е. А. Геометрия клетчатой бумаги. Формула Пика // Математика, 2009, № 17, с. 24-25.
-
История математики с древнейших времен до начала XIX столетия, под редакцией Ю.П. Юшкевича., издательство Наука., М., 1970г
4. Смирнова И. М., Смирнов В. А. Геометрия на клетчатой бумаге. – М.: Чистые пруды, 2009.
Интернет ресурсы:
http://www.pppa.ru/additional/01geodesy/06/02topo.php
http://ru.wikihow.com http://knowledge.allbest.ru/mathematics/3c0b65635b3bd68b4c43b89521306d27_0.html
http://argonavt.narod.ru/Kenpark.html
http://infourok.ru/issledovatelskaya-rabota-vichislenie-ploschadi-mnogougolnika-na-kletchatoy-bumage-910671.html
https://docviewer.yandex.ru
Приложение 1.
Приложение 2
Разбиение Дополнение до прямоугольника
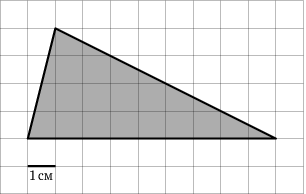

Формула Пика Разбиение

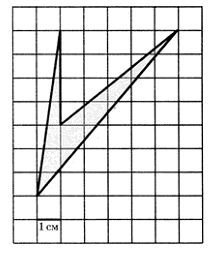
Дополнение до прямоугольника Формула Пика


Анкета.
1 Какой способ для вычисления площади фигуры по клеткам для тебя был проще и почему?
