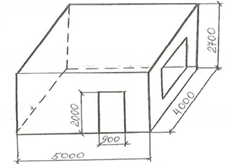
Как найти площадь комбинированные поверхности - Сайт, где вы сможете решить свои вопросы

8. Геометрия в пространстве (стереометрия)

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Задачи на комбинированные поверхности

В этой подтеме собраны поверхности являются комбинацией поверхностей, изученных ранее: пирамиды, призмы, конуса, цилиндра, сферы.

Для того, чтобы найти объем или площадь поверхности подобной комбинированной фигуры, нужно разбить ее на известные фигуры и искать объем/площадь по частям.

Рассмотрим пример:
Комбинация куба с ребром (a) и правильной четырехугольной пирамиды с высотой (a):

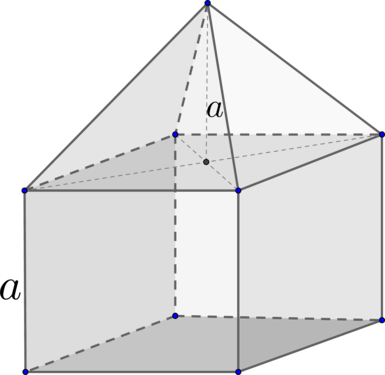
Объем такой фигуры равен (V=V_{text{куб}}+V_{text{пирамида}}=a^3+dfrac13a^2cdot
a=dfrac43a^3)

Задание
1

#2957

Уровень задания: Равен ЕГЭ

Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).

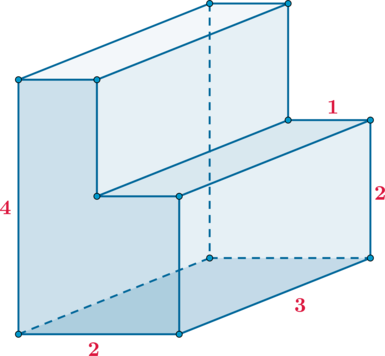
Заметим, что можно разбить данный многогранник на два непересекающихся прямоугольных параллелепипеда (ABCDA_1B_1C_1D_1) и (DCEFD_2C_2E_1F_1):

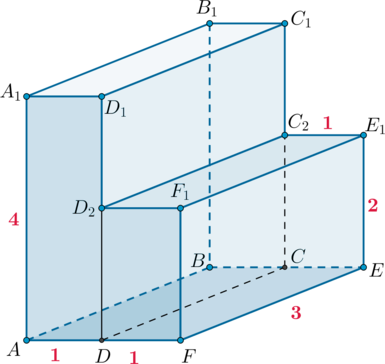
Тогда объем первого параллелепипеда будет равен (1cdot 3cdot
4=12), а объем второго (1cdot 3cdot 2=6). Следовательно, объем всего многогранника будет равен (12+6=18).

Ответ: 18

Задание
2

#1376

Уровень задания: Сложнее ЕГЭ

Точка (A) – середина оси цилиндра, высота которого (h). Точка (B) лежит на основании цилиндра (с центром (O) и радиусом (R)), причём угол между (AB) и плоскостью основания равен (60^circ), Объём заштрихованной области [V_{text{штрих}} = dfrac{75sqrt{5}}{sqrt{pi}}.] Найдите площадь боковой поверхности конуса с вершиной (A) и основанием, совпадающим с основанием цилиндра.

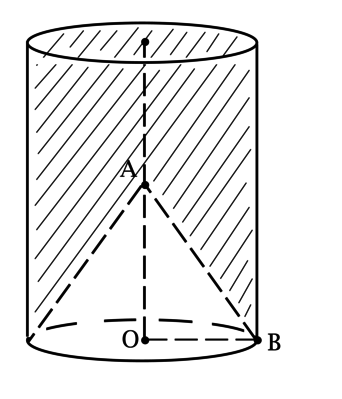
Рассмотрим прямоугольный треугольник (AOB): (AO = 0,5h), (angle ABO = 60^circ), (OB = R), тогда (0,5h = Rcdot mathrm{tg}, 60^circ = Rsqrt{3}), откуда (h = 2Rsqrt{3}); (AB = dfrac{R}{cos 60^circ} = 2 R).

[dfrac{75sqrt{5}}{sqrt{pi}} = V_{text{штрих}} = V_{text{цил}} – V_{text{кон}} = pi R^2 h – dfrac{1}{3}pi R^2cdot 0,5 h = pi R^2cdotdfrac{5h}{6} = pi R^3dfrac{5sqrt{3}}{3},] тогда (dfrac{75sqrt{5}}{sqrt{pi}} = pi R^3dfrac{5sqrt{3}}{3}), откуда (R = sqrt{dfrac{15}{pi}}), тогда [S_{text{бок кон}} = pi Rcdot AB = 2pi R^2 = 30.]

Ответ: 30

Задание
3

#1885

Уровень задания: Сложнее ЕГЭ

Верхняя грань куба является основанием пирамиды, высота которой равна (4). Найдите площадь поверхности фигуры, если сторона квадрата равна (6).

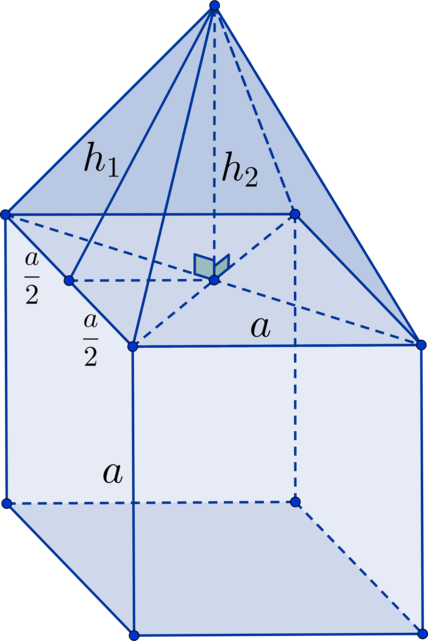
Найдем сперва апофему пирамиды (h_1) из прямоугольного треугольника, в котором она является гипотенузой, а катеты – это высота пирамиды (h_2) и половина стороны квадрата (displaystyle frac{a}{2}): (displaystyle h_1^2 = h_2^2 + frac{a^2}{4}) (Rightarrow) (displaystyle h_1^2 = 16 + frac{36}{4}) (Rightarrow) (h_1 = 5). Площадь боковой грани пирамиды: (displaystyle frac{1}{2}ah_1 = frac{1}{2}cdot6cdot5 = 15). Площадь грани куба: (a^2 = 36). Площадь поверхности фигуры состоит из пяти граней куба и четырех боковых граней пирамиды: (S = 5cdot36 + 4cdot15 = 180 + 60 = 240).

Ответ: 240

Задание
4

#1884

Уровень задания: Сложнее ЕГЭ

Песочные часы состоят из двух одинаковых усеченных конусов, плоскости оснований которых параллельны. Высота песочных часов (H = 16). Радиус окружности, являющейся пересечением боковых поверхностей конусов, равен (1). Тангенс половины угла раствора каждого конуса равен (frac{1}{2}). Найдите объем песочных часов (V), умноженный на (frac{3}{pi}).

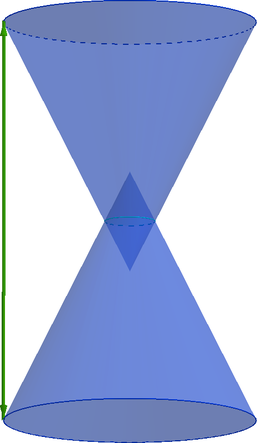
Выберем какое-нибудь сечение конусов плоскостью (alpha), проходящей через их общую ось вращения.

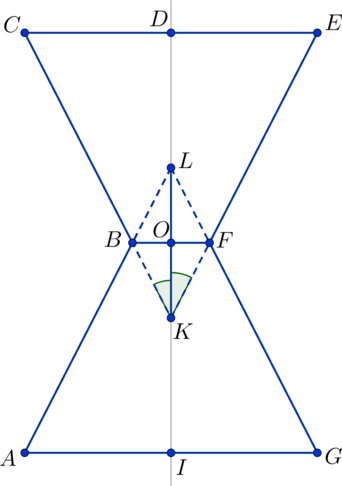
На рисунке в плоскости (alpha): (DI) – ось вращения конусов, отрезок (DI) совпадает с высотой песочных часов и равен (16). Отрезки (CD) и (DE) являются радиусами окружности, лежащей в верхнем основании фигуры, а отрезки (BO) и (OF) являются радиусами окружности пересечения конусов, поэтому (BO = OF = 1). Угол раствора конуса (angle CKE) делится пополам осью вращения на равные углы (angle CKD) и (angle DKE), поэтому (mathrm{tg}, angle CKD = mathrm{tg}, angle DKE = frac{1}{2}). Рассмотрим (triangle CKD) и (triangle BKO). Плоскости оснований конусов и плоскость, содержащая окружность пересечения конусов, параллельны друг другу (Rightarrow) рассматриваемая плоскость сечения (alpha) будет пересекать эти плоскости по прямым, параллельным друг другу (Rightarrow) (CD || BO) (Rightarrow) (triangle CKD) и (triangle BKO) подобны друг другу (Rightarrow) (frac{CD}{BO} = frac{KD}{KO}). Ось вращения перпендикулярна плоскостям оснований и плоскости пересечения конусов (Rightarrow) (triangle CKD) и (triangle BKO) – прямоугольные треугольники. Т.к. (DI = H) (Rightarrow) (DO = OI = H:2 = 8); (KO = BO:mathrm{tg},angle CKD = 1:frac{1}{2} = 2) (Rightarrow) (KD = KO + OD = 2 + 8 = 10) (Rightarrow) (frac{CD}{BO} = frac{KD}{KO} = frac{10}{2} = 5) (Rightarrow) (CD = 5).

Объем усеченного конуса (CBOFEDC) можно посчитать как разность объемов конуса (KCDE) и конуса (KBOF): [V_{CBOFEDC} = V_{KCDE} – V_{KBOF} = frac{1}{3}cdotpi CD^2cdot KD – frac{1}{3}cdotpi BO^2cdot KO = frac{1}{3}cdotpicdot 5^2cdot 10 – frac{1}{3}cdotpicdot 1^2cdot 2 = frac{248pi}{3}.]

Объем песочных часов складывается из двух объемов усеченного конуса, т.к. ситуация с нижним конусом полностью аналогична ситуации с верхним конусом в силу симметрии задачи, поэтому их объемы совпадают (CBOFEDC) объем песочных часов равен (2cdotfrac{248pi}{3}). Окончательно, после умножения на (frac{3}{pi}) получаем: [V = 496.]

Ответ: 496

Задание
5

#4022

Уровень задания: Легче ЕГЭ

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Найдем площадь поверхности большого прямоугольного параллелепипеда. Он имеет две грани с площадью (4cdot 5), две грани с площадью (4cdot 2) и две грани с площадью (2cdot 5). Следовательно, площадь его поверхности равна (2(4cdot 5+4cdot 2+2cdot 5)=76).
Из этого параллелепипеда вырезали прямоугольный параллелепипед с ребрами 1, 1 и 2. В результате этого площадь боковой поверхности уменьшилась на (2cdot (1cdot 1)) и увеличилась на (4cdot (1cdot
2)). Следовательно, площадь поверхности многогранника, изображенного на рисунке, равна [76-2+8=82]

Ответ:

Многолетняя практика подтверждает тот факт, что задачи ЕГЭ на комбинированные поверхности вызывают у выпускников определенные затруднения. При этом подобные задания из раздела «Геометрия в пространстве» включаются в программу аттестационного испытания по математике из года в год. В связи с этим вспомнить базовые алгоритмы выполнения подобных задач просто необходимо.

Как подготовиться к экзамену?

Хотите решать геометрические задачи по теме «Комбинированные поверхности», не допуская ошибок? Для этого достаточно усвоить несложный алгоритм нахождения правильного ответа.

Для вычисления объема, площади или других неизвестных параметров комбинированной фигуры необходимо прежде всего поделить ее на известные элементы.
Затем рекомендуем вспомнить основные формулы получившихся фигур.
Освежив в памяти эту информацию и правильно применив ее, вы сможете рассчитать искомый параметр.

Чтобы подготовка к сдаче единого государственного экзамена была действительно качественной и эффективной, занимайтесь вместе с математическим порталом «Школково». Для того чтобы задачи ЕГЭ по теме «Комбинированные фигуры» не вызывали у старшеклассников особых затруднений, вначале им непременно стоит освежить в памяти базовый теоретический материал. Причем для этого вовсе не обязательно искать нужный параграф в школьном учебнике. Весь необходимый материал уже собран и понятно изложен в разделе «Теоретическая справка».

Чтобы применить полученные знания на практике, предлагаем выпускникам попрактиковаться в выполнении онлайн-задач, например, на тему «Вписанные и описанные поверхности». Чтобы найти соответствующие упражнения, достаточно перейти в раздел «Каталог». База заданий регулярно дополняется. Для каждого упражнения на сайте мы прописали алгоритм решения и правильный ответ.

Чтобы в случае необходимости быстро найти задание, вы можете сохранить его в разделе «Избранное». Это позволит вам в любой момент вернуться к нему и обсудить принцип его выполнения со школьным учителем или репетитором.

УСТАЛ? Просто отдохни

Источник

Тема 2.

Геометрия в пространстве (стереометрия)

Комбинированные тела: их объемы и площади поверхностей

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами – ЛЕГКО!

Подтемы раздела

геометрия в пространстве (стереометрия)

Решаем задачи

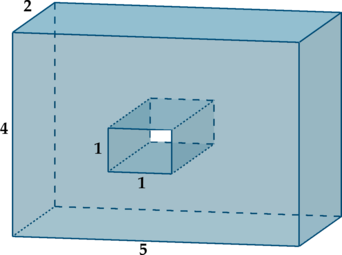
Найдите объём фигуры, получившейся после удаления маленького прямоугольного параллелепипеда из
большого.

Показать ответ и решение

Объём оставшейся фигуры равен разности объёмов большого прямоугольного параллелепипеда (каким
он был до удаления) и маленького (удалённого).

Таким образом, искомый объём равен

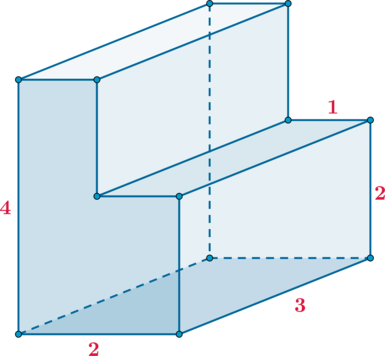
Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника
прямые).

Показать ответ и решение

Заметим, что можно разбить данный многогранник на два непересекающихся прямоугольных
параллелепипеда и :

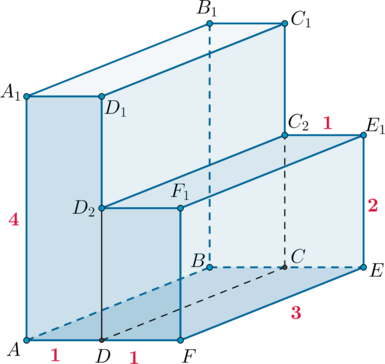
Тогда объем первого параллелепипеда будет равен , а объем второго .
Следовательно, объем всего многогранника будет равен .

Из единичного куба вырезана правильная четырёхугольная призма со стороной
основания 0,6 и боковым ребром . Найдите площадь поверхности
оставшейся части куба.

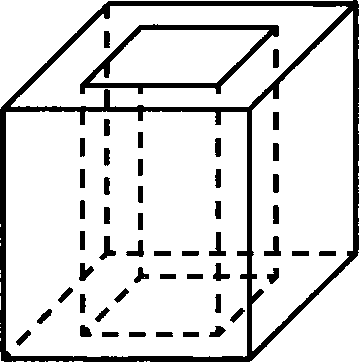
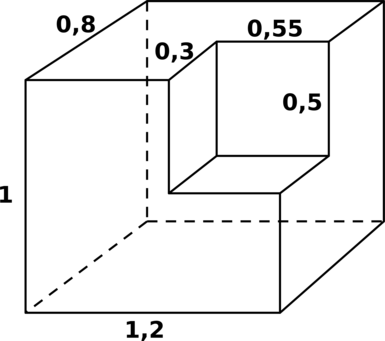
Из единичного куба вырезана правильная четырёхугольная призма со стороной
основания 0,6 и боковым ребром 1. При этом центры нижних оснований
призмы и куба совпадают. Найдите площадь поверхности оставшейся части
куба.

Показать ответ и решение

Сначала вычислим площадь поверхности куба с ребром 1. Если —
площадь одной грани куба, то .
Найдем и вычтем площади верхнего и нижнего оснований призмы:

Найдем и прибавим площади боковых граней призмы:

Тогда площадь поверхности оставшейся части куба равна 7,68.

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

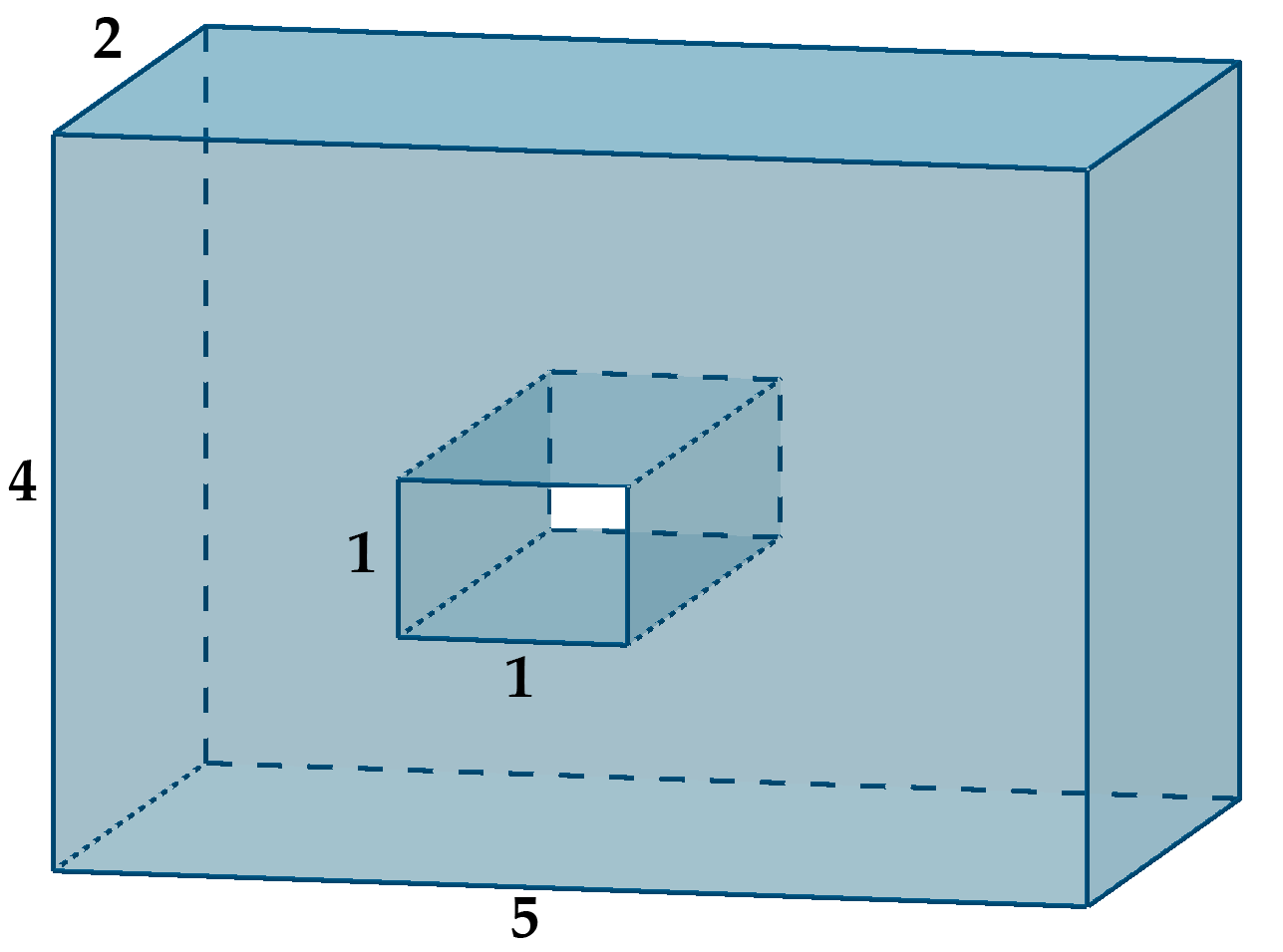
Показать ответ и решение

Найдем площадь поверхности большого прямоугольного параллелепипеда. Он имеет две грани с площадью 4 ⋅5, две грани с
площадью 4⋅2 и две грани с площадью 2⋅5. Следовательно, площадь его поверхности равна

Из этого параллелепипеда вырезали прямоугольный параллелепипед с ребрами 1, 1 и 2. В результате этого площадь боковой
поверхности уменьшилась на и увеличилась на Следовательно, площадь поверхности многогранника,
изображенного на рисунке, равна

Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,6 и боковым ребром 1. Найдите
площадь поверхности оставшейся части куба.

Показать ответ и решение

Площадь поверхности равна сумме четырёх «внешних» вертикальных граней, оставшихся частей двух горизонтальных граней и
четырёх «внутренних» горизонтальных граней, то есть

Песочные часы состоят из двух одинаковых усеченных конусов, плоскости оснований которых
параллельны. Высота песочных часов H = 16 . Радиус окружности, являющейся пересечением боковых
поверхностей конусов, равен . Тангенс половины угла раствора каждого конуса равен 1
2 . Найдите
объем песочных часов , умноженный на 3
π .

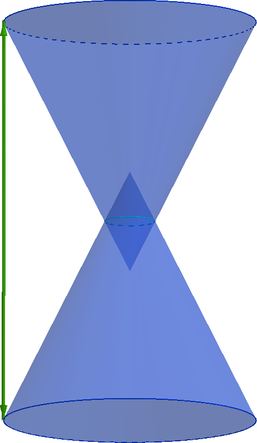
Показать ответ и решение

Выберем какое-нибудь сечение конусов плоскостью , проходящей через их общую ось
вращения.

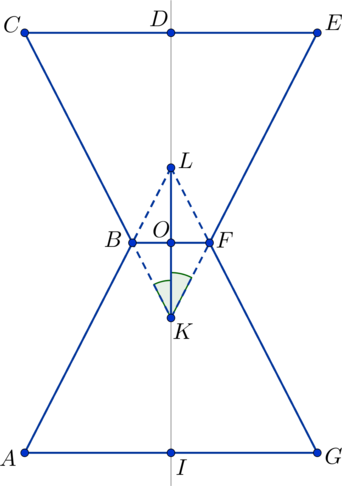
На рисунке в плоскости : – ось вращения конусов, отрезок совпадает с высотой
песочных часов и равен . Отрезки и являются радиусами окружности, лежащей в
верхнем основании фигуры, а отрезки и являются радиусами окружности пересечения
конусов, поэтому . Угол раствора конуса ∠CKE делится пополам осью вращения на
равные углы ∠CKD и ∠DKE , поэтому . Рассмотрим △CKD и △BKO .
Плоскости оснований конусов и плоскость, содержащая окружность пересечения конусов, параллельны
друг другу рассматриваемая плоскость сечения будет пересекать эти плоскости по прямым,
параллельным друг другу CD ||BO △CKD и △BKO подобны друг другу CD- KD-
BO = KO .
Ось вращения перпендикулярна плоскостям оснований и плоскости пересечения конусов
△CKD и △BKO – прямоугольные треугольники. Т.к. DI = H ;
CD-= KD- = 10 = 5
BO KO 2
CD = 5 .

Объем усеченного конуса можно посчитать как разность объемов конуса KCDE и
конуса KBOF :

Объем песочных часов складывается из двух объемов усеченного конуса, т.к. ситуация с нижним
конусом полностью аналогична ситуации с верхним конусом в силу симметрии задачи, поэтому их
объемы совпадают объем песочных часов равен 248π-
2 ⋅ 3 . Окончательно, после умножения
на получаем:

Верхняя грань куба является основанием пирамиды, высота которой равна . Найдите площадь
поверхности фигуры, если сторона квадрата равна .

Источник

Описание презентации по отдельным слайдам:

1 слайд

Наглядная геометрия
Площади
комбинированных
фигур
Красовская Варвара Сергеевна
МБОУ СОШ № 35 г. Шахты Ростовской обл.
6 класс.
2 слайд

Практическая работа
№1
Найти площади фигур,
выполнив необходимые измерения
Фигуры
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
0 1 2 3 4 5 6 7 8 9 10 11
3 слайд

Подсказка (3)
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
0 1 2 3 4 5 6 7 8 9 10 11
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
0 1 2 3 4 5 6 7 8 9 10 11
S1
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
0 1 2 3 4 5 6 7 8 9 10 11
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
0 1 2 3 4 5 6 7 8 9 10 11
S2
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
0 1 2 3 4 5 6 7 8 9 10 11
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
0 1 2 3 4 5 6 7 8 9 10 11
S3
4 слайд

Решение задач
№1-1
Вычислить площадь закрашенной фигуры.
Нет ли здесь лишних данных?
Ответ
40
30
25
12
6
820
5 слайд

Решение задач
№2
Вычислить площадь закрашенной фигуры.
Нет ли здесь лишних данных?
Ответ
78
40
64
38
688
6 слайд

№3
Какова площадь заштрихованной части?
Ответ
Решение задач
20
11
20
11
220
220 : 2 · 3 = 330
7 слайд

№4
Вычислить площадь треугольника.
Придумать способ вычисления площади
прямоугольного треугольника.
Ответ (3)
Решение задач
а
b
S = а · b
S∆ = а · b : 2
8 слайд

№5
Найдите площадь треугольника, если
площадь каждой клетки 1 см2?
Решение задач
Ответ
9 слайд

1
6 · 8 = 48
2
2 · 8 : 2 = 8
3
4 · 6 : 2 = 12
4
2 · 6 : 2 = 6
S∆ = 48 – 8 – 12 – 6
S∆ = 22
10 слайд

№6
Начертите прямоугольник со сторонами
9 см и 4 см. Вырежьте его. Затем разрежьте
этот прямоугольник на 3 прямоугольника
так, чтобы из них можно было составить
квадрат.
Решение задач
Ответ
12 слайд

Практическая работа
№2
На рисунке изображён параллелограмм
(четырёхугольник, противоположные
Стороны которого попарно параллельны).
Вычислите его площадь, если АD = 3 см, ВК = 2 см
Решение
А
В
С
D
K
13 слайд

А
В
С
D
K
Подсказка (4)
M
S1
S2
S = S1 + S2
S = 2 + 4
= 6 (см2)
14 слайд

В
А
K
С
D
Подсказка (4)
S1
S1 : 2
S2
S2 : 2
S3
S = S1 : 2 + S2 : 2 + S3
S = 2 + 1 + 4
= 7
15 слайд

Практическая работа
№3
Найдите площади четырёхугольников,
изображённых на рисунке.
Ответ (2)
А
K
D
В
С
M
N
Р
3 см
3 см
5 см
2 см
2 см
4 см
2 см
8 см2
15 см2
16 слайд

Методическое пособие
Введение в геометрию. 6 класс: планирование, конспекты
занятий / авт.-сост. И.В.Фотина. – Волгоград: Учитель, 2010.
http://etftrends.typepad.com/photos/uncategorized/2008/04/30/scissors_2.png
Ножницы:
Анимация и презентации:
Каратанова Марина Николаевна МКОУ СОШ №256 ГО ЗАТО г.Фокино Приморский край
17 слайд

Интернет-ресурсы:
Школьный клипарт http://s3.pic4you.ru/allimage/y2013/10-24/12216/3925122.png
Линейки http://s1.pic4you.ru/allimage/y2012/08-20/12216/2356205.png
Лист в клеточку http://s1.pic4you.ru/allimage/y2012/08-20/12216/2356208.png
Скрепка http://img-fotki.yandex.ru/get/6610/134091466.1c/0_8f975_cc74afe5_S
Циркуль http://img-fotki.yandex.ru/get/6521/108950446.113/0_cd1e6_7c1b8dea_S

Источник

A combined figure is a geometrical shape that is the combination of many simple geometrical shapes.

To find the area of combined figures we will follow the steps:

Step I: First we divide the combined figure into its simple geometrical shapes.

Step II: Then calculate the area of these simple geometrical shapes separately,

Step III: Finally, to find the required area of the combined figure we need to add or subtract these areas.

Solved Examples on Area of combined figures:

1. Find the area of the shaded region of the adjoining figure. (Use π = (frac{22}{7}))

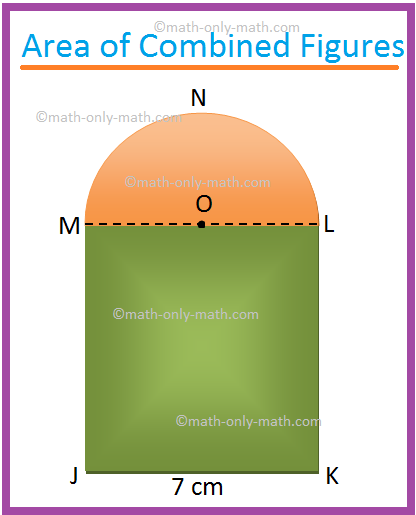
JKLM is a square of side 7 cm. O is the centre of the
semicircle MNL.

Solution:

Step I: First we divide the combined figure into
its simple geometrical shapes.

The given combined shape is combination of a
square and a semicircle.

Step II: Then calculate the area of
these simple geometrical shapes separately.

Area of the square JKLM = 7² cm²

=
49 cm²

Area of the semicircle LNM = (frac{1}{2}) π ∙ ((frac{7}{2})^{2}) cm² , [Since,
diameter LM = 7 cm]

=
(frac{1}{2}) ∙ (frac{22}{7}) ∙ (frac{49}{4}) cm²

=
(frac{77}{4}) cm²

=
19.25 cm²

Step III: Finally, add these areas up to get
the total area of the combined figure.

Therefore, the required area = 49 cm² + 19.25 cm²

=
68.25 cm².

2. In the adjoining figure, PQRS is a square of side 14 cm
and O is the centre of the circle touching all sides of the square.

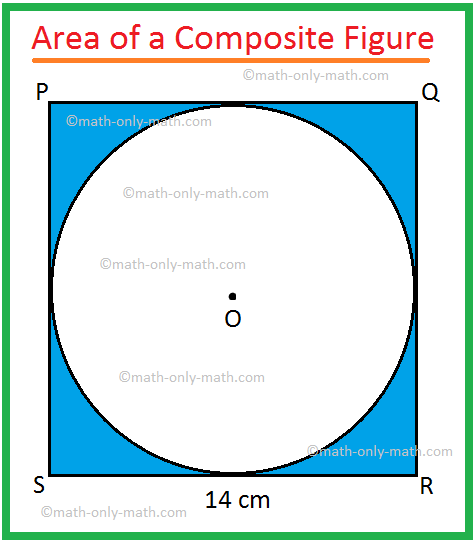
Find the area of the shaded region.

Solution:

Step I: First we divide the combined figure into its simple geometrical shapes.

The given combined shape is combination of a square and a circle.

Step II: Then calculate the area of these simple geometrical shapes separately.

Area of the square PQRS = 14² cm²

= 196 cm²

Area of the circle with centre O = π ∙ 7² cm², [Since, diameter SR = 14 cm]

= (frac{22}{7}) ∙ 49 cm²

= 22 × 7 cm²

= 154 cm²

Step III: Finally, to find the required area of the combined figure we need to subtract the area of the circle from the area of the square.

Therefore, the required area = 196 cm² – 154 cm²

= 42 cm²

3. In the adjoining figure alongside, there are four equal quadrants of circles each of radius 3.5 cm, their centres being P, Q, R and S.

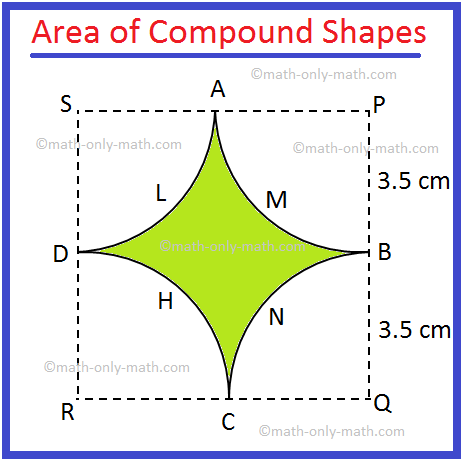
Find the area of the shaded region.

Solution:

Step I: First we divide the combined figure into its simple geometrical shapes.

The given combined shape is combination of a square and four quadrants.

Step II:Then calculate the area of these simple geometrical shapes separately.

Area of the square PQRS = 7² cm², [Since, side of the square = 7 cm]

= 49 cm²

Area of the quadrant APB = (frac{1}{4}) π ∙ r² cm²

= (frac{1}{4}) ∙ (frac{22}{7}) ∙ ((frac{7}{2})^{2}) cm², [Since, side of the square = 7 cm and radius of the quadrant = (frac{7}{2}) cm]

= (frac{77}{8}) cm²

There are four quadrants and they have the same area.

So, total area of the four quadrants = 4 × (frac{77}{8}) cm²

= (frac{77}{2}) cm²

Step III: Finally, to find the required area of the combined figure we need to subtract the area of the four quadrants from the area of the square.

Therefore, the required area = 49 cm² – (frac{77}{2}) cm²

= (frac{21}{2}) cm²

= 10.5 cm²

10th Grade Math

From Areas of Combined Figures to HOME PAGE

Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.

Источник

Т. Г. Кокорева, преподаватель
дисциплины Математика,

ГБПОУ «Челябинский
энергетический колледж имени С.М. Кирова»

УГПС 08.00.00, Специальность
08.02.01 Строительство и эксплуатация зданий и сооружений

ОУДП.01 МАТЕМАТИКА, Раздел 3.
Геометрия 62 часа,

Тема 9. Геометрические тела, площади их
поверхностей и объемы 32 часа

2022

Методическая
разработка открытого учебного занятия

Тема:
«Площади поверхностей комбинированных геометрических тел»

Данная
методическая разработка открытого учебного занятия по теме «Площади
поверхностей комбинированных геометрических тел» в курсе дисциплины ОУДП.01.
Математика предназначена для преподавателей и является примером практического
применения элементов современных педагогических технологий: технология
проблемного обучения (создание преподавателем проблемных ситуаций для
самостоятельной деятельности студентов по их разрешению). В поиске и решении
сложных вопросов, студенты актуализируют знания по текущей теме, проводят
анализ, вырабатывают умения видеть за отдельными фактами явление и закон.
Критическое мышление, кейс технологии, использование ИКТ. В ходе учебного занятия
данные цели и задачи были достигнуты. Формы и методы контроля знаний и умений
обучающихся соответствует целям и задачам занятия. Время учебного занятия
использовано рационально. Присутствует чередование и смена видов деятельности.
В разработке представлено полное методическое обеспечение учебного занятия по
указанной теме. В разработке представлено полное методическое обеспечение
учебного занятия по указанной теме.

1.ВВЕДЕНИЕ

В соответствии с
рабочей программой рабочей дисциплины «Математика» тема «Площади поверхностей
комбинированных геометрических тел» обучающимися 1-го курса специальности 08.02.01
Строительство и эксплуатация зданий и сооружений изучается
согласно КТП во 2-ом семестре. Тема раздела 3. ГЕОМЕТРИЯ. Занятие
№ 106. «Площади поверхностей комбинированных геометрических тел»

Тип занятия: урок применения
знаний и умений

Вид занятия: интегрированный
урок

Методическая цель
урока: организация урока
в соответствии с требованиями ФГОС

Дидактическая цель
занятия:
Организовать деятельность обучающихся по обобщению и систематизации знаний и
способов деятельности,

Задачи занятия: систематизировать
знания и умения по теме: формулы площадей поверхностей геометрических фигур.

Элементы
содержания:
основные формулы для вычисления площадей фигур и объемов тел, используемых в
строительстве;

Цель занятия: отработать
умения и навыки выполнения математических действий при имитации конкретной
производственной ситуации.

Требования к
уровню подготовки обучающихся: Уметь производить расчет площадей
отделываемых поверхностей, объемов работ и расхода материалов, уверенно
работать с калькулятором, переводить единицы измерения.

Организация
(формы) деятельности на уроке: групповая, фронтальная,
индивидуальная.

Технологии обучения: элементы
технологии проблемного обучения, элементы модульной технологии

Обще дидактические
методы обучения:
Информационно-рецептивный, Эвристический, Проблемный, решение ситуационных
профессиональных задач

Оборудование: мультимедиа-проектор,
компьютер, смартфоны

Обучающие средства: презентация (в
Microsoft Power Point), раздаточный материал (карточки, опорный конспект
теоретического и практического материала, индивидуальный лист письменного
ответа).

ХОД
УЧЕБНОГО ЗАНЯТИЯ:

1. Организационный
этап – 2 мин.

2. Постановка целей и
задач урока. Мотивация учебной деятельности обучающихся – 5 мин.

3. Этап
подготовки обучающихся к активному усвоению нового материала – 20 мин.

4. Этап
Обобщения и систематизации знаний

4А. Этап
подготовки обучающихся к обобщенной деятельности -10 мин

4Б. Воспроизведение на новом уровне -13
мин

5.
Применение
знаний и умений в новой ситуации- 5мин

6.
Этап
закрепления вторичных знаний – 10 мин

7. Контроль усвоения,
обсуждение допущенных ошибок и их коррекция – 15 мин.

8. Подведение итогов, рефлексия – 5 мин.

8А. Анализ и содержание итогов работы, формирование выводов по
изученному материалу -2мин

8Б.
Рефлексия-3мин

Технологическая карта учебного занятия

Автор-разработчик	Кокорева Т. Г.
Специальность	08.02.01 Строительство и эксплуатация зданий и сооружений
Учебный цикл	Общеобразовательные дисциплины
УД/МДК	ОУДП.01 Математика
Междисциплинарные связи	МДК 06.01 Производство работ по профессии 13450 Маляр, ПМ.05. Освоение профессий рабочего 19727 Штукатур
Цели учебного занятия	Обучающая	Развивающая	Воспитательная
– систематизировать знания обучающихся по теме «Площади поверхностей комбинированных геометрических тел»; -приобщить обучающихся к систематизации и представлению терминологических единиц для продуктивного усвоения, решения прикладных задач; – закрепить навыки, умения грамотного использования новой терминологии.	– способствовать развитию умения сравнивать, обобщать, анализировать, использовать графический материал; – способствовать развитию логического мышления. – способствовать развитию умения работать в команде.	-содействовать в ходе занятия формированию основных принципов экономического поведения; – воспитание культуры общения; – воспитание потребности в практическом использовании математической терминологии; – стремиться к воспитанию чувства взаимопомощи
Формируемые компетенции	Общие компетенции
ОК 01	Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам
ОК 02	Осуществлять поиск, анализ и интерпретацию информации, необходимой для выполнения задач профессиональной деятельности
ОК 04	Работать в коллективе и команде, эффективно взаимодействовать с коллегами, руководством, клиентами
ОК 05	Осуществлять устную и письменную коммуникацию на государственном языке Российской Федерации с учетом особенностей социального и культурного контекста
ОК 09	Использовать информационные технологии в профессиональной деятельности
	Профессиональные компетенции
ПК 2.3.	Проводить оперативный учет объемов выполняемых работ и расхода материальных ресурсов.
		Личностные результаты
	ЛР 7*	Навыки сотрудничества со сверстниками, детьми младшего возраста, взрослыми в образовательной, общественно полезной, учебно- исследовательской, проектной и других видах деятельности
	ЛР 13*	Осознанный выбор будущей профессии и возможностей реализации собственных жизненных планов; отношение к профессиональной деятельности как возможности участия в решении личных, общественных, государственных, общенациональных проблем.
Наименование и № раздела	Раздел 5. ГЕОМЕТРИЯ	кол-во часов
___62___часа
Наименование и № темы	Тема 5. Геометрические тела, площади их поверхностей и объемы Занятие № 65. «Площади поверхностей комбинированных геометрических тел»	___2___ часа
Тип учебного занятия	Учебное занятие по обобщению и систематизации знаний, умений и способов деятельности.
Вид занятия	Комбинированное
Место проведения учебного занятия	Каб. №422
Форма организации учебного занятия	Групповая, фронтальная, индивидуальная
Внутрипредметные связи	«Тело и поверхность. Многогранники. Вершины, ребра, грани многогранника.», «Понятия площади поверхности. Площадь поверхности многогранников», «Периметр и площадь плоских фигур»
Ресурсы учебного занятия	Материально-технические	Основная литература	Дополнительная литература	Электронно-информационные
– посадочные места по количеству обучающихся; -рабочее место преподавателя; – экранно-звуковые пособия; -информационно-коммуникативные средства/ раздаточный материал.	Геометрия, 10-11: учеб, для общеобразовательных учреждений: базовый и профильный уровни/ [Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.] М.: Просвещение, 2014.	Богомолов Н.В. Практические занятия по математике [Текст]: Учебное пособие для СПО. Доп. Министерством образование РФ/ Н.В. Богомолов. – 7-е изд., стереотип. – Москва: Высшая школа. 2008. – 495 с. Богомолов Н.В. Сборник задач по математике [Текст]: Учебное пособие для СПО. Доп. Министерством образования РФ/ Н.В. Богомолов. – М.: Дрофа, 2008. – 430с.	http://fcior.edu.ru http://school–collection.edu/ru http://widows.edu/ru https://college.ru/matematika/ Приложения: Mentimeter, цифровой конструктор Wordwall, онлайн сервис Study Stack
Формы и методы контроля, оценки результата изучения темы учебного занятия	Текущий контроль – умения высказываться по данной сфере изучения в монологической и диалогической форме, контроль практических умений решения задач на установление соответствий, нахождение стационарных точек, определение интервалов монотонности, точек экстремума.
Задание для внеаудиторной самостоятельной работы	–

Этапы и хронология учебного занятия

Этапы

Содержание

Методические
указания

Признаки
решения дидактических задач / Показатели реального результата решения задачи

Деятельность
преподавателя

Деятельность
обучающегося

1.Организационный

1.Приветствие обучающихся, сообщение
темы занятия

Делятся на подгруппы (до начала занятия)

Приветствие преподавателя, сообщение об
отсутствующих на уроке

Создание благоприятного
психологического климата для работы

Активация знаний о новой
теме / Внимание обучающихся сфокусировано на изучение материала

2.Постановка цели и задач
урока. Мотивация учебной деятельности учащихся

Постановка целей и задач занятия
(организация беседы, помогающей обучающимся сформулировать цели занятия).

– Докажите, что вы не можете начать
завтра ремонт квартиры.

Выявление места и причины затруднения

-Как вы думаете, что необходимо для ремонт
квартиры?

– Какие отделочные материалы нужны?

– Где эти материалы можно взять?

– Что нужно знать и уметь?

(цену и количество материала, уметь
рассчитать, сколько денег нужно заплатить).

– Ваши предложения, что делать с
материалом после покупки? (нужно привести).

Высказывают свои предположения.

(Не могут осуществить поставленную
задачу, т. к. нет материалов, не знают сколько нужно материалов и денег на их
покупку)

обучающиеся самостоятельно
выводят цель и задачи, пытаясь ответить на заданные преподавателем вопросы

Формирование мотивации
деятельности, форма организации деятельности – фронтальная

Сформулированы цели и задачи
урока/

Полная готовность обучающихся к
учебно-познавательной деятельности, готовность оборудования, быстрое
включение обучающихся в работу

3. Этап подготовки обучающихся к
активному усвоению нового материала (Актуализация знаний. Проверка ранее изученного материала. Рассмотрение
различных производственных задач, приводящие к необходимости применения
математического аппарата)

Повторение материала предыдущих занятий:

1. Основные формулы плоских фигур

2. Метрическая система мер.

3. Линейные размеры комнаты.

1)
Для
отделки комнат требуется заказать 20 одинаковых зеркал в одной из трех
фирм. Площадь каждого зеркала 0,35м². В таблице приведены цены на
зеркало, а также на резку зеркал и шлифовку края. Сколько рублей будет стоить
самый дешевый заказ?

Фирма	Цена зеркала (руб. за 1м²)	Резка и шлифовка (руб. за одно стекло)
А	750	80
Б	770	70
В	800	60

2) Пол в комнате, имеет форму
прямоугольника со сторонами 5,5 м и 6 м, требуется покрыть паркетом из
прямоугольных дощечек со сторонами 5 см и 30 см. Сколько потребуется таких
дощечек?

3) 1 Рассчитать количество штукатурной
смеси необходимое для оштукатуривания комнаты жилого дома, размеры которой
приведены на рисунке: размер оконного проема 1500х1200мм.

Норма расхода штукатурной смеси – 10 кг
на 1м2, при толщине слоя -10мм.

2 Рассчитать количество мешков
штукатурной смеси необходимое для работы (1 мешок – 30 кг).

1. Решение заданий (повторение
арифметических действий, действий с дробями)

2. Обсуждение результатов решения

3. Оценивание ответов

Применяется игровой прием – прием
решения прикладных задач, закрепление материала, устная рефлексия, форма организации деятельности – индивидуальная,
фронтальная

Проверено знание формул и их применение
в ходе решения задач/ Готовность
учащихся к активной учебно-познавательной деятельности на основе опорных
знаний.

4.Этап подготовки обучающихся к
обобщенной деятельности

1.Этап
подготовки к решению задачи. Формулировка проблемы.

На изучение и решение кейса, отводится
около 30 минут времени занятия.

Определение проблемы из вопросов:

Задачи для выполнения работы:

1. Внимательно изучить,
проанализировать информацию кейса.

2. На основании анализа работы
сделать выбор покупки продукции для отделки квартиры в определенной фирме, а также
найма рабочих для проведения отделочных работ.

3. Представленные результаты
должны обеспечить:

– максимальное удовлетворение
хозяина квартиры в стоимости отделочного материала.

– экономичность, но
качественность проведения отделочных работ.

Для решения поставленной задачи
подготовлен кейс, в котором имеются характеристики квартиры, условия
проведения ремонта, прайс-листы фирм. Обучающиеся должны произвести
соответствующие практические расчеты и обоснованно объяснить выбор той или
иной фирмы.

форма организации
деятельности – групповая

Информация получена и
используется на практике / Активные действия обучающихся с объектом изучения,
максимальное использование самостоятельности в добывании знаний и овладении
способами деятельности

5. Этап

Применение знаний и умений в
новой ситуации

Для решения поставленной задачи
необходимо рассмотреть прайс-листы трех фирм, ознакомившись с которыми
необходимо выбрать самый оптимальный вариант по закупке строительного
материала и найму рабочих.

Каждая бригада выбирает комнату для
ремонта (выдается карточка-задание). План работы группы:

1. Внимательно изучить материалы кейса

2. Обсудить изученную информацию

3. Обменяться мнениями и составить план
работы над задачей (ситуацией)

4. Проанализировать материал

5. Определить сущность ситуации

6. Зафиксировать основные и
второстепенные проблемы

7. Выработать решение задачи.

требуется найти:

а. стоимость всех материалов;

б. стоимость проводимых работ.

Обучающиеся изучают алгоритм, выявляют
проблему, выбирают оптимальное решение, пользуются раздаточным материалом

форма организации
деятельности –групповая

Информация получена,
принята, осмыслена, сформированы задачи для решения проблемы / Самостоятельное
выполнение заданий, требующих применения знаний из предыдущих тем

6. Этап закрепления вторичных
знаний

произвести отделочные работы в 3-х
комнатной квартире.

Для отделки комнаты необходимо провести
следующие работы:

1. Выровнять стены гипсовой
штукатуркой. Средний расход штукатурки на 1 квадратный метр поверхности при
толщине в 0,1 см составляет 0,9 кг.

2. Покрасить пол масляной
краской 2 раза. В первый раз на каждый квадратный метр пойдет 125 г краски, а
во второй – 75 г.

3. Сделать потолок в каждой
комнате. Для выполнения работы используются плитки квадратной формы со
стороной 50 см, по периметру бордюр.

4. Отделочные материалы выбрать
в одной из трех предлагаемых фирм, исходя из наиболее экономичного варианта стоимости
материала.

Для проведения отделочных работ выбрать
наиболее экономически выгодную бригаду в тех же фирмах.

Посчитать сколько будет стоить самый
выгодный вариант.

Размеры квартиры:

1 комната: 4×5×2,8, имеется
окно, длина которого 2 м и высота 1,5 м, расположенное в стене с меньшими
размерами. Напротив окна находится дверь высотой 2 м и шириной 1 м.

2 комната: 3×3,5×2,8,
имеется окно, длина которого 1,5 м и высота 1,5 м, расположенное в стене с
меньшими размерами. Напротив окна находится дверь высотой 2 м и шириной 1 м.

3 комната: 3,5×4×2,8,
имеется окно, длина которого 2 м и высота 1,5 м, расположенное в стене с
меньшими размерами. Напротив окна находится дверь высотой 2 м и шириной 1 м.

Обучающиеся
решают задачи в группах, определяют свой выбор, ход решения по алгоритму.

форма организации
деятельности –индивидуальная, групповая

Поиск решения проблемы
(задачи), высказывания

Полученная информация
используется на практике/ Активная и продуктивная деятельность учащихся выполнять
подготовительные работы при производстве малярных работ, наносить вручную и
механизированным способом раствор на рабочую поверхность, проводить ремонт
оштукатуренной поверхности и материала в целое по теме занятия,
систематизация, выявлению междисциплинарных связей

7. Этап Контроля

3. Этап проверки
знаний для усвоения материала, практических умений и общих компетенций

Отчёт
о выполнении заданий

	S м² 1 ком	S м² 2 ком	S м2 3 ком	S м² общая	Расход материа-лов	Стоимость материа-лов	Стои-мость работ
Штукатуры
Маляры
Отделка потолков
Итого

Обучающиеся
представляют решение задач от каждой группы, объясняют свой выбор, ход
решения.

форма организации
деятельности –индивидуальная (индивидуализированная)

Оценка правильности
представленного решения задачи / Получение достоверной информации о
достижении всеми учащимися планируемых результатов обучения

Рефлексивно-оценочный
этап

8а. Анализ
и содержание итогов работы, формирование выводов по изученному материалу

Подводя итоги занятия,
преподаватель задает обучающимся следующие вопросы:

1.
Обоснование выбора фирмы для покупки отделочного материала.

2.
Обоснование выбора фирмы для проведения отделочных работ.

3.
Стоимость отделочных работ квартиры.

Выставление оценок в
соответствии с листом критериев оценки в группе.

Обучающиеся участвуют в
общей дискуссии, формулируют конечный результат своей работы на занятии,
определяют, чье решение было оптимальным, отвечают на вопросы, прослушивают
варианты наиболее оптимального решения задач

Формирование определять методы и способы
выполнения практических задач, оценивать их эффективность и качество.

форма организации
деятельности –фронтальная, индивидуальная

Выявление сложных моментов в работе,
указание на слабые места и сильные стороны отвечающих / Получение
учащимися информации о реальных результатах учения.

8б. Рефлексия

Преподаватель предлагает
оценить результаты своей деятельности, ответив на вопросы:

– Как вы оцениваете свою
работу на занятии?

– Чему научились на занятии?

– Какие рассмотренные задачи
оказались наиболее сложными? Почему?

– Можете ли вы теперь дать
ответ на вопрос о необходимости математических знаний?

Обучающиеся выявляют
непонятные моменты и сложности при изучении материала, при выполнении
задания

Мобилизация обучающихся на рефлексию
своей деятельности (мотивации, способов деятельности, общения)

Открытость учащихся в осмыслении своих
действий и в их самооценке.

Прайс – лист
Фирма	Наименование работ	Цена
	Гипсовая штукатурка	284 руб. (25 кг)
Потолочная плитка	21 руб. (1 шт.)
Потолочный бордюр	17 руб. (1 м²)
Краска для пола	255 руб. (4 кг) 71 руб. (1 кг)
	Гипсовая штукатурка	270 руб. (25 кг)
Потолочная плитка	24 руб. (1 шт.)
Потолочный бордюр	13 руб. (1 м²)
Краска для пола	240 руб. (4 кг) 74 руб. (1 кг)
	Гипсовая штукатурка	280 руб. (25 кг)
Потолочная плитка	22 руб. (1 шт.)
Потолочный бордюр	15 руб. (1 м²)
Краска для пола	250 руб. (4 кг) 70 руб. (1 кг)

Прейскурант цен на стоимость услуг
Фирма	Наименование работ	Цена (1 м²)
	Шпатлевка и шлифовка стен	110 руб.
Покраска пола	85 руб.
Ремонт потолка	100 руб.
	Шпатлевка и шлифовка стен	140 руб.
Покраска пола	60 руб.
Ремонт потолка	70 руб.
	Шпатлевка и шлифовка стен	120 руб.
Покраска пола	75 руб.
Ремонт потолка	80 руб.

Скачано с www.znanio.ru

Т. Г. Кокорева, преподаватель дисциплины

Методическая разработка открытого учебного занятия

ВВЕДЕНИЕ В соответствии с рабочей программой рабочей дисциплины «Математика» тема «Площади поверхностей комбинированных геометрических тел» обучающимися 1-го курса специальности 08

Применение знаний и умений в новой ситуации- 5мин 2

Технологическая карта учебного занятия

ЛР 13* Осознанный выбор будущей профессии и возможностей реализации собственных жизненных планов; отношение к профессиональной деятельности как возможности участия в решении личных, общественных, государственных, общенациональных…

Этапы и хронология учебного занятия

Проверка ранее изученного материала

На основании анализа работы сделать выбор покупки продукции для отделки квартиры в определенной фирме, а также найма рабочих для проведения отделочных работ

Покрасить пол масляной краской 2 раза

Рефлексивно-оценочный этап 8а

Прайс – лист Фирма

Источник

Задачи на комбинированные поверхности

Как подготовиться к экзамену?

Описание презентации по отдельным слайдам:

Т. Г. Кокорева, преподаватель дисциплины

Методическая разработка открытого учебного занятия

Применение знаний и умений в новой ситуации- 5мин 2

Технологическая карта учебного занятия

Этапы и хронология учебного занятия

Проверка ранее изученного материала

На основании анализа работы сделать выбор покупки продукции для отделки квартиры в определенной фирме, а также найма рабочих для проведения отделочных работ

Покрасить пол масляной краской 2 раза

Рефлексивно-оценочный этап 8а

Прайс – лист Фирма

Вам также может понравиться

Как найти настоящую свою половинку

Как составить бизнес план в excel

Как найти радиус окружности с помощью треугольника

Добавить комментарий Отменить ответ