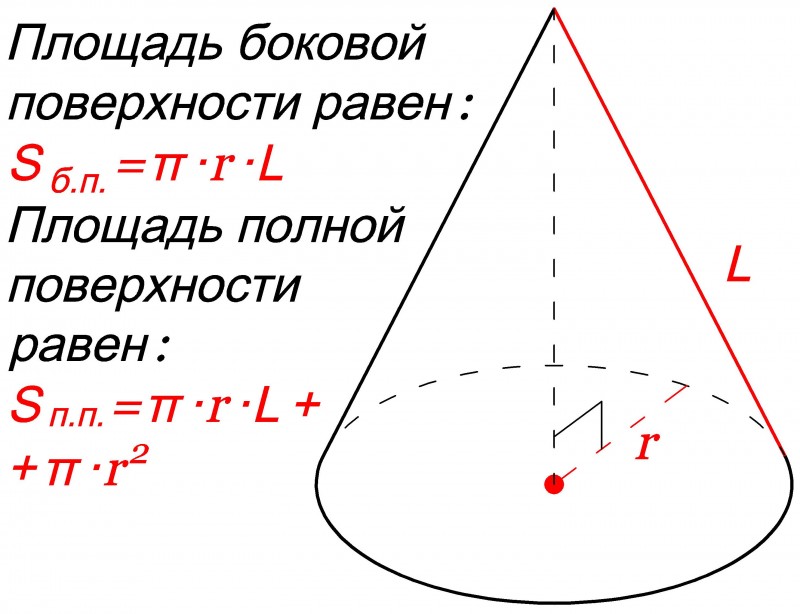
Как рассчитать площадь поверхности конуса
На данной странице калькулятор поможет рассчитать площадь поверхности конуса онлайн. Для расчета задайте высоту, радиус или образующую.
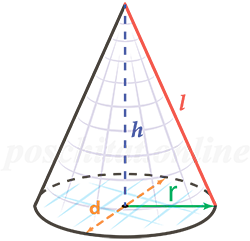
Конус – геометрическое тело, образованное вращением прямоугольного треугольника около одного из его катетов.
Образующая конуса – это отрезок, соединяющий вершину и границу основания.
Боковая поверхность через радиус и образующую
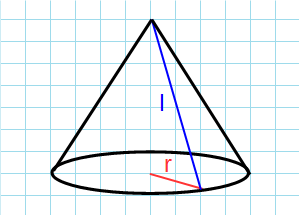
Формула боковой поверхности конуса через радиус и образующую:
π – константа равная (3.14); l – образующая конуса; r – радиус основания конуса.
Боковая поверхность через радиус и высоту
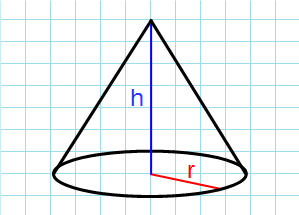
Формула боковой поверхности конуса через радиус и высоту:
π – константа равная (3.14); h – высота конуса; r – радиус основания конуса.
Полная площадь через радиус и образующую

Формула площади полной поверхности конуса через радиус и образующую:
π – константа равная (3.14); l – образующая конуса; r – радиус основания конуса.
Полная площадь через радиус и высоту

Формула полной площади поверхности конуса через радиус и высоту:
π – константа равная (3.14); h – высота конуса; r – радиус основания конуса.
Площадь поверхности конуса
- Главная
- /
- Математика
- /
- Геометрия
- /
- Площадь поверхности конуса
Для того чтобы посчитать площадь поверхности конуса, просто воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
Площадь боковой поверхности конуса
=
=
Sб.пов =
0
Округление числа π: Округление ответа:
Площадь полной поверхности конуса
=
=
Sп.пов =
0
Округление числа π: Округление ответа:
Просто введите данные, и получите ответ.
Теория
Площадь боковой поверхности конуса через образующую
Чему равна площадь боковой поверхности конуса Sб.пов, если образующая l, а радиус основания r:
Формула
Sб.пов = π ⋅ r ⋅ l
через диаметр:
Sб.пов = π ⋅ l ⋅ d⁄2
Пример
Для примера посчитаем чему равна площадь боковой поверхности конуса, образующая которого l = 6 см, а радиус основания r = 3 см:
Sб.пов ≈ 3.14 ⋅ 6 ⋅ 3 ≈ 56.52 см²
Площадь боковой поверхности конуса через высоту
Чему равна площадь боковой поверхности конуса Sб.пов, если высота h, а радиус основания r:
Формула
Sб.пов = π ⋅ r ⋅ √r² + h²
через диаметр:
Sб.пов = π ⋅ d⁄2 ⋅ √(d/2)² + h²
Пример
Для примера посчитаем чему равна площадь боковой поверхности конуса, высота у которого h = 5 см, а радиус основания r = 2 см:
Sб.пов ≈ 3.14 ⋅ 2 ⋅ √2² + 5² ≈ 6.28 ⋅ √29 ≈ 33.82 см²
Площадь полной поверхности конуса через образующую
Чему равна площадь полной поверхности конуса Sп.пов, если образующая l, а радиус основания r:
Формула
Sп.пов = π ⋅ r ⋅ (r + l)
через диаметр:
Sп.пов = π ⋅ d⁄2 ⋅ (d⁄2 + l)
Пример
Для примера посчитаем чему равна площадь полной поверхности конуса, образующая которого l = 6 см, а радиус основания r = 3 см:
Sп.пов ≈ 3.14 ⋅ 3 ⋅ (3 + 6) ≈ 84.78 см²
Площадь полной поверхности конуса через высоту
Чему равна площадь полной поверхности конуса Sп.пов, если высота h, а радиус основания r:
Формула
Sп.пов = π ⋅ r ⋅ (r + √r² + h²)
через диаметр:
Sп.пов = π ⋅ d⁄2 ⋅ (d⁄2 + √(d/2)² + h²)
Пример
Для примера посчитаем чему равна площадь полной поверхности конуса, высота у которого h = 5 см, а радиус основания r = 2 см:
Sп.пов ≈ 3.14 ⋅ 2 ⋅ (2 + √2² + 5²) ≈ 6.28 ⋅ (2 + √29) ≈ 46.38 см²
См. также
При помощи нашего калькулятора вы легко сможете узнать площадь конуса.
Для того что бы вычислить площадь конуса необходимо знать его радиус или диаметр. Если нам известна одна из указанных величин, для нас не составит труда вычислить площадь.
Площадь конуса рассчитывается по следующим формулам:
- Если нам известен радиус:
Формула для расчета полной поверхности конуса через радиус:
S=πr(r+l)Формула для расчета боковой поверхности конуса через радиус:
S=πrl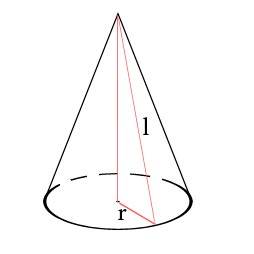
- Если нам известен диаметр:
Формула для расчета полной поверхности конуса через диаметр:
S=πD/2(D/2+l)Формула для расчета боковой поверхности конуса через диаметр:
S=πDl/2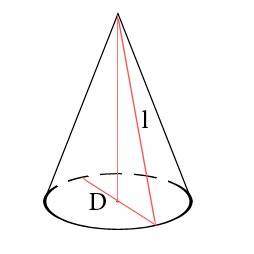
Где S – площадь, r – радиус, D – диаметр, l – образующая, π – число Пи которое всегда примерно равно 3,14.
Площадь конуса вычисляется путем суммирования значений S лежащего в основании круга и S боковой поверхности фигуры. Исходными данными для ее вычисления является радиус R и образующая l, площадь конуса вычисляется по формуле S = π х R х (R + l).
Образующая боковой поверхности l – отрезок, соединяющий вершину конуса и любую точку базисной окружности основания данной геометрической фигуры. Калькулятор вычисляет площадь конуса после внесения исходных данных в соответствующие поля формы на странице и нажатия кнопки «Вычислить».
Конус является одной из элементарных объемных геометрических фигур, из которых состоят сложные детали различных инженерных сооружений и конструкций. Конструкторам и проектировщикам в их работе довольно часто требуется вычислять S конуса.
Потребность в расчете площади конуса может быть необходима для последующего выяснения значений важных показателей эксплуатационных нагрузочных и прочностных характеристик, приходящихся на единицу площади фигуры. С учетом S конуса выбирается соответствующий исходный материал, из которого будет изготовлена проектируемая деталь.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

|
Объем конуса через радиус (r) основания |
|
|
|
Радиус (r):
Высота (h): Объем конуса (Vк): |
|
Объем конуса через площадь основания (Sосн) |
|
|
|
Площадь основания (Sосн):
Высота (h): Объем конуса (Vк): |
|
Площадь боковой поверхности и полная площадь поверхности |
|
|
|
Радиус (r):
Длина образующей (L): Площадь боковой поверхности (Sб.п.): Площадь полной поверхности (Sп.п.): |
|
Конус — это геометрическое тело, которое образовано совокупностью всех лучей,
Круглый конус – это тело, состоящее из круга (основание конуса), точки, |
|
|
|