Как найти площадь треугольника – все способы от самых простых до самых сложных
Зависит от того, какой треугольник.
Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.
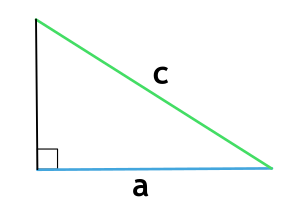
Если треугольник прямоугольный
То есть один из его углов равен 90 градусам.
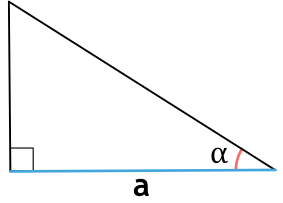
Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.
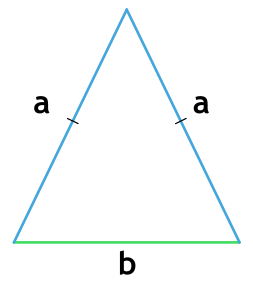
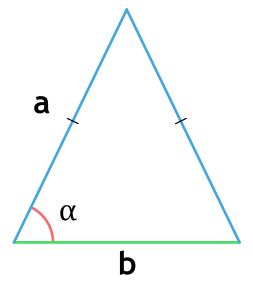
Если он равнобедренный
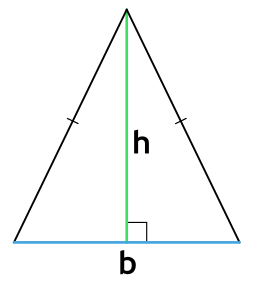
То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.
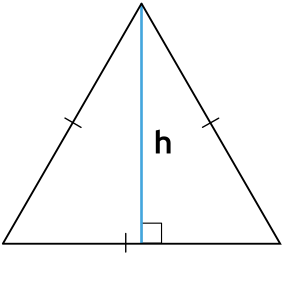
Если он равносторонний
То есть все три стороны равны. Ваши действия такие:
- Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
- Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
- Поделите все на 4.
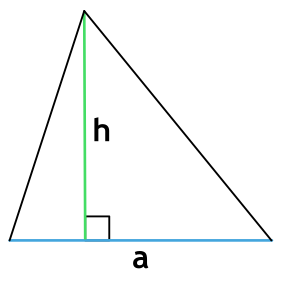
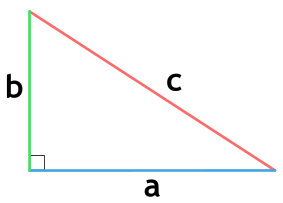
Если известна сторона и высота
Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.
Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.
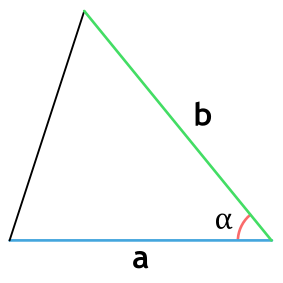
Если известны две стороны и градус угла между ними
Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:
Если известны длины трех сторон
- Найдите периметр. Для этого сложите все три стороны.
- Найдите полупериметр – разделите периметр на два. Запомните значение.
- Отнимите от полупериметра длину первой стороны. Запомните.
- Отнимите от полупериметра длину второй стороны. Тоже запомните.
- Отнимите от полупериметра длину третьей стороны. И ее запомните.
- Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
- Найдите квадратный корень.
Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.
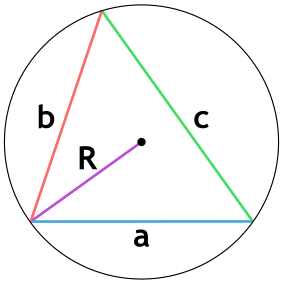
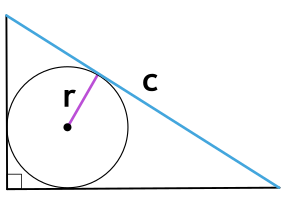
Если известны три стороны и радиус описанной окружности
Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.
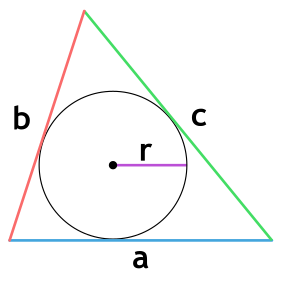
Если известны три стороны и радиус вписанной окружности
Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.
Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.
Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.
Как найти площадь косоугольного треугольника
РЕШЕНИЕ КОСОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ
При решении прямоугольных треугольников мы использовали только определения основных тригонометрических функций. Для решения же косоугольных треугольников нам потребуется знание зависимостей между сторонами и тригонометрическими функциями углов косоугольных треугольников, известные как теоремы синусов, косинусов и тангенсов. К выводу этих теорем мы и переходим.
В дальнейшем мы будем пользоваться следующими обозначениями: a, b и с — стороны треугольника; А, В и С — противолежащие им углы; S — площадь; 2р — периметр; R — радиус описанного круга; r — радиус вписанного круга; hа, lа и mа — высота, биссектриса и медиана, соответствующие стороне а.
1. Теорема синусов
Теорема. Во всяком треугольнике стороны пропорциональны синусам противолежащих углов:
Доказательство. Опишем круг около данного треугольника ABC . Пусть R — радиус этого круга. Возьмём одну из вершин треугольника, например А; через одну из других вершин, например через В, проведём диаметр ВА’ описанного круга. Вспомогательный треугольник А’ВС прямоугольный, так как вписанный угол А’СВ опирается на диаметр. Из вспомогательного треугольника найдём:
Если угол А острый, то А = А’, так как вписанные углы A и A’ опираются на одну и ту же дугу.
Если угол А тупой, то угол А’ острый, измеряющийся половиной дуги ВАС:
Итак, или A = А’, или A’ = — A, в обоих случаях sin A’ = sin A, а потому
Если угол A прямой, то а = 2R, sin A = 1 и равенство (1) также справедливо.
Аналогичные равенства найдём и для прочих углов В и С. Итак,
а = 2R sin A; b = 2R sin В; с = 2R sin С, откуда
= 2R
Следствие. Отношение стороны треугольника к синусу противолежащего угла равно диаметру круга, описанного около треугольника.
2. Теорема косинусов
Теорема. Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними:
Доказательство. Докажем первое равенство.
Случай 1. Угол A острый.
Пусть ВН — высота, опущенная из вершины В ; из геометрии известно (см. А.Киселев Геометрия . Планиметрия. Книга3, глава3,теорема 208) , что
а 2 = b 2 + с 2 -2b · АН. (1)
Из прямоугольного треугольника АВН найдём
АН = с cos А; подставив в формулу (1), получим доказываемое равенство.
Случай 2. Угол A тупой.
В этом случае а 2 = b 2 + с 2 +2b · АН. (2)
(см. А.Киселев Геометрия . Планиметрия. Книга3, глава3,теорема 209)
Из треугольника АВН найдём:
АН = с cos / BAH= с cos ( -A) = — с cos A.
Подставив в формулу (2), получим доказываемое равенство.
Случай 3. Угол А прямой.
В этом случае (по теореме Пифагора): а 2 = b 2 + с 2 = b 2 + с 2 – 2bc cos А (так как cos А = 0).
Итак, во всех случаях
3. Формулы для вычисления площади треугольника
1. Из геометрии известна формула Г е р о н а: S = / р (р – а)(р – b) (р – с) (где р = (а+ b+c)/2 -полупериметр ), позволяющая вычислять площадь треугольника по его сторонам.
2. Теорема. Площадь треугольника равна половине произведения двух сторон на синус угла между ними:
S = 1 /2 bc sin A.
Доказательство. Из геометрии известно, что площадь треугольника равна половине произведения стороны треугольника на высоту, опущенную на эту сторону из противоположной вершины.
Если угол А острый, то из треугольника АВН найдём ВН = hb = с sin A.
Если угол A тупой, то ВН = hb = с sin ( -A) = с sin A. Если угол A прямой, то sin A = 1 и
hb = АВ = с = с sin A.
Следовательно, во всех случаях hb = с sin A. Подставив в равенство (1), получим доказываемую формулу.
Точно так же получим формулы: S = 1 /2 ab sin C = 1 /2 ac sin B
3. На основании теоремы синусов:
Подставив эти выражения в формулу (1), получим следующую формулу:
Теорема. Разность двух сторон треугольника относится к их сумме, как тангенс полуразности противолежащих углов к тангенсу полусуммы этих углов:
(и две аналогичные формулы для прочих пар сторон а, с и b, с).
Доказательство. В силу теоремы синусов имеем:
Разделив почленно эти равенства, получим доказываемую формулу.
5.Решение треугольника по двум его углам и стороне
Задача. Даны два угла треугольника и сторона, прилежащая к ним; вычислить другие стороны и угол.Даны В, С и а; требуется найти b, с и А.
Решение. Условие возможности построения треугольника по этим данным: А + В / а 2 + b 2 — 2ab cos С
Для вычисления А можно также воспользоваться формулой косинусов:
Так как 0 b, т. е, заданный угол А лежит против большей стороны.
Построение показано на чертеже. Из точки С (как из центра), взятой на одной из сторон угла А на расстоянии b от вершины, описана окружность радиуса а; точка В есть точка пересечения этой окружности с другой стороной угла А.
Построение всегда возможно, задача имеет единственное решение.
Острый угол В, противолежащий меньшей стороне, находится по теореме синусов:
откуда
и затем С = 180° — (A + В). Сторона с находится по теореме синусов:
С л у ч а й 2. а 90° задача не имеет решения.
Пусть угол А острый. Из построения на чертеже a) , видно, что окружность радиуса а с центром в точке С пересечёт другую сторону угла А в двух точках при условии а > CD, где D — основание перпендикуляра, опущенного из точки С на другую сторону угла A. Так как CD = b sin A (из треугольника ACD), то условие запишется так: a >bsinA. Для угла В возможны два значения: В = В1 (острый) и В = В2 (тупой). Задача имеет два решения.
Значения угла В вычисляются по теореме синусов:
откуда и B2 = 180° – B1 Значения угла С и стороны с вычисляются так же, как в предыдущем случае.
Из чертежа b) видно, что при CD = b sin А > а окружность не пересечёт другой стороны угла А; задача не имеет решений.
В этом случае и угол В вычислить нельзя.
При CD = b sin А задача имеет единственное решение: треугольник ABC прямоугольный.
Случай 3. а = b. В этом случае треугольник ABC равнобедренный. Такой треугольник можно решить, разбразбив его высотой CD на два прямоугольных треугольника:
В = А; С = 180° — 2А; с = 2AD = 2а cos A.
8.Решение треугольника по трём сторонам
Задача. Даны три стороны треугольника; вычислить его углы.
Пусть даны длины трёх сторон треугольника. Обозначим через а меньшую сторону, через b — среднюю, а через с — большую: а а + b, то треугольник с данными сторонами не существует. Будем считать, что с 2 =b 2 + с 2 – 2bc cos А
b 2 =c 2 + a 2 – 2ca cos B, откуда
и (тал как 0° / р (р – а)(р – b) (р – с) , где р = (а+ b+c)/2
Имеем далее: S = 1 /2 bc sin A. откуда
Угол А острый, так как он лежит против меньшей стороны; следовательно,
и, наконец, С = 180° — (А + В)
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона
Формула Герона для нахождения площади треугольника:
Через основание и высоту
Формула нахождения площади треугольника с помощью половины его основания и высоту:
Через две стороны и угол
Формула нахождения площади треугольника через две стороны и угол между ними:
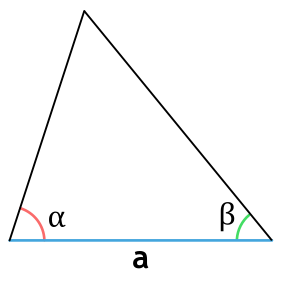
Через сторону и два прилежащих угла
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
Площадь прямоугольного треугольника
Прямоугольный треугольник – треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
Площадь равнобедренного треугольника через стороны
Равнобедренный треугольник – треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
Площадь равнобедренного треугольника через основание и угол
Формула нахождения площади равнобедренного треугольника через основание и угол:
Площадь равностороннего треугольника через стороны
Равносторонний треугольник – треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
Площадь равностороннего треугольника через высоту
Формула нахождения площади равностороннего треугольника через высоту:
Площадь равностороннего треугольника через радиус вписанной окружности
Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
Площадь равностороннего треугольника через радиус описанной окружности
Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
Площадь треугольника через радиус описанной окружности и три стороны
Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
Площадь треугольника через радиус вписанной окружности и три стороны
Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
[spoiler title=”источники:”]
http://oldskola1.narod.ru/trig03.htm
http://mozgan.ru/Geometry/AreaTriangle
[/spoiler]
Презентация на тему: ” Знакомства с площадью параллелограмма, площадью прямоугольного треугольника и площадью косоугольного треугольника.” — Транскрипт:
1
Знакомства с площадью параллелограмма, площадью прямоугольного треугольника и площадью косоугольного треугольника.
2
«Прежде, чем доказывать мы должны научиться догадываться»
3
4
Прямоугольник Параллелограмм Квадрат Ромб Равнобедренный треугольник Восьмиугольник Трапеция Прямоугольный треугольник
5
Вставьте пропущенные слова Равные многоугольники имеют……….. площади. Если многоугольник составлен из нескольких многоугольников, то площадь равна сумме …………. этих многоугольников. равные площадей
6
Вычислите площади фигур
7
Постановка задачи: Требуется выполнить работу по настилке паркетного пола в игровом зале размером 5,75 х 8 м. Паркетные плитки имеют форму прямоугольных треугольников и параллелограммов. Размеры плиток указаны в сантиметрах на рисунке. Нужно учесть, что стоимость плитки в виде треугольника и стоимость плитки в виде параллелограмма равна. Сколько нужно купить плиток при самом экономичном варианте
8
Задачи из учебника: 459 (а); 468(а); 471(а).
9
ТЕСТ Выберите правильный ответ. (Каждая задача оценивается в один балл). 1. Площадь прямоугольного треугольника, катеты которого равны а и в вычисляется по формуле: А. S=ав Б. S=ah В. S=а+в 2. Площадь параллелограмма равна: А. Произведению его основания на высоту. Б. Половине произведения его основания на высоту. В. Произведению его смежных сторон. 3. Площадь параллелограмма равна 125 см,а его основание 25 см, высота А. 4 Б. 5 В Площадь треугольника равна половине произведения его основания на А. Высоту. Б. Основание. В. Произведение его смежных сторон. 5. Площадь треугольника равна 125 см,а его основание 25 см, высота А. 10 Б. 1 В. 0
10
Ключ к проверке теста ААБАА
11
Домашнее задание: Принести модель трапеции В рабочей тетради 35;47;54
ВИДЕО УРОК
Условимся, как это принято, обозначать элементы
косоугольного треугольника с вершинами А, В, С следующими буквами
А,
В, С – внутренние углы треугольника;
a,
b, c – соответствующие
стороны, противоположные углам треугольника;
ha,
hb, hc –
высоты треугольника относительно сторон a, b и с;
ba,
bb, bc –
биссектрисы внутренних углов;
ma, mb,
mc – соответствующие медианы;
– полупериметр треугольника;
S – площадь треугольника;
R – радиус описанной окружности;
r – радиус вписанной окружности;
ra,
rb, rc –
радиусы вневписанных окружностей.
Основные теоремы и формулы о соотношениях между элементами треугольника.
Сума
внутренних углов.
Формулы половинных
углов.
Формула для высот треугольников.
Формулы для вычисления
биссектрис.
Формула для вычисления
медиан.
Формулы для вычисления
радиуса описанной окружности.
Формулы для вычисления
радиуса вписанной окружности.
Основные случаи решения косоугольных треугольников.
Основными случаями решения треугольников называются задачи на вычисление
элементов треугольника по трём его данным независимым основным элементам.
К основным элементам относят стороны и внутренние углы треугольника, причем
углы связаны между собой соотношением
А
+ В + С = π,
поэтому только два из них могут быть независимыми.
Решение косоугольного
треугольника по стороне и двум углам.
В треугольнике АВС даны:
сторона а и углы В и С. Найти угол А и стороны
b и с.
Если даны два угла треугольника, то третий определяем как
А
=180° – (В + С).
Неизвестные стороны b и с определяются по теореме синусов из пропорций:
Откуда получаем:
но
sin А = sin
[180° –
(В + С)] = sin (В + С),
а потому
ПРИМЕР:
Дано:
а = 400,
А = 36°40‘,
В = 79°50‘.
Найти b, с, С.
РЕШЕНИЕ:
1) С = 180° – (А + В),
С = 180° – (36°40‘ + 79°50‘) = 69°30‘.
В последнем случае при определении стороны с можно
было взять и такую пропорцию:
Но в эту пропорцию
введём только что найденную сторону b. Если при отыскании
b была допущена ошибка, то она отразится и на
величине с, несмотря на безошибочные вычисления при определении
последней.
ПРОВЕРКА:
Найдём угол
С через
найденные стороны b и с по
формуле:
Имеем:
Имеем совпадение с полученным ранее результатом.
Решение косоугольного
треугольника по двум сторонам и углу, противолежащему одной из них.
ПРИМЕР:
Пусть в треугольнике
АВС даны: стороны а, b и угол
А.
требуется найти сторону с и углы В и С.
РЕШЕНИЕ:
Угол В определяется
по теореме синусов. Имеем:
Откуда
Угол С находится из
соотношения
С = 180° – (А + В).
Из пропорции
находим с:
Для построения
треугольника по двум его данным сторонам
а и b и
углу А, противолежащему стороне а, можно поступить так: строим угол
А
и на одной из его сторон от точки А откладываем отрезок АС
= b. Затем строим окружность радиуса а с центром в точке С.
Если эта окружность не пересечёт второй стороны угла А,
то задача не имеет решения (случай I), если эта
окружность коснётся второй стороны угла, то задача имеет одно решение (случай II
– искомый
треугольник АСВ1), если эта окружность пересечёт вторую
сторону угла, то задача имеет два решения (случай III, треугольники АСВ2 и АСВ3) и, наконец, если окружность пересечёт
сторону угла лишь в одной точке, то задача имеет одно решение (случай
IV, АСВ4).
На чертеже
рассмотрен случай, когда
угол А – острый. На следующем чертеже
рассмотрен случай, когда этот угол тупой. В этом случае
задача или не имеет решения (I) или имеет только одно решение (II).
Пусть угол
А – острый. Тогда как следует из чертежа
в случае
а < b sin А
задача не имеет решения (I), в случае
а = b sin А
задача имеет одно решение (II), если
b ˃ а ˃
b sin А,
задача имеет два решения (III), наконец,
если а ≥ b,
задача имеет одно решение (IV).
Если угол
А – тупой, то в случае а ≤ b задача не имеет решения (I), а в случае а ˃ b – имеет и при том только одно решение (II).
ПРИМЕР:
Дано:
а = 242,
b = 767,
В = 36°53‘.
Найти с, А, С.
РЕШЕНИЕ:
Так как угол
В – острый и
b ˃ а, то задача имеет решение и, причём, только
одно.
(А – острый угол, так как а < b
и А < В).
2) С = 180° – (А + В),
С ≈180° – (10°55‘ + 36°53‘) = 132°12‘.
ПРОВЕРКА:
Вычислим по следующей формуле угол В.
Имеем совпадение с данным значением угла В.
ПРИМЕР:
Дано:
а = 400,
b = 500,
А = 40°.
Найти с, В, С.
РЕШЕНИЕ:
Так как угол
А – острый и
b ˃ а ˃ b sin А, то задача имеет два решения
Первое решение найдено. Второе решение найдём,
приняв В равным
180° – 53°28‘ = 126°32‘.
Угол С будет другой, а в
связи с этим изменится и сторона с. Обозначим эти новые значения соответственно через
В‘, С‘, с‘.
Имеем:
1) В‘ =
126°32‘.
2) С‘ = 180° – (А + В‘),
С‘ ≈180° – (40° + 126°32‘) = 13°28‘.
Следовательно, имеется два различных треугольника, у
которых
а = 400,
b = 500,
А = 40°,
один из них – остроугольный, другой – тупоугольный.
Построение треугольника при этих данных подтверждает полученные два ответа.
ПРИМЕР:
Дано:
а = 165,
b = 268,
А = 53°08‘.
Найти с, В, С.
РЕШЕНИЕ:
Имеем
b sin А ≈ 268 ∙ 0,8000 ˃ а =
165,
Следовательно, задача не имеет решений.
Формулы для определения угла
треугольника по двум его сторонам и углу между ними.
ТЕОРЕМА:
ДОКАЗАТЕЛЬСТВО:
Рассмотрим сначала
случай, когда угол С – острый.
Проведём из вершины В высоту
ВD = h.
Из прямоугольного
треугольника АВD получаем
соотношение
Из треугольника ВСD находим:
h = a sin C
и далее:
AD = AC – DC,
DC = a cos C.
Равенство
AD = AC – DC
теперь представится в таком виде:
AD = b – a cos C.
Выражение для h из равенства
h = a sin C
и AD из равенства
AD = b – a cos C
подставляем в
Получим:
В случае, когда
С – тупой,
получим:
Но
h = a sin (180° – C) = a sin C,
а
СD = a соs (180° – C) = –a соs C.
На основании
h = a sin C
и
СD = –a соs C
равенство
примет вид:
Аналогично доказывается и равенство
Выражения для
tg В и tg С
представляется в такой форме:
Решение косоугольного
треугольника по двум сторонам и углу между ними.
ПРИМЕР:
В треугольнике АВС дано: стороны а и b и угол С.
Найти сторону с и углы А и В.
РЕШЕНИЕ:
1-й способ. По теореме косинусов имеем:
c2 = a2 + b2
– 2ab cos C.
Откуда получим с.
Угол А находим
по теореме синусов. Имеем:
откуда
Точно так же из
пропорции
получим
Углы в рассмотренном
случае отыскиваем по теореме синусов. Угол, лежащий против большей стороны
треугольника, следует искать последним. Например, если а ˃ b, то угол
В – острый. Определив из
этот острый угол В, находим угол А:
А = 180° – (В + С).
Контролем может служить формула
2-й способ. Выражаем тангенс одного из искомых
углов, например tg A, через данные
a, b и С по
формуле:
Угол В находим из
соотношения:
B = 180° – (A + С).
Сторону с находим,
пользуясь теоремой синусов:
Первым способом
целесообразно пользоваться, если ищется только сторона, а вторым – если только
угол.
Каждый из этих
способов может быть использован для проверки решения другим способом.
ПРИМЕР:
Дано: а = 320, b = 400, С = 110°21‘.
Найти с, А и В.
РЕШЕНИЕ:
Первый способ.
1) По
теореме косинусов имеем:
c2 = a2 + b2
– 2ab cos C.
Откуда получим с:
c2 = 3202 + 4002
– 2 ∙ 320 ∙ 400 cos 110°21‘ =
3202 + 4002 – 2 ∙
320 ∙ 400 cos 69°39‘ ≈
102 400 + 256 000 ∙ 0,3478 ≈ 351 437.
с ≈
592,8.
В ≈ 39°15‘.
ПРОВЕРКА:
110°21‘ + 30°24‘ + 39°15‘ = 180°.
Второй способ.
В ≈ 39°15‘.
2) А =
180° – (В + С),
А ≈ 180° – (39°15‘ + 110°21‘) = 30°24‘.
Формулы для определения углов треугольника по трём его сторонам.
Возьмём треугольник АВС.
Впишем в него круг радиуса r.
Центр О этого круга
находится на пересечении биссектрис внутренних углов треугольника.
Пусть D, Е, F
точки, в которых
стороны треугольника касаются окружности.
Из геометрии известно, что отрезки двух касательных, проведённых из одной
точки к окружности, равны между собой. На этом основании можем заключить о
равенстве следующих отрезков, входящих в состав сторон треугольника:
AD
= AF = k,
BD
= BE = m,
CE
= CF = n.
Если проведём радиусы
OD,
OE, OF
в точки касания, то образуются шесть прямоугольных треугольников.
Из треугольника AOF имеем:
выразим r и k через стороны
треугольника a,
b, c. Из чертежа видно,
что
a
+ b + c = 2k + 2m + 2n.
Если периметр треугольника обозначим через
2p, то получим
2p = 2k + 2m
+ 2n,
откуда
p
= k + m + n.
Так как m
+ n = a, то из равенства
p
= k + m + n
получим, что
k
= p – a.
Из геометрии известно, что r круга, вписанного в треугольник, выражается
через полупериметр p и стороны его так:
На основании равенств
равенство
примет вид:
По аналогии получатся формулы
то есть во всяком треугольнике тангенс половины
одного из его углов равен квадратному корню из дроби, у которой числитель есть
произведение разностей между полупериметром треугольника и каждой из сторон,
образующих угол, а знаменатель – произведение полупериметра на разность между
полупериметром и стороной, противолежащей этому углу.
Так как A,
B, C – углы треугольника, то половины их A/2, B/2, C/2 – всегда углы острые. Поэтому
tg A/2, tg B/2, tg C/2
положительны.
Формулы для определения углов
треугольника по трём его сторонам с помощью теоремы косинусов.
Теорема косинусов
даёт такую зависимость между тремя сторонами треугольника и углом:
a2 = b2 + с2
– 2bс cos А.
Выразив из этого
равенства cos А, получим:
так же можно по аналогии написать выражения для
косинусов остальных углов:
Решение
косоугольного треугольника по трём сторонам.
В
треугольнике АВС
даны стороны а, b, с. Требуется найти углы
А, В и С треугольника.
Углы А, В и С треугольника
можно определить по формулам, выражающим
cos А, cos В, cos C
через стороны треугольника:
Или
же углы А, В и С определяются по
формулам, выражающим
tg
А/2, tg В/2, tg С/2.
через а, b, с:
ПРИМЕР:
Дано: а = 13, b = 18, с = 15.
Найти А, В и
С.
РЕШЕНИЕ:
Первый способ.
ПРОВЕРКА:
А + В + С =
45°16‘ + 79°40‘ + 55°4‘ = 180°.
Второй способ.
Имеем:
2р = 13 + 18 + 15 = 4,
р = 23,
р – а =10,
р – b = 5,
р – с = 8.
ПРОВЕРКА:
(р – а) + (р – b) + (р – с) =
раскроем скобки
р – а + р – b + р
– с =
сгруппируем и приведём подобные члены
3р – (а + b + с) =
Так как (а + b + с) это периметр Р = 2р, то получаем:
3р – 2р = р.
10 + 5 + 8 = 23.
Получились те же
значения углов, что и при решении первым способом.
Задания к уроку 16
- Задание 1
- Задание 2
- Задание 3
ДРУГИЕ УРОКИ
- Урок 1. Градусное измерение угловых величин
- Урок 2. Радианное измерение угловых величин
- Урок 3. Основные тригонометрические функции
- Урок 4. Натуральные тригонометрические таблицы
- Урок 5. Периодичность тригонометрических функций
- Урок 6. Область определения и область значения тригонометрических функций
- Урок 7. Знаки тригонометрических функций
- Урок 8. Чётность и нечётность тригонометрических функций
- Урок 9. Тригонометрические функции некоторых углов
- Урок 10. Построение угла по данному значению его тригонометрической функции
- Урок 11. Основные тригонометрические тождества
- Урок 12. Выражение всех тригонометрических функций через одну из них
- Урок 13. Решение прямоугольных и равнобедренных треугольников с помощью тригонометрических функций
- Урок 14. Теорема синусов
- Урок 15. Теорема косинусов
- Урок 17. Примеры решения задач по планиметрии с применением тригонометрии
- Урок 18. Решение практических задач с помощью тригонометрии
- Урок 19. Формулы приведения (1)
- Урок 20. Формулы приведения (2)
- Урок 21. Формулы сложения и вычитания аргументов тригонометрических функций
- Урок 22. Формулы двойных и тройных углов (аргументов)
- Урок 23. Формулы половинного аргумента
- Урок 24. Формулы преобразования суммы тригонометрических функций в произведение
- Урок 25. Графики функций y = sin x и y = cos x
- Урок 26. Графики функций y = tg x и y = ctg x
- Урок 27. Обратные тригонометрические функции
- Урок 28. Основные тождества обратных тригонометрических функций
- Урок 29. Выражение одной из аркфункций через другие
- Урок 30. Графики обратных тригонометрических функций
- Урок 31. Построение графиков тригонометрических функций методом геометрических преобразований

{S = dfrac{1}{2} cdot a cdot h}
Задача нахождения площади треугольника довольно распространена не только в науке, но и в быту. Для вас мы разработали калькулятор для нахождения площади любого треугольника – равнобедренного, равностороннего, прямоугольного или обыкновенного (разностороннего) по 22 формулам.
- Калькулятор площади треугольника
- Площадь треугольника
- через основание и высоту
- через две стороны и угол между ними
- через сторону и два прилежащих угла
- через радиус описанной окружности и 3 стороны
- через радиус вписанной окружности и 3 стороны
- по формуле Герона
- Площадь прямоугольного треугольника
- через катеты
- через гипотенузу и прилежащий угол
- через катет и прилежащий угол
- через радиус вписанной окружности и гипотенузу
- через вписанную окружность
- по формуле Герона
- через катет и гипотенузу
- Площадь равнобедренного треугольника
- через основание и сторону
- через основание, боковую сторону и угол
- через основание и высоту
- через боковые стороны и угол между ними
- через основание и угол между боковыми сторонами
- Площадь равностороннего треугольника
- через сторону
- через высоту
- через радиус описанной окружности
- через радиус вписанной окружности
- Примеры задач
Площадь треугольника
Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
Площадь треугольника через основание и высоту
{S = dfrac{1}{2} cdot a cdot h}
a – длина основания
h – высота, проведенная к основанию
Площадь треугольника через две стороны и угол между ними
{S = dfrac{1}{2} cdot a cdot b cdot sin(alpha)}
a и b – стороны треугольника
α – угол между сторонами a и b
Площадь треугольника через сторону и два прилежащих угла
{S = dfrac{a^2}{2} cdot dfrac{sin{(alpha)} cdot sin{(beta)}}{sin{(gamma)}}}
{gamma = 180 – (alpha + beta)}
a – сторона треугольника
α и β – прилежащие к стороне a углы
Площадь треугольника через радиус описанной окружности и 3 стороны
{S = dfrac{a cdot b cdot c}{4 cdot R}}
a, b и c – стороны треугольника
R – радиус описанной окружности
Площадь треугольника через радиус вписанной окружности и 3 стороны
{S = r cdot dfrac{a + b + c}{2}}
a, b и c – стороны треугольника
r – радиус вписанной окружности
Площадь треугольника по формуле Герона
{S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)}}
{p= dfrac{a+b+c}{2}}
a, b и c – стороны треугольника
p – полупериметр треугольника
Площадь прямоугольного треугольника
Прямоугольный треугольник — это треугольник, в котором один угол прямой (равен 90 градусов).
Площадь прямоугольного треугольника через катеты
{S = dfrac{1}{2} cdot a cdot b}
a и b – стороны треугольника
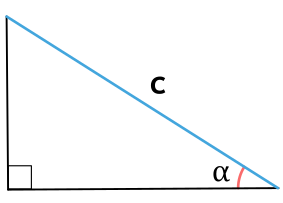
Площадь прямоугольного треугольника через гипотенузу и прилежащий угол
{S = dfrac{1}{4} cdot c^2 cdot sin{(2 alpha)}}
c – гипотенуза прямоугольного треугольника
α – прилежащий к гипотенузе c угол
Площадь прямоугольного треугольника через катет и прилежащий угол
{S = dfrac{1}{2} cdot a^2 cdot tg{(alpha)}}
a – катет прямоугольного треугольника
α – прилежащий к катету a угол
Площадь прямоугольного треугольника через радиус вписанной окружности и гипотенузу
{S = r cdot (r+c)}
r – радиус вписанной окружности
c – гипотенуза прямоугольного треугольника
Площадь прямоугольного треугольника через вписанную окружность
{S = c_1 cdot c_2}
с1 и с2 – отрезки, полученные делением гипотенузы точкой касания окружности
Площадь прямоугольного треугольника по формуле Герона
{S = (p-a) cdot (p-b)}
{p= dfrac{a+b+c}{2}}
a, b и c – стороны треугольника
p – полупериметр треугольника
Площадь прямоугольного треугольника через катет и гипотенузу
{S = dfrac{1}{2} cdot a cdot sqrt{c^2 – a^2}}
a – катет прямоугольного треугольника
c – гипотенуза прямоугольного треугольника
Площадь равнобедренного треугольника
Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине.
Площадь равнобедренного треугольника через основание и сторону
{S = dfrac{b}{4} sqrt{4a^2 – b^2}}
a – боковая сторона равнобедренного треугольника
b – основание равнобедренного треугольника
Площадь равнобедренного треугольника через основание, сторону и угол
{S = dfrac{1}{2} cdot a cdot b cdot sin{(alpha)}}
a – боковая сторона равнобедренного треугольника
b – основание равнобедренного треугольника
α – угол между основанием и боковой стороной
Площадь равнобедренного треугольника через основание и высоту
{S = dfrac{1}{2} cdot b cdot h}
b – основание равнобедренного треугольника
h – высота, проведенная к основанию равнобедренного треугольника
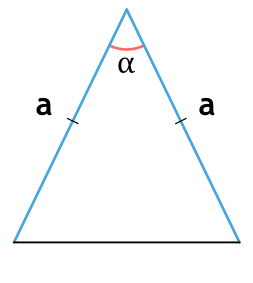
Площадь равнобедренного треугольника через боковые стороны и угол между ними
{S = dfrac{1}{2} cdot a^2 cdot sin(alpha)}
a – боковые стороны равнобедренного треугольника
α – угол между боковыми сторонами
Площадь равнобедренного треугольника через основание и угол между боковыми сторонами
{S = dfrac{b^2}{4 cdot tg {( dfrac{alpha}{2} )}}}
b – основание равнобедренного треугольника
α – угол между боковыми сторонами
Площадь равностороннего треугольника
Равносторонний треугольник – треугольник, у которого все стороны равны.
Площадь равностороннего треугольника через сторону
{S = dfrac{sqrt{3} cdot a^2}{4}}
a – сторона равностороннего треугольника
Площадь равностороннего треугольника через высоту
{S = dfrac{h^2}{sqrt{3}}}
h – высота равностороннего треугольника
Площадь равностороннего треугольника через радиус описанной окружности
{S = dfrac{3 sqrt{3} cdot R^2}{4}}
R – радиус описанной окружности
Площадь равностороннего треугольника через радиус вписанной окружности
{S = 3 sqrt{3} cdot r^2}
r – радиус описанной окружности
Примеры задач на нахождение площади треугольника
Задача 1
Найдите площадь треугольника со сторонами 13 14 15.
Решение
Для решения задачи воспользуемся формулой Герона.
S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)}
Для начала нам необходимо найти полупериметр p:
p= dfrac{a+b+c}{2}p= dfrac{13+14+15}{2}= dfrac{42}{2} = 21
Теперь можем подставить его в формулу Герона и найти ответ:
S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)} = sqrt{21 cdot (21-13) cdot (21-14) cdot (21-15)} = sqrt{21 cdot (8) cdot (7) cdot (6)} = sqrt{21 cdot 336} = sqrt{7056} = 84 : см^2
Ответ: 84 см²
Убедимся в правильности решения с помощью калькулятора .
Задача 2
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 100.
Решение
Воспользуемся формулой.
S = dfrac{1}{2} cdot a cdot sqrt{c^2 – a^2} = dfrac{1}{2} cdot 28 cdot sqrt{100^2 – 28^2} = dfrac{1}{2} cdot 28 cdot sqrt{10000 – 784} = dfrac{1}{2} cdot 28 cdot sqrt{9216} = dfrac{1}{2} cdot 28 cdot 96 = 14 cdot 96 = 1344 : см^2
Ответ: 1344 см²
Проверим ответ на калькуляторе .
Задача 3
Найдите площадь прямоугольного треугольника если его катет и гипотенуза равны соответственно 15 и 17.
Решение
Задача аналогична предыдущей, поэтому решение очень похоже.
S = dfrac{1}{2} cdot a cdot sqrt{c^2 – a^2} = dfrac{1}{2} cdot 15 cdot sqrt{17^2 – 15^2} = dfrac{1}{2} cdot 15 cdot sqrt{289 – 225} = dfrac{1}{2} cdot 15 cdot sqrt{64} = dfrac{1}{2} cdot 15 cdot 8 = 15 cdot 4 = 60 : см^2
Ответ: 60 см²
Проверка .
Задача 4
Найдите площадь прямоугольного треугольника, если гипотенуза его равна 40 см а острый угол равен 60°.
Решение
Для решения задачи воспользуемся формулой.
S = dfrac{1}{4} cdot c^2 cdot sin{(2 alpha)} = dfrac{1}{4} cdot 40^2 cdot sin{(2 cdot 60°)} = dfrac{1}{4} cdot 1600 cdot sin{(120°)} = 400 cdot dfrac{sqrt{3}}{2} = 200 sqrt{3} : см^2 approx 346.41016 : см^2
Ответ: 200 sqrt{3} : см^2 approx 346.41016 : см^2
Проверка .
Задача 5
Найдите площадь равнобедренного треугольника, если боковая сторона равна 7 см а основание 4 см.
Решение
В этой задаче используем формулу для нахождения площади равнобедренного треугольника через основание и боковую сторону.
S = dfrac{b}{4} sqrt{4a^2 – b^2} = dfrac{4}{4} sqrt{4 cdot 7^2 – 4^2} = sqrt{4 cdot 49 – 16} = sqrt{196 – 16} = sqrt{180} = sqrt{36 cdot 5} = 6sqrt{5} : см^2 approx 13.41641 : см^2
Ответ: 6sqrt{5} : см^2 approx 13.41641
Проверка .
Задача 6
Найдите площадь равнобедренного треугольника, если его основание равно 30, боковая сторона равна 17.
Решение
Решим эту задачу по анологии с предыдущей.
S = dfrac{b}{4} sqrt{4a^2 – b^2} = dfrac{30}{4} sqrt{4 cdot 17^2 – 30^2} = dfrac{30}{4} sqrt{4 cdot 289 – 900} = dfrac{30}{4} sqrt{1156 – 900} = dfrac{30}{4} sqrt{256} = dfrac{30}{4} cdot 16= 30 cdot 4 = 120 : см^2
Ответ: 120 см²
Проверка .
Задача 7
Найдите площадь равностороннего треугольника со стороной 12 см.
Решение
Используем для решения задачи формулу.
S = dfrac{sqrt{3} cdot a^2}{4} = dfrac{sqrt{3} cdot 12^2}{4} = dfrac{sqrt{3} cdot 144}{4} = 36 sqrt{3} : см^2 approx 62.35383 : см^2
Ответ: 36 sqrt{3} : см^2 approx 62.35383 : см^2
Проверка .
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона

Формула Герона для нахождения площади треугольника:
– полупериметр треугольника; a,b,c – стороны треугольника.
Через основание и высоту

Формула нахождения площади треугольника с помощью половины его основания и высоту:
a – основание треугольника; h – высота треугольника.
Через две стороны и угол

Формула нахождения площади треугольника через две стороны и угол между ними:
a,b – стороны треугольника; α – угол между сторонами.
Через сторону и два прилежащих угла

Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
<
a– сторона треугольника; α и β – прилежащие углы.
Площадь прямоугольного треугольника

Прямоугольный треугольник – треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
a, b – катеты треугольника.
Площадь равнобедренного треугольника через стороны

Равнобедренный треугольник – треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
a, b – стороны треугольника.
Площадь равнобедренного треугольника через основание и угол

Формула нахождения площади равнобедренного треугольника через основание и угол:
a – основание равнобедренного треугольника; α – угол между сторонами.
Площадь равностороннего треугольника через стороны

Равносторонний треугольник – треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
a – сторона равностороннего треугольника.
Площадь равностороннего треугольника через высоту

Формула нахождения площади равностороннего треугольника через высоту:
h – высота равностороннего треугольника.
Площадь равностороннего треугольника через радиус вписанной окружности

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
r – радиус вписанной окружности равностороннего треугольника.
Площадь равностороннего треугольника через радиус описанной окружности

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
r – радиус описанной окружности равностороннего треугольника.
Площадь треугольника через радиус описанной окружности и три стороны

Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
a, b, c – стороны треугольника; r – радиус описанной окружности треугольника.
Площадь треугольника через радиус вписанной окружности и три стороны

Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
p – полупериметр треугольника;a, b, c – стороны треугольника; r – радиус вписанной окружности треугольника.