Дано:
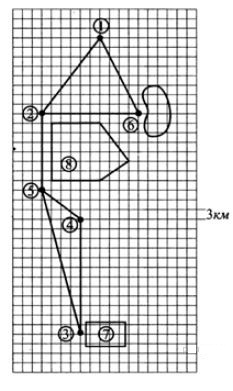
План, на котором я обозначила числа количеством клеток, умноженных на 3 км.
Сначала ребята поехали из точки 1 в точку 6. высчитываем расстояние из прямоугольного треугольника.
Длинная сторона (красная линия) 8 клеток – 8 х 3 = 24 км.
Короткая сторона 4 клетки – 4 х 3 = 12 км.
Гипотенуза равна корню квадратному из суммы квадратов катетов:
√(24² + 12²) = 26.83 километров.
Затем он направились до посёлка Быково, им требуется проехать от точки 6 до точки 2 ещё 30 км. Итог: 26.83 + 30 = 56.83 км.
От Быково до города Гусевск в 5 точку из условия 24 км. Так и есть – 8 клеток по 3 км.
Складываем: 56.83 + 24 = 80.83 км.
Напрямую из точки 5 в точку 3 проехать невозможно – там ремонт дороги. Значит нужно доехать до деревни Астрелка точка 4. А оттуда по прямой до конечного пункта точка 3 кемпинг.
Высчитываем гипотенузу до Астрелки. Длинный катет равен 4 квадрата или 12 км , а короткий 3 квадрата или 9 км:
√(12² + 9²) = √(144 + 81) = √225 = 15 км. Это магический треугольник теоремы Пифагора 3, 4, 5.
Считаем дальше:
80.83 + 15 = 95.83. И прямая до конечного пункта 12 клеток = 36 км. Складываем:
95.83 + 36 = 131.83 км.
Мой ответ ~ 132 километра
Вычисляем площадь заказника: Сначала прямоугольника, потом треугольника и затем их складываем.
Вычисляем площадь прямоугольника: 5 х 3 = 15 метров ширина и 6 х 3 = 18 длина.
Площадь равна 15 х 18 = 270 м²
Вычисляем площадь треугольника: Основание равно 6 х 3 = 18 метров; Высота равна 3 х 3 = 9 метров.
Вычисляем площадь треугольника:
(18 х 9)/2 = 81 м²
Складываем: 270 + 81 = 351 м²
Площадь заказника равна 351 м²
0
айдите площадь (в км2), которую занимает заказник.
Андрей и его друзья собираются поехать в отпуск на две недели. Предварительно они наметили маршрут, представленный на рисунке. Они планируют на велосипедах добраться от города Гранюк до кемпинга, обозначенного на рисунке цифрой 7, за 4 дня, а потом поставить там палатки и отдыхать в море. Друзья собираются выехать рано утром и в первый день добраться до хутора Южный, где живёт бабушка Андрея. Там есть озеро, в котором можно купаться и ловить рыбу, что они и собираются делать до обеда следующего дня. Потом планируется доехать до посёлка Быково и заночевать там в мини‐отеле. На следующий день они собираются проехать 24 км до города Гусевск вдоль степного заказника и переночевать в одной из гостиниц. Заказник обозначен на рисунке цифрой 8. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Прямой путь короче, но там в эти дни идёт ремонт дороги, и пока неизвестно, где можно будет проехать быстрее.
1 ответ:
0
0
Сначала найдем площадь квадрата 5*6=30,потом треугольника 1/2*6*3=9,теперь общая площадь 30+9=39
Читайте также
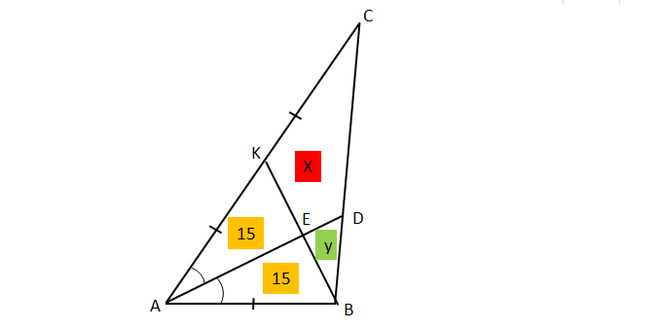
На рисунке, предоставленном автором вопроса, треугольник искаженный и не соответствует условию. По этой причине предлагаю свой вариант рисунка.
Биссектриса угла треугольника делит противоположную сторону на части пропорциональные к прилежащим к ней сторонам. Следовательно согласно условия АВ : АС = 1 :2. Тогда АК = АВ, а треугольник АКВ равносторонний и биссектриса АD делит его на равные части. В свою очередь медиана ВК делит треугольник АСВ на два равновеликих треугольника. Откуда площади треугольников АКЕ и АЕВ составляют по 15 кв. см.
Биссектриса треугольника делит так же площадь треугольника пропорционально прилежащим к ней сторонам. Тогда площади треугольников АDВ и АСD относятся друг к другу как 1 : 2.
На основании сказанного составим систему уравнений, обозначив неизвестные площади треугольников за х и у,
{х + у = 15
{15 + х = 2(15 + У).
Решая систему относительно х, получаем – площадь 4-угольника EDCK равна 25 кв. см.
<h2>Основной государственный экзамен по математике 2015.</h2>
ОГЭ по математике это экзамен который сдают девятиклассники, по сути это подготовка к сдаче экзамена ЕГЭ. Еще в прошлом году ОГЭ назывался ГИА (государственная итоговая аттестация), но в этом году изменили название (по аналогии с ЕГЭ), по сути изменилось только название, порядок проведения и правила остались такие же как и раньше. В 2015 году ОГЭ по математике состоится 27 мая. Минимальное количество баллов которое необходимо набрать чтобы продолжить обучение или получить аттестат – 8 баллов.
Если Вы сдали остальные предметы лучше чем математику, то снова пересдать Вы, естественно, можете в этом году через месяц – в сентябре. Но лучше хорошенько подготовиться, решать побольше КИМов в течении августа и, наконец, сдать математику, не завалив алгебру. ОГЭ в 9 классе очень важно для дальнейшей учебы в целом, так что постарайтесь сделать это как можно лучше.
Насколько мне известно, если Вы не сдадите этот экзамен в сентябре, то передавать будете уже в следующем году вместо с будущими девятиклассниками.
Желаю Вам сдать как можно лучше уже через месяц 🙂
Такие задания появились в новой демоверсии ОГЭ по математике. Большинство изменений коснулись именно заданий с геометрическим содержанием. Для выполнения данного конкретного задания выпускнику 9 класса необходимо вспомнить теорему о параллельной прямой, проходящей через точку не лежащую на данной прямой, о неравенстве треугольников и свойства параллелограмма, то есть теоретические знания. Так через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой (и только одну) – это предложение верное. Сумма двух сторон треугольника всегда больше третьей стороны, значит предложение “Треугольник со сторонами 1,2,4 существует” неверное, так как 1+2 < 4. У параллелограмма противоположные углы равны, значит предложение “В любом параллелограмме есть два равных угла” верное. Ответ: 12.
Допустим, третий велосипедист догнал второго через х часов, второй велосипедист к этому времени находился в пути уже (х + 1) час, значит, второй и третий спортсмен встретились в 12(х + 1) км от старта, а скорость третьего в этом случае составляет 12(х + 1)/х км/ч.
С момента старта первого велосипедиста до момента встречи его с третьим прошло (х + 10) часов, а значит, их встреча произошла в 22(х + 10) км от старта. Это расстояние третий спортсмен преодолел за 22х(х + 10)/12(х + 1) или (11х² + 110)/(6х + 6) часов, что по условию на 2 часа меньше, чем потребовалось первому спортсмену. Таким образом,
х + 10 – (11х² + 110х)/(6х + 6) = 2, или
5х² + 56х – 48 = 0.
Единственным положительным корнем данного уравнения явл-ся х = 0,8. В этом случае скорость третьего спортсмена 12*(0,8 + 1)/0,8 = 27 км/ч.
Вариант № 9
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на рисунке. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
|
Объекты |
Город Гранюк |
Деревня Астрелка |
Хутор Южный |
Город Гусевск |
|
Цифры |
Андрей и его друзья собираются поехать в отпуск на две недели. Предварительно они наметили маршрут, представленный на рисунке. Они планируют на велосипедах добраться от города Гранюк до кемпинга, обозначенного на рисунке цифрой 7, за 4 дня, а потом поставить там палатки и отдыхать в море. Друзья собираются выехать рано утром и в первый день добраться до хутора Южный, где живёт бабушка Андрея. Там есть озеро, в котором можно купаться и ловить рыбу, что они и собираются делать до обеда следующего дня. Потом планируется доехать до посёлка Быково и заночевать там в мини‐отеле. На следующий день они собираются проехать 24 км до города Гусевск вдоль степного заказника и переночевать в одной из гостиниц. Заказник обозначен на рисунке цифрой 8. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Прямой путь короче, но там в эти дни идёт ремонт дороги, и пока неизвестно, где можно будет проехать быстрее.
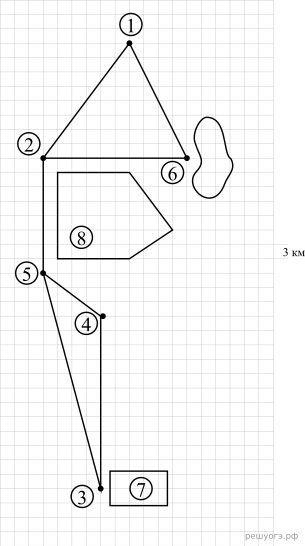
Решение. Андрей и его друзья собираются начинать движение из города Гранюк, следовательно, он отмечен на рисунке цифрой 1. Рядом с хутором Южный расположено озеро. Значит, хутор Южный отмечен на рисунке цифрой 6. После хутора Южный планируется поехать до посёлка Быково, а потом проехать до города Гусевска вдоль степного заказника. Значит, город Гусевск обозначен на рисунке цифрой 5. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Значит, деревня Астрелка обозначена на рисунке цифрой 4.
Ответ: 1465.
2. Ребята решили, что нужно взять в поездку чай в пакетиках определённого сорта. Оксане поручили купить чай на всех. Сколько пачек чая должна купить Оксана, если в компании 8 человек, в день они выпивают в среднем 3 пакетика на одного человека и поездка продлится две недели? В каждой пачке 25 пакетиков чая.
Решение. Найдём, сколько пакетиков чая ребята потратят за две недели:
Значит, им понадобится
пачек чая.
Таким образом, ребята должны купить 14 пачек чая.
Ответ: 14.
3. Найдите площадь (в км2), которую занимает заказник.
Решение. 
Ответ: 351.
4. Все могут пойти в отпуск с 15 июля, кроме Григория и Марии, которым в этот день нужно работать. Они готовы выехать 16 июля и догнать остальную группу в посёлке Быково, не заезжая на хутор Южный. Найдите расстояние, которое проедут Григорий и Мария от города Гранюк до Быково. Ответ дайте в километрах.
Решение. Найдём расстояние, которое проедут Григорий и Мария от города Гранюк до Быково, по теореме Пифагора:
км.
Ответ: 30.
5. Андрей выяснил, что его велосипед пришёл в нерабочее состояние. Андрей посетил сайты интернет‐магазина «ОК» и магазина «Вело», расположенного в соседнем доме, чтобы узнать некоторые цены. В этих магазинах можно купить готовый велосипед либо запасные части. Цены на продукцию магазинов и срок доставки из интернет‐магазина даны в таблице.
|
Продукция |
Цена в магазине |
Цена в магазине |
Срок доставки из |
|
Подсветка для спиц |
190 |
180 |
3 |
|
Шина вида «А» |
680 |
650 |
12 |
|
Шина вида «Б» |
1680 |
1450 |
12 |
|
Спица |
70 |
80 |
3 |
|
Педаль вида «А» |
437 |
405 |
10 |
|
Педаль вида «Б» |
860 |
750 |
10 |
|
Тормоз вида «А» |
1130 |
нет |
10 |
|
Тормоз вида «Б» |
нет |
2180 |
10 |
|
Набор крепёжных изделий |
740 |
765 |
14 |
Андрея не устраивает срок доставки деталей из интернет‐магазина, и он решил приобрести детали в магазине «Вело». Он готов потратить на ремонт не более 6000 рублей и при этом хочет купить самый дорогой набор для ремонта велосипеда, который может себе позволить. Ему нужно купить 5 спиц, 2 шины (одного вида), 2 педали (одного вида), тормоз (любого вида) и набор крепёжных изделий. Сколько рублей Андрей потратит на набор запасных частей?
Решение. На спицы Андрей потратит 70 · 5 = 350 руб. Далее, Андрей должен купить две шины вида «А», поскольку если он купит две шины вида «Б», ему не хватит денег на остальные запчасти. Значит, на шины он потратит 680 · 2 = 1360 руб. Поскольку Андрей хочет купить самый дорогой набор для ремонта велосипеда, из двух видов педалей он может купить педали вида «Б», они будут стоить 860 · 2 = 1720 руб. Ему останется купить тормоз и набор крепёжных изделий. Таким образом, всего Андрей потратит:
руб.
Ответ: 5300.
Приведем другое решение.
Спицы, тормоз и набор крепежных изделий в магазине имеются только одного вида. На них Андрей потратит
руб.
Следовательно, у него останется 6000 − 2220 = 3780 руб.
Если Андрей купит шины вида «Б», то он потратит на них 2 · 1680 = 3360 руб. и у него не останется денег на педали. Следовательно, Андрей должен купить шины вида «А». На них он потратит 2 · 680 = 1360 руб. и для покупки педалей останется еще 3780 − 1360 = 2420 руб. Следовательно, Андрей может купить педали вида «Б». На них он потратит 2 · 860 = 1720 руб. Общая сумма покупок составит
руб.
6. Найдите значение выражения
Решение. Выполним умножение, затем сложение:
Ответ: 24,52.
7. На координатной прямой отмечены числа a, b, и c.
В ответе укажите номер правильного варианта.
Укажите номер верного утверждения.
1)
2)
3)
4)
Решение. Заметим, что откуда
Рассмотрим каждое утверждение:
1) — неверно.
2) — неверно.
3) — неверно.
4) — верно.
Правильный ответ указан под номером: 4.
8. Найдите значение выражения
Решение. Вычислим:
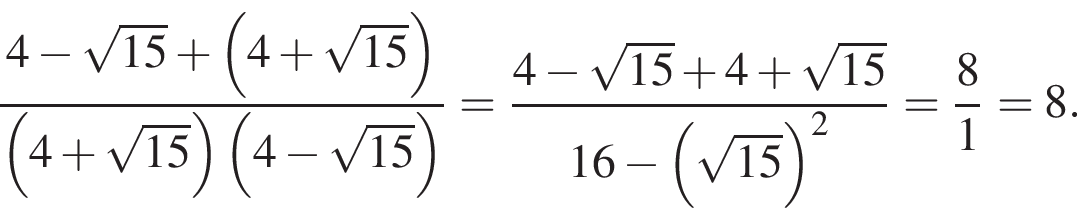
Ответ: 8.
9. Решите уравнение
Решение. Последовательно получаем:
Ответ: 7.
10. В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.
Решение. Всего спортсменов 11 + 6 + 3 = 20 человек. Поэтому вероятность того, что первым будет стартовать спортсмен не из России равна
Ответ: 0,45.
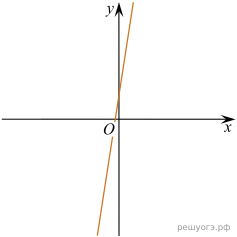
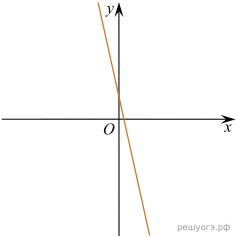
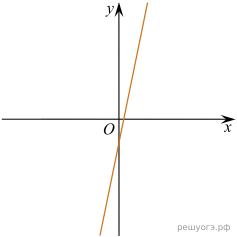
11. На рисунке изображены графики функций вида y = kx + b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
Графики
|
А)
|
Б)
|
В)
|
Коэффициенты
|
1) k b 0 |
2) k 0, b 0 |
3) k b |
4) k 0, b |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
В |
Решение. Если прямая задана уравнением то при
функция возрастает, при
— убывает. Значению b соответсвует значение функции в точке
Таким образом, графику A соответствуют коэфициенты 2, Б − 1, В − 4.
Ответ: 214.
12. Площадь любого выпуклого четырехугольника можно вычислять по формуле , где
— длины его диагоналей, а
угол между ними. Вычислите
, если
.
Решение. Выразим :
Подставляя, получаем:
Ответ: 0,4.
13. На каком рисунке изображено множество решений неравенства ?
|
1)
|
2)
|
|
3)
|
4)
|
Решение. Решим неравенство:
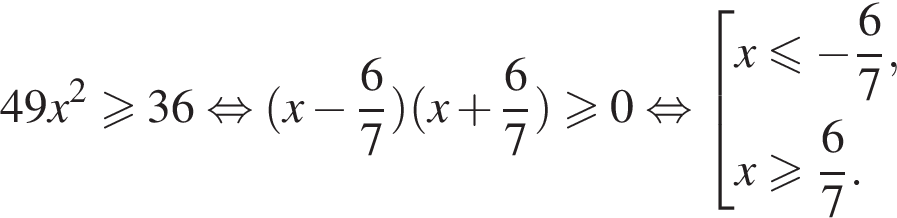
Ответ: 4.
14. Турист идет из одного города в другой, каждый день проходя больше, чем в предыдущий день, на одно и то же расстояние. Известно, что за первый день турист прошел 10 километров. Определите, сколько километров прошел турист за третий день, если весь путь он прошел за 6 дней, а расстояние между городами составляет 120 километров.
Решение. В первый день турист прошел км, во второй —
…, в последний —
км. Всего он прошел
км. Если каждый день турист проходил больше, чем в предыдущий день, на d км, то
где дней,
км. Таким образом,
Тогда за третий день турист прошел
Ответ: 18.
15. 
Решение. Углы А и В — односторонние, поэтому угол В равен 180° − 45° − 30° = 105°.
Ответ: 105.
16.
Найдите ∠DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно.
Решение. Дуга FD, не содержащая точку Е, равна 360° − 150° − 68° = 142°, поэтому ∠DEF = 71°.
Ответ: 71.
17. 
Решение. Площадь параллелограмма равна произведению высоты на основание, поэтому она равна
Ответ: 20.
18. 
Решение. Посчитаем количество клеток внутри закрашенной области: их 9.
Ответ: 9.
19. Какие из следующих утверждений верны?
1) Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.
2) Боковые стороны любой трапеции равны.
3) Один из углов треугольника всегда не превышает 60 градусов.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Решение. Рассмотрим каждое из утверждений:
1) «Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне» — верно, так как ромб — это частный случай параллелограмма и его площадь есть произведение его стороны на высоту, проведённую к этой стороне.
2) «Боковые стороны любой трапеции равны» — неверно, боковые стороны равнобедренной трапеции равны.
3) «Один из углов треугольника всегда не превышает 60 градусов» — верно, наименьший угол в любом треугольнике всегда не превышает 60 градусов.
Ответ: 13
20. Решите неравенство
Решение. Решим неравенство методом интервалов, для этого, сначала разложим на множители выражение
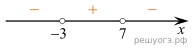
Теперь расставим точки на прямой и определим знаки выражения на каждом получившемся промежутке (см. рис.).
Таким образом, ответ
Ответ:
Примечание.
Обратите внимание, что при определении знаков выражения используется исходное выражение, а именно,
21. Имеются два сосуда, содержащие 40 кг и 30 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 73% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 72% кислоты. Сколько килограммов кислоты содержится во втором растворе?
Решение. Пусть концентрация первого раствора – х, концентрация второго раствора – y. Составим систему уравнений согласно условию задачи:
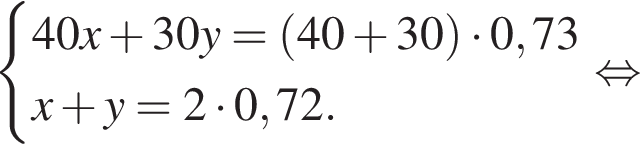
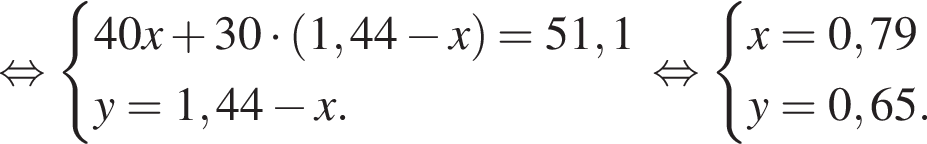
Таким образом, во втором растворе содержится килограмма кислоты
Ответ: 19,5
22. Известно, что графики функций и
имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
Решение. Найдём абсциссы точек пересечения:
Графики функций, будут иметь ровно одну точку пересечения, если это уравнение имеет ровно одно решение. То есть, если дискриминант этого квадратного уравнения будет равен нулю.
Подставив параметр p в уравнение, найдём x координату точки пересечения этих функций:
Координата y находится путём подстановки координаты x в любое из уравнений, например, во второе:
Теперь, зная p, можем построить графики обеих функций (см. рис.).
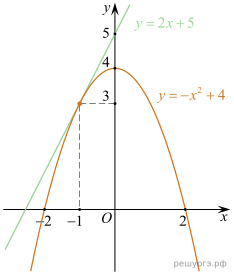
Ответ: (−1; 3).
23.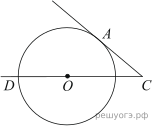
Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 140° .
Решение. 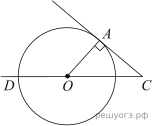
Угол AOD — центральный, следовательно, он равен величине дуги, на которую опирается,
Угол DOC — развёрнутый, следовательно,
Из треугольника AOC,
Ответ: 50°.
24. В параллелограмме KLMN точка B — середина стороны KN. Известно, что BL = BM. Докажите, что данный параллелограмм — прямоугольник.
Решение. 
Рассмотрим треугольники KLB и BMN, в них KB равно BN, LB равно BM и KL равно MN, следовательно, треугольники равны по трём сторонам, а значит,
Вспомним также, что противоположные углы параллелограмма равны, следовательно:
Сумма углов параллелограмма 360°:
Все углы параллелограмм прямые, а следовательно, этот параллелограмм — прямоугольник.
25. В треугольнике ABC угол равен 120°, а длина стороны AB на
меньше полупериметра треугольника. Найдите радиус окружности, касающейся стороны BC и продолжений сторон AB и AC.
Решение. Центр окружности является точкой пересечения биссектрис углов CBM и BCL. При этом по свойству касательных . Следовательно, длины ломаных ACK и ABK равны полупериметру p. По условию
.

Найдем радиус KO из прямоугольного треугольника BKO. В треугольнике BKO
катет KO лежит против угла 30°, значит,
Ответ: 3.
|
№ задания |
ответ |
|
1 |
1465 |
|
2 |
14 |
|
3 |
351 |
|
4 |
30 |
|
5 |
5300 |
|
6 |
24,52 |
|
7 |
4 |
|
8 |
8 |
|
9 |
7 |
|
10 |
0,45 |
|
11 |
214 |
|
12 |
0,4 |
|
13 |
4 |
|
14 |
18 |
|
15 |
105 |
|
16 |
71 |
|
17 |
20 |
|
18 |
9 |
|
19 |
13 |
|
20 |
|
|
21 |
19,5 |
|
22 |
(−1; 3). |
|
23 |
50 |
|
24 |
– |
|
25 |
3 |
Дано:
План, на котором я обозначила числа количеством клеток, умноженных на 3 км.
Сначала ребята поехали из точки 1 в точку 6. высчитываем расстояние из прямоугольного треугольника.
Длинная сторона (красная линия) 8 клеток — 8 х 3 = 24 км.
Короткая сторона 4 клетки — 4 х 3 = 12 км.
Гипотенуза равна корню квадратному из суммы квадратов катетов:
√(24² + 12²) = 26.83 километров.
Затем он направились до посёлка Быково, им требуется проехать от точки 6 до точки 2 ещё 30 км. Итог: 26.83 + 30 = 56.83 км.
От Быково до города Гусевск в 5 точку из условия 24 км. Так и есть — 8 клеток по 3 км.
Складываем: 56.83 + 24 = 80.83 км.
Напрямую из точки 5 в точку 3 проехать невозможно — там ремонт дороги. Значит нужно доехать до деревни Астрелка точка 4. А оттуда по прямой до конечного пункта точка 3 кемпинг.
Высчитываем гипотенузу до Астрелки. Длинный катет равен 4 квадрата или 12 км , а короткий 3 квадрата или 9 км:
√(12² + 9²) = √(144 + 81) = √225 = 15 км. Это магический треугольник теоремы Пифагора 3, 4, 5.
Считаем дальше:
80.83 + 15 = 95.83. И прямая до конечного пункта 12 клеток = 36 км. Складываем:
95.83 + 36 = 131.83 км.
Мой ответ ~ 132 километра
Вычисляем площадь заказника: Сначала прямоугольника, потом треугольника и затем их складываем.
Вычисляем площадь прямоугольника: 5 х 3 = 15 метров ширина и 6 х 3 = 18 длина.
Площадь равна 15 х 18 = 270 м²
Вычисляем площадь треугольника: Основание равно 6 х 3 = 18 метров; Высота равна 3 х 3 = 9 метров.
Вычисляем площадь треугольника:
(18 х 9)/2 = 81 м²
Складываем: 270 + 81 = 351 м²
Площадь заказника равна 351 м²
Увеличение числа и мощности природных катаклизмов (засух, лесных пожаров, наводнений, снегопадов) заставляет все большее количество людей задуматься о причинах, вызывающих природные катастрофы. Ученые однозначно указывают на глобальное потепление, изменяющее термодинамические процессы экосистемы планеты. Для замедления глобального потепления разрабатывается ряд мер. Одной из них является сохранение естественных природных экосистем – создание системы особо охраняемых природных территорий (ООПТ). Подробнее эту тему рассмотрит в статье наш преподаватель географии Татьяна Валентиновна.
Природа России разнообразна и уникальна. Её бескрайние просторы вносят невосполнимый вклад в сохранение устойчивости экологического баланса планеты. О мировом значении природы России говорит статус объектов Всемирного природного наследия. Такой статус на территории России имеют одиннадцать объектов, куда входят 13 заповедников, 7 национальных парков, 3 федеральных заказника, несколько памятников природы и буферные зоны заповедников. К ним относятся:
- «Девственные леса Коми». Под охраной находятся предгорные и горные темнохвойные таёжные леса. Состав: Печоро-Илычский заповедник и национальный парк «Югыдва».
- «Озеро Байкал». Под охраной находятся акватория оз. Байкал, прилегающие горные хребты, уникальный животный мир: байкальский омуль и нерпа (байкальский тюлень), кабарга, марал, соболь. Состав: заповедники Байкальский, Баргузинский, Байкало-Ленский, национальные парки Прибайкальский, Забайкальский и Тункинский (частично), заказники Кабанский и Фролихинский.
- «Вулканы Камчатки». Состав: Кроноцкий заповедник и Южно-Камчатский заказник.
- «Золотые горы Алтая». Под охраной находятся на относительно небольшой площади соседство очень контрастных ландшафтов – хвойных лесов, горных степей, лугов и тундр, высокогорных ледников, на самом юге — полупустыни. Состав: Алтайский и Катунский заповедники.
- «Западный Кавказ». Под охраной находятся самый крупный горно-лесной резерват Европы. Состав: Кавказский государственный заповедник, Сочинский национальный парк, Природный парк Большой Тхач, памятники природы «Хребет Буйный», «Верховье реки Цица», «Верховье рек Пшеха и Пшехашха».
- «Центральный Сихотэ-Алинь». Состав: Сихотэ-Алинский заповедник и национальный парк «Бикин».
- «Остров Врангеля». Состав: заповедник «Остров Врангеля«.
- «Убсунурская котловина». Состав: заповедник «Убсунурская котловина» Под охраной находится экосистема озера Убсу-нур.
- «Плато Путорана». Под охраной находятся нетронутая тайга, лесотундра, тундра, арктические пустыни. Состав: Путоранский заповедник.
- «Ленские столбы». Здесь охраняются редкой красоты скальные образования, которые достигают в высоту около 100 метров и располагаются вдоль берега реки Лена в центральной части республики Саха (Якутия). Состав: национальный парк «Ленские столбы».
- «Ландшафты Даурии». Охраняются экосистемы даурской степи, которая начинается на востоке Монголии и простирается через российскую Сибирь до северо-восточной границы Китая. Состав: Даурский заповедник.
Всего в России по состоянию на 1 января 2017 года насчитывалось около 12 тысяч ООПТ федерального, регионального и местного значения. Федеральное значение имеют 296 ООПТ, в том числе 103 государственных природных заповедников, 49 национальных парков и 59 государственных природных заказников, а также 17 памятников природы и прочие ООПТ федерального значения.
Тема охраны природы нашла отражение в тестовых материалах ОГЭ. Задание предусматривает выбор, из предложных четырех вариантов ответов заповедника, соответствующего описанию условия. Чаще всего в заданиях упоминаются следующие объекты.
Астраханский природный биосферный заповедник располагается в дельте реки Волги в Астраханской области. Главными объектами охраны являются лотос, чилим, рдест, рогоз, валлиснерия. Здесь останавливаются на пролёте белые журавли — стерхи, — одни из самых редких птиц на планете. Так же здесь гнездятся кудрявые пеликаны, малые бакланы, колпицы, египетские цапли. Среди рыб под охраной находятся белуга, осётр, севрюга.
Кивач – один из самых первых заповедников России, центральным объектом, которого является одноимённый водопад. Водопад располагается на реке Суна в Карелии. Рельеф территории создан древним ледником, обработавшим кристаллические породы Балтийского щита. Поэтому здесь стремительное течение водных потоков, наличие водопадов, а в низинах между кристаллическими грядами (сельгами) расположены малые лесные озёра-ламбы. Стремительный водный поток окружен тайгой, возраст некоторых деревьев достигает до 300 лет.
Командорский заповедник располагается на востоке России, в северной части Тихого океана. Здесь охраняются уникальные лежбища морских млекопитающих: каланов (морской бобр), командорского ремнезуба (китообразное млекопитающее), антура (островной тюлень), малого полосатика (вид китов). Из птиц — белоголовый орлан, кречет, сапсан. На территории заповедника существуют объекты исторического и культурного наследия: Стоянка экспедиции Витуса Беринга в 1741—1742 годах с могилой Беринга.
Тунгусский заповедник – располагается в районе реки Подкаменной Тунгуски (Красноярский край) в природной зоне тайги.
Большой Арктический заповедник состоит из семи участков. Находится на полуострове Таймыр. Охраняется экосистема арктической пустыни переходящая в тундру.
Гыданский заповедник занимает северную часть Гыданского полуострова и прилегающие острова. Под охраной находятся экосистема арктической пустыни с популяциями дикого северного оленя, белого медведя, белоклювой гагары, краснозобой казарка, орлана-белохвоста, сапсана, белой чайки.
По характеру растительности территория Оренбургского заповедника входит в Евроазиатскую степную область. Охраняется степная растительность, лошадь Пржевальского, сайгаки, орлан белохвост, обыкновенный фламинго и др.
В Сихоте-Алинском заповеднике (Приморский край) охраняются малонарушенные горные экосистемы Дальнего Востока, а также редкие видов фауны: гималайский медведь и амурский тигр.
Приокско-Террасный (Московская область). Объект охраны – приокские боры с участками широколиственных лесов, в подлески которых произрастают степные виды. То есть здесь происходит переход смешанных лесов в степь.
На Камчатке в Кроноцком заповеднике расположены 8 действующих вулканов, высочайшим из которых является Кроноцкая Сопка, термальные озера, знаменитая Долина гейзеров, водопады. Основную часть территории заповедника занимают леса из каменной берёзы (березы Эрмана), в верхних частях склонов гор распространены заросли кедрового и ольхового стланика.
Ильме́нский заповедник называют «музеем в природе». Здесь можно в природе найти около 200 видов минералов. В пегматитовых жилах, встречаются топазы, аквамарины, цирконы, сапфиры, турмалины, амазониты.
Всего в ответах тестовых заданий используется более 50 названий ООПТ. Особенности всех заповедников и национальных парков знать сложно. Тем более повторить перед экзаменом. Поэтому можно воспользоваться алгоритм рассуждения при ответе на тестовое задание.
- Необходимо хорошо выучить характеристику природных зон: особенности климата, растительности, животного мира, почв.
- Знать названия географических объектов: форм рельефа, рек, остовов, полуостровов и других, т.к. многие названия ООПТ получили от географических объектов, где они располагаются.
- Сопоставить карту природных зон и карту ООПТ: найти на карте указанные в задании заповедники или национальные парки, выбрать тот заповедник, который располагается на территории природной зоны, характеристика, которой указана в условии задания.
Например:
Учёные-биологи должны исследовать места обитания популяций овцебыков, белых медведей, некоторых видов птиц. Какой из перечисленных заповедников им следует посетить для проведения исследовательской работы?
|
1) |
«Остров Врангеля» |
|
2) |
Магаданский |
|
3) |
Командорский |
|
4) |
Печоро-Илычский |
Рассуждение. Белые медведи и овцебыки обитают в зоне арктических пустынь. Рассмотрим расположение заповедников: Магаданский – зона тайги и область высотной поясности, Командорский – тундра, морская акватория, Печоро-Илычский – тайга, «Остров Врангеля» — зона арктических пустынь. Правильный ответ – 1) «Остров Врангеля.
Кроме того, стоит знать и особенности территориальной дифференциации природной зоны. Например.
Студенты естественно-географического факультета исследуют видовой состав елово-лиственничных лесов с элементами маньчжурской флоры и распространение зарослей кедрового стланика. Какой из перечисленных заповедников им следует посетить?
|
1) |
Воронежский |
|
|
2) |
Зейский |
|
|
3) |
Гыданский |
|
|
4) |
Астраханский |
Здесь надо знать, что маньчжурская флора произрастает на Дальнем Востоке. Ответ –2) Зейский, который располагается на Дальнем Востоке.
Таким образом, знания по теме «Особо охраняемые природные территории» поможет не только в решении тестовых заданий, но в таком важном деле как сохранение природы и жизни на планете Земля.
Примечание
* жирным шрифтом обозначены особо охраняемые территории, которые упоминаются в тестовых заданиях.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
д)Периметр равнобедренного треугольника равен 392, а боковая сторона – 100. Найдите площадь треугольника.
4. А)В прямоугольном треугольнике гипотенуза равна 70, а один из острых углов равен 45∘. Найдите площадь треугольника.
б) В прямоугольном треугольнике гипотенуза равна 82, а один из острых углов равен 45∘. Найдите площадь треугольника.
в) В прямоугольном треугольнике гипотенуза равна 8, а один из острых углов равен 45∘. Найдите площадь треугольника
г)В прямоугольном треугольнике один из катетов равен 7, а острый угол, прилежащий к нему, равен 45∘. Найдите площадь треугольника.
5.а)В треугольнике со сторонами 16 и 2 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
б) В треугольнике со сторонами 15 и 3 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
в) В треугольнике со сторонами 2 и 4 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 2. Чему равна высота, проведённая ко второй стороне?
6. а). Площадь равнобедренного треугольника равна 196√3. Угол, лежащий напротив основания, равен 120∘. Найдите длину боковой стороны.
Б) Площадь равнобедренного треугольника равна 625√3. Угол, лежащий напротив основания, равен 120∘ 3. Найдите длину боковой стороны.
В) Площадь равнобедренного треугольника равна 4√3. Угол, лежащий напротив основания, равен, 120∘. Найдите длину боковой стороны.
Б) Площадь прямоугольного треугольника равна . Один из острых углов равен 60∘. Найдите длину катета, лежащего напротив этого угла.
В) Площадь прямоугольного треугольника равна Один из острых углов равен 60∘. Найдите длину катета, лежащего напротив этого угла.
Г) Площадь прямоугольного треугольника равна 882√ 3. Один из острых углов равен 60∘. Найдите длину катета, прилежащего к этому углу.
Д) Площадь прямоугольного треугольника равна 512√3. Один из острых углов равен 30∘. Найдите длину катета, лежащего напротив этого угла.
е) Площадь прямоугольного треугольника равна 722√3. Один из острых углов равен 30∘. Найдите длину катета, лежащего напротив этого угла.
ё)Площадь прямоугольного треугольника равна . Один из острых углов равен 30∘. Найдите длину катета, прилежащего к этому углу.
ж)Площадь прямоугольного треугольника равна 50√3. Один из острых углов равен 60∘. Найдите длину катета, прилежащего к этому углу.
з) Площадь прямоугольного треугольника равна 2450√3/3. Один из острых углов равен 30∘. Найдите длину катета, прилежащего к этому углу
е) Площадь прямоугольного треугольника равна 50√3. Один из острых углов равен 30∘. Найдите длину гипотенузы.
-
7. Найдите площадь трапеции, изображённой на рисунке.
8.а) Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 6.
б)
- Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 5.
9.а) В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 4. Найдите площадь трапеции.
б)В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 2. Найдите площадь трапеции.
10.а) Боковые стороны AB и CD трапеции ABCD равны соответственно 36 и 39, а основание BC равно 12. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
б) Боковые стороны AB и CD трапеции ABCD равны соответственно 24 и 30, а основание BC равно 6. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
11.а)Основания трапеции равны 1 и 13, одна из боковых сторон равна 15√2, а угол между ней и одним из оснований равен 135∘. Найдите площадь трапеции.
- б)Основания трапеции равны 6 и 20, одна из боковых сторон равна 13√2, а угол между ней и одним из оснований равен 135∘. Найдите площадь трапеции.
в)Основания трапеции равны 6 и и 10, одна из боковых сторон равна 23√2, а угол между ней и одним из оснований равен 135∘. Найдите площадь трапеции.
12.а) Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
13.а) б)Найти площадь трапеции
-
14.а) Основания равнобедренной трапеции равны 2 и 14, а её боковые стороны равны 10. Найдите площадь трапеции.
б) Основания равнобедренной трапеции равны 8 и 18, а её боковые стороны равны 13. Найдите площадь трапеции.
- в)Основания равнобедренной трапеции равны 5 и 15, а её боковые стороны равны 13. Найдите площадь трапеции.
15.а) В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
б) В равнобедренной трапеции основания равны 4 и 8, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
16. Найдите площадь параллелограмма
-
17.а)Площадь параллелограмма ABCD равна 6. Точка E – середина стороны AB. Найдите площадь трапеции EBCD.
-
б)Площадь параллелограмма ABCD равна 30. Точка E – середина стороны CD. Найдите площадь трапеции ABED.
-
в)Площадь параллелограмма ABCD равна 140. Точка E – середина стороны AD. Найдите площадь трапеции AECB.
18.а) а Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=19, а расстояние от точки K до стороны AB равно 7.
б)Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=11, а расстояние от точки K до стороны AB равно 3.
в)Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=12, а расстояние от точки K до стороны AB равно 9.
19.а) 26. Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=63. Диагональ параллелограмма BD равна 65. Найдите площадь параллелограмма.
- б)Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=8 и HD=40. Диагональ параллелограмма BD равна 50. Найдите площадь параллелограмма.
- в)Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=7 и HD=24 Диагональ параллелограмма BD равна 51. Найдите площадь параллелограмма.
20.а) Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=19, а расстояние от точки K до стороны AB равно 7.
б)Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=11, а расстояние от точки K до стороны AB равно 3.
в)Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=12, а расстояние от точки K до стороны AB равно 9.
- 21.а) Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
- б) Сторона ромба равна 18, а расстояние от центра ромба до неё равно 5. Найдите площадь ромба.
22.а) Площадь ромба равна 27, а периметр равен 36. Найдите высоту ромба.
-
б) Площадь ромба равна 54, а периметр равен 36. Найдите высоту ромба.
-
в)Площадь ромба равна 15, а периметр равен 20. Найдите высоту ромба.
-
г) Площадь ромба равна 72, а периметр равен 36. Найдите высоту ромба.
- д) Площадь ромба равна 48, а периметр равен 32. Найдите высоту ромба.
- 23.а) Периметр ромба равен 116, а один из углов равен 30∘. Найдите площадь ромба.
- б) Периметр ромба равен 60, а один из углов равен 30∘. Найдите площадь ромба.
- в) Периметр ромба равен 32, а один из углов равен 30∘. Найдите площадь ромба.
24.а) Найдите площадь ромба, если его диагонали равны 14 и 6.
б) Найдите площадь ромба, если его диагонали равны 45 и 2.
в) Найдите площадь ромба, если его диагонали равны 4 и 6.
25.а) Сторона ромба равна 50, а диагональ равна 80. Найдите площадь ромба.
б) Сторона ромба равна 29, а диагональ равна 42. Найдите площадь ромба.
в) Сторона ромба равна 65, а диагональ равна 104. Найдите площадь ромба.
-
26.а) Периметр квадрата равен 160. Найдите площадь квадрата.
- б)Периметр квадрата равен 60. Найдите площадь квадрата
27.а). Площадь прямоугольного земельного участка равна 11 га, ширина участка равна 100 м. Найдите длину этого участка в метрах.
б) Площадь прямоугольного земельного участка равна 20 га, ширина участка равна 200 м. Найдите длину этого участка в метрах.
28.а)Найдите площадь квадрата, если его диагональ равна 20.
- б)Найдите площадь квадрата, если его диагональ равна 50
29.а)Картинка имеет форму прямоугольника со сторонами 19 см и 32 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 1080 см2. Какова ширина окантовки? Ответ дайте в сантиметрах
б)Картинка имеет форму прямоугольника со сторонами 20 см и 23 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 1258 см2. Какова ширина окантовки? Ответ дайте в сантиметрах.
30. Пол комнаты, имеющей форму прямоугольника со сторонами 4 м и 9 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 25 см. Сколько потребуется таких дощечек?
31.Сколько досок длиной 4 м, шириной 20 см и толщиной 30 мм выйдет
из бруса длиной 80 дм, имеющего в сечении прямоугольник размером
30 см × 40 см?33Найти площадь фигуры
34а)Две трубы, диаметры которых равны 7 см и 24 см, требуется заменить одной, площадь поперечного сечения которой равна сумме площадей поперечных сечений двух данных. Каким должен быть диаметр новой трубы? Ответ дайте в сантиметрах.
б)Две трубы, диаметры которых равны 36 см и 48 см, требуется заменить одной, площадь поперечного сечения которой равна сумме площадей поперечных сечений двух данных. Каким должен быть диаметр новой трубы? Ответ дайте в сантиметрах.
в)Две трубы, диаметры которых равны 63 см и 84 см, требуется заменить одной, площадь поперечного сечения которой равна сумме площадей поперечных сечений двух данных. Каким должен быть диаметр новой трубы? Ответ дайте в сантиметрах.
- 35.Найдите площадь квадрата, описанного вокруг окружности радиуса: а) 83Б)15
- б)Найдите площадь квадрата, если его диагональ равна 50
- б)Периметр квадрата равен 60. Найдите площадь квадрата
-
- в) Периметр ромба равен 32, а один из углов равен 30∘. Найдите площадь ромба.
- б) Периметр ромба равен 60, а один из углов равен 30∘. Найдите площадь ромба.
- 23.а) Периметр ромба равен 116, а один из углов равен 30∘. Найдите площадь ромба.
- д) Площадь ромба равна 48, а периметр равен 32. Найдите высоту ромба.
-
-
-
- б) Сторона ромба равна 18, а расстояние от центра ромба до неё равно 5. Найдите площадь ромба.
- 21.а) Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
- в)Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=7 и HD=24 Диагональ параллелограмма BD равна 51. Найдите площадь параллелограмма.
- б)Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=8 и HD=40. Диагональ параллелограмма BD равна 50. Найдите площадь параллелограмма.
-
-
-
- в)Основания равнобедренной трапеции равны 5 и 15, а её боковые стороны равны 13. Найдите площадь трапеции.
-
- б)Основания трапеции равны 6 и 20, одна из боковых сторон равна 13√2, а угол между ней и одним из оснований равен 135∘. Найдите площадь трапеции.
Андрей и его друзья собираются поехать в отпуск на две недели. Предварительно они наметили маршрут, представленный на рисунке. Они планируют на велосипедах добраться от города Гранюк до кемпинга, обозначенного на рисунке цифрой 7, за 4 дня, а потом поставить там палатки и отдыхать в море. Друзья собираются выехать рано утром и в первый день добраться до хутора Южный, где живёт бабушка Андрея. Там есть озеро, в котором можно купаться и ловить рыбу, что они и собираются делать до обеда следующего дня. Потом планируется доехать до посёлка Быково и заночевать там в мини‐отеле. На следующий день они собираются проехать 24 км до города Гусевск вдоль степного заказника и переночевать в одной из гостиниц. Заказник обозначен на рисунке цифрой 8. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Прямой путь короче, но там в эти дни идёт ремонт дороги, и пока неизвестно, где можно будет проехать быстрее.
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на рисунке. Заполните таблицу. В ответе запишите последовательность четырёх цифр без пробелов и других дополнительных символов.
| Объекты | Горд Гранюк | Деревня Астрелка |
Хутор Южный |
Город Гусевск |
| Цифры |
2. Ребята решили, что нужно взять в поездку чай в пакетиках определённого сорта. Оксане поручили купить чай на всех. Сколько пачек чая должна купить Оксана, если в компании 8 человек, в день они выпивают в среднем 3 пакетика на одного человека и поездка продлится две недели? В каждой пачке 25 пакетиков чая.
3. Найдите площадь (в км2), которую занимает заказник.
4. Все могут пойти в отпуск с 15 июля, кроме Григория и Марии, которым в этот день нужно работать. Они готовы выехать 16 июля и догнать остальную группу в посёлке Быково, не заезжая на хутор Южный. Найдите расстояние, которое проедут Григорий и Мария от города Гранюк до Быково. Ответ дайте в километрах.
5. Андрей выяснил, что его велосипед пришёл в нерабочее состояние. Андрей посетил сайты интернет‐магизина «ОК» и магазина «Вело», расположенного в соседнем доме, чтобы узнать некоторые цены. В этих магазинах можно купить готовый велосипед либо запасные части. Цены на продукцию магазинов и срок доставки из интернет‐ магазина даны в таблице.
| Продукция | Цена в магазине «Вело» (руб.) | Цена в магазине «ОК» (руб.) | Срок доставки из магазина «ОК» (дни) |
| Подсветка для спиц | 190 | 180 | 3 |
| Шина вида «А» | 680 | 650 | 12 |
| Шина вида «Б» | 1680 | 1450 | 12 |
| Спица | 70 | 80 | 3 |
| Педаль вида «А» | 437 | 405 | 10 |
| Педаль вида «Б» | 860 | 750 | 10 |
| Тормоз вида «А» | 1130 | нет | 10 |
| Тормоз вида «Б» | нет | 2180 | 10 |
| Набор крепёжных изделий | 740 | 765 | 14 |
Андрея не устраивает срок доставки деталей из интернет‐магазина, и он решил приобрести детали в магазине «Вело». Он готов потратить на ремонт не более 6000 рублей и при этом хочет купить самый дорогой набор для ремонта велосипеда, который может себе позволить. Ему нужно купить 5 спиц, 2 шины (одного вида), 2 педали (одного вида), тормоз (любого вида) и набор крепёжных изделий. Сколько рублей Андрей потратит на набор запасных частей?