С помощью данного калькулятора вы можете легко и быстро рассчитать площадь неправильного четырехугольника в условных единицах. Инструмент позволяет определить площадь выпуклой фигуры тремя разными способами: по сторонам, сторонам и углам, диагоналям и углам (первые два вычисления выполняются с ограничениями). Теоретическое обоснование расчета и формулы представлены ниже. Чтобы получить результат — выберите наиболее подходящий метод расчета, заполните поля калькулятора и нажмите кнопку «Рассчитать».
Как найти площадь неправильного четырехугольника?
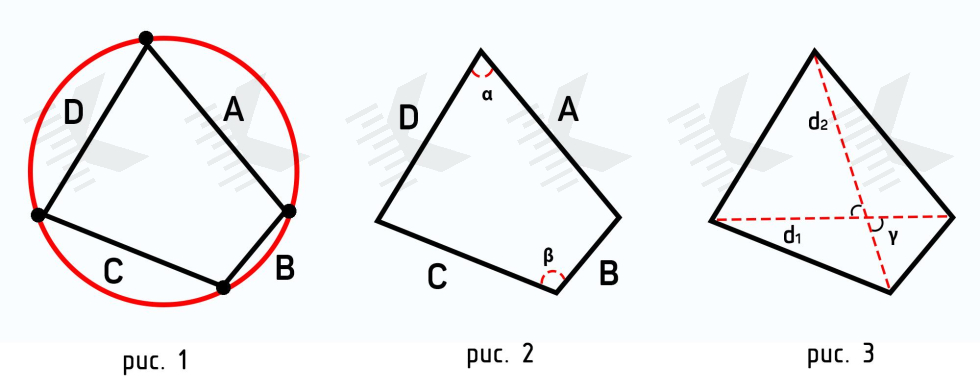
Первый способ расчета основан на формуле Брахмагупты (рис. 1), которая выражает площадь вписанного в окружность четырёхугольника как функцию длин его сторон. Эта формула является обобщением формулы Герона для площади треугольника.
![]()
где P — полупериметр, a, b, c, d — длины сторон четырехугольника.
Вторая формула также основывается на формуле Брахмагупты, но на ее расширенной версии (рис. 2), когда необходимо найти площадь произвольного четырехугольника.
![]()
где P — полупериметр, a, b, c, d — длины сторон, θ — полусумма противоположных углов четырёхугольника.
В формулах Брахмагупты есть одно ограничение — любая из сторон не может превышать полупериметр. В противном случае стороны четырехугольника не замкнутся. Математически, в формуле появится отрицательное значение.
Последняя формула позволяет найти площадь не самопересекающейся фигуры по проведенным диагоналям и синусу угла между ними (рис. 3). По сути, формула основывается на сумме площадей треугольников, которые образуются диагоналями четырехугольника.
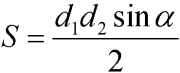
где d1, d2 — диагонали четырехугольника, α — острый угол между диагоналями.
Как рассчитать площадь четырехугольника
На данной странице калькулятор поможет рассчитать площадь четырехугольника онлайн. Для расчета задайте длину сторон, длины диагоналей и угол между ними, противолежащие углы, радиус окружности.
Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.
Через диагонали и угол между ними
Формула для нахождения площади четырехугольников через диагонали и угол между ними:
Через стороны и противолежащие углы
Формула для нахождения площади четырехугольников через стороны и противолежащие углы:
Площадь вписанного четырехугольника в окружность
Формула Брахмагупты для нахождения площади вписанного четырехугольника в окружность:
Площадь описанного четырехугольника около окружности через радиус
Формула для нахождения площади описанного четырехугольника около окружности через радиус:
Площадь неправильного четырехугольника
Узнайте чему равна площадь неправильного четырехугольника с помощью онлайн-калькулятора или по формулам — расчет по сторонам, диагоналям, углам.
С помощью данного калькулятора вы можете легко и быстро рассчитать площадь неправильного четырехугольника в условных единицах. Инструмент позволяет определить площадь выпуклой фигуры тремя разными способами: по сторонам, сторонам и углам, диагоналям и углам (первые два вычисления выполняются с ограничениями). Теоретическое обоснование расчета и формулы представлены ниже. Чтобы получить результат — выберите наиболее подходящий метод расчета, заполните поля калькулятора и нажмите кнопку «Рассчитать».
Как найти площадь неправильного четырехугольника?

Первый способ расчета основан на формуле Брахмагупты (рис. 1), которая выражает площадь вписанного в окружность четырёхугольника как функцию длин его сторон. Эта формула является обобщением формулы Герона для площади треугольника.

где P — полупериметр, a, b, c, d — длины сторон четырехугольника.
Вторая формула также основывается на формуле Брахмагупты, но на ее расширенной версии (рис. 2), когда необходимо найти площадь произвольного четырехугольника.

где P — полупериметр, a, b, c, d — длины сторон, θ — полусумма противоположных углов четырёхугольника.
В формулах Брахмагупты есть одно ограничение — любая из сторон не может превышать полупериметр. В противном случае стороны четырехугольника не замкнутся. Математически, в формуле появится отрицательное значение.
Последняя формула позволяет найти площадь не самопересекающейся фигуры по проведенным диагоналям и синусу угла между ними (рис. 3). По сути, формула основывается на сумме площадей треугольников, которые образуются диагоналями четырехугольника.

где d1, d2 — диагонали четырехугольника, α — острый угол между диагоналями .
Калькулятор расчета площади четырехугольника
В публикации представлены онлайн-калькуляторы и формулы для расчета площади выпуклого четырехугольника по разным исходным данным: через диагонали и угол между ними, по всем сторонам (если вокруг можно описать окружность), по полупериметру и радиусу вписанной окружности.
Расчет площади
Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь фигуры с учетом указанных данных.
1. Через диагонали и угол между ними
Формула расчета

2. По всем сторонам (формула Брахмагупты)
Примечание: Если вокруг четырехугольника можно описать окружность.
Формула расчета

p – полупериметр четырехугольника, равняется:
[spoiler title=”источники:”]
http://kalk.pro/math/area/ploshad-nepravilnogo-chetyrehugolnika/
[/spoiler]
Как рассчитать площадь четырехугольника
На данной странице калькулятор поможет рассчитать площадь четырехугольника онлайн. Для расчета задайте длину сторон, длины диагоналей и угол между ними, противолежащие углы, радиус окружности.
Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.
Через диагонали и угол между ними
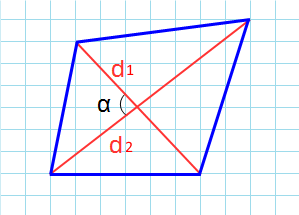
Формула для нахождения площади четырехугольников через диагонали и угол между ними:
d1, d2 – диагонали; α – угол между диагоналями.
Через стороны и противолежащие углы
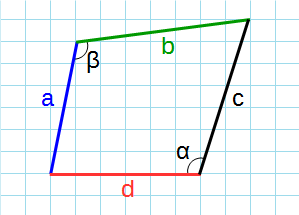
Формула для нахождения площади четырехугольников через стороны и противолежащие углы:
p – полупериметр четырехугольника; a, b, c, d – стороны четырехугольника; α, β – противолежащие углы.
Площадь вписанного четырехугольника в окружность
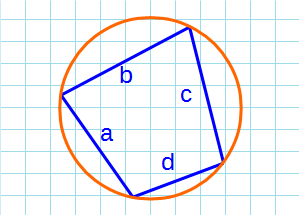
Формула Брахмагупты для нахождения площади вписанного четырехугольника в окружность:
p – полупериметр четырехугольника; a, b, c, d – стороны четырехугольника.
Площадь описанного четырехугольника около окружности через радиус
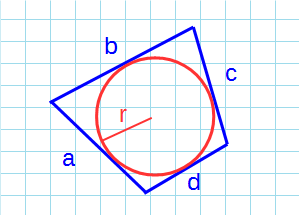
Формула для нахождения площади описанного четырехугольника около окружности через радиус:
p – полупериметр четырехугольника; r – радиус вписанной окружности; a, b, c, d – стороны четырехугольника.
Площадь описанного четырехугольника около окружности через стороны и противолежащие углы
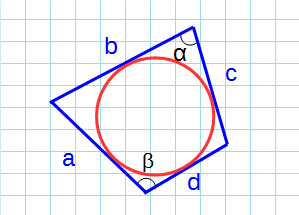
Формула для нахождения площади описанного четырехугольника около окружности через стороны и противолежащие углы:
p – полупериметр четырехугольника; a, b, c, d – стороны четырехугольника; α, β – противолежащие углы.
Ученик
(145),
закрыт
4 года назад
marat aminov
Просветленный
(32951)
4 года назад
пусть стороны четырехугольника а, b, c, d. если не заданы углы, то четырехугольник не жесткий и его площадь переменная. его площадь минимальна когда он вырождается в треугольник со сторонами а=250, f=(b+c)=333, d=102. в этом случае площадь находится по формуле Герона S(min)=√[p(p-a)(p-f)(p-d)], где p=(a+f+d)/2. S(min)=8507,5 ед^2. его площадь максимальна когда он вписывается в окружность (суммы противоположных углов равны 180 градусам). в этом случае площадь находится по формуле Брахмагупты S(max)=√[(p-a)(p-b)(p-c)(p-d), где p=(a+b+c+d)/2. S(max)=21754,57 ед^2.
Leonid
Высший разум
(388685)
4 года назад
Это невозможно.
Четырёхугольник – фигура нежёсткая, в отличие от треугольника. Это означает, что четырёхугольников с вот такими длинами сторон может быть сколько угодно. Просто представьте, что этот четырёхугольник собран из шарнирно соединённых реечек. Тогда если менять угол между двумя соседними реечками, две другие тоже будут как-то двигаться, а площадь фигуры будет при этом меняться.
Поэтому для вычисления площади, по фигу точного или приближённого, надо знать что-то ещё. Например, угол между двумя любыми соседними сторонами. Или координаты по крайней мере трёх вершин. Как-то так.
А в общем виде задача однозначного решения не имеет.
Константин Петров
Искусственный Интеллект
(150220)
4 года назад
для точного решения нужно знать либо размер диагоналей этого 4-угольника, либо значения углов
но…
есть такая крутая контора в ЕР под названием РОСРЕЕСТР https://pkk5.rosreestr.ru
ЭТА контора заявляется к владельцу земельного участка – типа мол плановая контрольная проверка
и в ходе этой проверки доказывает типа мол владелец захватил лишнюю землю, вымогая штраф
как вымогается штраф?
на основании чего?
а на том основании, что РОСРЕЕСТР обьявил нынешнюю математику неправильной, ошибочной
потому как правильная математика была лишь в древнем Вавилоне и древней Греции
используемая РОСРЕЕСТРом формула 0,5(a+c)*(b+d) ПО ЛЮБОМУ ВЫЯВЛЯЕТ излишки земли
обращение в суды РФ не помогают – суд выносит решения в пользу мошенников
так что, автору вопроса прямая дорога в РОСРЕЕСТР – ТАМ “точность” позволяет обогатиться
Рустам ИскендеровИскусственный Интеллект (133392)
4 года назад
В 90-е годы городской (городок в составе сельского района) муниципалитет выделил мне 56 соток земли. Общий участок имел вид трапеции высотой где-то километр или больше; известны были и основания этой большой трапеции. Мне и соседям (у каждого свой, в зависимости от числа членов семьи) участки были выделены проведением граничных линий параллельно указанным основаниям. Мой участок был где-то посередине. Не доверяя тамошним землемерам, сам проверил площадь. Всё совпало точь-в точь!.. Вот и вашему РОСРЕЕСТРУ проходить стажировку у землемеров нашего муниципалитета!..
Александр КузнецовУченик (145)
4 года назад
Костя, большое Вам спасибо за ответ. Это я решил вычислить площадь сельского кладбища, границы которого документально не определены. Могилы я уже все пересчитал и сфотографировал.
С уважением – А. Кузнецов
Рустам Искендеров
Искусственный Интеллект
(133392)
4 года назад
Минимальная площадь зависит и от последовательности расположения сторон, и от получаемой при “сжатии” четырёхугольника конфигурации. Пусть стороны 102 и 68 соседние. Если совместить их, налагая друг на друга, то получаем отрезок 102-68= 34 и, следовательно, 4-хугольник вырождается в некоторую фигуру, площадь которой определяет треугольник сторонами 34, 250 и 265. Формула Герона даёт минимальную площадь 3919,9, а не 8507,5, как указал М. Аминов в своём ответе.
Загрузить PDF
Загрузить PDF
Вам дана задача, в которой требуется найти площадь четырехугольника, а вы даже не знаете, что такое четырехугольник? Не волнуйтесь, эта статья вам поможет! Четырехугольник — это любая фигура с четырьмя сторонами. Для вычисления площади четырехугольника нужно определить тип четырехугольника, который вам дан, и воспользоваться соответствующей формулой.
-

1
Определение параллелограмма. Параллелограмм — это четырехугольник, у которого противоположные стороны равны и параллельны друг другу. Квадраты, прямоугольники и ромбы — это параллелограммы.
- Квадрат — это параллелограмм, у которого все стороны равны и пересекаются под прямым углом.
- Прямоугольник — это параллелограмм, у которого все стороны пересекаются под прямым углом.
- Ромб — это параллелограмм, у которого все стороны равны.
-

2
Площадь прямоугольника. Чтобы вычислить площадь прямоугольника, нужно знать его ширину (короткая сторона; представьте ее как высоту) и длину (длинная сторона; представьте ее как сторону, к которой проведена высота). Площадь прямоугольника равна произведению длины на ширину.
- ‘Площадь = длина х высота, или S = a х h.
- Пример: если длина прямоугольника равна 10 см, а ширина равна 5 см, то площадь этого прямоугольника: S = 10 х 5 = 50 квадратных сантиметров.
- Не забывайте, что площадь измеряется в квадратных единицах (квадратных метрах, квадратных сантиметрах и так далее).
-

3
Площадь квадрата. Квадрат — это частный случай прямоугольника, поэтому используйте ту же формулу, что и для нахождения площади прямоугольника. Но в квадрате все стороны равны, поэтому площадь квадрата равна любой из его сторон, возведенной в квадрат (то есть умноженной саму на себя).[1]
- Площадь = сторона х сторона, или S = a2.
- Пример: если сторона квадрата равна 4 см (a = 4), то площадь этого квадрата: S = a2 = 4 х 4 = 16 квадратных сантиметров.
-

4
Площадь ромба равна произведению его диагоналей, разделенной на два. Диагонали — это отрезки, соединяющие противоположные вершины ромба.[2]
- Площадь = (диагональ1 х диагональ2)/2, или S = (d1 × d2)/2
- Пример: если диагонали ромба равны 6 см и 8 см, то площадь этого ромба: S = (6 х 8)/2 = 24 квадратных сантиметров.
-

5
Площадь ромба также можно найти, если умножить его сторону на высоту, опущенную на эту сторону. Но не путайте высоту со смежной стороной. Высота — это прямая, опущенная из любой вершины ромба на противоположную сторону, и пересекающая противоположную сторону под прямым углом.
- Пример: если длина ромба равна 10 см, а его высота равна 3 см, то площадь такого ромба равна 10 х 3 = 30 квадратных сантиметров.
-

6
Формулы для вычисления площадей ромба и прямоугольника применимы к квадратам, так как квадрат — это частный случай как прямоугольника, так и ромба.
- Площадь = сторона х высоту, или S = a × h
- Площадь = (диагональ1 × диагональ2)/2, или S = (d1 × d2)/2
- Пример: если сторона квадрата равна 4 см, то его площадь равна 4 х 4 = 16 квадратных сантиметров.
- Пример: диагонали квадрата равны по 10 см. Вы можете найти площадь этого квадрата по формуле: (10 х 10)/2 = 100/2 = 50 квадратных сантиметров.
Реклама
-

1
Определение трапеции. Трапеция — это четырехугольник, у которого две противоположные стороны параллельны друг другу. Каждая из четырех сторон трапеции может быть разной длины.
- Есть два способа вычисления площади трапеции (в зависимости от данных значений).
-

2
Найдите высоту трапеции. Высота трапеции — отрезок, соединяющий параллельные стороны (основания) и пересекающий их под прямым углом (высота не равна боковым сторонам). Вот как найти высоту трапеции:[3]
- Из точки пересечения меньшего основания и боковой стороны проведите перпендикуляр к большему основанию. Этот перпендикуляр и есть высота трапеции.
- Чтобы вычислить высоту, используйте тригонометрию. Например, если вы знаете боковую сторону и прилегающий к ней угол, то высота равна произведению боковой стороны на синус прилегающего угла.
-

3
Найдите площадь трапеции, используя высоту. Если вы знаете высоту трапеции и оба основания, используйте следующую формулу для вычисления площади трапеции:
- Площадь = (основание1 + основание2)/2 × высота, или S = (a+b)/2 × h
- Пример: если высота трапеции равна 2 см, а основания трапеции равны 7 см и 11 см, то площадь этой трапеции: S = (a+b)/2 * h = (7 + 11)/2 * 2 = 18 квадратных сантиметров.
- Если высота трапеции равна 10, а основания трапеции равны 7 и 9, то площадь этой трапеции: S = (a+b)/2 * h = (7 + 9)/2 * 10 = (16/2) * 10 = 8 * 10 = 80.
-

4
Найдите площадь трапеции, используя среднюю линию. Средняя линия — это отрезок, параллельный основаниям и делящий боковые стороны пополам. Средняя линия равна среднему значению от обоих оснований (a и b): средняя линия = (a+b)/2.
- Площадь = средняя линия х высота, или S = m × h
- По сути, здесь вы используете формулу для нахождения площади трапеции по двум основаниям, но вместо (a+b)/2 подставлена m (средняя линия).
- Пример: если средняя линия трапеции равна 9 см, то площадь этой трапеции: S = m*h = 9 х 2 = 18 квадратных сантиметров (вы получили тот же ответ, что и в предыдущем шаге).
Реклама
-

1
Определение дельтоида. Дельтоид — это четырехугольник с двумя парами сторон одинаковой длины.
- Есть два способа вычисления площади дельтоида (в зависимости от данных значений).
-

2
Найдите площадь дельтоида, используя формулу для нахождения площади ромба (с использованием диагоналей), так как ромб — это частный случай дельтоида, у которого все стороны равны. Напомним, что диагональ — отрезок, соединяющий противоположные вершины.
- Площадь = (диагональ1 х диагональ2)/2, или S = (d1 × d2)/2
- Пример: если диагонали дельтоида равны 19 см и 5 см, то площадь этого дельтоида: S = (19 х 5)/2 = 47,5 квадратных сантиметров.
- Если вы не знаете длины диагоналей и не можете их измерить, используйте тригонометрию, чтобы вычислить их. Прочтите эту статью, чтобы узнать больше информации.
-

3
Найдите площадь дельтоида, используя неравные стороны и угол между ними. Если вы знаете неравные стороны и угол между этими сторонами (θ), то площадь дельтоида вычисляется с помощью тригонометрии по формуле:[4]
- Площадь = (сторона1 х сторона2) х sin (угол), или S = (a × b) × sin(θ), где θ — угол между неравными сторонами.
- Пример: Если стороны дельтоида равны 4 см и 6 см, а угол между ними равен 120 градусам, то площадь дельтоида равна (6 х 4) х sin120 = 24 х 0,866 = 20,78 квадратных сантиметров.
- Обратите внимание, что вы должны использовать две неравные стороны и угол между ними; если вы используете две равные стороны и угол между ними, вы получите неправильный ответ.
Реклама
-

1
Если вам дан четырехугольник произвольной формы, то даже для таких четырехугольников существуют формулы для вычисления их площадей. Обратите внимание, что такие формулы требуют знания тригонометрии.
- Во-первых, найдите длины всех четырех сторон. Обозначим их через a, b, c, d (а напротив с, а b напротив d).
- Пример: дан четырехугольник произвольной формы со сторонами 12 см, 9 см, 5 см и 14 см.
-

2
Найдите угол А между сторонами а и d и угол С между сторонами b и с (вы можете найти любые два противолежащих угла).
- Пример: в нашем четырехугольнике А = 80 градусов и C = 110 градусов.
-

3
Представьте, что существует отрезок, соединяющий вершины, образованные сторонами а и b и сторонами с и d. Этот отрезок разделит четырехугольник на два треугольника. Так как площадь треугольника равна 1/2absinC, где C — угол между сторонами a и b, вы можете найти площади двух треугольников и сложить их, чтобы вычислить площадь квадрата.
- Площадь = 0,5 х сторона1 х сторона4 х sin(угол между стороной1 и стороной4) + 0,5 х сторона2 х сторона3 х sin(угол между стороной2 и стороной3), или
- Площадь = 0,5 a × d × sin A + 0,5 × b × c × sin C
-
Пример: вы нашли стороны и углы, поэтому просто подставьте их в формулу.
-
- = 0,5 (12 × 14) × sin (80) + 0,5 × (9 × 5) × sin (110)
- = 84 × sin (80) + 22,5 × sin (110)
- = 84 × 0,984 + 22,5 × 0,939
- = 82,66 + 21,13 = 103,79 квадратных сантиметров.
-
- Обратите внимание, что если вы пытаетесь найти площадь параллелограмма (у которого противоположные углы равны), то формула примет вид: площадь = 0.5*(ad + bc) * sin A
Реклама
Советы
-
Этот калькулятор для вычисления площади треугольника пригодится вам при вычислении площади четырехугольника произвольной формы.[5]
- Чтобы получить дополнительную информацию, прочитайте статьи по вычислению площади квадрата, площади прямоугольника, площади ромба, площади трапеции и площади дельтоида.
Реклама
Об этой статье
Эту страницу просматривали 440 328 раз.
