Определенный интеграл. Площадь криволинейной трапеции
- Теорема о площади криволинейной трапеции
- Формула Ньютона-Лейбница
- Геометрический смысл теоремы Лагранжа о среднем
- Площадь плоской фигуры, ограниченной двумя кривыми
- Примеры
п.1. Теорема о площади криволинейной трапеции
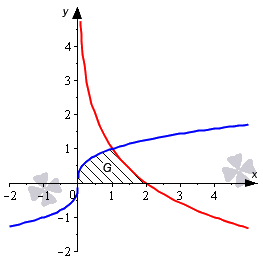
Фигуру, ограниченную прямыми (x=a, x=b), осью абсцисс (y=0) и графиком функции (y=f(x)) называют криволинейной трапецией.
Теорема
Площадь криволинейной трапеции, образованной графиком функции (y=f(x)) на интервале [a;b], равна (F(b)-F(a)), где (F(x)) – первообразная функции (f(x)) на [a;b].
Доказательство:
Выберем на интервале (xin [a;b]). Площадь соответствующей криволинейной трапеции (S(x)) является функцией от (x). Дадим переменной (x) приращение (triangle x).
Площадь криволинейной трапеции на интервале (left[a;x+triangle xright]) равна сумме
(S(x+triangle x)=S(x)+S(triangle x)). Откуда приращение площади: $$ triangle S=S(triangle x)=S(x+triangle x)-S(x) $$ По теореме о среднем (см. ниже в этом параграфе) между (x) и (x+triangle x) всегда найдется такое (t), что приращение площади равно произведению: $$ triangle S=f(t)cdot (x+triangle x-x)=f(t)cdot triangle x $$ Если (triangle xrightarrow 0), то (trightarrow x), и в пределе получаем: begin{gather*} S'(x)=lim_{triangle xrightarrow 0}frac{triangle S}{triangle x}=lim_{triangle xrightarrow 0} frac{f(t)cdot triangle x}{triangle x}=lim_{triangle xrightarrow 0}f(t)=f(x) end{gather*} Т.е. (S(x)) является первообразной для (f(x)) на [a;b]. В общем виде: $$ S(x)=F(x)+C $$ Найдем C. В точке a: $$ S(a)=0=F(a)+CRightarrow C=-F(a) $$ Тогда вся площадь: $$ S=S(b)=F(b)+C=F(b)-F(a) $$ Что и требовалось доказать.
п.2. Формула Ньютона-Лейбница
Площадь криволинейной трапеции, образованной графиком функции (y=f(x)) на интервале [a;b] записывают в виде определенного интеграла: $$ S=int_{a}^{b}f(x)dx $$ По формуле Ньютона-Лейбница определенный интеграл равен: $$ int_{a}^{b}f(x)dx=F(x)|_a^b=F(a)-F(b) $$
Например:
Найдем площадь фигуры, ограниченной осью абсцисс и графиком функции $$ y=3-2x-x^2 $$
 |
Построим график (см. §28 справочника для 8 класса). Это парабола. (alt 0) – ветки вниз. Координаты вершины: begin{gather*} x_0=-frac{b}{2a}=-frac{-2}{2cdot (-1)}=-1,\ y_0=3+2-1=4 end{gather*} Точки пересечения с осью OX: begin{gather*} 3-2x-x^2=0Rightarrow x^2+2x-3=0\ (x+3)(x-1)=0Rightarrow left[ begin{array}{l} x=-3,\ x=1 end{array} right. end{gather*} Точка пересечения с осью OY: $$ x=0, y=3 $$ |
Необходимо найти площадь заштрихованной фигуры.
Функция: (f(x)=3-2x-x^2)
Пределы интегрирования: (a=-3, b=1) begin{gather*} S=int_{-3}^{1}(3-2x-x^2)dx=left(3x-2cdotfrac{x^2}{2}-frac{x^3}{3}right)|_{1}^{-3}=left(3x-x^2-frac{x^3}{3}right)|_{1}^{-3}=\ =left(3-cdot 1-1^2-frac{1^3}{3}right)-left(3cdot(-3)-(-3)^2-frac{(-3)^3}{3}right)=2-frac13+9=10frac23 end{gather*} Ответ: (10frac23)
п.3. Геометрический смысл теоремы Лагранжа о среднем
Теорема Лагранжа о среднем
Если функция (F(x)) непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), то существует такая точка (muin(a;b)), что $$ F(b)-F(a)=F'(mu)(a-b) $$ Пусть (F'(x)=f(x)), т.е. функция (F(x)) является первообразной для (f(x)). Тогда: $$ F(b)-F(a)=int_{a}^{b}f(x)dx=f(mu)(b-a) $$
Геометрический смысл теоремы Лагранжа о среднем в интегральной форме заключается в том, что площадь криволинейной трапеции равна площади прямоугольника с основанием (d=b-a) и высотой (h=f(mu)), где (aleqmuleq b).
Теорема о среднем используется при доказательстве многих формул, связанных с использованием определенных интегралов (центра тяжести тела, площади поверхности и т.д.).
п.4. Площадь плоской фигуры, ограниченной двумя кривыми
Площадь плоской фигуры, ограниченной прямыми (x=a, x=b, alt b) и кривыми (y=f(x), y=g(x)), причем (f(x)geq g(x)) для любого (xin [a;b]), равна: $$ S=int_{a}^{b}(f(x)-g(x))dx $$
Например:
Найдем площадь фигуры, ограниченной двумя параболами (y=x^2) и (y=4x-x^2).
Найдем точки пересечения парабол: $$ x^2=4x-x^2Rightarrow 2x^2-4x=0Rightarrow 2x(x-2)=0Rightarrow left[ begin{array}{l} x=0\ x=2 end{array} right. $$ Строим графики.
Необходимо найти площадь заштрихованной фигуры.
Функция сверху: (f(x)=4x-x^2)
Функция снизу: (g(x)=x^2)
Пределы интегрирования: (a=0, b=2) begin{gather*} S=int_{0}^{2}left((4x-x^2)-x^2right)dx=int_{0}^{2}(4x-2x^2)dx=left(4cdotfrac{x^2}{2}-2cdotfrac{x^3}{3}right)|_0^2=\ =left(2x^2-frac23 x^3right)|_0^2=2cdot 2^2-frac23cdot 2^3-0=8-frac{16}{3}=frac83=2frac23 end{gather*} Ответ: (2frac23)
п.5. Примеры
Пример 1. Найдите определенный интеграл:
a) (int_{-2}^{3}x^2dx) $$ int_{-2}^{3}x^2dx=frac{x^3}{3}|_{-2}^{3}=frac{3^3}{3}-frac{(-2)^3}{3}=9-frac83=frac{19}{3}=6frac13 $$
б) (int_{0}^{fracpi 3}sinxdx) $$ int_{0}^{fracpi 3}sinxdx=(-cosx)|_{0}^{fracpi 3}=-cosfracpi 3+cos0=-frac12+1=frac12 $$
в) (int_{1}^{2}left(e^x+frac 1xright)dx) $$ int_{1}^{2}left(e^x+frac 1xright)dx=(e^x+ln|x|)|_{1}^{2}=e^2+ln 2-e^1-underbrace{ln 1}_{=0}=e(e-1)+ln 2 $$
г) (int_{2}^{3}(2x-1)^2 dx) begin{gather*} int_{2}^{3}(2x-1)^2 dx=frac12cdotfrac{(2x-3)^3}{3}|_{2}^{3}=frac16((2cdot 3-1)^3)-(2cdot 2-1)^3)=frac{5^3-3^3}{6}=\ =frac{125-27}{6}=frac{98}{6}=frac{49}{3}=16frac13 end{gather*}
д) (int_{1}^{3}frac{dx}{3x-2}) begin{gather*} int_{1}^{3}frac{dx}{3x-2}=frac13cdot ln|3x-2| |_{1}^{3}=frac13left(ln 7-underbrace{ln 1}_{=0}right)=frac{ln 7}{3} end{gather*}
e) (int_{-1}^{4}frac{dx}{sqrt{3x+4}}) begin{gather*} int_{-1}^{4}frac{dx}{sqrt{3x+4}}=frac13cdotfrac{(3x+4)^{-frac12+1}}{-frac12+1}|_{-1}^{4}=frac23sqrt{3x+4}|_{-1}^{4}=\ =frac23left(sqrt{3cdot 4+4}-sqrt{3cdot(-1)+4}right)=frac23(4-1)=2 end{gather*}
Пример 2. Найдите площадь фигуры под кривой на заданном интервале:
a) (f(x)=x^3+3, xinleft[-1;1right])
б) (f(x)=sin2x, xinleft[0;fracpi 2right])
в) (f(x)=frac4x+3, xinleft[2;6right])
(f(x)=frac4x+3) – гипербола с асимптотами (x=0, y=3)
Площадь под кривой: begin{gather*} S=int_{2}^{6}left(frac4x+3right)dx=(4cdot ln|x|+3x)|_{2}^{6}=(4ln 6+18)-(4ln 2+6)=\ =4(ln 6-ln 2)+12=4lnfrac62+12=4ln 3+12=4(ln 3+3) end{gather*}
г) (f(x)=frac{1}{sqrt{x}}, xinleft[1;4right])
Пример 3. Найдите площадь фигуры, ограниченной линиями:
a) (y=x-2, y=x^2-4x+2)
Найдем точки пересечения прямой и параболы: $$ x-2=x^2-4x+2Rightarrow x^2-5x+4=0Rightarrow (x-1)(x-4)=0Rightarrow left[ begin{array}{l} x=1,\ x=4 end{array} right. $$
Функция сверху: (f(x)=x-2)
Функция снизу: (g(x)=x^2-4x+2)
Пределы интегрирования: (a=1, b=4) begin{gather*} S=int_{1}^{4}left((x-2)-(x^2-4x+2)right)dx=int_{1}^{4}(-x^2+5x-4)dx=\ =left(-frac{x^3}{3}+frac{5x^2}{2}-4xright)|_{1}^{4}=left(-frac{64}{3}+5cdotfrac{16}{2}-4cdot 4right)-left(-frac13+frac52-4right)=\ =-frac{63}{3}+24+1,5=4,5 end{gather*} Ответ: 4,5
б) (y=e^{frac x2}, y=frac1x, x=2, x=3)
Функция сверху: (f(x)=e^{x/2})
Функция снизу: (g(x)=frac1x)
Пределы интегрирования: (a=2, b=3) begin{gather*} S=int_{2}^{3}left(e^{x/2}-frac1xright)dx=(2e^{x/2}-ln|x|)|_{2}^{3}=left(2e^{frac32}-ln 3right)-(2e-ln 2)=\ =2e^{frac32}-2e-ln 3+ln 2=2e(sqrt{e}-1)+lnfrac23 end{gather*} Ответ: (2e(sqrt{e}-1)+lnfrac23)
в*) (y=3-x^2, y=1+|x|)
Найдем точки пересечения ломаной и параболы: begin{gather*} 3-x^2=1+|x|Rightarrow x^2+|x|-2=0Rightarrow left[ begin{array}{l} begin{cases} xgeq 0\ x^2+x-2=0 end{cases} \ begin{cases} xlt 0\ x^2-x-2=0 end{cases} end{array} right. Rightarrow left[ begin{array}{l} begin{cases} xgeq 0\ (x+2)(x-1)=0 end{cases} \ begin{cases} xlt 0\ (x-2)(x+1)=0 end{cases} end{array} right. Rightarrow \ left[ begin{array}{l} begin{cases} xgeq 0\ left[ begin{array}{l} x=-2\ x=1 end{array} right. end{cases} \ begin{cases} xlt 0\ left[ begin{array}{l} x=2\ x=-1 end{array} right. end{cases} end{array} right. Rightarrow left[ begin{array}{l} x=1\ x=-1 end{array} right. end{gather*}
Функция сверху: (f(x)=3-x^2)
Функция снизу: (g(x)=1+|x|)
Пределы интегрирования: (a=-1, b=1)
Чтобы не раскрывать модуль под интегралом, заметим, что площади на интервалах [-1;0] и [0;1] равны, т.к. обе функции четные и симметричные относительно оси OY. Поэтому можно рассматривать только положительные (xinleft[0;1right]), найти для них интеграл (площадь) и умножить на 2: begin{gather*} S=2int_{0}^{1}left((3-x^2)-(1+x)right)dx=2int_{0}^{1}(-x^2-x+2)dx=2left(-frac{x^3}{3}-frac{x^2}{2}+2xright)|_{0}^{1}=\ =2left(-frac13-frac12+2right)-0=frac73=2frac13 end{gather*} Ответ: (2frac13)
г*) (y=3sinx, y=cosx, x=-frac{5pi}{4}, x=fracpi 4)
На отрезке (left[-frac{5pi}{4};-frac{3pi}{4}right]) синус над косинусом, далее на (left[-frac{3pi}{4};frac{pi}{4}right]) – косинус над синусом.
Площадь фигуры, закрашенной голубым, в два раза больше площади фигуры, закрашенной сиреневым. Поэтому общая площадь будет равна трем площадям, закрашенным сиреневым: begin{gather*} S=3int_{-frac{5pi}{4}}^{-frac{3pi}{4}}(sinx-cosx)dx=3(-cosx-sinx)|_{-frac{5pi}{4}}^{-frac{3pi}{4}}=-3(cosx+sinx)|_{-frac{5pi}{4}}^{-frac{3pi}{4}} end{gather*} Прибавим полный период, он одинаков для обеих функций:
(-frac{3pi}{4}+2pi=frac{5pi}{4}; -frac{5pi}{4}+2pi=frac{3pi}{4}) begin{gather*} -3(cosx+sinx)|_{-frac{5pi}{4}}^{-frac{3pi}{4}}=-3left(cosleft(frac{5pi}{4}right)+sinleft(frac{5pi}{4}right)-cosleft(frac{3pi}{4}right)-sinleft(frac{3pi}{4}right)right)=\ =-3left(-frac{sqrt{2}}{2}-frac{sqrt{2}}{2}+frac{sqrt{2}}{2}-frac{sqrt{2}}{2}right)=3sqrt{2} end{gather*} Ответ: (3sqrt{2})
Пример 4*. Пусть (S(k)) – это площадь фигуры, образованной параболой (y=x^2+2x-3) и прямой (y=kx+1). Найдите (S(-1)) и вычислите наименьшее значение (S(k)).
1) Найдем (S(-1)).
(k=-1, y=-x+1 )
 |
Точки пересечения прямой и параболы: begin{gather*} -x+1=x^2+2x-3\ x^2+3x-4=0\ (x+4)(x-1)=0Rightarrow left[ begin{array}{l} x=-4,\ x=1 end{array} right. end{gather*} Функция сверху: (y=-x+1) Функция снизу: (y=x^2+2x-3) Пределы интегрирования: (a=-4, b=1) |
begin{gather*} S(-1)=int_{-4}^{1}left((-x+1)-(x^2+2x-3)right)dx=int_{-4}^{1}(-x-3x+4)dx=\ =left(-frac{x^3}{3}-frac{3x^2}{2}+4xright)|_{-4}^{1}=left(-frac13-frac32+4right)-left(frac{64}{3}-24-16right)=-21frac23+42frac12=20frac56 end{gather*}
2) Решаем в общем виде.
Все прямые (y=kx+1) проходят через точку (0;1) и при образовании фигуры находятся над параболой.
Точки пересечения прямой и параболы: begin{gather*} kx+1=x^2+2x-3Rightarrow x^2+(2-k)x-4=0\ D=(2-k)^2-4cdot (-4)=(k-2)^2+16gt 0 end{gather*} Дискриминант (Dgt 0) при всех (k). Точки пересечения (пределы интегрирования): $$ x_{1,2}=frac{-(2-k)pmsqrt{D}}{2}=frac{k-2pmsqrt{D}}{2} $$ Разность корней: $$ x_2-x_1=sqrt{D}=sqrt{(k-2)^2+16} $$ Минимальное значение разности корней будет при (k=2).
Площадь: begin{gather*} S(k)=int_{x_1}^{x_2}left((kx+1)-(x^2+2x-3)right)dx=int_{x_1}^{x_2}(-x^2+(k-2)x+4)dx=\ =left(-frac{x^3}{3}+frac{(k-2)x^2}{2}+4xright)|_{x_1}^{x_2}=-frac13(x_2^3-x_1^3)+frac{k-2}{2}(x_2^2-x_1^2)+4(x_2-x_1) end{gather*}
 |
begin{gather*} S(k)_{min}=S(2)\ x_{1,2}=pm 2\ S(2)=-frac13cdot(2^3+2^3)+0+4sqrt{16}=\ =-frac{16}{3}+16=frac{32}{3}=10frac23 end{gather*} |
Ответ: 1) (S(-1)=20frac56); 2) (S(k)_{min}=S(2)=10frac23)
Пример 5*. Фигура ограничена линиями (y=(x+3)^2, y=0, x=0). Под каким углом к оси OX надо провести прямые через точку (0;9), чтобы они разбивали фигуру на три равновеликие части?
 |
Площадь криволинейной трапеции AOB: begin{gather*} S_0=int_{-3}^{0}(x+3)^2dx=frac{(x+3)^3}{3}|_{-3}^{0}=\ =9-0=9 end{gather*} Площадь каждой части: (S_i=frac13 S_0=3) Точки (C(x_1; 0)) и (D(x_2; 0)) c (-3lt x_1lt x_2lt 0) такие, что прямые AC и AD отсекают по 1/3 от фигуры. Площадь прямоугольного треугольника (triangle AOD): begin{gather*} S_3=frac12|x_2|cdot 9=3Rightarrow |x_2|=frac69=frac23Rightarrow\ x_2=-frac23 end{gather*} Площадь прямоугольного треугольника (triangle AOC): begin{gather*} S_2+S_3=frac12|x_1|cdot 9=6Rightarrow |x_1|=frac{12}{9}=frac43Rightarrow\ x_1=-frac43 end{gather*} |
Находим углы соответствующих прямых.
Для (x_1: tgalpha=frac{9}{|x_1|}=frac{9}{4/3}=frac{27}{4}, alpha=arctgfrac{27}{4})
Для (x_x: tgbeta=frac{9}{|x_2|}=frac{9}{2/3}=frac{27}{2}, beta=arctgfrac{27}{2})
Ответ: (arctgfrac{27}{4}) и (arctgfrac{27}{2})
На чтение 2 мин. Просмотров 43k.
Площадь криволинейной трапеции, ограниченной сверху графиком функции y=f (x), снизу — осью Ох, слева и справа прямыми х=a, x=b, находят по формуле Ньютона-Лейбница (ф. Н-Л):
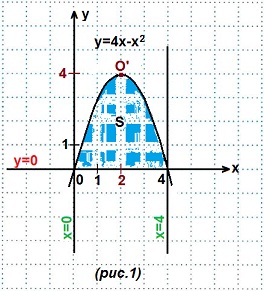
Решение. Строим графики данных линий. (рис. 1).
1) y=4x-x² — парабола (вида y=ax²+bx+c). Запишем данное уравнение в общем виде: y=-x²+4x. Ветви этой параболы направлены вниз, так как первый коэффициент а=-1<0.
Вершина параболы находится
в точке O′(m; n), где
О′(2; 4). Нули функции (точки пересечения графика с осью Ох) найдем из уравнения:
4х-х²=0.
Выносим х за скобки, получаем: х(4-х)=0. Отсюда, х=0 или х=4. Абсциссы точек найдены, ордината равна нулю — искомые точки: (0; 0) и (4; 0).
2) y=0 — это ось Ох; 3) х=0 — это ось Оy; 4) х=4 — прямая, параллельная оси Оy и отстоящая от нее на 4 единичных отрезка вправо.
Площадь построенной криволинейной трапеции находим по (ф. Н-Л). У нас f (x)=4x-x², a=0, b=4.
Кстати, если Вы подсчитаете все целые заштрихованные клетки и добавите к ним половину всех остальных клеток заштрихованной фигуры, то получите приближенное значение искомой площади. Действительно, если единичный отрезок равен одной клетке, то площадь квадратика со стороной, равной 1 клетке, равна 1·1=1 (кв. ед.). Сколько квадратиков — столько квадратных единиц и составляет площадь фигуры.
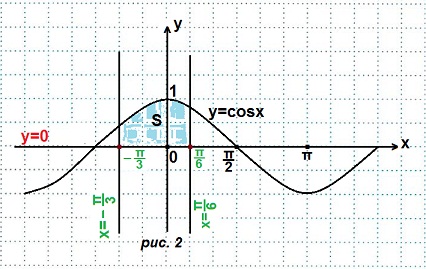
Пример 2. Найти площадь криволинейной трапеции, ограниченной линиями:
Решение. Строим графики данных линий. (рис. 2).
Площадь данной криволинейной трапеции:
( 11 оценок, среднее 3.55 из 5 )
Содержание:
- Примеры с решением
Рассмотрим функцию 





На рисунке 26.1 приведены примеры криволинейных трапеций.
Рассмотрим теорему, которая позволяет вычислять площади криволинейных трапеций.
Теорема 26.1.
Площадь 





где 


По этой ссылке вы найдёте полный курс лекций по высшей математике:
Доказательство. Рассмотрим функцию 

Если 



Докажем, что 

Пусть 





Имеем:
Получаем, что 
На отрезке 






Если 

Возможно вам будут полезны данные страницы:
Поскольку функция 




Имеем
Поскольку 






Пусть 


где 
Имеем:
По определению функции 


Примеры с решением
Пример 1.
Найдите площадь 



Решение:
На рисунке 26.5 изображена криволинейная трапеция, площадь которой требуется найти.
Одной из первообразных функции 


Пример 2.
Найдите площадь 


Решение:
График функции 





Одной из первообразных функции 


Определение. Пусть
— первообразная функции
на промежутке
, числа
и
, где
, принадлежат промежутку
. Разность
называют определенным интегралом функции
на отрезке
.
Определенный интеграл функции 





где 


Например, функция 





Заметим, что значение разности 






Равенство (1) называют формулой Ньютона—Лейбница. Следовательно, для вычисления определенного интеграла 
- найти любую первообразную
функции
на отрезке
;
- вычислить значение первообразной
в точках
и
;
- найти разность
.
При вычислении определенных интегралов разность 
Используя такое обозначение, вычислим, например, 
Пример 3.
Вычислите
Решение:
Имеем:
Если функция 



Действительно,
Если каждая из функций 


-
где
— некоторое число.
Формула Ньютона-Лейбница позволяет установить связь между определенным интегралом и площадью 





Используя теорему 26.1, можно записать:
Заметим, что в этой формуле рассматриваются непрерывные функции 

Рассмотрим непрерывные на отрезке 



Покажем, как найти площадь
фигуры
, ограниченной графиками функций
и
и прямыми
и
(рис. 26.7).
Перенесем фигуру 







Поскольку фигуры 


где 









Таким образом, используя свойства определенного интеграла, можем записать:
Следовательно, если функции 









Пример 4.
Найдите площадь 

Решение:
На рисунке 26.10 изображена фигура, площадь которой требуется найти.
Решив уравнение 




Тогда искомая площадь
Лекции:
- Экспонента, натуральные логарифмы и гиперболические функции
- Непрерывная случайная величина
- Математическое ожидание и дисперсия случайной величины
- Исследование функции: пример решения
- Понятие функции. Теория пределов
- Элементарные функции комплексного переменного. Дробно-рациональные функции
- Равномерная сходимость функционального ряда
- Критерий Сильвестра
- Преобразования в пространстве и на плоскости
- Площадь поверхности подобных фигур
В предыдущем разделе, посвященном разбору геометрического смысла определенного интеграла, мы получили ряд формул для вычисления площади криволинейной трапеции:
S(G)=∫abf(x)dx для непрерывной и неотрицательной функции y=f(x) на отрезке [a;b],
S(G)=-∫abf(x)dx для непрерывной и неположительной функции y=f(x) на отрезке [a;b].
Эти формулы применимы для решения относительно простых задач. На деле же нам чаще придется работать с более сложными фигурами. В связи с этим, данный раздел мы посвятим разбору алгоритмов вычисления площади фигур, которые ограничены функциями в явном виде, т.е. как y=f(x) или x=g(y).
Формула для вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y)
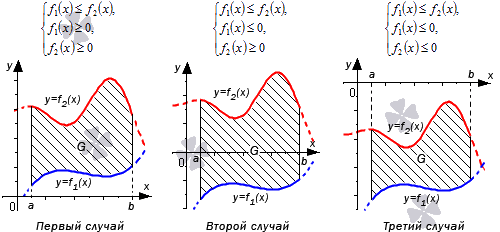
Пусть функции y=f1(x) и y=f2(x) определены и непрерывны на отрезке [a;b], причем f1(x)≤f2(x) для любого значения x из [a;b]. Тогда формула для вычисления площади фигуры G, ограниченной линиями x=a, x=b, y=f1(x) и y=f2(x) будет иметь вид S(G)=∫abf2(x)-f1(x)dx.
Похожая формула будет применима для площади фигуры, ограниченной линиями y=c, y=d, x=g1(y) и x=g2(y): S(G)=∫cd(g2(y)-g1(y)dy.
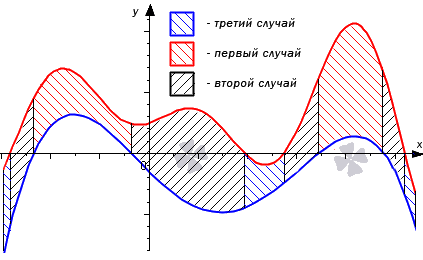
Разберем три случая, для которых формула будет справедлива.
В первом случае, учитывая свойство аддитивности площади, сумма площадей исходной фигуры G и криволинейной трапеции G1 равна площади фигуры G2. Это значит, что
Поэтому, S(G)=S(G2)-S(G1)=∫abf2(x)dx-∫abf1(x)dx=∫ab(f2(x)-f1(x))dx.
Выполнить последний переход мы можем с использованием третьего свойства определенного интеграла.
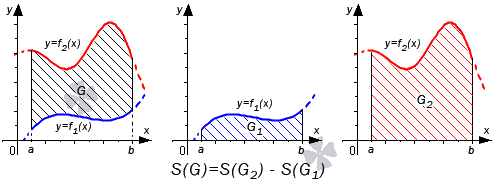
Во втором случае справедливо равенство: S(G)=S(G2)+S(G1)=∫abf2(x)dx+-∫abf1(x)dx=∫ab(f2(x)-f1(x))dx
Графическая иллюстрация будет иметь вид:
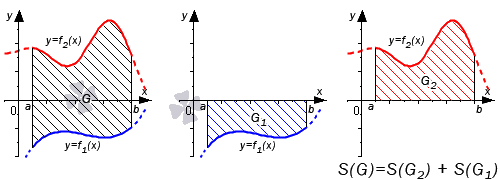
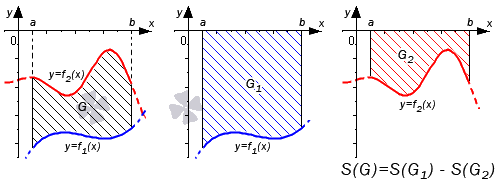
Если обе функции неположительные, получаем: S(G)=S(G2)-S(G1)=-∫abf2(x)dx–∫abf1(x)dx=∫ab(f2(x)-f1(x))dx . Графическая иллюстрация будет иметь вид:
Перейдем к рассмотрению общего случая, когда y=f1(x) и y=f2(x) пересекают ось Ox.
Точки пересечения мы обозначим как xi, i=1, 2,…, n-1. Эти точки разбивают отрезок [a; b] на n частей xi-1; xi, i=1, 2,…, n, где α=x0<x1<x2<…<xn-1<xn=b. Фигуру G можно представить объединением фигур Gi, i=1, 2,…, n. Очевидно, что на своем интервале Gi попадает под один из трех рассмотренных ранее случаев, поэтому их площади находятся как S(Gi)=∫xi-1xi(f2(x)-f1(x))dx, i=1, 2,…, n
Следовательно,
S(G)=∑i=1nS(Gi)=∑i=1n∫xixif2(x)-f1(x))dx==∫x0xn(f2(x)-f(x))dx=∫abf2(x)-f1(x)dx
Последний переход мы можем осуществить с использованием пятого свойства определенного интеграла.
Проиллюстрируем на графике общий случай.
Формулу S(G)=∫abf2(x)-f1(x)dx можно считать доказанной.
А теперь перейдем к разбору примеров вычисления площади фигур, которые ограничены линиями y=f(x) и x=g(y).
Примеры вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y)
Рассмотрение любого из примеров мы будем начинать с построения графика. Изображение позволит нам представлять сложные фигуры как объединения более простых фигур. Если построение графиков и фигур на них вызывает у вас затруднения, можете изучить раздел об основных элементарных функциях, геометрическом преобразовании графиков функций, а также построению графиков во время исследования функции.
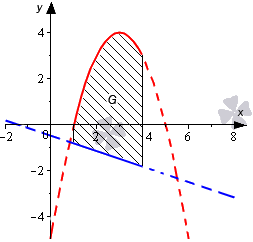
Необходимо определить площадь фигуры, которая ограничена параболой y=-x2+6x-5 и прямыми линиями y=-13x-12, x=1, x=4.
Решение
Изобразим линии на графике в декартовой системе координат.
На отрезке [1;4] график параболы y=-x2+6x-5 расположен выше прямой y=-13x-12. В связи с этим, для получения ответа используем формулу, полученную ранее, а также способ вычисления определенного интеграла по формуле Ньютона-Лейбница:
S(G)=∫14-x2+6x-5–13x-12dx==∫14-x2+193x-92dx=-13×3+196×2-92×14==-13·43+196·42-92·4–13·13+196·12-92·1==-643+1523-18+13-196+92=13
Ответ: S(G)=13
Рассмотрим более сложный пример.
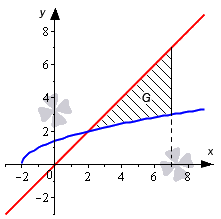
Необходимо вычислить площадь фигуры, которая ограничена линиями y=x+2, y=x, x=7.
Решение
В данном случае мы имеем только одну прямую линию, расположенную параллельно оси абсцисс. Это x=7. Это требует от нас найти второй предел интегрирования самостоятельно.
Построим график и нанесем на него линии, данные в условии задачи.
Имея график перед глазами, мы легко можем определить, что нижним пределом интегрирования будет абсцисса точки пересечения графика прямой y=x и полу параболы y=x+2. Для нахождения абсциссы используем равенства:
y=x+2ОДЗ: x≥-2×2=x+22×2-x-2=0D=(-1)2-4·1·(-2)=9×1=1+92=2∈ОДЗx2=1-92=-1∉ОДЗ
Получается, что абсциссой точки пересечения является x=2.
Обращаем ваше внимание на тот факт, что в общем примере на чертеже линии y=x+2 , y=x пересекаются в точке (2;2), поэтому такие подробные вычисления могут показаться излишними. Мы привели здесь такое подробное решение только потому, что в более сложных случаях решение может быть не таким очевидным. Это значит, что координаты пересечения линий лучше всегда вычислять аналитически.
На интервале [2;7] график функции y=x расположен выше графика функции y=x+2 . Применим формулу для вычисления площади:
S(G)=∫27(x-x+2)dx=x22-23·(x+2)3227==722-23·(7+2)32-222-23·2+232==492-18-2+163=596
Ответ: S(G)=596
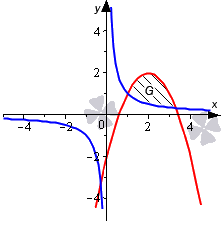
Необходимо вычислить площадь фигуры, которая ограничена графиками функций y=1x и y=-x2+4x-2.
Решение
Нанесем линии на график.
Определимся с пределами интегрирования. Для этого определим координаты точек пересечения линий, приравняв выражения 1x и -x2+4x-2. При условии, что x не равно нулю, равенство 1x=-x2+4x-2становится эквивалентным уравнению третьей степени -x3+4×2-2x-1=0 с целыми коэффициентами. Освежить в памяти алгоритм по решению таких уравнений мы можете, обратившись к разделу «Решение кубических уравнений».
Корнем этого уравнения является х=1: -13+4·12-2·1-1=0.
Разделив выражение -x3+4×2-2x-1 на двучлен x-1, получаем: -x3+4×2-2x-1⇔-(x-1)(x2-3x-1)=0
Оставшиеся корни мы можем найти из уравнения x2-3x-1=0:
x2-3x-1=0D=(-3)2-4·1·(-1)=13×1=3+132≈3.3 ; x2=3-132≈-0.3
Мы нашли интервал x∈1; 3+132, на котором фигура G заключена выше синей и ниже красной линии. Это помогает нам определить площадь фигуры:
S(G)=∫13+132-x2+4x-2-1xdx=-x33+2×2-2x-ln x13+132==-3+13233+2·3+1322-2·3+132-ln3+132—133+2·12-2·1-ln 1=7+133-ln3+132
Ответ: S(G)=7+133-ln3+132
Необходимо вычислить площадь фигуры, которая ограничена кривыми y=x3, y=-log2x+1 и осью абсцисс.
Решение
Нанесем все линии на график. Мы можем получить график функции y=-log2x+1 из графика y=log2x, если расположим его симметрично относительно оси абсцисс и поднимем на одну единицу вверх. Уравнение оси абсцисс у=0.
Обозначим точки пересечения линий.
Как видно из рисунка, графики функций y=x3 и y=0 пересекаются в точке (0;0). Так получается потому, что х=0 является единственным действительным корнем уравнения x3=0.
x=2 является единственным корнем уравнения -log2x+1=0, поэтому графики функций y=-log2x+1 и y=0 пересекаются в точке (2;0).
x=1 является единственным корнем уравнения x3=-log2x+1. В связи с этим графики функций y=x3 и y=-log2x+1 пересекаются в точке (1;1). Последнее утверждение может быть неочевидным, но уравнение x3=-log2x+1 не может иметь более одного корня, так как функция y=x3 является строго возрастающей, а функция y=-log2x+1 строго убывающей.
Дальнейшее решение предполагает несколько вариантов.
Вариант №1
Фигуру G мы можем представить как сумму двух криволинейных трапеций, расположенных выше оси абсцисс, первая из которых располагается ниже средней линии на отрезке x∈0; 1, а вторая ниже красной линии на отрезке x∈1;2. Это значит, что площадь будет равна S(G)=∫01x3dx+∫12(-log2x+1)dx.
Вариант №2
Фигуру G можно представить как разность двух фигур, первая из которых расположена выше оси абсцисс и ниже синей линии на отрезке x∈0; 2, а вторая между красной и синей линиями на отрезке x∈1; 2. Это позволяет нам найти площадь следующим образом:
S(G)=∫02x3dx-∫12×3-(-log2x+1)dx
В этом случае для нахождения площади придется использовать формулу вида S(G)=∫cd(g2(y)-g1(y))dy. Фактически, линии, которые ограничивают фигуру, можно представить в виде функций от аргумента y.
Разрешим уравнения y=x3 и -log2x+1 относительно x:
y=x3⇒x=y3y=-log2x+1⇒log2x=1-y⇒x=21-y
Получим искомую площадь:
S(G)=∫01(21-y-y3)dy=-21-yln 2-y4401==-21-1ln 2-144–21-0ln 2-044=-1ln 2-14+2ln 2=1ln 2-14
Ответ: S(G)=1ln 2-14
Необходимо вычислить площадь фигуры, которая ограничена линиями y=x, y=23x-3, y=-12x+4.
Решение
Красной линией нанесем на график линию, заданную функцией y=x. Синим цветом нанесем линию y=-12x+4, черным цветом обозначим линию y=23x-3.
Отметим точки пересечения.
Найдем точки пересечения графиков функций y=x и y=-12x+4 :
x=-12x+4ОДЗ: x≥0x=-12x+42⇒x=14×2-4x+16⇔x2-20x+64=0D=(-20)2-4·1·64=144×1=20+1442=16; x2=20-1442=4Проверка:x1=16=4, -12×1+4=-12·16+4=-4⇒x1=16 не является решением уравненияx2=4=2, -12×2+4=-12·4+4=2⇒x2=4 является решением уравниния ⇒(4; 2) точка пересечения y=x и y=-12x+4
Найдем точку пересечения графиков функций y=x и y=23x-3:
x=23x-3ОДЗ: x≥0x=23x-32⇔x=49×2-4x+9⇔4×2-45x+81=0D=(-45)2-4·4·81=729×1=45+7298=9, x245-7298=94Проверка:x1=9=3, 23×1-3=23·9-3=3⇒x1=9 является решением уравнения ⇒(9; 3) точка пересечания y=x и y=23x-3×2=94=32, 23×1-3=23·94-3=-32⇒x2=94 не является решением уравнения
Найдем точку пересечения линий y=-12x+4 и y=23x-3:
-12x+4=23x-3⇔-3x+24=4x-18⇔7x=42⇔x=6-12·6+4=23·6-3=1⇒(6; 1) точка пересечения y=-12x+4 и y=23x-3
Дальше мы можем продолжить вычисления двумя способами.
Способ №1
Представим площадь искомой фигуры как сумму площадей отдельных фигур.
Тогда площадь фигуры равна:
S(G)=∫46x–12x+4dx+∫69x-23x-3dx==23×32+x24-4×46+23×32-x23+3×69==23·632+624-4·6-23·432+424-4·4++23·932-923+3·9-23·632-623+3·6==-253+46+-46+12=113
Способ №2
Площадь исходной фигуры можно представить как сумму двух других фигур.
Тогда решим уравнение линии относительно x, а только после этого применим формулу вычисления площади фигуры.
y=x⇒x=y2 красная линияy=23x-3⇒x=32y+92 черная линияy=-12x+4⇒x=-2y+8 синяя линия
Таким образом, площадь равна:
S(G)=∫1232y+92–2y+8dy+∫2332y+92-y2dy==∫1272y-72dy+∫2332y+92-y2dy==74y2-74y12+-y33+3y24+92y23=74·22-74·2-74·12-74·1++-333+3·324+92·3–233+3·224+92·2==74+2312=113
Как видите, значения совпадают.
Ответ: S(G)=113
Итоги
Для нахождения площади фигуры, которая ограничена заданными линиями нам необходимо построить линии на плоскости, найти точки их пересечения, применить формулу для нахождения площади. В данном разделе мы рассмотрели наиболее часто встречающиеся варианты задач.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Пример1. Вычислить
площадь фигуры, ограниченной линиями: х + 2у – 4 = 0, у = 0, х = -3, и х = 2
Выполним построение фигуры (см. рис.) Строим
прямую х + 2у – 4 = 0 по двум точкам А(4;0) и В(0;2). Выразив у через х,
получим у = -0,5х + 2. По формуле (1), где f(x) = -0,5х + 2, а = -3, в = 2,
находим
S = = [-0,25=11,25 кв. ед
Пример 2. Вычислить площадь
фигуры, ограниченной линиями: х – 2у + 4 = 0, х + у – 5 = 0 и у = 0.
Решение. Выполним построение фигуры.
Построим прямую х – 2у + 4 = 0: у = 0, х = – 4, А(-4; 0); х = 0,
у = 2, В(0; 2).
Построим прямую х + у – 5 = 0: у = 0, х = 5, С(5; 0), х = 0, у =
5, D(0; 5).
Найдем точку пересечения прямых, решив систему уравнений:
х = 2, у = 3; М(2; 3).
Для вычисления искомой площади разобьем треугольник АМС на два
треугольника АМN и NМС, так как при изменении х от А до N площадь ограничена
прямой , а при изменении х от N до С – прямой
Для треугольника АМN имеем: ; у = 0,5х + 2, т.
е. f(x) = 0,5х + 2, a = – 4, b = 2.
Для треугольника NМС имеем: y = – x + 5, т. е. f(x) = – x + 5, a
= 2, b = 5.
Вычислив площадь каждого из треугольников и сложив результаты,
находим:
кв. ед.
кв. ед.
= 9 + 4, 5 = 13,5 кв. ед. Проверка: = 0,5АС = 0,5 кв. ед.
Пример 3. Вычислить площадь фигуры,
ограниченной линиями: y = x2, y =
0, x = 2, x = 3.
В данном случае требуется вычислить площадь криволинейной
трапеции, ограниченной параболой y = x2,
прямыми x = 2 и x = 3и осью Ох(см. рис.) По формуле (1) находим площадь
криволинейной трапеции
= = 6кв. ед.
Пример 4. Вычислить площадь
фигуры, ограниченной линиями: у = – x2 +
4 и у = 0
Выполним построение фигуры. Искомая площадь заключена между
параболой у = – x2 +
4 и осью Ох.
Найдем точки пересечения параболы с осью Ох.
Полагая у = 0, найдем х = Так как данная фигура симметрична относительно оси
Оу, то вычислим площадь фигуры, расположенной справа от оси Оу, и полученный
результат удвоим: = +4x]кв. ед. 2 = 2 кв. ед.
Пример 5. Вычислить площадь
фигуры, ограниченной линиями: y2 =
x, yx = 1, x = 4
Здесь требуется вычислить площадь криволинейной трапеции,
ограниченной верхней ветвью параболыy2 =
x, осью Ох и прямыми x = 1иx = 4 (см. рис.)
По формуле (1), где f(x) = a = 1 и b = 4 имеем =
( = кв. ед.
Пример 6.Вычислить
площадь фигуры, ограниченной линиями:y = sinx, y = 0, x = 0, x= .
Искомая площадь ограничена полуволной синусоиды и осью Ох (см.
рис.).
Имеем – cosx = – cos = 1 + 1 = 2 кв. ед.
Пример 7. Вычислить площадь
фигуры, ограниченной линиями: y = – 6х, у = 0 и х = 4.
Фигура расположена под осью Ох (см. рис.).
Следовательно, её площадь находим по формуле (3)
= =
Пример 8. Вычислить
площадь фигуры, ограниченной линиями:y = и х = 2. Кривую y = построим по точкам
(см. рис.). Таким образом, площадь фигуры находим по формуле (4 )

= = + = 1
Пример 9. Вычислить
площадь фигуры, ограниченной линиями:
х2 +
у2 = r2.
Здесь требуется вычислить площадь, ограниченную окружностью х2 +
у2 = r2,
т. е. площадь круга радиуса r с центром в начале координат. Найдем четвертую
часть этой площади, взяв пределы интегрирования от 0
доr; имеем: 1 =
= [
Следовательно, 1 =
Пример 10. Вычислить площадь
фигуры, ограниченной линиями: у= х2 и
у = 2х
Данная фигура ограничена параболой у= х2 и
прямой у = 2х (см. рис.) Для определения точек пересечения заданных линий решим
систему уравнений:х2 –
2х = 0 х = 0 и х = 2
Используя для нахождения площади формулу (5),
получим
= [x2 –
=
Пример 7. Вычислить площадь фигуры, ограниченной линиями: 7x2 –
9y + 9 = 0 и 5x2 –
9y + 27 = 0.
Запишем уравнения парабол в виде у =
Построим эти параболы.
Для нахождения точек их пересечения решим
систему.Так как фигура симметрична относительно оси Оу, то найдем половину её
площади, взяв пределы интегрирования от 0 до 3, и результат удвоим:1 = = =
41 =
8
Задания для самостоятельной работы
Вычислить площадь фигуры, ограниченной линиями:
1. у = х+
3х и у = 0 2. у = 6х – х и
у = х + 4
3.y = x; y = ; y = 0; x = 2; 4.у = хи
у = -3х 5. y = x2 –
6x +9; y = x2 + 4x + 4; y = 0;
Группа 2.
1. у = х–
4х + 3 и у = 0
2. у = 4 – хи
у = х + 2
3. y = y = 2x; y = ;
4. у = х+
2 и у = 6
5. y = x2 –
6x +9; y = x2 + 4x + 4; y = 0;
Группа 3.
1. у = 8х – 4х и
у = 0
2. у = хи
у = 4х – 3
3. у = хи
у = -3х
4. y =x; y = ; y = 0; x = 2;
5. y = x2 –
6x +9; y = x2 + 4x + 4; y = 0;
Группа4.
1. у = х–
6х + 5 и у = 0
2. у = х+
1 и у = 3 – х
3. у = х и
у = 2х
4. у = ; у = 0,5х
5. y = y = 2x; y = ;









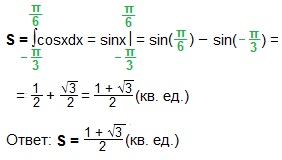

























 где
где  — некоторое число.
— некоторое число.

 , ограниченной графиками функций
, ограниченной графиками функций