Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Формула (формулы) площади круга
Найти площадь круга можно разными способами, в зависимости от известных данных.
По радиусу
Если дан только радиус, то площадь составит произведение константы Пи на квадрат радиуса. Расчёт будет по формуле (где r – радиус, а π – константа, равная 3,1415…):
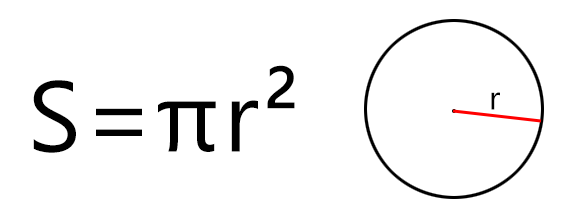
Например, если радиус равен 2 метра, то площадь круг можно вычислить так S = 3,14 × 22 = 3,14 × 4 = 12,56 м2 (квадратных метров).
Через диаметр
Если известен диаметр, то площадь круга будет равняться одной четвёртой произведения Пи и квадрата диаметра. Формула площади круга будет такой (где d – диаметр, а π – константа, равная 3,1415…):
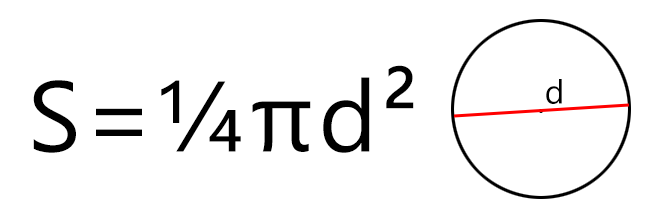
К примеру, если диаметр круга (площадь поверхности пиццы) составляет 35 сантиметров, то площадь такого круга будет равна S = ¼ × 3,14 × 352 = ¼ × 3,14 × 1225 = 962 см2 (квадратных сантиметра).
Через длину окружности
Если мы знаем только длину окружности (периметр круга), то рассчитать площадь фигуры можно по формуле (где L – длина окружности, а π – константа, равная 3,1415…):
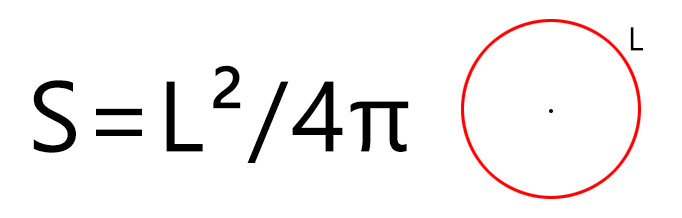
Например, если длинна окружности составляет 120 мм, тогда площадь круга будет равна S = 1202 / (4 × 3,14) = 14 400 / (4 × 3,14) = 1146,5 мм2 (квадратных миллиметров).
Какие термины используются для поиска площади круга?
Для вычисления площади круга, в формулах были использованы следующие термины, значение которых нужно знать, чтобы точно понимать принципы расчета.
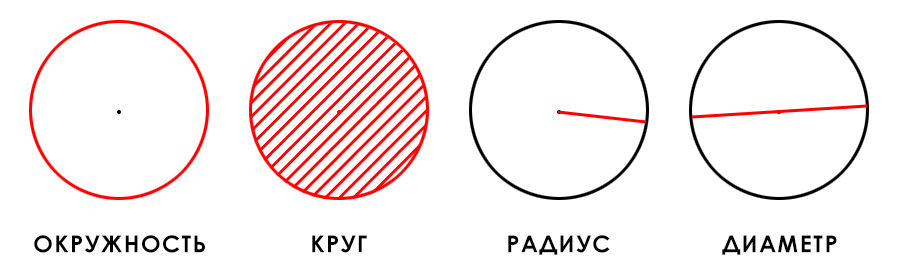
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.
Диаметр — отрезок, соединяющий две точки на окружности и проходящий через центр окружности. Диаметр равен двум радиусам.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Число π (пи) — математическая постоянная, равная отношению длины окружности к её диаметру. Пи равняется примерно 3,14.
Площадь круга и размеры пицц
Люди не всегда верно сопоставляют площадь круга и диаметры. К примеру, сможете ли вы ответить:

Что больше: 2 пиццы диаметром 25 см или 1 пицца диаметром 40 см?
Интуитивно кажется, что 2 пиццы, так как в сумме их радиусы дают 50 сантиметров, что больше, чем 40. Однако это неправильный вывод, так как сравнивать нужно не сумму диаметров, а сумму квадратов диаметров. То есть:
- 252 + 252 = 625 + 625 = 1250
- 402 = 1600
Так как ¼π является константой, то можно сравнивать только квадраты диаметров. Получается, что пицца 40 см больше, чем даже 2 пиццы размером 25 см. А вот если диаметр пиццы составляет 35 см, то 352 = 1225, и в этом случае 2 пиццы по 25 см будут иметь бОльшую площадь.
Площади усеченных частей круга
А также полезно знать следующие геометрические элементы, связанные с кругами и окружностями:
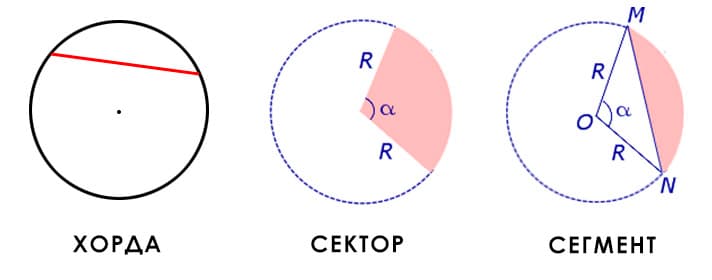
Хорда — отрезок, соединяющий любые две точки окружности.
Сектор — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Сектор является частью круга, а его площадь относится к площади круга так же, как и длина окружности сектора к длине всей окружности. Поэтому площадь сектора равна площади круга, умноженной на отношение длинны окружности сектора к длине окружности всего круга.
Но площадь сектора можно вычислить и по более простой формуле. Она равна длине дуги сектора, умноженной на половину радиуса:
S = sr/2
где S — площадь сектора, r — радиус круга.
Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой.
Площадь сегмента можно найти по формулам:
S = r2sinα/ 2
где S — площадь сегмента, sinα — синус угла двух между радиусов до концов хорды, r — радиус круга.
Часто задаваемые вопросы о площади круга?
И конечно, стоит ответить на некоторые вопросы, которые возникают во время расчетов.
Входит ли окружность (периметр) в площадь круга?
Да, входит, ведь кругом являются все точки, удаленные от центра круга на расстояние, которое не превышает радиус.
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть разнообразные калькуляторы, в частности калькуляторы: длины окружности, диаметра и площади круга. Для последней калькулятор находится на данной странице.
Хватит ли только диаметра, только радиуса или только длинны окружности для расчета площади круга?
Да, хватит чего-то одного, так как все 3 сущности можно вывести одну из другой, например, диаметр равен двум радиусам, а длина окружности – это диаметр, умноженный на число Пи.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Кто впервые научился вычислять площадь круга?
Гиппократ Хиосский (не тот, в честь которого назвали клятву) первым сформулировал, что площадь круга пропорциональна квадрату его диаметра. Евдокс Книдский в IV веке до н. э. строго доказал это утверждение. А Архимед в III веке до н. э. нашёл число Пи и продемонстрировал, что оно чуть меньше, чем 3 и 1/7.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
- Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Как рассчитать площадь круга
На данной странице калькулятор поможет рассчитать площадь круга онлайн. Для расчета задайте радиус, диаметр или длину окружности.
Круг – множество точек плоскости, удаленных от заданной точки этой плоскости (центр круг) на расстояние, не превышающее заданное (радиус круга).
Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.
Через радиус
Формула для нахождения площади круга через радиус:
π – константа равная (3.14); r – радиус круга.
Через диаметр
Формула для нахождения площади круга через диаметр:
π – константа равная (3.14); d – диаметр.
Через длину окружности

Формула для нахождения площади круга через длину окружности:
π – константа равная (3.14); l – длина окружности.
Найти площадь круга поможет калькулятор онлайн, который быстро и точно вычислит искомую величину. Площадь круга можно считать через диаметр или радиус. Здесь есть 2 калькулятора которыми мы рассчитываем площадь круга через диаметр и через радиус.
Калькулятор площади круга через диаметр
Калькулятор площади круга через радиус
Расчет площади круга на калькуляторе онлайн
Расчет площади круга пожалуй самый популярный вопрос в сети. Этот расчет может пригодиться практически любому человеку, начиная от школьника и заканчивая инженером. Поэтому мы тоже решили обязательно добавить на наш сайт точный калькулятор площади круга. Просто введите диаметр или радиус круга, нажмите на кнопку «Рассчитать» и мгновенно получите результат. Даже нажимать на неё не обязательно, всё на автомате. Результаты выводятся в нужных вам единицах измерения.
Площадь круга в основном считается двумя способами, а именно:
- площадь круга через диаметр
- площадь круга через радиус
Каким именно способом пользоваться решать вам. Он зависит от конкретной задачи и имеющихся исходных данных (размеров).
Наш онлайн-калькулятор площади круга удобен тем, что можно выбрать различные единицы измерения диаметра круга и рассчитанной площади круга. Стоит только переключиться и всё будет тут же пересчитано. К тому же у него очень хорошая точность, в чём вы можете легко убедиться сами.
И еще, имейте ввиду, что калькулятор округляет результат до 3-х знаков после запятой. Для обычных расчётов этого вполне достаточно. Если понадобится еще большая точность, напишите об этим в комментариях.
Формула площади круга через диаметр
S = π * D2 / 4 , где
S — площадь круга,
D — диаметр круга,
π — число «Пи».
Формула площади круга через радиус
S = π * R2 , где
S — площадь круга,
R — радиус круга,
π — математическая константа.
Как видите формулы для расчёта площадей круга очень простые, однако лучше всего площадь круга вычислит онлайн калькулятор. В таком случае будет меньше ошибок и не будет путаницы в единицах измерения.
Таблица площади круга в зависимости от диаметра
| Диаметр круга, см | Площадь круга, см2 |
|---|---|
| 1 | 0,79 |
| 2 | 3,14 |
| 3 | 7,07 |
| 4 | 12,57 |
| 5 | 19,64 |
| 10 | 78,54 |
| 15 | 176,72 |
| 20 | 314,16 |
| 25 | 480,87 |
| 50 | 1963,50 |
| 100 | 7853,98 |
| 200 | 31415,93 |
Пригодилось? Добавьте в закладки чтобы не потерять или нажмите на «поделиться».
Было полезно? Поделитесь с друзьями!
![]()
Условие:
Диаметр окружности 2 см. Найти площадь круга, ограниченного этой окружностью.
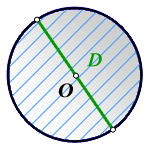
Дано:
Диаметр окружности, D = 2 см
Пояснение к рисунку:
O – центр окружности
Решение
Используем формулу площади круга через диаметр.
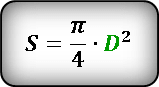
Подставим значения и вычислим результат.
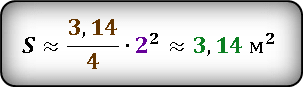
Ответ:
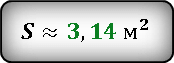
![]() Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14
Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14
Калькулятор для расчета площади круга через радиус
![]()
- Подробности
-
Опубликовано: 04 сентября 2017
-
Обновлено: 13 августа 2021
Окружность – это замкнутая линия, причем расстояние от любой точки, находящейся на этой линии, до центра окружности одинаково. Кругом является внутренняя часть окружности.
Онлайн-калькулятор площади круга
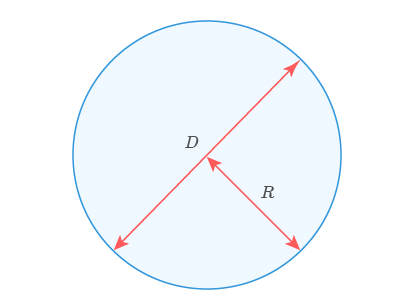
Тот самый отрезок, который соединяет выбранную точку на окружности с ее центром, называется радиусом RR.
Длина радиуса, взятая в двойном размере, называется диаметром окружности DD.
То есть D=2RD=2R.
Как найти площадь круга
Площадь круга можно найти двумя способами:
- используя радиус круга,
- используя диаметр круга.
Остановимся чуть подробнее на каждом способе и рассмотрим несколько примеров.
Формула площади круга через радиус круга
Сначала разберем общий случай.
Пусть нам дана окружность OO произвольного радиуса R.R. Площадь круга через радиус вычисляется при помощи формулы
S=πR2S=pi R^2,
где πpi – число «Пи», выражающее отношение длины окружности к ее диаметру и численно равное около 3,143,14,
RR – радиус нашей окружности.
Теперь, чтобы было более понятно, рассмотрим пару практических примеров.
Найдите площадь круга, радиус которого равен 6 см.
Ответ дайте, округленный до целого числа.
Решение:
Пользуемся нашей формулой для вычисления площади круга и получаем:
S=πR2=3,14⋅6⋅6=3,14⋅36=113.S=pi R^2=3,14cdot 6 cdot 6=3,14 cdot 36=113.
Ответ: 113 см2.
Формула площади круга через диаметр
Рассмотрим сначала обобщенный случай без использования цифр.
Формула вычисления площади круга с помощью диаметра немного отличается от формулы, в которой мы использовали радиус. Но ответ остается, безусловно, таким же.
Итак, наша формула выглядит следующим образом:
S=πD24S=pi frac{D^2}{4}
Давайте разберемся, откуда она вообще взялась.
Для начала выразим радиус через диаметр. Получаем R=D2R=frac{D}{2}, затем подставляем полученное выражение в нашу исходную формулу S=πR2S=pi R^2 и получаем результат: S=πD222S=pi frac{D^2}{2^2}, далее упрощаем и выходим на окончательный ответ S=πD24S=pi frac{D^2}{4}.
Найти площадь круга, если известно, что четвертая часть диаметра равна 2,5 см.
Решение:
Находим диаметр:
D4=2,5.frac{D}{4} =2,5.
Отсюда,
D=2,5⋅4=10.D=2,5 cdot 4=10.
Подставляем значения в формулу:
S=πD24=3,14⋅1024=3,14⋅1004=3,14⋅25=78,5S=pi frac{D^2}{4} =3,14 cdot frac{10^2}{4} =3,14 cdot frac{100}{4} =3,14 cdot 25=78,5
Ответ: 78,5 см2.
Пример решения задачи посложнее.
Имеется два круга. Площадь первого 153,86153,86 см2. Найдите площадь второго круга, радиус которого в 22 раза больше радиуса первого круга.
Решение:
Для решения задачи нам в первую очередь нужно найти радиус первого круга. Из формулы S=πR2S=pi R^2 находим, что R=SπR=sqrt{frac{S}{pi}}.
R=153.863.14=49=7.R=sqrt{frac{153.86}{3.14}}=sqrt{49} = 7.
Радиус второго круга равен 7⋅2=14.7 cdot 2=14.
Наконец, найдем площадь этого круга: S=πR2=3.14⋅142=3,14⋅196=615,44.S=pi R^2=3.14cdot14^2=3,14 cdot 196=615,44.
Ответ: 615,44615,44 см2.
Ищете специалиста, который сможет написать контрольную работу на заказ для вас? Наши эксперты подбирают индивидуальный подход к каждому клиенту!
