Как найти площадь круга если известен периметр

Калькулятор площади окружности (круга) через длину (периметр)

При помощи данного калькулятора можно вычислить площадь окружности зная ее длину (периметр).

Длина окружности P

Формула для вычисления площади окружность выглядит следующим образом:

S = πR² при вычислении через радиус

S = πD²/4 при вычислении через диаметр

Таким образом для нахождения окружности нам необходимо знать либо ее диаметр D, либо радиус R.
Зная длину (периметр) окружности проще всего установить диаметр, т.к. диаметр окружности в π раз меньше ее длины. Соответственно для установления диаметра окружности необходимо ее длину разделить на π.

D = P/π

Найдя диаметр окружности, мы можем узнать площадь круга через формулу, указанную выше:

S = πD²/4

В рассмотренном случае, мы для нахождения площади круга, использовали две формулы. Но как же нам найти площадь используя только одну формулу? Давайте постараемся создать ее сами.
В формулу S = πD²/4 вместо D подставим значение P/π соответственно получаем

S = (π/4)*(P/π)² = (π*P²)/(π²*4) = (π*P²)/(π*π*4) = P²/(π*4)

или

S = P²/(π*4)

Где:
S – площадь окружности.
P – длина окружности.
D – диаметр окружности
π – математическая постоянная, константа, которая примерно равна 3.14

Например, нужно вычислить площадь круглой колонны. Диаметр не измеришь. Какие формулы использовать, чтобы высчитать её площадь. Формула площади: S = П*r² Формула длины окружности (периметра): P = 2*П*r П – это число Пи: 3.14… Из окружности находим радиус: r = P/2П И подставляем это в формулу площади: S = П*(P/2П)² = П*P²/4П² Если я правильно раскрыл скобки со степенями, то: П – сокращаются и остаётся: S = P²/4П автор вопроса выбрал этот ответ лучшим Ксарф­акс [156K] 5 лет назад  Для того, чтобы найти площадь круга через длину окружности, нужно сначала вспомнить формулы, по которым вычисляется: 1) Длина окружности. 2) Площадь круга. Итак, формула для длины окружности: l =2πR. Что касается площади круга, то она вычисляется по формуле: C = πR². Здесь R – это радиус, а π – число Пи, которое равно 3,14. Если известна длина окружности, то легко выразить её радиус. После этого остаётся лишь подставить полученное значение в формулу для площади круга. R = l / 2π. C = π * (l / 2π)² = l² / 4π. Пример Дана длина окружности l = 20 см. Нужно найти площадь круга. C = l² / 4π = (20 * 20) / (4 * 3,14) = 400 / 12,56 = 31,85 см. Таким образом, если длина окружности равна 20 см., то площадь круга будет составлять 31,85 см. Урани­я [155K] 2 года назад  Площадь круга можно легко рассчитать по известной формуле, в которую входит радиус круга (или окружности, что одно и то же): S = πR²; Где R – это радиус окружности, а число π – это неизменяемая величина, равная – 3,14 В свою очередь, длина окружности тоже рассчитывается через его радиус: С = 2πR; Отсюда следует, что выразив радиус окружности из последней формулы (R = C/2π) , и подставив его в первую формулу, мы получим формулу, в которой площадь круга будет выражена через его длину окружности: S = π(C/ 2π)². После возведения в квадрат и необходимых сокращений, получим окончательную искомую формулу: S = C²/4π Эта именно та формула, в которой площадь (S) круга выражена через его длину окружности (С). Чёрна­я Луна [265K] 4 года назад  Выедим формулу для нахождения площади круга, при условии использования длинны окружности. Как известно, формула площади круга: S = 2πR²; Формула периметра окружности или длинны окружности вычисляется по формуле: С = 2πR; R – это радиус окружности, число π – всегда равно 3,14. Радиус необходим нам для того, чтобы найти площадь. А зная длину окружности мы можем вычислить радиус. R = C/2π Заменяем эту форму на радиус в формуле по нахождению площади окружности: S = 2π(C/2π)²; После раскрытия скобок и сокращения получаем следующую формулу: S = C²/4π По конечной формуле можно найти площадь круга, зная его периметр. Для этого есть формула вычисления площади окружности – где S – искомая площадь, C – длина окружности, П – число равное 3,14. Допустим длина окружности равна 75 сантиметрам. Возводим ее в квадрат, получаем 5625. Теперь получаем 5625/4П. Сокращаем выражение до минимума – 5625/4=1406 Теперь это значение выглядит как 1406/п = 447 квадратных сантиметров. Это стандартная геометрическая задача. Радиус колонны вычисляется из формулы длины окружности L = 2 * пи * R, откуда R = 0.5 * L / пи Площадь находим по формуле S = пи * R^2 = пи * (0.5 * L / пи)^2 = 0.25 * пи * L^2. Аналогично можно посчитать и объем колонны, зная лишь длину окружности и высоту. V = 0.25 * пи * L^2 * H, где H – высота колонны. -Irink­a- [281K] 4 года назад  Выведенная формула для нахождения S окружности, зная длину его окружности: Так как площадь круга равняется Подставляя в формулу значение радиуса, мы получаем формулу нахождения площади круга, через длину окружности. Допустим длина l=8 см, число π=3,14 Получается, что площадь круга будет равна 5 см². Бекки Шарп [71.2K] 3 года назад  Есть такая всем известная константа Пи (3,1425), она равна длине окружности поделенной на длину диаметра. То есть зная длину, мы всегда найдем диаметр. А зная диаметр мы можем посчитать площадь круга по известной формуле. Знаете ответ?

Площадь круга: как найти, формулы

О чем эта статья:

площадь, 6 класс, 9 класс, ЕГЭ/ОГЭ

Определение основных понятий

Прежде чем погрузиться в последовательность расчетов и узнать, чему равна площадь круга, важно выяснить разницу между понятиями окружности и круга.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.

Если говорить простым языком, окружность — это замкнутая линия, как, например, кольцо и шина. Круг — плоская фигура, ограниченная окружностью, как монетка или крышка люка.

Формула вычисления площади круга

Давайте разберем несколько формул расчета площади круга. Поехали!

Площадь круга через радиус

S = π × r 2 , где r — это радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.

Площадь круга через диаметр

S = d 2 : 4 × π, где d — это диаметр.

Площадь круга через длину окружности

S = L 2 ​ : (4 × π), где L — это длина окружности.

Популярные единицы измерения площади:

• квадратный миллиметр (мм 2 );
• квадратный сантиметр (см 2 );
• квадратный дециметр (дм 2 );
• квадратный метр (м 2 );
• квадратный километр (км 2 );
• гектар (га).

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Задачи. Определить площадь круга

Мы разобрали три формулы для вычисления площади круга. А теперь тренироваться — поехали!

Задание 1. Как найти площадь круга по диаметру, если значение радиуса равно 6 см.

Диаметр окружности равен двум радиусам.

Используем формулу: S = π × d 2 : 4.

Подставим известные значения: S = 3,14 × 12 2 : 4.

Ответ: 113,04 см 2 .

Задание 2. Найти площадь круга, если известен диаметр, равный 90 мм.

Используем формулу: S = π × d 2 : 4.

Подставим известные значения: S = 3,14 × 90 2 : 4.

Ответ: 6358,5 мм 2 .

Задание 3. Найти длину окружности при радиусе 3 см.

Отношение длины окружности к диаметру является постоянным числом.

Получается: L = d × π.

Так как диаметр равен двум радиусам, то формула длины окружности примет вид: L = 2 × π × r.

Подставим значение радиуса: L = 2 × 3,14 × 3.

Ответ: 18,84 см 2 .

Формулы площади круга и расчет онлайн

Здесь вы можете рассчитать площадь круга по известным параметрам. Для вычисления достаточно знать радиус, диаметр круга или длину его окружности.

Окружность и круг — в чём отличие?

Часто понятия круг и окружность путают, хотя это разные вещи. Окружность — это замкнутая линия, а круг — это плоская фигура, ограниченная окружностью. Таким образом, гимнастический обруч или колечко — это окружности, а монета или вкусный блин — это круги.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от одной заданной точки — центра окружности.

Круг — бесконечное множество точек на плоскости, которые удалены от заданной точки, называемой центром круга, на значение, не превышающее заданного неотрицательного числа, называемого радиусом этого круга.

Окружность и круг

Площадь круга. Калькулятор и формулы

Нужно быстро определить площадь круга, если известен периметр, радиус или длина? Тогда воспользуйтесь этим простым онлайн-калькулятором. Заполните одну любую ячейку в калькуляторе окружности и нажмите на кнопку расчета. Остальные величины посчитаются автоматически. Также напротив значений будут выведены формулы вычислений.
После того как будет найден радиус окружности, можно воспользоваться двумя нижерасположенными калькуляторами и найти величины сегмента и сектора круга.
Обратите внимание! Если у сегмента известны только площадь или периметр, то произвести вычисления не получится. Для расчета остальных значений сегмента, помимо его площади и периметра также должны быть известны длина хорды, длина дуги или высота.

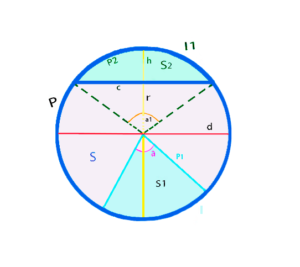
Калькулятор окружности:

Достаточно заполнить только одну ячейку — остальное калькулятор посчитает сам.

[spoiler title=”источники:”]

http://mnogoformul.ru/formuly-ploshhadi-kruga-i-raschet-onlayn

http://calcon.ru/ploshhad-kruga-kalkulyator-i-formuly/

[/spoiler]

Поскольку радиус тесно связан отношениями с диаметром и длиной окружности, то путем нехитрых замен можно также вычислить площадь круга через диаметр или длину окружности .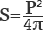

Диаметр – это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно разделить его обратно на два.
Длина окружности представляет собой удвоенное произведение радиуса и числа π: P=2πr, обратным методом получаем, что радиус равен длине окружности, разделенной на его множитель.

Калькулятор окружности:

Достаточно заполнить только одну ячейку — остальное калькулятор посчитает сам.

Калькулятор сектора окружности:

Достаточно ввести только одно значение и указать радиус окружности — остальное калькулятор посчитает сам.

Калькулятор сегмента окружности:

Достаточно ввести только одно* значение и указать радиус окружности — остальное калькулятор посчитает сам.
Исключения:
* – при известном периметре (P2) нужно дополнительно указать длину дуги (l1) или хорды (c).
* – при известной площади (S2) нужно дополнительно указать длину хорды (c) или высоты (h).

Округление:

* – обязательно заполнить