Расчет площади круга — это не только учебная задача для школьников шестого класса. Круглых предметов довольно много и в реальной жизни, а необходимость посчитать их площадь хотя и не так часто, но возникает. Например, это может потребоваться для определения количества краски для ремонта круглой столешницы или для расчета площади остекления дома, спроектированного и построенного в готическом стиле.
Сложность вычисления площади круга связана с тем, что практически во всех формулах встречается иррациональное число пи, которое в обычных расчетах принимается равным 3,14. Даже если вы с детства неплохо владеете устным счетом, вычислить в уме площадь круга, радиус которого выражается дробным числом, будет довольно затруднительно. Но теперь это и не нужно, поскольку мы разработали для вас удобный сервис, который сделает все расчеты за несколько мгновений. Причем необязательно пересчитывать известные вам размеры конструкции так, чтобы получить значение радиуса в явном виде. Наш калькулятор умеет считать площадь круга практически по всем параметрам, которые могут быть известны на практике.
Расчет площади круга по его радиусу
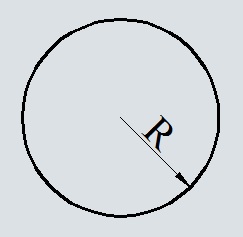
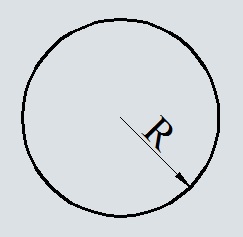
Начнем с классической формулы: S = π · R2, где S — площадь круга, R — его радиус, а π — то самое число пи. В нашем онлайн-калькуляторе оно задано с точностью до пяти знаков после запятой, поэтому он выполняет немного более точные вычисления. Если вы знаете радиус круга, введите его в соответствующем окне на первой вкладке. Результат будет выведен сразу же под ним.
Формула площади круга через диаметр
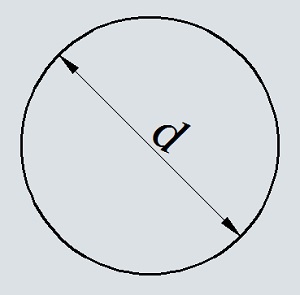
Если вам известен диаметр круга, можно разделить его пополам и подставить в предыдущую формулу. Но можно поступить еще проще. Перейдите на вторую вкладку и введите диаметр D в качестве исходных данных. Калькулятор использует формулу S = π · D2 / 4 и рассчитывает площадь круга прямо в процессе вашего ввода. Если после вывода результата вы измените значение диаметра, результат пересчитается автоматически.
Площадь круга через длину окружности
Для начала на всякий случай определимся с терминологией: окружность — это линия, каждая точка которой удалена на одинаковое расстояние от центра, а круг — это все, что находится внутри нее. Таким образом, окружность представляет собой внешнюю границу круга. Ее длина равна 2 · π · R (за R по-прежнему обозначаем радиус круга и окружности). Теоретически отсюда можно вычислить радиус и посчитать площадь круга по классической формуле. Но, опять же, есть более простой способ: воспользоваться нашим онлайн-калькулятором и ввести известную длину окружности, не выполняя ненужных промежуточных действий. Результат, как и всегда, будет выведен мгновенно.
Расчет площади круга по стороне вписанного квадрата
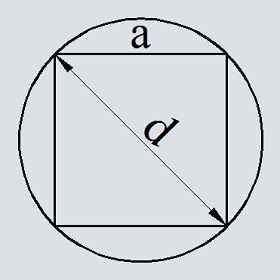
Эта задача может встретиться при разработке дизайн-проекта или при необходимости закрыть предмет квадратного сечения кругом минимальной площади. Известная сторона квадрата также довольно легко переводится в радиус описанного вокруг него круга, но калькулятор считает его площадь так, чтобы вам не пришлось делать никаких промежуточных вычислений. Для справки: используется формула S = π · a2 / 2, где a — сторона квадрата.
Как найти площадь круга, если известна сторона описанного вокруг него квадрата
Предположим, вы хотите купить бассейн, под который у вас выделен квадратный участок известных размеров. Вполне закономерно желание поставить резервуар максимальной емкости, которая определяется его высотой и площадью. То есть нужно найти площадь круга максимального радиуса, вписанного в квадрат, что и приводит к необходимости ее расчета через сторону этого квадрата. Нетрудно заметить, что задача сводится к вычислению площади круга по известному диаметру, так как сторона описанного вокруг него квадрата как раз и есть его диаметр. Но мы сделали для этого варианта отдельную вкладку, чтобы не заставлять вас запоминать ненужную информацию. Просто вводите длину стороны квадрата и получайте результат точно так же, как и во всех предыдущих случаях.
Вычисление площади круга через диагональ описанного квадрата
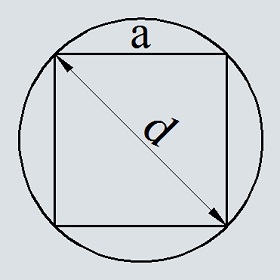
Если в условиях предыдущего примера вы знаете не сторону квадрата, а его диагональ d, вам тоже не потребуется ничего пересчитывать. В калькулятор уже заложена формула S = π · d2 / 8, в соответствии с которой он покажет результат, как только вы введете длину диагонали на нужной вкладке. Как всегда, площадь круга вычисляется автоматически и выводится заново каждый раз, когда вы меняете значение диагонали.
Расчет площади круга по площади описанного вокруг него квадрата
Как наиболее рационально использовать квадратную заготовку известной площади для изготовления круглой детали? Очевидно, что необходимо вырезать из нее круг максимального диаметра. Площадь такого круга вы можете посчитать с помощью нашего калькулятора, задав на соответствующей вкладке известную площадь квадрата. Формула расчета имеет вид: Sкр = Sкв · π / 4.
Условия использования онлайн-калькулятора расчета площади круга
Вы можете пользоваться данным сервисом совершено бесплатно. Количество расчетов не ограничено, калькулятор запускается из любого браузера, ничего устанавливать на ваш компьютер не нужно. Если наш сайт оказался полезным для вас, напишите об этом в комментариях и не забудьте сохранить его в закладках, чтобы иметь возможность выполнять любые математические вычисления, не отходя от компьютера.
Как рассчитать площадь круга
На данной странице калькулятор поможет рассчитать площадь круга онлайн. Для расчета задайте радиус, диаметр или длину окружности.
Круг – множество точек плоскости, удаленных от заданной точки этой плоскости (центр круг) на расстояние, не превышающее заданное (радиус круга).
Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.
Площадь круга: как найти, формулы
О чем эта статья:
площадь, 6 класс, 9 класс, ЕГЭ/ОГЭ
Определение основных понятий
Прежде чем погрузиться в последовательность расчетов и узнать, чему равна площадь круга, важно выяснить разницу между понятиями окружности и круга.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.
Если говорить простым языком, окружность — это замкнутая линия, как, например, кольцо и шина. Круг — плоская фигура, ограниченная окружностью, как монетка или крышка люка.
Формула вычисления площади круга
Давайте разберем несколько формул расчета площади круга. Поехали!
Площадь круга через радиус
S = π × r 2 , где r — это радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.
Площадь круга через диаметр
S = d 2 : 4 × π, где d — это диаметр.
Площадь круга через длину окружности
S = L 2 : (4 × π), где L — это длина окружности.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Задачи. Определить площадь круга
Мы разобрали три формулы для вычисления площади круга. А теперь тренироваться — поехали!
Задание 1. Как найти площадь круга по диаметру, если значение радиуса равно 6 см.
Диаметр окружности равен двум радиусам.
Используем формулу: S = π × d 2 : 4.
Подставим известные значения: S = 3,14 × 12 2 : 4.
Ответ: 113,04 см 2 .
Задание 2. Найти площадь круга, если известен диаметр, равный 90 мм.
Используем формулу: S = π × d 2 : 4.
Подставим известные значения: S = 3,14 × 90 2 : 4.
Ответ: 6358,5 мм 2 .
Задание 3. Найти длину окружности при радиусе 3 см.
Отношение длины окружности к диаметру является постоянным числом.
Получается: L = d × π.
Так как диаметр равен двум радиусам, то формула длины окружности примет вид: L = 2 × π × r.
Подставим значение радиуса: L = 2 × 3,14 × 3.
Ответ: 18,84 см 2 .
Площадь круга
Круг – это плоская фигура, которая представляет собой множество точек равноудаленных от центра. Все они находятся на одинаковом расстоянии и образуют собой окружность. 
Отрезок, который соединяет центр круга с точками его окружности, называется радиусом. В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром. Формула площади круга рассчитывается с помощью математической константы – числа π..
Это интересно: Число π. представляет собой соотношение длины окружности к длине ее диаметра и является постоянной величиной. Значение π = 3,1415926 получило применение после работ Л. Эйлера в 1737 г.
Площадь окружности можно вычислить через константу π. и радиус окружности. Формула площади круга через радиус выглядит так:
Существует формула площади круга через диаметр. Она также широко применяется для вычисления необходимых параметров. Данные формулы можно использовать для нахождения площади треугольника по площади описанной окружности.
Знания стандартных формул расчета площади круга помогут в дальнейшем легко определять площадь секторов и легко находить недостающие величины.
Мы уже знаем, что формула площади круга рассчитывается через произведение постоянной величины π на квадрат радиуса окружности. Радиус можно выразить через длину окружности и подставить выражение в формулу площади круга через длину окружности: 
Теперь подставим это равенство в формулу расчета площади круга и получим формулу нахождения площади круга, через длину окружности
Площадь круга описанного вокруг квадрата

Очень легко можно найти площадь круга описанного вокруг квадрата.
Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a ее можно найти по теореме Пифагора: 

После того, как найдем диагональ – мы сможем рассчитать радиус: 
И после подставим все в основную формулу площади круга описанного вокруг квадрата:
Зная несколько простых правил и теорему Пифагора, мы смогли рассчитать площадь описанной вокруг квадрата окружности.
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/ploshad-kruga
http://2mb.ru/matematika/geometriya/ploshhad-kruga/
[/spoiler]
Как найти площадь круга? Сначала найдите радиус. Учитесь решать простые и сложные задачи.
Содержание
- Площадь круга: формула через радиус, диаметр, длину окружности, примеры решения задач
- Формула нахождения площади круга через радиус:
- Формула нахождения S-площади круга через D-диаметр:
- Нахождение S круга, если известна длина окружности:
- Площадь круга, вписанного в квадрат: формула, примеры решения задач
- Задача №1: Известна сторона квадратной фигуры, которая равна 6 сантиметров. Найдите S-площадь вписанной окружности.
- Задача №2: Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см.
- Площадь круга, описанного около квадрата: формула, примеры решения задач
- Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: формула, примеры решения задач
- Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач
- Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач
- Площадь круга, описанного около прямоугольной и равнобедренной трапеции: формула, примеры решения задач
- Видео: Математика | Вычисление площадей круга и его частей
Круг — это замкнутая кривая. Любая точка на линии окружности будет находиться на одинаковом расстоянии от центральной точки. Круг — это плоская фигура, поэтому решать задачи с нахождением площади просто. В этой статье мы рассмотрим, как найти площадь круга, вписанного в треугольник, трапецию, квадрат, и описанного около этих фигур.
Площадь круга: формула через радиус, диаметр, длину окружности, примеры решения задач
Чтобы найти площадь данной фигуры, нужно знать, что такое радиус, диаметр и число π.
Радиус R — это расстояние, ограниченное центром окружности. Длины всех R-радиусов одной окружности будут равными.
Диаметр D — это линия между двумя любыми точками окружности, которая проходит через центральную точку. Длина этого отрезка равна длине R-радиуса, умноженной на 2.
Число π — это неизменная величина, которая равна 3,1415926. В математике обычно это число округляется до 3,14.
Формула нахождения площади круга через радиус:
Примеры решения заданий по нахождению S-площади круга через R-радиус:
————————————————————————————————————————
Задача: Найдите площадь окружности, если ее радиус равен 7 см.
Решение: S=πR², S=3,14*7², S=3,14*49=153,86 см².
Ответ: Площадь окружности равна 153,86 см².
Формула нахождения S-площади круга через D-диаметр:
Примеры решения заданий по нахождению S, если известен D:
————————————————————————————————————————-
Задача: Найдите S круга, если его D равен 10 см.
Решение: P=π*d²/4, P=3,14*10²/4=3,14*100/4=314/4=78,5 см².
Ответ: Площадь плоской круглой фигуры равна 78,5 см².
Нахождение S круга, если известна длина окружности:
Сначала находим, чему равен радиус. Длина окружности рассчитывается по формуле: L=2πR, соответственно радиус R будет равен L/2π. Теперь находим площадь круга по формуле через R.
Рассмотрим решение на примере задачи:
———————————————————————————————————————-
Задача: Найдите площадь круга, если известна длина окружности L — 12 см.
Решение: Сначала находим радиус: R=L/2π=12/2*3,14=12/6,28=1,91.
Теперь находим площадь через радиус: S=πR²=3,14*1,91²=3,14*3,65=11,46 см².
Ответ: Площадь круга равна 11,46 см².
Площадь круга, вписанного в квадрат: формула, примеры решения задач
Найти площадь круга, вписанного в квадрат просто. Сторона квадрата — это диаметр круга. Чтобы найти радиус, нужно сторону разделить на 2.
Формула нахождения площади круга, вписанного в квадрат:
Примеры решения задач по нахождению площади круга, вписанного в квадрат:
———————————————————————————————————————
Задача №1: Известна сторона квадратной фигуры, которая равна 6 сантиметров. Найдите S-площадь вписанной окружности.
Решение: S=π(a/2)²=3,14(6/2)²=3,14*9=28,26 см².
Ответ: Площадь плоской круглой фигуры равна 28,26 см².
————————————————————————————————————————
Задача №2: Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см.
Решайте так: Сначала найдем R=a/2=4/2=2 см.
Теперь найдем площадь окружности S=3,14*2²=3,14*4=12,56 см².
Ответ: Площадь плоской круглой фигуры равна 12,56 см².
Площадь круга, описанного около квадрата: формула, примеры решения задач
Немного сложнее находить площадь круглой фигуры, описанной около квадрата. Но, зная формулу, можно быстро подсчитать данное значение.
Формула нахождения S круга, описанного около квадратной фигуры:
Примеры решения заданий по нахождению площади окружности, описанной около квадратной фигуры:
Задача
Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: формула, примеры решения задач
Окружность, которая вписана в треугольную фигуру — это круг, который касается всех трех сторон треугольника. В любую треугольную фигуру можно вписать круг, но только один. Центром круга будет точка пересечения биссектрис углов треугольника.
Формула нахождения площади круга, вписанного в равнобедренный треугольник:
Когда будет известен радиус, площадь можно вычислить по формуле: S=πR².
Формула нахождения площади круга, вписанного в прямоугольный треугольник:
Примеры решения заданий:
Задача №1
Если в этой задаче нужно найти еще и площадь круга с радиусом 4 см, то сделать это можно по формуле: S=πR²
Задача №2
Решение:
Теперь, когда известен радиус, можно найти площадь круга через радиус. Формулу смотрите выше по тексту.
Задача №3
Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач
Все формулы по нахождению площади круга сводятся к тому, что сначала нужно найти его радиус. Когда известен радиус, то найти площадь просто, как было описано выше.
Площадь круга, описанного около прямоугольного и равнобедренного треугольника находится по такой формуле:
Примеры решения задач:
Вот еще пример решения задачи с использованием формулы Герона.
Решать подобные задачи сложно, но их можно осилить, если знать все формулы. Такие задачи школьники решают в 9 классе.
Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач
У равнобедренной трапеции две стороны равны. У прямоугольной трапеции один угол равен 90º. Рассмотрим, как найти площадь круга, вписанного в прямоугольную и равнобедренную трапецию на примере решения задач.
Например, в равнобедренную трапецию вписана окружность, которая в точке касания делит одну сторону на отрезки m и n.
Для решения этой задачи нужно использовать такие формулы:
Нахождение площади окружности, вписанной в прямоугольную трапецию, производится по следующей формуле:
Если известна боковая сторона, то можно найти радиус через это значение. Высота боковой стороны трапеции равна диаметру окружности, а радиус — это половина диаметра. Соответственно, радиус равен R=d/2.
Примеры решения задач:
Площадь круга, описанного около прямоугольной и равнобедренной трапеции: формула, примеры решения задач
Трапецию можно вписать в окружность, когда сумма ее противолежащих углов равна 180º. Поэтому вписать можно только равнобокую трапецию. Радиус для вычисления площадь круга, описанного около прямоугольной или равнобедренной трапеции, рассчитывается по таким формулам:
Примеры решения задач:
Решение: Большое основание в данном случае проходит через центр, так как в окружность вписана равнобедренная трапеция. Центр делит это основание ровно пополам. Если основание АВ равно 12, тогда радиус R можно найти так: R=12/2=6.
Ответ: Радиус равен 6.
В геометрии важно знать формулы. Но все их невозможно запомнить, поэтому даже на многих экзаменах разрешается пользоваться специальным формуляром. Однако важно уметь находить правильную формулу для решения той или иной задачи. Тренируйтесь в решении разных задач на нахождение радиуса и площади окружности, чтобы уметь правильно подставлять формулы и получать точные ответы.
Видео: Математика | Вычисление площадей круга и его частей
Как рассчитать площадь круга
На данной странице калькулятор поможет рассчитать площадь круга онлайн. Для расчета задайте радиус, диаметр или длину окружности.
Круг – множество точек плоскости, удаленных от заданной точки этой плоскости (центр круг) на расстояние, не превышающее заданное (радиус круга).
Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.
Через радиус
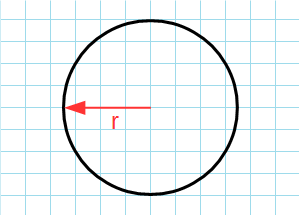
Формула для нахождения площади круга через радиус:
π – константа равная (3.14); r – радиус круга.
Через диаметр
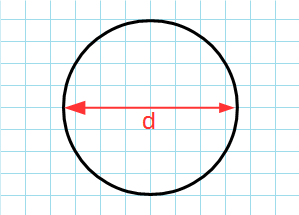
Формула для нахождения площади круга через диаметр:
π – константа равная (3.14); d – диаметр.
Через длину окружности

Формула для нахождения площади круга через длину окружности:
π – константа равная (3.14); l – длина окружности.
- Площадь круга по радиусу
- Площадь круга по диаметру
- Площадь круга по длине окружности
- Площадь круга по стороне квадрата вписанного в этот круг
- Площадь круга по площади квадрата вписанного в этот круг
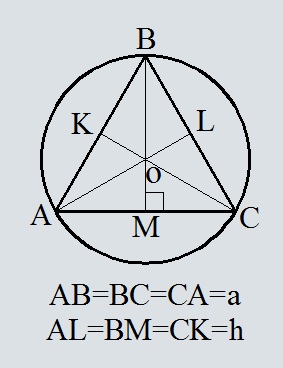
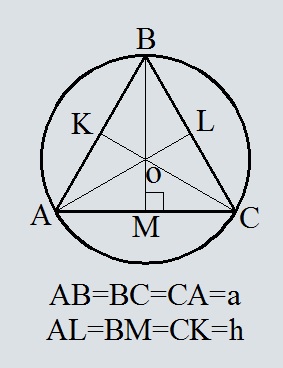
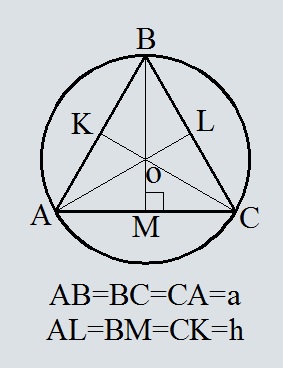
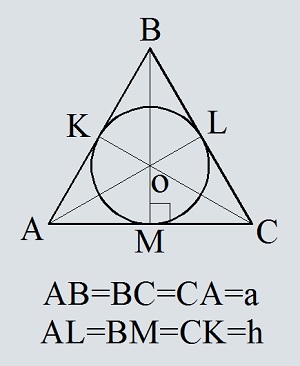
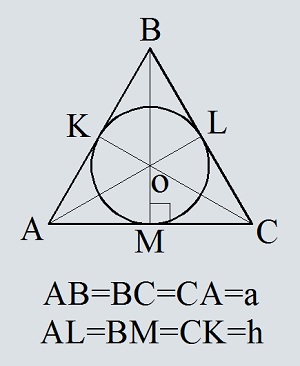
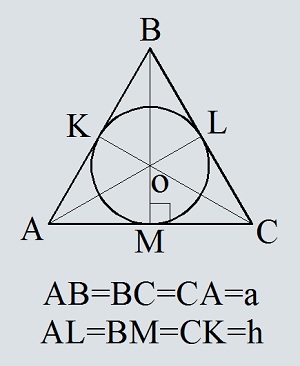
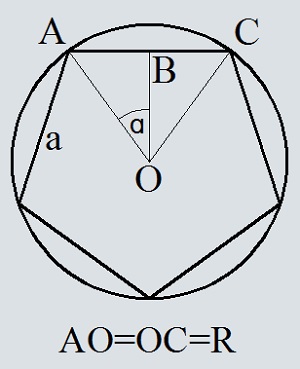
- Площадь круга описанного около равностороннего треугольника, по стороне треугольника
- Площадь круга описанного около равностороннего треугольника, по высоте треугольника
- Площадь круга описанного около равностороннего треугольника, по площади треугольника
- Площадь круга вписанного в равносторонний треугольник, по стороне треугольника
- Площадь круга вписанного в равносторонний треугольник, по высоте треугольника
- Площадь круга вписанного в равносторонний треугольник, по площади треугольника
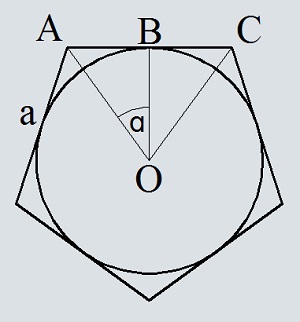
- Площадь круга вписанного в правильный многоугольник, по стороне и количеству вершин многоугольника
- Площадь круга описанного около правильного многоугольника, по стороне и количеству вершин многоугольника
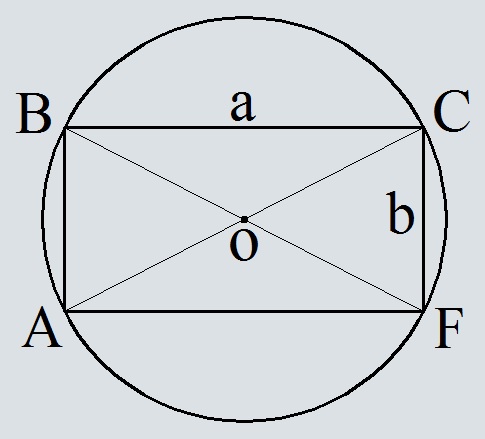
- Площадь круга описанного около прямоугольника, вычисленная по сторонам прямоугольника
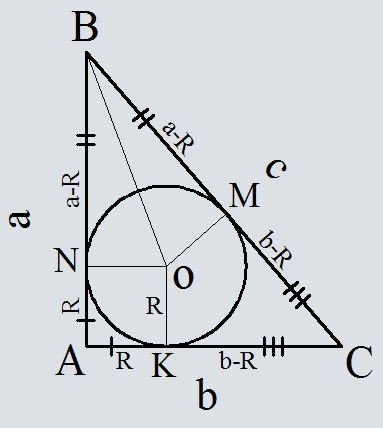
- Площадь круга вписанного в прямоугольный треугольник, по катетам треугольника
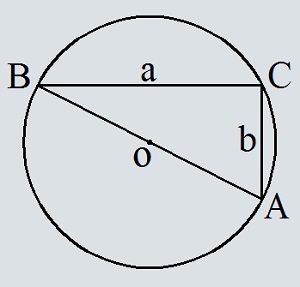
- Площадь круга описанного около прямоугольного треугольника, по катетам треугольника
Площадь круга по радиусу
Формула площади круга по радиусу
S=πR2
Где S – площадь круга,
R – радиус круга,
π=3.14
Площадь круга по диаметру
Формула площади круга по диаметру
Где S – площадь круга,
d – диаметр круга,
π=3.14
Площадь круга по длине окружности
Введите длину окружности c
Формула площади круга по длине окружности
Где S – площадь круга,
c – длина окружности,
π=3.14
Площадь круга по стороне квадрата вписанного в этот круг
Введите сторону квадрата a
Формула площади круга по стороне квадрата вписанного в этот круг
Где S – площадь круга,
a – сторона квадрата,
π=3.14
Площадь круга по площади квадрата вписанного в этот круг
Введите площадь квадрата Sкв
Формула площади круга по площади квадрата вписанного в этот круг
Где Sкр – площадь круга,
Sкв – площадь квадрата,
π=3.14
Площадь круга описанного около равностороннего треугольника, по стороне треугольника
Введите сторону равностороннего треугольника a
Формула площади круга описанного около равностороннего треугольника, по стороне треугольника
Где S – площадь круга,
a – сторона треугольника,
π=3.14
Площадь круга описанного около равностороннего треугольника, по высоте треугольника
Введите высоту равностороннего треугольника h
Формула площади круга описанного около равностороннего треугольника, по высоте треугольника
Где S – площадь круга,
h – высота треугольника,
π=3.14
Площадь круга описанного около равностороннего треугольника, по площади треугольника
Введите площадь равностороннего треугольника Sтр
Формула площади круга описанного около равностороннего треугольника, по площади треугольника
Где Sкр – площадь круга,
Sтр – площадь треугольника,
π=3.14
Площадь круга вписанного в равносторонний треугольник, по стороне треугольника
Введите сторону равностороннего треугольника a
Формула площади круга вписанного в равносторонний треугольник, по стороне треугольника
Где S – площадь круга,
a – сторона треугольника,
π=3.14
Площадь круга вписанного в равносторонний треугольник, по высоте треугольника
Введите высоту равностороннего треугольника h
Формула площади круга вписанного в равносторонний треугольник, по высоте треугольника
Где S – площадь круга,
h – высота треугольника,
π=3.14
Площадь круга вписанного в равносторонний треугольник, по площади треугольника
Введите площадь равностороннего треугольника Sтр
Формула площади круга вписанного в равносторонний треугольник, по площади треугольника
Где Sкр – площадь круга,
Sтр – площадь треугольника,
π=3.14
Площадь круга вписанного в правильный многоугольник, по стороне и количеству вершин многоугольника
Введите количество вершин многоугольника n
Введите длину стороны многоугольника a
Формула площади круга вписанного в правильный многоугольник, по стороне и количеству вершин многоугольника
Где a – сторона многоугольника,
n – количество вершин многоугольника,
π=3.14
Площадь круга описанного около правильного многоугольника, по стороне и количеству вершин многоугольника
Введите количество вершин многоугольника n
Введите длину стороны многоугольника a
Формула площади круга описанного около правильного многоугольника, по стороне и количеству вершин многоугольника
Где a – сторона многоугольника,
n – количество вершин многоугольника,
π=3.14
Площадь круга описанного около прямоугольника, вычисленная по сторонам прямоугольника
Введите сторону a
Введите сторону b
Формула площади круга описанного около прямоугольника, вычисленная по сторонам прямоугольника
Где a, b – стороны прямоугольника,
π=3.14
Площадь круга вписанного в прямоугольный треугольник, по катетам треугольника
Введите катет a
Введите катет b
Формула площади круга вписанного в прямоугольный треугольник, по катетам треугольника
Где a, b – катеты прямоугольного треугольника,
π=3.14
Площадь круга описанного около прямоугольного треугольника, по катетам треугольника
Введите катет a
Введите катет b
Формула площади круга вписанного в равносторонний треугольник, по площади треугольника
Где a, b – катеты прямоугольного треугольника,
π=3.14