Радиус окружности, описанной около правильного шестиугольника
Содержание:
- Что такое окружность, описанная около правильного шестиугольника
- Как найти радиус, формула
- Свойства окружности, описанной около шестиугольника
- Площадь круга, ограниченного описанной окружностью
- Пример расчета радиуса окружности, описанной около шестиугольника
Что такое окружность, описанная около правильного шестиугольника
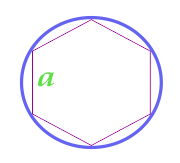
Правильный шестиугольник — выпуклый шестиугольник, у которого все стороны и углы равны.
Описанная около многоугольника окружность — это окружность, которая содержит все вершины выпуклого многоугольника. Ее центром является точка пересечения срединных перпендикуляров к сторонам многоугольника, обычно её обозначают прописной буквой О.
Как найти радиус, формула
Для расчетов используем формулу радиуса окружности, описанной около правильного многоугольника.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Формула 1
(R=frac a{2sinleft(frac{360^0}{2n}right)})
где R — радиус описанной окружности правильного многоугольника,
а — длина стороны многоугольника,
n — количество сторон (или вершин) многоугольника.
Подставим в формулу значение n=6.
(R=frac a{2sinleft(frac{360^0}{2n}right)}=R=frac a{2sinleft(frac{360^0}{2·6}right)}=frac a{2sinleft(frac{360^0}{12}right)}=frac a{2sin30^0}.)
Так как (sin30^0=frac12), то (R=frac a{2sin30^0}=frac a{2·frac12}=frac a1). Получаем формулу радиуса окружности, описанной около правильного шестиугольника:
Формула 2
R=a
где R — радиус описанной окружности,
а — сторона правильного шестиугольника.
Примечание 1
Эту же формулу модно найти и другим способом. Биссектрисы углов правильного шестиугольника разбивают его на шесть равных равносторонних треугольников. Точка пересечения биссектрис у правильного шестиугольника совпадает с точкой пересечения срединных перпендикуляров и является центром описанной окружности. Расстояние между центром окружности и вершиной шестиугольника равно радиусу описанной окружности и стороне равностороннего треугольника. Этот отрезок также равен стороне шестиугольника.
Свойства окружности, описанной около шестиугольника
- У правильного шестиугольника центры вписанной и описанной окружностей совпадают.
- Диаметр описанной окружности совпадает с большей диагональю правильного шестиугольника и равен его удвоенной стороне.
Площадь круга, ограниченного описанной окружностью
Чтобы вычислить площадь круга, ограниченного описанной окружностью правильного шестиугольника, используем стандартную формулу площади круга.
Формула 3
(S=π·r^2)
где S — площадь круга,
π — коэффициент, число π,
r — радиус круга.
Так как радиус круга равен стороне правильного шестиугольника, около которого описана окружность, получаем формулу:
Формула 4
(S=π·а^2)
где S — площадь круга,
π — коэффициент, число π,
а — сторона правильного шестиугольника.
Пример расчета радиуса окружности, описанной около шестиугольника
Задача
Дано: около правильного шестиугольника описана окружность. Меньшая диагональ правильного шестиугольника равна (5sqrt3 см.)
Найти: радиус описанной окружности.
Решение: Обозначим сторону правильного шестиугольника как а. Тогда его меньшая диагональ будет (аsqrt3 см). Следовательно, а=5 см. Радиус окружности, описанной около правильного шестиугольника равен его стороне. R=5 см.
Ответ: 5 см.
Насколько полезной была для вас статья?
Рейтинг: 5.00 (Голосов: 1)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
 Главная
Главная  Учёба
Учёба  Площадь круга
Площадь круга  Площадь круга описанного около правильного шестиугольника
Площадь круга описанного около правильного шестиугольника
Площадь круга описанного около правильного шестиугольника
Формула расчёта площади круга описанного около правильного шестиугольника Вам необходимо указать сторону правильного шестиугольника (a).
Расчёт происходит по формуле 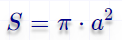 .
.
Формула расчёта площади круга описанного около правильного шестиугольника Вам необходимо указать сторону правильного шестиугольника (a).
Расчёт происходит по формуле 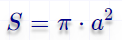 .
.
 Другая Формула
Другая Формула
Понравилась страница? Поделитесь ссылкой в социальных сетях. Поддержите проект!
Нет комментариев.
КАК НАЙТИ ПЛОЩАДЬ КРУГА, описанного около правильного шестиугольника ???
Ученик
(21),
закрыт
14 лет назад
Червь Кольчатый
Гуру
(3674)
14 лет назад
Его сторона равна радиусу описанной окружности (соединив противоположные вершины шестиугольника, заметим, что эти три диагонали пересекутся в одной точке и разделят друг друга пополам – при этом получится 6 маленких правильных треугольничков. Точка пересечения этих диагоналей и олкажется центром, а расстояние от неё до вершин будет равно стороне)
Ну а зная радиус круга, остаётся найти его площадь по формуле pi*r^2
Сообщения без ответов | Активные темы
Найдите площадь круга, описанного около шестиугольника
Модераторы: Prokop, mad_math
| Автор | Сообщение | ||
|---|---|---|---|
|
magahalk |
Заголовок сообщения: Найдите площадь круга, описанного около шестиугольника
|
||
|
Площадь правильного шестиугольника равна [math]24sqrt{3}[/math] см^2 . Найдите площадь круга, описанного около шестиугольника
|
||
| Вернуться к началу |
|
||
|
Misha1 |
Заголовок сообщения: Re: Найдите площадь круга, описанного около шестиугольника
|
|
Решается задача довольно просто.(см. рис.)
|
|
| Вернуться к началу |
|
|
ALEXIN |
Заголовок сообщения: Re: Найдите площадь круга, описанного около шестиугольника
|
|
Если рассуждать — то из 6-угольника получается 6 треугольников и площадь любого равна 4*sqrt 3= [4 * 4*(sqrt 3)/2]/2. Здесь (sqrt 3)/2 = cos60 градусов. По смыслу 4*sqrt 3 = [ Х * Х *(sqrt 3)/2]/2 Отношение площади 6-угольника к площади круга:
|
|
| Вернуться к началу |
|
| За это сообщение пользователю ALEXIN “Спасибо” сказали: summer_ |
|
|
ALEXIN |
Заголовок сообщения: Re: Найдите площадь круга, описанного около шестиугольника
|
|
|
|
| Вернуться к началу |
|
| За это сообщение пользователю ALEXIN “Спасибо” сказали: summer_ |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Сторона многоугольника описанного около окружности
в форуме Геометрия |
SimplyProgrammer |
1 |
175 |
19 окт 2016, 15:47 |
|
Найти высоту косинуса наименьшего объема описанного около ша
в форуме Дифференциальное исчисление |
apple-wolf |
1 |
242 |
19 мар 2019, 14:15 |
|
Отношение периметра описанного круга к стороне идеального тр
в форуме Теория чисел |
HaI7I7y |
10 |
124 |
28 дек 2022, 17:18 |
|
Отношение периметра описанного круга к стороне квадрата
в форуме Теория чисел |
HaI7I7y |
2 |
79 |
28 дек 2022, 18:27 |
|
Найдите радиус окружности, описанной около треугольника
в форуме Геометрия |
golden cat |
2 |
122 |
11 май 2022, 19:04 |
|
Найдите радиус окружности, описанной около треугольника
в форуме Геометрия |
Alliance |
11 |
1399 |
08 апр 2014, 09:33 |
|
Площадь описанного четырёхугольника
в форуме Геометрия |
GeorgeB |
1 |
289 |
16 мар 2017, 23:38 |
|
Наименьшая площадь описанного четырехугольника
в форуме Дифференциальное исчисление |
anpe0681 |
5 |
610 |
17 окт 2017, 23:34 |
|
Найдите производную поля в положительном направлении круга
в форуме Векторный анализ и Теория поля |
Bosjak |
2 |
167 |
26 апр 2021, 00:53 |
|
Трапеция., описанная около нее окружность. найти площадь тра
в форуме Геометрия |
Someone0310 |
1 |
430 |
09 окт 2014, 17:29 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 7 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group
Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru
Русская поддержка phpBB
На этой странице вы найдете калькуляторы и формулы, которые помогут найти и рассчитать площадь правильного шестиугольника по стороне или радиусам вписанной и описанной окружностей.
Шестиугольник представляет собой многоугольник, к которого все внутренние углы равны 120 градусов, а все стороны равны между собой.
Содержание:
- калькулятор площади правильного шестиугольника
- формула площади правильного шестиугольника через длину стороны
- формула площади правильного шестиугольника через радиус вписанной окружности
- формула площади правильного шестиугольника через радиус описанной окружности
- формула площади правильного шестиугольника через периметр
- примеры задач
Формула площади правильного шестиугольника через длину стороны
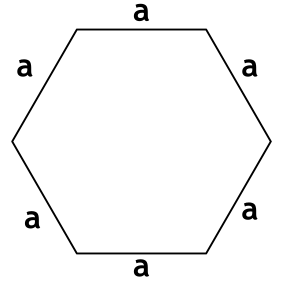
S = dfrac{3 sqrt{3} a^2}{2}
a – длина стороны шестиугольника
Формула площади правильного шестиугольника через радиус вписанной окружности
S = 2 sqrt{3}r^2
r – радиус вписанной окружности
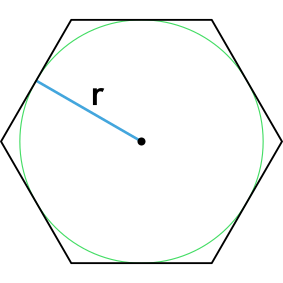
Формула площади правильного шестиугольника через радиус описанной окружности

S = dfrac{3 sqrt{3} R^2}{2}
R – радиус описанной окружности
Формула площади правильного шестиугольника через периметр

S = dfrac{P^2 sqrt{3}}{24}
P – периметр шестиугольника
Примеры задач на нахождение площади правильного шестиугольника
Задача 1
Найдите площадь правильного шестиугольника, радиус вписанной окружности которого равен 9 см.
Решение
Исходя из того, что из условия задачи нам известен радиус вписанной окружности, мы воспользуемся формулой.
S = 2 sqrt{3}r^2 = 2 sqrt{3} cdot 9^2 = 2 sqrt{3} cdot 81 = 162 sqrt{3} : см^2 approx 280.59223 : см^2
Ответ: 162 sqrt{3} : см^2 approx 280.59223 : см^2
Проверить правильность решения нам поможет калькулятор .
Задача 2
Найдите площадь правильного шестиугольника со стороной равной 1 см.
Решение
Для этой задачи нам подойдет формула.
S = dfrac{3 sqrt{3} a^2}{2} = dfrac{3 sqrt{3} cdot 1^2}{2} = dfrac{3 sqrt{3} cdot 1}{2} = dfrac{3 sqrt{3}}{2} : см^2 approx 2.59808 : см^2
Ответ: dfrac{3 sqrt{3}}{2} : см^2 approx 2.59808 : см^2
Проверим ответ .







