Площадь круга – это размер области внутри окружности, определенный в квадратных единицах измерения. Определять площадь круга можно по формулам, которые давно известны и использовались еще в Древнем мире для определения необходимого количества строительных материалов при построения зданий, амфитеатра и других архитектурных сооружений. В современном мире, с его быстрыми изменениями в архитектуре и в строительстве – определять площадь круга не менее важно. И в задачах алгебры и геометрии это умение пригодится.
Формулы площади круга
Площадь круга через радиус
В геометрии используются следующая формула для определения площади круга через радиус круга:
Здесь – площадь круга,
– радиус круга.
В формуле фигурирует – это постоянная величина, которая называется “число
” – это постоянная величина, которая часто используется в геометрии и в тригонометрии и означает отношение длины окружности к ее диаметру. Значение этого отношение получается постоянным, но не точным, и до сегодняшнего дня ученые стараются уточнить это значение. Приближенно “число
” равно 3,14. Хотя после цифры “4” еще бесконечное количество цифр:
Площадь круга измеряется в квадратных единицах длины: см2, м2, дм2, мм2, кв.ед. Однако, в физике площадь круга будет рассчитываться в СИ: м2. Иногда в задачах сразу указывается – в каких единицах следует рассчитать площадь круга.
Площадь круга через диаметр
Давайте получим формулу площади круга через диаметр.
Так как диаметр – это два радиуса, то, следовательно, радиус – это половина диаметра:
– диаметр круга.
Подставим это выражение для радиуса в формулу площади круга, получим:
Таким образом, нами получена формула площади круга через диаметр круга:
Площадь круга через длину окружности
Окружность – это граница круга. Зная длину этой границы мы можем рассчитать площадь круга. Итак, формула длины окружности: , тогда определим радиус и подставим его в формулу (1):
,
И формула площади круга через длину окружности:
Примеры решения задач
Задача 1
Найдите площадь круга, если известен его радиус см.
Решение: Для определения площади круга используем формулу (1):
см2. Сейчас мы имеем точное значение площади круга. Но если мы возьмем вместо
число 3,14, то получим приближенное значение площади круга:
см2.
Ответ: 78,5 см2.
Задача 2
Найдите площадь земельного участка, если известно, что форма участка – круг, а диаметр участка составляет 50 м.
Решение: Чтобы найти площадь земельного участка, мы должны рассчитать площадь круга с диаметром 50 м. Используем формулу (2):
м2.
Ответ: м2.
Задача 3
Длина границы земельного участка круглой формы равна 64 м. Найдите площадь участка.
Решение: граница участка круглой формы – это окружность. Тогда длина этой границы – это длина окружности. Площадь участка – площадь круга, которую мы определим по формуле (3) через длину окружности:
м2.
Ответ: м2.
Для того, чтобы определять площадь круга в задачах по геометрии вам нужно определить с тем, какие данные вам известны и использовать те формулы для определения площади круга, которые больше всего подходят.
Содержание:
Определение площади и объема:
В повседневной жизни нам довольно часто приходится иметь дело с определением таких величин, как площадь и объем. Представьте себе, что вам необходимо сделать ремонт в квартире (или доме): побелить стены и потолок, покрасить пол. Чтобы закупить необходимое количество материалов, нужно определить площадь поверхностей и объем краски.
Из уроков математики вам известно, как находить площадь некоторых фи-гур: квадрата, прямоугольника, параллелограмма.
|
Рис. 6.1. |
Рис. 6.2. |
Рис. 6.3 |
Площадь прямоугольника ABCD (рис. 6.1) вычисляется по формуле:
S = a · b, (6.1)
где a – ширина прямоугольника, b – высота.
Площадь параллелограмма ABCD (рис. 6.2) также находится по формуле 6.1. Площадь квадрата найти легко, поскольку его ширина и высота одинаковы:
S = a · a = a2 , (6.2)
Из рис. 6.1 видно, что площадь прямоугольного треугольника АBC можно найти по формуле:
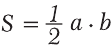
Проблема определения площади круга была решена еще в Древней Греции. Для этого нужно знать радиус круга и число «пи», приблизительное значение
которого π ≈ 3,14.
Площадь круга равняется
S = π · R2, (6.4) .
Значение числа 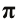
Вычисление объема простых фигур
Каждое тело занимает определенный объем. Чем большую часть пространства занимает тело, тем больше его объем. Объем обозначают буквой V (от volume – объем). Чтобы найти объем прямоугольного бруска или ящика (математики называют эту геометрическую фигуру параллелепипедом) со сторона-ми a, b и h, надо их перемножить (рис. 6.4):
|
Рис. 6.4. |
Рис. 6.5. |
|
V = a · b · h (6.4)
Поскольку S = a · b,
где S – это площадь основания ящика, то формулу (6.4) можно переписать и так:
V = S · h (6.5)
У куба все ребра равны, потому его объем равняется:
V = a · a · a = a3 (6.6)
Объем цилиндра (рис. 6.5) с радиусом основания R и высотой h можно также определить по формуле (6.5), то есть:
V = S · h = πR2 · h (6.7)
Объем шара (рис. 6.6)
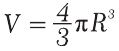
Единицы измерения объема
Поскольку длину сторон измеряют в единицах длины (метр, дециметр, сантиметр и т. д.), то единицы измерения объема – это единицы длины, возведенные в третью степень.
Куб с ребром 1 м имеет объем 1 м3 (один кубический метр). Один литр (1 л) по определению – это объем куба с ребром 1 дм (рис. 6.7), то есть 1 л = 1 дм3 (дециметр кубический). Один литр равен 1000 кубических сантиметров: 1 л = 1000 см3. Объем в один сантиметр кубический еще называют миллилитром, то есть тысячной частью литра (1 мл = 0,001 л).
Рис. 6.7. Один литр – это 1дм3
Напомним, что дециметр – это десятая часть метра, а сантиметр – сотая часть метра
Таблица 6.1
| 1 м3 = 1 000 л | 1 м3 = 1 000 000 см3 |
| 1 л = 1 дм3 | 1 л = 1000 см3 |
| 1 дм3 = 1 000 см3 | 1 л = 1 000 мл |
| 1 см3 = 1 мл | 1 мл = 0,001 л |
- Заказать решение задач по физике
Измерение объема тел неправильной формы
Прибор для измерения объема называют мензуркой, или мерным цилиндром (рис. 6.8). Мензурка – это прозрачный сосуд с нанесенными делениями, которые обозначают объем в миллилитрах. Дома у вас наверняка есть мерный стакан, то есть та же мензурка. Литровой или поллитровой банкой, или стаканом (250 мл) также можно пользоваться, если не нужна большая точность. С помощью мензурки можно определить объем жидкости и тела неправильной формы. Для этого в мензурку нужно налить воду и определить объем этой воды. Потом полностью погрузить тело в воду и запомнить новое значение объема. Разница измеренных значений равна объему тела.
Рис. 6.8. Деления мензурки определяют объем в миллилитрах (то есть в см3)
История:
 |
Существует легенда, согласно которой первым такой способ определения объема изобрел древнегреческий ученый Архимед. Произошло это во время размышлений над довольно сложной зада-чей, предложенной царем Гиероном. Идея решения возникла тогда, когда Архимед влез в ванну и заметил, что уровень воды поднялся. Ученый понял, что вытесненный объем воды как раз равен объему погруженного в нее тела. Восторженный Архимед выпрыгнул из ванны и выбежал на улицу с криком «Эврика! Эврика!», что в переводе с древнегреческого значит «На-шел! Нашел!». |
Итоги:
- Площадь тел правильной формы равна произведению основы на высоту и измеряется в квадратных единицах длины S = a · b.
- Объем тел правильной формы определяется как произведение площади основы на высоту и измеряется в кубических единицах V = S · h.
- Объем тел произвольной формы определяют с помощью мензурки
- Площадь круга определяют по формуле S = π · R2.
- Объем шара равен
.
- Связь физики с другими науками
- Макромир, мегамир и микромир в физике
- Пространство и время
- Что изучает механика в физике
- Единая физическая картина мира
- Физика и научно-технический прогресс
- Физические величины и их единицы измерения
- Точность измерений и погрешности
Круг – это плоская фигура, которая представляет собой множество точек равноудаленных от центра. Все они находятся на одинаковом расстоянии и образуют собой окружность.
Отрезок, который соединяет центр круга с точками его окружности, называется радиусом. В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром. Формула площади круга рассчитывается с помощью математической константы – числа π..
Это интересно: Число π. представляет собой соотношение длины окружности к длине ее диаметра и является постоянной величиной. Значение π = 3,1415926 получило применение после работ Л. Эйлера в 1737 г.
Площадь окружности можно вычислить через константу π. и радиус окружности. Формула площади круга через радиус выглядит так:
Рассмотрим пример расчета площади круга через радиус. Пусть дана окружность с радиусом R = 4 см. Найдем площадь фигуры.
Площадь нашей окружности будет равна 50,24 кв. см.
Существует формула площади круга через диаметр. Она также широко применяется для вычисления необходимых параметров. Данные формулы можно использовать для нахождения площади треугольника по площади описанной окружности.
Рассмотрим пример расчета площади круга через диаметр, зная его радиус. Пусть дана окружность с радиусом R = 4 см. Для начала найдем диаметр, который, как известно, в два раза больше радиуса.
Теперь используем данные для примера расчета площади круга по приведенной выше формуле:
Как видим, в результате получаем тот же ответ, что и при первых расчетах.
Знания стандартных формул расчета площади круга помогут в дальнейшем легко определять площадь секторов и легко находить недостающие величины.
Мы уже знаем, что формула площади круга рассчитывается через произведение постоянной величины π на квадрат радиуса окружности. Радиус можно выразить через длину окружности и подставить выражение в формулу площади круга через длину окружности:
Теперь подставим это равенство в формулу расчета площади круга и получим формулу нахождения площади круга, через длину окружности
Рассмотрим пример расчета площади круга через длину окружности. Пусть дана окружность с длиной l = 8 см. Подставим значение в выведенную формулу:
Итого площадь круга будет равна 5 кв. см.
Площадь круга описанного вокруг квадрата
Очень легко можно найти площадь круга описанного вокруг квадрата.
Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a ее можно найти по теореме Пифагора: 

После того, как найдем диагональ – мы сможем рассчитать радиус: 
И после подставим все в основную формулу площади круга описанного вокруг квадрата:
Рассмотрим пример расчета площади круга, описанного вокруг квадрата.
Задача: дан квадрат, вписанный в круг. Его сторона a = 4 см. Найдите площадь окружности.
Для начала рассчитаем длину диагонали d.
Теперь подставляем данные в формулу
Зная несколько простых правил и теорему Пифагора, мы смогли рассчитать площадь описанной вокруг квадрата окружности.
Как рассчитать площадь круга
На данной странице калькулятор поможет рассчитать площадь круга онлайн. Для расчета задайте радиус, диаметр или длину окружности.
Круг – множество точек плоскости, удаленных от заданной точки этой плоскости (центр круг) на расстояние, не превышающее заданное (радиус круга).
Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.
Через радиус
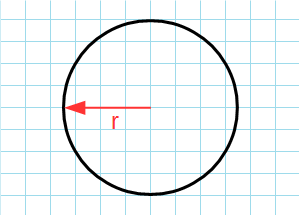
Формула для нахождения площади круга через радиус:
π – константа равная (3.14); r – радиус круга.
Через диаметр
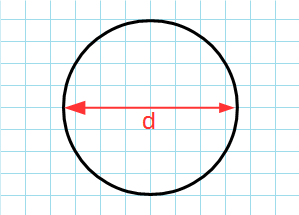
Формула для нахождения площади круга через диаметр:
π – константа равная (3.14); d – диаметр.
Через длину окружности

Формула для нахождения площади круга через длину окружности:
π – константа равная (3.14); l – длина окружности.
Загрузить PDF
Загрузить PDF
Некоторые учащиеся не понимают, как найти площадь круга по исходным данным. Для начала нужно запомнить формулу, по которой вычисляется площадь круга: 
-
1
Найдите радиус круга. Радиус – это отрезок, соединяющий центр круга с любой точкой внешней окружности круга. Радиус можно измерить в любом направлении: он будет одним и тем же. Радиус также равен половине диаметра круга. Диаметр – это отрезок, который проходит через центр круга и соединяет две точки внешней окружности круга.[1]
- Как правило, значение радиуса дано в условиях задачи. Довольно трудно найти точный центр круга, если только он не обозначен на круге, который нарисован на бумаге.
- Например, радиус круга равен 6 см.
-
2
Возведите радиус в квадрат. Формула для вычисления площади круга:
, где
– радиус, который возведен во вторую степень (в квадрат).[2]
-
3
Полученный результат умножьте на число Пи. Это число обозначается греческой буквой
и представляет собой математическую константу, которая характеризует взаимосвязь радиуса и площади круга. Число Пи приблизительно равно 3,14. Точное значение числа Пи включает бесконечное количество цифр. Иногда ответ (площадь круга) записывается с постоянной
.[3]
- В нашем примере (r = 6 см) площадь вычисляется так:
-
4
Запишите ответ. Помните, что площадь измеряется в квадратных единицах. Если радиус дан в сантиметрах, площадь измеряется в квадратных сантиметрах. Если радиус дан в миллиметрах, площадь измеряется в квадратных миллиметрах. Уточните у преподавателя, нужно ли представить ответ с постоянной
или в числовой форме, используя приблизительное значение числа Пи. Если требование не ясно, запишите оба варианта ответа.[4]
- В нашем примере (r = 6 см) S = 36
см2 или S = 113,04 см2.
Реклама
- В нашем примере (r = 6 см) S = 36
-
1
Измерьте или запишите диаметр. В некоторых задачах радиус не дан. Вместо радиуса указывается диаметр. Если диаметр нарисован на бумаге, измерьте его с помощью линейки. Скорее всего, числовое значение диаметра будет задано.
- Например, диаметр круга равен 20 мм.
-
2
Разделите диаметр пополам. Помните, что диаметр равен удвоенному радиусу. Поэтому разделите любое значение диаметра на 2, чтобы найти радиус.
- Таким образом, если диаметр круга равен 20 мм, то радиус круга равен 20/2 = 10 мм.
-
3
-
4
Запишите ответ. Помните, что площадь измеряется в квадратных единицах. В нашем примере диаметр дан в миллиметрах, поэтому радиус тоже измеряется в миллиметрах, а площадь в квадратных миллиметрах. В нашем примере S =
мм2.
- Также ответ можно представить в численной форме, используя вместо
приблизительное значение 3,14. В этом случае S = (100)(3,14) = 314 мм2.
Реклама
- Также ответ можно представить в численной форме, используя вместо
-
1
Запишите преобразованную формулу. Если известна длина окружности круга, можно воспользоваться преобразованной формулой для вычисления его площади. Такая формула включает длину окружности, а не радиус, и записывается так:
-
2
Измерьте или запишите длину окружности. В некоторых ситуациях нельзя точно измерить диаметр или радиус. Если диаметр не нарисован или центр не отмечен, очень сложно найти точный центр круга. Длину окружности некоторых предметов (например, сковороды) довольно легко измерить с помощью рулетки, то есть можно найти более точное значение длины окружности, чем диаметра.[5]
- Например, длина окружности круга (или круглого предмета) равна 42 см.
-
3
-
4
Запишите формулу для вычисления площади круга. Запишите преобразованную формулу на основе соотношения между длиной окружности и радиусом. Подставьте последнее равенство в стандартную формулу для вычисления площади круга:[7]
-
5
Воспользуйтесь преобразованной формулой, чтобы решить задачу. Теперь в формуле вместо радиуса присутствует длина окружности, поэтому можно вычислить площадь круга по известной длине окружности. Подставьте значение длины окружности и выполните вычисления следующим образом:[8]
-
6
Запишите ответ. Если длина окружности дана в виде числа, а не произведения числа и
, ответ можно записать с
в знаменателе. Или вместо числа Пи подставьте его приблизительное значение (3,14).[9]
Реклама
-
1
Запишите известные величины. В некоторых задачах дана площадь сектора круга, по которой нужно найти площадь всего круга. Внимательно прочитайте такую задачу; ее условие может выглядеть так: «Площадь сектора круга равна 15
см2. Найдите площадь всего круга».[10]
-
2
Запомните определение сектора. Сектор круга – это часть круга, которая ограничена дугой и двумя радиусами. Пространство между такими радиусами и дугой называется сектором.[11]
-
3
Измерьте центральный угол сектора. Воспользуйтесь транспортиром, чтобы измерить угол между двумя радиусами. Линейку (прямолинейную шкалу) совместите с одним из радиусов, причем центр линейки должен совпадать с центром круга. Затем найдите величину угла; для этого посмотрите на точку пересечения второго радиуса с угломерной шкалой.[12]
- Не перепутайте внутренний и внешний угол между двумя радиусами. В задаче должно быть указано, с каким углом работать. Помните, что сумма внутреннего и внешнего углов равна 360 градусов.
- Во многих задачах центральный угол дан, то есть измерять его не нужно. Например, в задаче может быть сказано: «Центральный угол сектора равен 45 градусов»; если это не так, измерьте центральный угол.
-
4
Используйте преобразованную формулу для вычисления площади круга. Если известны площадь сектора и его центральный угол, используйте следующую преобразованную формулу, чтобы найти площадь круга: [13]
-
5
-
6
Запишите ответ. В нашем примере сектор составлял одну восьмую полного круга. Поэтому площадь полного круга равна 120
см2. Так как площадь сектора дана с постоянной
, скорее всего, ответ тоже можно представить с этой постоянной.[15]
- Чтобы записать ответ в численной форме, умножьте 120 x 3,14 = 376,8 см2.
Реклама
Об этой статье
Эту страницу просматривали 264 354 раза.



![Rendered by QuickLaTeX.com [boxed {S= frac{pi d^2}{4}} eqno (2)]](https://repetitor-mathematics.ru/wp-content/ql-cache/quicklatex.com-5079fe338a2871a3e6bbc2cbdac83ab4_l3.png)
![Rendered by QuickLaTeX.com [boxed {S=frac{l^2}{4 pi}} eqno (3)]](https://repetitor-mathematics.ru/wp-content/ql-cache/quicklatex.com-622cc9e058f3b1ba7c9122cffdbec07d_l3.png)
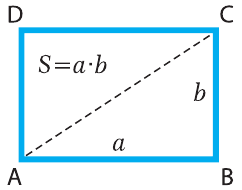
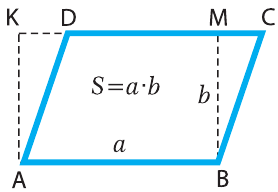
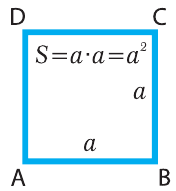
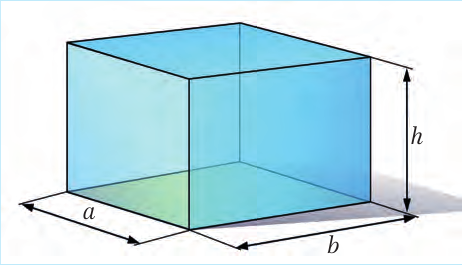
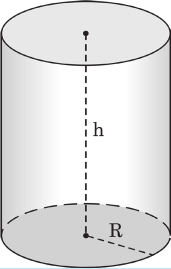
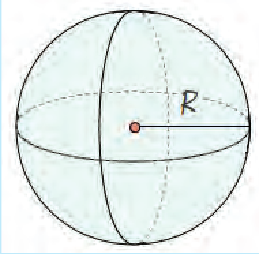 Рис. 6.6.
Рис. 6.6.