СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
1 мая
Новый сервис: можно исправить ошибки!
29 апреля
Разместили актуальные шкалы ЕГЭ — 2023
24 апреля
Учителю: обновленный классный журнал
7 апреля
Новый сервис: ссылка, чтобы записаться к учителю
30 марта
Решения досрочных ЕГЭ по математике
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий.
Круг и его элементы
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Задания Д4 № 26237 
i
На клетчатой бумаге с размером клетки 1 × 1 изображён вписанный в окружность угол ABC. Найдите его градусную величину.
Аналоги к заданию № 27890: 26237 27891 509571 Все
Решение
·
Видеокурс
·
Помощь
2
Задания Д4 № 27562
i
На клетчатой бумаге с размером клетки
изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
Аналоги к заданию № 27562: 5297 5299 5301 … Все
Решение
·
1 комментарий
·
Видеокурс
·
Помощь
3
Задания Д4 № 27946
i
На клетчатой бумаге с размером клетки 1
1 изображён прямоугольный треугольник. Найдите радиус окружности, описанной около этого треугольника.
Решение
·
Видеокурс
·
Помощь
4
Задания Д4 № 245008
i
На клетчатой бумаге с размером клетки 1 см
1 см изображено кольцо. Найдите его площадь. В ответ запишите площадь, делённую на 
Ответ дайте в квадратных сантиметрах.
Аналоги к заданию № 245008: 263421 263419 263479 … Все
Решение
·
Видеокурс
·
Помощь
5
Задания Д4 № 250883
i
На клетчатой бумаге с размером клетки
изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
Аналоги к заданию № 250883: 250903 Все
Решение
·
Видеокурс
·
Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
На клетчатой бумаге нарисованы два круга
Здравствуйте, друзья! В состав ЕГЭ по математике входят задачи связанные с нахождением площади круга или его частей (сектора, кольцевых элементов). Фигура задаётся на листе в клетку. В одних задачах масштаб клетки задаётся 1×1 сантиметр, в других он не оговаривается – даётся площадь элемента круга или самого круга.
Задания неглубокие, необходимо помнить формулу площади круга, уметь визуально (по клеткам) определить радиус круга, какую долю от круга составляет выделенный сектор. Кстати, на блоге имеется статья о площади сектора. Её содержание к решению представленных ниже задач отношения не имеет, но для тех, кто хочет вспомнить формулу площади круга и площади сектора будет весьма полезна. Рассмотрим задачи (взяты из открытого банка заданий):
Найдите (в см 2 ) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см. В ответе запишите S/л.
Для того, чтобы площадь фигуры (кольца) необходимо из площади круга радиусом равным 2 вычесть площадь круга с радиусом 1. Формула площади круга:
Разделим результат на число Пи и запишем ответ.
На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 51. Найдите площадь заштрихованной фигуры.
Площадь заштрихованной фигуры можно найти вычислив разность между площадью большего круга и площадью меньшего. Определим во сколько раз площадь большего отличается от площади меньшего. Пусть радиус меньшего равен R, тогда его площадь равна:
Радиус большего круга в два раза больше (видно по клеткам). Значит, его площадь равна:
Получили, что его площадь в 4 раза больше.
Следовательно, она равна 51∙4 = 204 см 2
Таким образом, площадь заштрихованной фигуры равна 204 – 51 = 153 см 2 .
*Второй способ. Можно было вычислить радиус малого круга, затем определить радиус большего. Далее найти площадь большего и вычислить площадь искомой фигуры.
На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 1. Найдите площадь заштрихованной фигуры.
Данная задача по ходу решения практически не отличается от предыдущей, разница состоит лишь в том, что круги имеют разные центры.
Несмотря на то, что видно, что радиус большего круга в 2 раза больше радиуса меньшего, советую вам обозначить размер клетки переменной х (икс).
Так же, как и в предыдущей задаче, определим во сколько раз площадь большего отличается от площади меньшего. Выразим площадь меньшего круга, так как его радиус равен 3х:
Выразим площадь большего круга, так как его радиус равен 6х:
Как видно, площадь большего круга в 4 раза больше.
Следовательно, она равна 1∙4 = 4 см 2
Таким образом, площадь заштрихованной фигуры равна 4 – 1 = 3 см 2 .
На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 9. Найдите площадь заштрихованной фигуры.
Обозначим размер клетки переменной х (икс).
Определим во сколько раз площадь большего круга отличается от площади меньшего. Выразим площадь меньшего круга. Так как его радиус равен 3 ∙ х, то
Выразим площадь большего круга. Так как его радиус равен 4 ∙ х, то
Разделим площадь большего на площадь меньшего:
То есть, площадь большего круга в 16/9 раза больше площади меньшего, следовательно, она равна:
Таким образом, площадь заштрихованной фигуры равна 16 – 9 = 7 см 2 .
Вычислим радиус меньшего круга. Его площадь равна 9, значит,
Найдём размер клетки и затем сможем определить радиус большего круга. Размер клетки равен:
Так как радиус большего круга соответствует 4 клеткам, то его радиус будет равен:
Определяем площадь большего круга:
Находим разность: 16 – 9 = 7 см 2
На клетчатой бумаге нарисован круг площадью 48. Найдите площадь заштрихованного сектора.
В этой задаче очевидно, что заштрихованная часть составляет половину от площади всего круга, то есть равна 24.
На клетчатой бумаге изображён круг. Какова площадь круга, если площадь заштрихованного сектора равна 32?
По рисунку видно, что площадь сектора составляет треть от площади круга. Значит, площадь круга будет равна 32∙3 = 96.
Найдите (в см 2 ) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см. В ответе запишите S/л.
Найдите площадь S круга, считая стороны квадратных клеток равными 1. В ответе укажите S/л.
В задачах связанных с площадью сектора круга необходимо уметь определять какую долю он составляет от площади круга. Это сделать не сложно, так как в подобных задачах центральный угол сектора кратен 30 либо 45.
В задачах связанных с нахождением площадей кольцевых элементов есть разные пути для решения, оба показаны в решённых заданиях. Способ, в котором размер клетки обозначается через переменную х, и затем определяются радиусы более универсален.
Но самое главное – не запоминать эти способы. Можно найти и третий и четвёртый путь решения. Главное – это знать формулу площади круга и уметь логически рассуждать.
На этом всё. Успеха вам!
С уважением, автор проекта Александр Крутицких.
Как найти площадь окружности на клетчатой бумаге 1х1
На клетчатой бумаге с размером клетки 1 × 1 изображён вписанный в окружность угол ABC. Найдите его градусную величину.
Аналоги к заданию № 27890: 26237 27891 509571 Все
На клетчатой бумаге с размером клетки изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
Отрежем от закрашенной фигуры сектор, отмеченный синим цветом, и добавим к ней сектор, выделенный красным цветом. Указанные секторы равны, поэтому площадь фигуры не изменилась. Следовательно, она равна трём четвертям площади круга, радиус которого см. Поэтому
см 2 .
Хотелось бы более “научного” доказательства. Аргумент “это видно” не достаточен, так как всем видно разное. Спасибо!
На рисунке ВИДНО, что они равны. Или задайте прямые уравнениями и и найдите угол между ними. Но то, что уравнения именно такие, тоже ВИДНО по рисунку. Задания на работу с рисунками предполагают считывание информации с рисунка.
На клетчатой бумаге с размером клетки 1 1 изображён прямоугольный треугольник. Найдите радиус окружности, описанной около этого треугольника.
Треугольник прямоугольный, значит, радиус описанной вокруг него окружности равен половине гипотенузы.
Круг на клетчатой бумаге
Рассмотрим задачи, в которых изображён круг на клетчатой бумаге и требуется по известной площади круга найти площадь заштрихованного сектора либо найти площадь круга по данному значению площади сектора.
Для решения обеих задач надо определить величину соответствующего ему центрального угла.
Градусная мера окружности — 360°. Зная центральный угол, найдем, какую часть площадь закрашенного сектора составляет от площади круга.
Самые простые задания этого вида — те, в которых центральный угол — прямой. 90° составляют четверть от 360°. Отсюда, для нахождения площади сектора площадь круга следует разделить на 4. И наоборот, для нахождения площади круга по известной площади сектора площадь сектора умножаем на 4.
Стороны прямого угла, чаще всего, либо проведены по клеточкам (одна сторона — горизонтально, другая — вертикально), либо делят каждую клеточку по диагонали (как диагональ квадрата).
Определить прямой угол можно даже с помощью листа бумаги (приложив его к центру круга).
1) На клетчатой бумаге изображён круг площадью 60.
Найти площадь заштрихованного сектора.
Так как центральный угол, соответствующий данному сектору, равен 90º, то
2) На клетчатой бумаге изображён круг.
Какова площадь круга, если площадь заштрихованного сектора равна 17?
Так как стороны угла делят каждую клеточку по диагонали, образуя с горизонтальной прямой, проходящей из вершины угла, углы по 45°, то центральный угол равен 90º.
Следовательно, площадь сектора составляет 1/4 от площади круга: Sкруга=Sсектора:(1/4)=17·4=68.
3) Найти площадь круга, если площадь заштрихованного сектора равна 21.
Площадь заштрихованного сектора составляет 3/4 площади круга.
Следовательно, чтобы найти площадь круга, надо площадь сектора разделить на 3/4:
4) Какова площадь круга если известно, что площадь закрашенного сектора равна 11?
Соответствующий центральный угол равен 45° (одно сторона угла проведена по горизонтали, другая делит каждую клеточку по диагонали (является диагональю квадрата).
Так как 45° составляет от 360° 1/8 часть, то
5) На клетчатой бумаге изображен круг площадью 96.
Найдите площадь заштрихованного сектора.
Центральный угол, соответствующий незакрашенной части, равен 45°, то есть составляет 1/8 площади круга.
Sзакрашенного сектора=Sнезакрашенного сектора-Sкруга=96-12=84.
А как определить на клетчатой бумаге центральные углы в 60° и 30°?
Можно рассуждать следующим образом.
Рассмотрим треугольник ABC.
Так как BH — его высота и медиана, то ABC — равнобедренный с основанием AO. Значит, AB=BO.
Но AO=BO (как радиусы).
Следовательно, AB=BO=AO, то есть треугольник ABC — равносторонний. Следовательно, все его углы равны по 60°, в частности, ∠AOB=60°.
6) Найти площадь заштрихованного сектора, если площадь круга равна 30.
Соответствующий центральный угол равен 60°. Значит, площадь сектора составляет 1/6 от площади круга и Sсектора=Sкруга:6=30:6=5.
7) Найти площадь круга, если площадь заштрихованного сектора равна 24.
Так как центральный угол заштрихованного сектора равен 30°, то площадь сектора составляет 1/12 часть от площади круга.
8) Найти площадь круга, изображенного на клетчатой бумаге, если площадь заштрихованного сектора равна 60.
Центральный угол, соответствующий незакрашенному сектору, равен 60°. Значит, площадь незакрашенной части составляет 1/6 площади круга.
Следовательно, на площадь закрашенной части приходится 5/6 круга:
В некоторых случаях центральный угол можно найти как сумму или разность других центральных углов.
9) Центральный угол равен 30+45=75°,
площадь заштрихованного сектора составляет
1/12+1/8=5/24 площади круга, то есть
10) Центральный угол равен 180-30=150°,
площадь заштрихованного сектора составляет 1/2-1/12=5/12 площади круга,
11) Центральный угол равен 60-45=15°,
площадь заштрихованного сектора составляет 1/24 площади круга
12) Центральный угол равен 15+90=105°
[spoiler title=”источники:”]
http://ege.sdamgia.ru/test?theme=123
[/spoiler]
Рассмотрим задачи, в которых изображён круг на клетчатой бумаге и требуется по известной площади круга найти площадь заштрихованного сектора либо найти площадь круга по данному значению площади сектора.
Для решения обеих задач надо определить величину соответствующего ему центрального угла.
Градусная мера окружности — 360°. Зная центральный угол, найдем, какую часть площадь закрашенного сектора составляет от площади круга.
Самые простые задания этого вида — те, в которых центральный угол — прямой. 90° составляют четверть от 360°. Отсюда, для нахождения площади сектора площадь круга следует разделить на 4. И наоборот, для нахождения площади круга по известной площади сектора площадь сектора умножаем на 4.
Стороны прямого угла, чаще всего, либо проведены по клеточкам (одна сторона — горизонтально, другая — вертикально), либо делят каждую клеточку по диагонали (как диагональ квадрата).
Определить прямой угол можно даже с помощью листа бумаги (приложив его к центру круга).
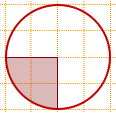
1) На клетчатой бумаге изображён круг площадью 60.
Найти площадь заштрихованного сектора.
Решение:
Так как центральный угол, соответствующий данному сектору, равен 90º, то
Sсектора=Sкруга:4=60:4=15.
Обратная задача.
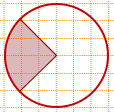2) На клетчатой бумаге изображён круг.
Какова площадь круга, если площадь заштрихованного сектора равна 17?
Решение:
Так как стороны угла делят каждую клеточку по диагонали, образуя с горизонтальной прямой, проходящей из вершины угла, углы по 45°, то центральный угол равен 90º.
Следовательно, площадь сектора составляет 1/4 от площади круга: Sкруга=Sсектора:(1/4)=17·4=68.
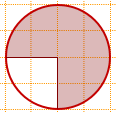3) Найти площадь круга, если площадь заштрихованного сектора равна 21.
Решение:
Площадь заштрихованного сектора составляет 3/4 площади круга.
Следовательно, чтобы найти площадь круга, надо площадь сектора разделить на 3/4:
Sкруга=Sсектора:(3/4)=21: (3/4)=21·4:3=28.
4) Какова площадь круга если известно, что площадь закрашенного сектора равна 11?
Решение:
Соответствующий центральный угол равен 45° (одно сторона угла проведена по горизонтали, другая делит каждую клеточку по диагонали (является диагональю квадрата).
Так как 45° составляет от 360° 1/8 часть, то
Sкруга=Sсектора:(1/8)=11: (1/8)=11·8=88.
5) На клетчатой бумаге изображен круг площадью 96.
Найдите площадь заштрихованного сектора.
Решение:
Центральный угол, соответствующий незакрашенной части, равен 45°, то есть составляет 1/8 площади круга.
Sнезакрашенного сектора=Sкруга:8=96:8=12.
Sзакрашенного сектора=Sнезакрашенного сектора-Sкруга=96-12=84.
А как определить на клетчатой бумаге центральные углы в 60° и 30°?
Можно рассуждать следующим образом.
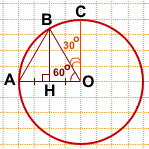Рассмотрим треугольник ABC.
Так как BH — его высота и медиана, то ABC — равнобедренный с основанием AO. Значит, AB=BO.
Но AO=BO (как радиусы).
Следовательно, AB=BO=AO, то есть треугольник ABC — равносторонний. Следовательно, все его углы равны по 60°, в частности, ∠AOB=60°.
∠BOC=∠AOC-∠AOB=90°-60°=30°.
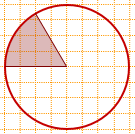6) Найти площадь заштрихованного сектора, если площадь круга равна 30.
Решение:
Соответствующий центральный угол равен 60°. Значит, площадь сектора составляет 1/6 от площади круга и Sсектора=Sкруга:6=30:6=5.
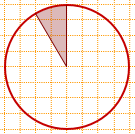7) Найти площадь круга, если площадь заштрихованного сектора равна 24.
Решение:
Так как центральный угол заштрихованного сектора равен 30°, то площадь сектора составляет 1/12 часть от площади круга.
Sкруга=Sсектора:(1/12)=24: (1/12)=24·12=288.
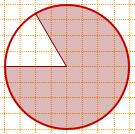8) Найти площадь круга, изображенного на клетчатой бумаге, если площадь заштрихованного сектора равна 60.
Решение:
Центральный угол, соответствующий незакрашенному сектору, равен 60°. Значит, площадь незакрашенной части составляет 1/6 площади круга.
Следовательно, на площадь закрашенной части приходится 5/6 круга:
Sкруга=Sсектора:(5/6)=60: (5/6)=60·6:5=72°.
В некоторых случаях центральный угол можно найти как сумму или разность других центральных углов.
9) 
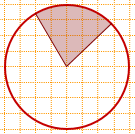Центральный угол равен 30+45=75°,
площадь заштрихованного сектора составляет
1/12+1/8=5/24 площади круга, то есть
Sсектора=Sкруга·(5/24)=Sкруга:24·5,
Sкруга=Sсектора:(5/24)=Sкруга: 5·24.
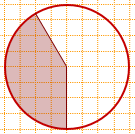10) Центральный угол равен 180-30=150°,
площадь заштрихованного сектора составляет 1/2-1/12=5/12 площади круга,
Sсектора=Sкруга·(5/12),
Sкруга=Sсектора:(5/12).
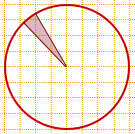11) Центральный угол равен 60-45=15°,
площадь заштрихованного сектора составляет 1/24 площади круга
и т.д.
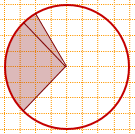12) Центральный угол равен 15+90=105°
(либо 180-30-45=105°),
площадь заштрихованного сектора составляет
1/24+1/4=7/24 и т.д.
Задачи на клетчатой бумаге интересны тем, что можно их решать различными способами – и через дополнительное построение, и через различные геометрические формулы. Так как задач таких сейчас полно в сети, ещё раз обозначу себе картинкой условие:
У нас нет ничего в условии кроме длины клетки, равной 1/√π
Как найти площадь?
Например, по такой формуле, где альфа – размер угла.
Но у нас нет ни угла, ни радиуса.
Значит, находим радиус. На глаз тут 4,5 клетки, но мы будем точнее, если нарисуем вот такой треугольник прямоугольник, в котором радиус будет гипотенузой и через теорему Пифагора его найдём.
(4/√π)2 + (2/√π)2 = 16/π+4/π = √(20/π)
Как найти угол? Если разделить всю окружность на 4 части, то видно, что закрашенная часть составит целую четверть и ещё её половинку. То бишь, 1/4+0,5Х1/4 Это не что иное как 3/8
Теперь считаем угол: 360Х3/8=135 градусов.
Теперь, когда у нас есть все данные, подставляем в формулу.
S=135/360 Х π Х (√(20/π))2
Квадрат и корень квадратный сокращаются, получаем 135/360 Х π Х 20/π
Следом сокращается и п, остаётся 135/360 Х 20/1 = 135/18 = 7,5
Поскольку площадь измеряется в квадратных сантиметрах в нашей задаче, то и ответ будет 7,5 кв.см
В 18 задании необходимо найти какую-либо часть фигуры, нарисованной на клетчатой бумаге. Именно клетчатая бумага 1×1 является особенностью данного задания. Задание не сложное, необходимо внимательно посчитать количество клеток и при необходимости выполнить действие. Опять же нам понадобятся элементарные знания геометрии для успешного решения данного задания. Ниже я разобрал типичные задания.
На клетчатой бумаге размером 1×1 изображён ромб. Найдите длину его большей диагонали.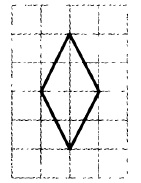
Внимательно смотрим на рисунок и видим, что длина одной диагонали ромба равна 2, а второй 4. Так как нас спрашивают длину большей диагонали, то в ответе нужно указать 4.
Ответ: 4
pазбирался: Даниил Романович | обсудить разбор | оценить
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии.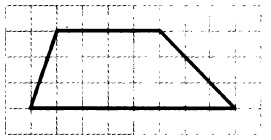
Мы знаем, что средняя линия равна полусумме оснований. Нижнее основание данной трапеции равно 8 клеткам, а верхнее – 4 клеткам. Полусумма оснований:
( 8 + 4 ) / 2 = 6
Ответ: 6
pазбирался: Даниил Романович | обсудить разбор | оценить
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.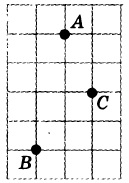
Проведем необходимые отрезки:
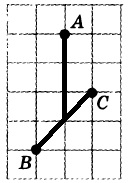
Из рисунка можно вычислить длину – это 3.
Ответ: 3
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите тангенс острого угла, изображённого на рисунке.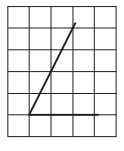
Детализируем рисунок. Проведем вертикальную линию, которая отсекает от сторон угла 2 клетки по горизонтали . В результате получен прямоугольный ∆АВС:
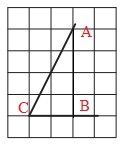
Чтобы получить ответ на вопрос задачи, требуется найти tg∠C.
Согласно определению тангенса, из треугольника ∆АВС можем записать:
tg∠C=AB/BC.
По рисунку подсчитываем длины отрезков АВ и ВС (по кол-ву клеток):
АВ=4, ВС=2.
Получаем:
tg∠C=4/2=2.
Ответ: 2
pазбирался: Даниил Романович | обсудить разбор | оценить
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.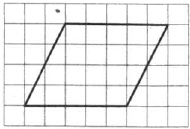
Площадь параллелограмма вычисляется так:
S=a·ha
Обозначим a и ha на рисунке:
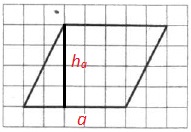
Теперь определим их длины по рисунку:
a=5; ha=4.
Вычисляем искомую площадь:
S=5·4=20.
Ответ: 20
pазбирался: Даниил Романович | обсудить разбор | оценить
На клетчатой бумаге с размером клетки 1×1 изображен ромб. Найдите площадь этого ромба.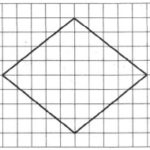
Площадь ромба будем искать через его диагонали:
S=d1·d2/2
Линии диагоналей обозначим на рисунке красным:
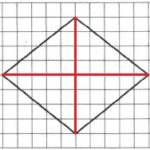
Обозначим меньшую диагональ через d1, большую – через d2 (можно наоборот). Определим их длины из рисунка:
d1=8; d2=10.
Находим площадь фигуры:
S=8·10/2=40
Ответ: 40
pазбирался: Даниил Романович | обсудить разбор | оценить
На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.
Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.
Ответ: 4
pазбирался: Даниил Романович | обсудить разбор | оценить
- ОГЭ по математике
Вебинар на тему: «Задания по геометрии в ОГЭ-2021 по математике»
Ведущая: Фридман Елена Михайловна
→ презентация к вебинару
Рассмотрены задания из ОГЭ по геометрии:
— Планиметрия. Часть 1 (задания 15 – 18);
— Задание 25 из части 2.
| № | Понятия и свойства |
| 15 | Треугольник. Медиана, высота, биссектриса, средняя линия, сумма углов, внешний угол, соотношения между сторонами и углами. Теорема косинусов. Четырехугольник. Параллелограмм (ромб, прямоугольник, квадрат), трапеция, их свойства. Признаки параллельности прямых. |
| 16 | Вписанные и описанные треугольники и четырехугольники. Касательные, хорды, углы, секущая, угол, образованный касательной и хордой, вписанный угол. Теорема синусов. |
| 17 | Площадь треугольника, четырехугольника, решение треугольника. |
| 18 | Задачи на клетчатой бумаге, площадь фигуры, центральный и вписанный углы, градусная мера дуги окружности |
| 19 | Выбор верного утверждения |
Примеры задач 25:
Связанные страницы:
Решение заданий Варианта №18 из сборника ОГЭ 2022 по математике И.В. Ященко 36 типовых вариантов ФИПИ школе. ГДЗ решебник для 9 класса. Ответы с решением. Полный разбор всех заданий.
ЧАСТЬ 1
Задание 1-5.
Сергей Петрович решил построить на дачном участке теплицу длиной 4 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Сергей Петрович заказал металлические дуги в форме полуокружностей длиной 5 м каждая и покрытие для обтяжки.
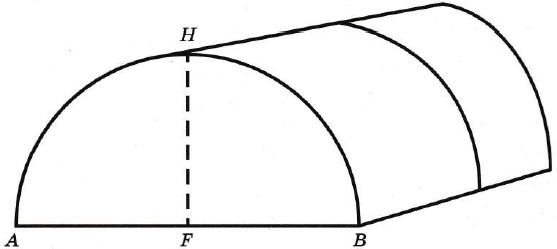
Отдельно требуется купить плёнку для передней и задней стенок теплицы. Внутри теплицы Сергей Петрович планирует сделать три грядки по длине теплицы – одну центральную широкую грядку и две узкие грядки по краям. Между грядками будут дорожки шириной 40 см, для которых необходимо купить тротуарную плитку размером 20 см х 20 см. Высота теплицы показана на рисунке отрезком HF.
Задание 6.
Найдите значение выражения frac{1}{frac{1}{21}+frac{1}{28}}.
Задание 7.
На координатной прямой отмечены числа х, у и z.
Какая из разностей у – z, у – x, x – z отрицательна?
1) у – z
2) у – x
3) x – z
4) ни одна из них
Задание 8.
Найдите значение выражения frac{2^{-6}cdot 2^{6}}{2^{-8}}.
Задание 9.
Решите уравнение х2 – 35 = 2х.
Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Задание 10.
Вероятность того, что новый утюг прослужит больше года, равна 0,94. Вероятность того, что он прослужит больше двух лет, равна 0,85. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Задание 11.
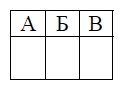
На рисунках изображены графики функций вида у = ах2 + bх + c. Установите соответствие между графиками функций и знаками коэффициентов а и с.
ГРАФИКИ
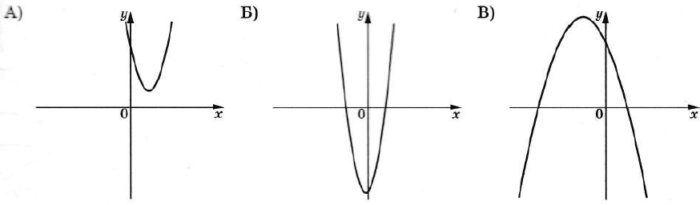
КОЭФФИЦИЕНТЫ
1) а > 0‚ с < 0
2) а < 0, с > 0
3) а > 0, с > 0
В таблице под каждой буквой укажите соответствующий номер.
Задание 12.
Работа постоянного тока (в джоулях) вычисляется по формуле A = I2Rt‚ где I – сила тока (в амперах), R – сопротивление (в омах), t – время (в секундах). Пользуясь этой формулой, найдите А (в джоулях), если t = 10 с, I = 4 A и R = 2 Ом.
Ответ задания: 320.
Задание 13.
Укажите решение неравенства
– 3 – x ≤ 4x + 7
1) (–∞; –0,8]
2) [–2; +∞)
3) (–∞; –2)
4) (–0,8; +∞)
Задание 14.
В 8:00 часы сломались и за каждый следующий час отставали на одно и то же количество минут по сравнению с предыдущим часом. В 23:00 того же дня часы отставали на 15 минут. На сколько минут отставали часы спустя 36 часа после того, как они сломались?
Ответ задания: 36.
Задание 15.
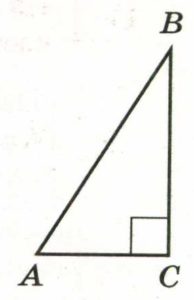
В треугольнике АВС угол С равен 90°‚ АС = 14‚ АВ = 20. Найдите sin В.
Задание 16.
В окружности с центром О отрезки АС и BD – диаметры. Угол AOD равен 108°. Найдите угол АСВ. Ответ дайте в градусах.
Задание 17.
Площадь параллелограмма АВСD равна 96. Точка Е – середина стороны АВ. Найдите площадь треугольника СВЕ.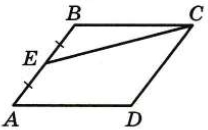
Задание 18.
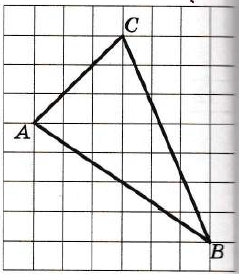
На клетчатой бумаге с размером клетки 1 x 1 изображён треугольник АВС. Найдите длину его медианы, проведённой из вершины С.
Задание 19.
Какие из следующих утверждений верны?
1) Если диагонали параллелограмма равны, то он является ромбом.
2) Сумма острых углов прямоугольного треугольника равна 90 градусам.
3) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
ЧАСТЬ 2
Задание 20.
Решите уравнение х4 = (3х – 4)2.
Задание 21.
Моторная лодка прошла против течения реки 208 км и вернулась в пункт отправления, затратив на обратный путь на 5 часов меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 5 км/ч.
Ответ задания: 21.
Задание 22.
Постройте график функции y = x2 – 11x – 2|x – 5| + 30 и определите, при каких значениях m прямая у = m имеет с графиком ровно три общие точки.
Ответ задания: –0,25; 0.
Задание 23.
Прямая пересекает стороны АВ и ВС треугольника АВС в точках К и N соответственно. Известно, что АВ = 9, ВС = 12, АС = 18, АК = 5, СN = 9. Найдите длину отрезка КN.
Ответ задания: 6.
Задание 24.
Сторона АD параллелограмма АВСD вдвое больше стороны АВ. Точка G – середина стороны АD. Докажите, что BG – биссектриса угла АBС.
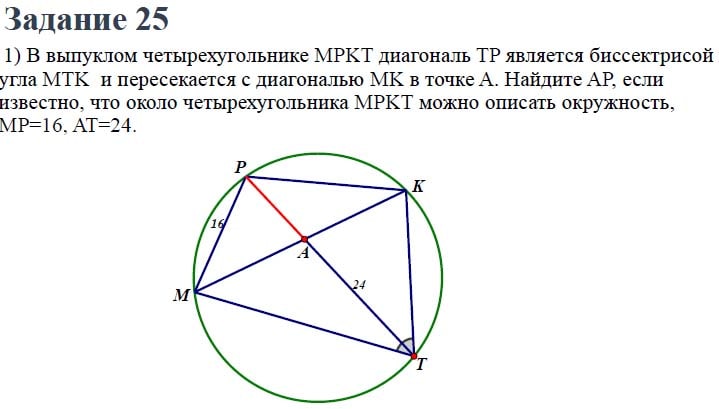
Задание 25.
В трапеции АВСD основания АD и ВС равны соответственно 34 и 2, а сумма углов при основании АD равна 90°. Найдите радиус окружности, проходящей через точки А и В и касающейся прямой СD, если АВ = 24.
Ответ задания: 13,5.
Источник варианта: Сборник ОГЭ 2022 по математике. Типовые экзаменационные варианты. 36 вариантов. Под редакцией И.В. Ященко.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 3.7 / 5. Количество оценок: 3
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил.
Слайд 2
Текст слайда:
Задания:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Демо-версия!
Слайд 3
Текст слайда:
№1
Найдите синус угла АОВ. В ответе укажите
значение синуса, умноженное на
17
Ответ
В
А
О
Алгоритм (3):
3. Выполнить вычисления и записать ответ .
1. Вспомнить что называют синусом острого угла прямоугольного треугольника.
2. Записать формулу нахождения sinО.
Построение:
С
4
4
Слайд 4
Текст слайда:
№2
KarMaN01@yandex.ru
Информация
Слайд 5
Текст слайда:
№3
KarMaN01@yandex.ru
Информация
Слайд 6
Текст слайда:
№4
KarMaN01@yandex.ru
Информация
Слайд 7
Текст слайда:
№5
KarMaN01@yandex.ru
Информация
Слайд 8
Текст слайда:
№6
KarMaN01@yandex.ru
Информация
Слайд 9
Текст слайда:
№7
KarMaN01@yandex.ru
Информация
Слайд 10
Текст слайда:
№8
KarMaN01@yandex.ru
Информация
Слайд 11
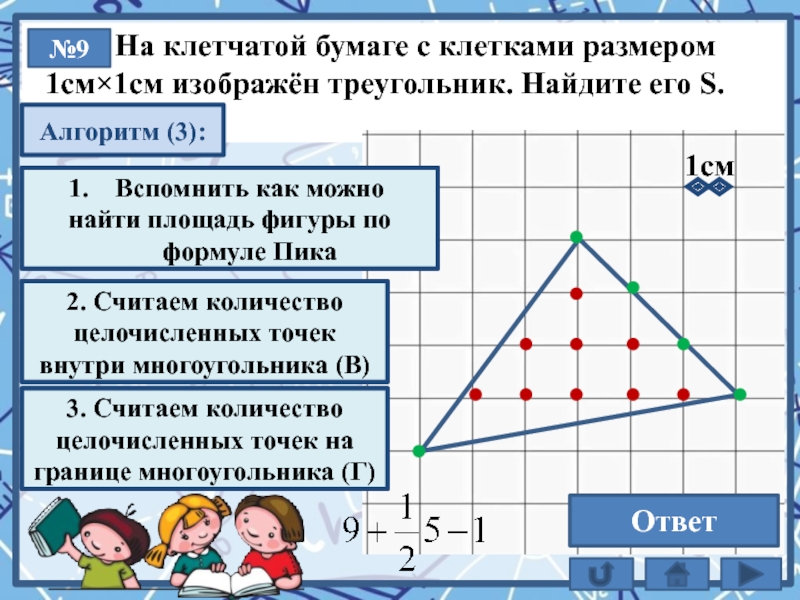
Текст слайда:
На клетчатой бумаге с клетками размером
1см×1см изображён треугольник. Найдите его S.
№9
10,5
Ответ
Алгоритм (3):
Площадь многоугоугольника с целочисленными вершинами равна сумме В + Г/2 – 1
Вспомнить как можно
найти площадь фигуры по формуле Пика
2. Считаем количество целочисленных точек внутри многоугольника (В)
1cм
3. Считаем количество целочисленных точек на границе многоугольника (Г)
Слайд 12
Текст слайда:
№10
KarMaN01@yandex.ru
Информация
Слайд 13
Текст слайда:
На клетчатой бумаге с клетками размером 1см×1см
изображён параллелограмм. Найдите его высоту,
опущенную на большую сторону.
№11
4
Ответ
Алгоритм (3):
3. Сравнить стороны и записать ответ к задаче.
1. Высота параллелограмма – перпендикуляр из вершины к противоположной стороне.
Вспомнить что называют высотой параллелограмма.
2. Провести высоты и из тр-ка АВН определить
сторону АВ
4
6
1cм
В
А
Н
Слайд 14
Текст слайда:
№12
KarMaN01@yandex.ru
Информация
Слайд 15
Текст слайда:
№13
KarMaN01@yandex.ru
Информация
Слайд 16
Текст слайда:
№14
KarMaN01@yandex.ru
Информация
Слайд 17
Текст слайда:
№15
KarMaN01@yandex.ru
Информация
Слайд 18
Текст слайда:
№16
KarMaN01@yandex.ru
Информация
Слайд 19
Текст слайда:
№17
KarMaN01@yandex.ru
Информация
Слайд 20
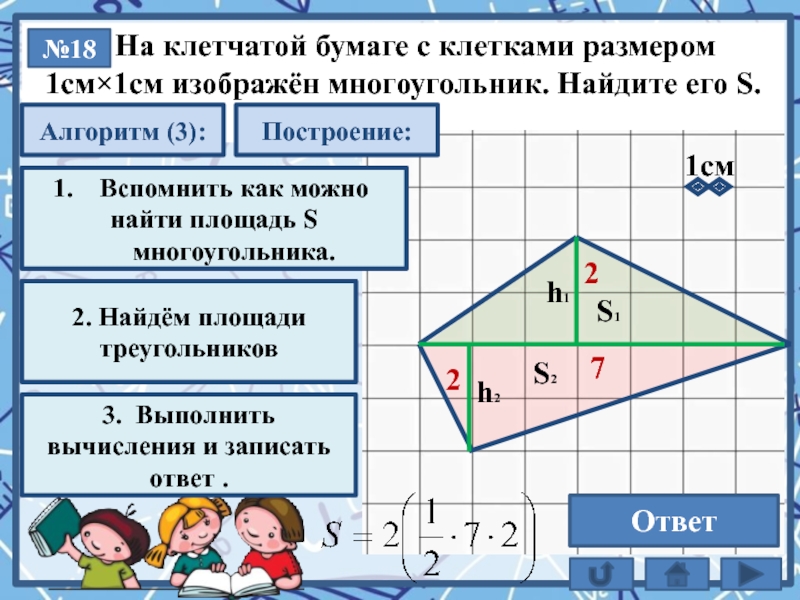
Текст слайда:
На клетчатой бумаге с клетками размером
1см×1см изображён многоугольник. Найдите его S.
№18
14
Ответ
S1
Алгоритм (3):
3. Выполнить вычисления и записать ответ .
1. Площадь многоугольника равна сумме площадей фигур из которых состоит (S1 + S2)
Вспомнить как можно
найти площадь S многоугольника.
2. Найдём площади треугольников
Построение:
h1
2
7
1cм
S2
2
h2
Слайд 21
Текст слайда:
№19
KarMaN01@yandex.ru
Информация
Слайд 22
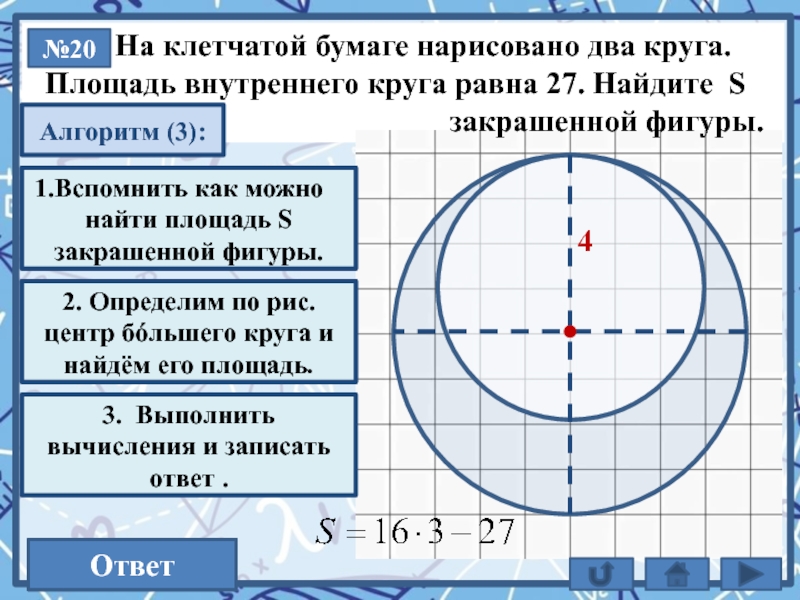
Текст слайда:
На клетчатой бумаге нарисовано два круга.
Площадь внутреннего круга равна 27. Найдите S
закрашенной фигуры.
№20
Алгоритм (3):
3. Выполнить вычисления и записать ответ .
S = Sб – Sм
Вспомнить как можно
найти площадь S закрашенной фигуры.
2. Определим по рис. центр бóльшего круга и найдём его площадь.
4
21
Ответ
Слайд 23
Текст слайда:
Уважаемые пользователи, дорогие коллеги!
Если Вам понравился ресурс, то получить полную версию
Вы можете, написав мне на электронную почту:
Пожалуйста, в письме указывайте ФИО
Описание:
Презентация состоит из 24 рабочих слайдов
В ресурсе представлено 20 задач по заявленной теме
с подробным разбором решения.
Задачи соответствуют спецификации и кодификатору к демонстрационному варианту КИМ-2020 по математике, представленного на сайте ФИПИ
Предлагаю подробный разбор заданий №8 и №10
Спасибо за интерес к работе.
Желаю Вам интересных уроков и успешных учеников!
С уважением, КарМаН
KarMaN01@yandex.ru
Слайд 24
Текст слайда:
Титульный слайд
Фон слайдов
источники
Дети в классе
Презентация на тему Задание №18 ОГЭ математика 2021 с решениями, из раздела: Образование. Эта презентация содержит 27 слайда(ов). Информативные слайды и изображения помогут Вам заинтересовать аудиторию. Скачать конспект-презентацию на данную тему можно внизу страницы, поделившись ссылкой с помощью социальных кнопок. Также можно добавить наш сайт презентаций в закладки! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них. Все права принадлежат авторам презентаций.
Слайды и текст этой презентации
Открыть в PDF
Слайд 2
Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 отмечены три точки А, В и С. Найдите расстояние от точки А до прямой ВС.
ЗАДАЧА №1
Слайд 3
Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 отмечены три точки А, В и С. Найдите расстояние от точки А до прямой ВС.
ЗАДАЧА №1
ОТВЕТ: 3.
Слайд 4
Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображен ромб. Найдите длину его большей диагонали.
ЗАДАЧА №2
Слайд 5
Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображен ромб. Найдите длину его большей диагонали.
ЗАДАЧА №2
ОТВЕТ: 10.
Слайд 6
Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 отмечены три точки А, В и С. Найдите расстояние от точки А до середины ВС.
ЗАДАЧА №3
Слайд 7
Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 отмечены три точки А, В и С. Найдите расстояние от точки А до середины ВС.
ЗАДАЧА №3
ОТВЕТ: 6.
Слайд 8
Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображен треугольник. Найдите его площадь.
ЗАДАЧА №4
Слайд 9
Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображен треугольник. Найдите его площадь.
ЗАДАЧА №4
ОТВЕТ: 21.
Слайд 10
Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображена трапеция. Найдите ее площадь.
ЗАДАЧА №5
Слайд 11
Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображена трапеция. Найдите ее площадь.
ЗАДАЧА №5
ОТВЕТ: 33.
Слайд 12
Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображена фигура. Найдите ее площадь.
ЗАДАЧА №6
Слайд 13
Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображена фигура. Найдите ее площадь.
ЗАДАЧА №6
ОТВЕТ: 26.
Слайд 14
Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображен параллелограмм. Найдите площадь этого параллелограмма.
ЗАДАЧА №7
Слайд 15
Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображен параллелограмм. Найдите площадь этого параллелограмма.
ЗАДАЧА №7
ОТВЕТ: 42.
Слайд 16
Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображен ромб. Найдите площадь ромба.
ЗАДАЧА №8
Слайд 17
Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображен ромб. Найдите площадь ромба.
ЗАДАЧА №8
ОТВЕТ: 20.
Слайд 18
Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображен треугольник. Найдите длину его средней линии, параллельной стороне АС.
ЗАДАЧА №9
Слайд 19
Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображен треугольник. Найдите длину его средней линии, параллельной стороне АС.
ЗАДАЧА №9
ОТВЕТ: 4,5.
Слайд 20
Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображена трапеция. Найдите длину ее средней линии.
ЗАДАЧА №10
Слайд 21
Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображена трапеция. Найдите длину ее средней линии.
ЗАДАЧА №10
ОТВЕТ: 5,5.
Слайд 22
Текст слайда:
Найти тангенс угла АОВ, изображенного на рисунке.
ЗАДАЧА №11
Слайд 23
Текст слайда:
Найти тангенс угла АОВ, изображенного на рисунке.
ЗАДАЧА №11
ОТВЕТ: 3,5.
Слайд 24
Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображен параллелограмм. Найдите площадь этого параллелограмма.
ЗАДАЧА №12
Слайд 25
Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображен параллелограмм. Найдите площадь этого параллелограмма.
ЗАДАЧА №12
ОТВЕТ: 14.
Слайд 26
Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображен треугольник. Найдите площадь этого треугольника.
ЗАДАЧА №13
Слайд 27
Текст слайда:
На клетчатой бумаге с размером клетки 1 x 1 изображен треугольник. Найдите площадь этого треугольника.
ЗАДАЧА №13
ОТВЕТ: 17,5.
