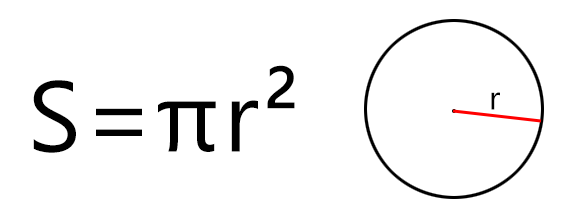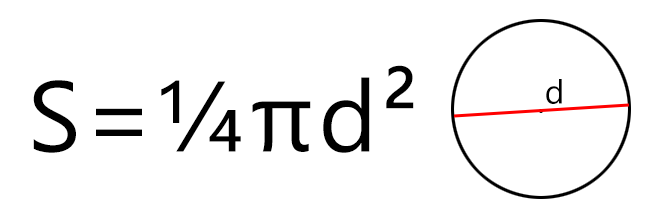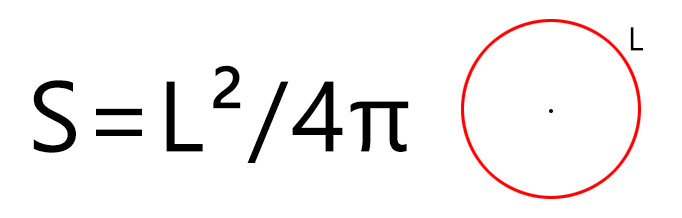Площадь круга через Диаметр
S – площадь круга,
d – диаметр круга,
π ≈ 3,141592653589
Площадь круга через Радиус
S – площадь круга,
r – радиус круга,
π ≈ 3,141592653589
Площадь круга через Длину Окружности
S – площадь круга,
l – длина окружности,
π ≈ 3,141592653589
Определения и термины
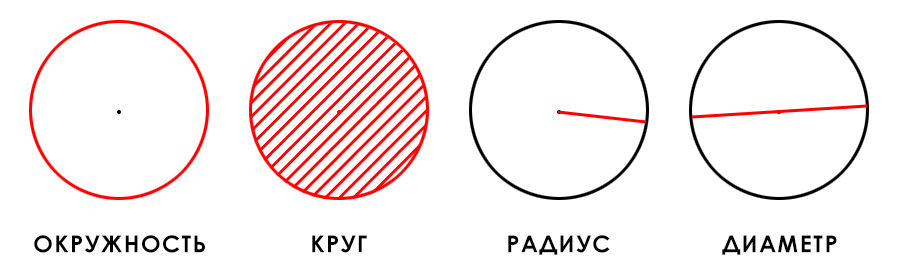
Круг – множество точек плоскости, расстояние до которых от данной точки (центра круга) не превышает заданного расстояния (радиуса круга).
Радиус круга – отрезок, соединяющий центр круга с любой точкой, которая лежит на внешней окружности круг
Диаметр круга – отрезок, соединяющий любые две точки, лежащие на внешней окружности круга, и проходящий через центр круга
Окружность – замкнутая плоская кривая состоящия из всех точек полскости равноудаленных от заданной точки (центра окружности)
Число Пи (π) – математическая константа, которая выражает отношение длины окружности к её диаметру.
Равно приблизительно 3,141592653589…
Площадь окружности
Окружность, по своей сути, является границей круга – замкнутой плоской кривой. Из определения следует, что площади окружности не существует,
а существует Площадь круга.
Как рассчитать площадь круга
На данной странице калькулятор поможет рассчитать площадь круга онлайн. Для расчета задайте радиус, диаметр или длину окружности.
Круг – множество точек плоскости, удаленных от заданной точки этой плоскости (центр круг) на расстояние, не превышающее заданное (радиус круга).
Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.
Через радиус
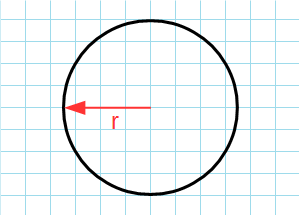
Формула для нахождения площади круга через радиус:
π – константа равная (3.14); r – радиус круга.
Через диаметр
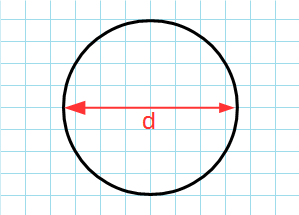
Формула для нахождения площади круга через диаметр:
π – константа равная (3.14); d – диаметр.
Через длину окружности

Формула для нахождения площади круга через длину окружности:
π – константа равная (3.14); l – длина окружности.
GELIOS
Высший разум
(512892)
12 лет назад
Как вычислить площадь ( S ) круга, зная только его диаметр (D)
Например, диаметр круга = 10 сантиметров.
То радиус ( R ). естественно будет равен 5 см. ( половину диаметра )
Есть ” пи ” = 3,14 – это математическая постоянная, выражающая отношение окружности к длине её диаметра.
Есть формула определения площади круга ( S ):
S круга = пи х R в квадрате.
Подставляем данные в формулу:
S круга = 3,14 х ( 5 х 5 ) = 3,14 х 25 см = 78,5 квадратных см.
Andrey Yaromenok
Ученик
(223)
6 лет назад
Как вычислить площадь ( S ) круга, зная только его диаметр (D)
Например, диаметр круга = 10 сантиметров.
То радиус ( R ). естественно будет равен 5 см. ( половину диаметра )
Есть ” пи ” = 3,14 – это математическая постоянная, выражающая отношение окружности к длине её диаметра.
Есть формула определения площади круга ( S ):
S круга = пи х R в квадрате.
Подставляем данные в формулу:
S круга = 3,14 х ( 5 х 5 ) = 3,14 х 25 см = 78,5 квадратных см.
бальзам
Ученик
(103)
5 лет назад
Что бы вычислить площадь круга, нужно:
– измерить длину круга 10 см. *3.14=31.4 см.
– поделить его длину на 4 равных отрезка 31.4 см: 4=7,85 см.
– мысленно собрать из этих отрезков квадрат и перемножить две его стороны. 7,85*2=15.7 кв/см.
Поиск площади круга – стандартная задача. Обычно, она задается школьникам в шестом классе, помогает мягко перейти к изучению более сложных примеров из тригонометрии.
В этом материале мы расскажем о том, как найти площадь круга с помощью формулы, обратим внимание на основные определения, отличия которых важно понимать учащемуся. Уже через непродолжительное время тренировок, вы сможете полностью освоить все методы решения задач и получать высокие оценки на уроке.
Важные определения
Прежде чем отвечать на вопрос о том, как найти площадь круга
по радиусу или диаметру по формуле, нужно установить основные определения. Мы
будем пользоваться следующими терминами:
- Круг. Так называют замкнутую плоскую кривую, в которой каждая точка имеет равное удаление от центральной.
- Окружность. Это сразу множество точек, которые располагаются на плоскости. При этом расстояние удаления от центра не будет превышать диаметр.
- Радиус. Расстояние от центра круга до любой его противоположной боковой точки.
- Диаметр. Полное расстояние от двух точек, расположенных на равном удалении друг от друга.
Как найти площадь
круга по диаметру: формула
Формула поиска площади для диаметра будет выглядеть так:
S = d2 : 4 × π.

Здесь:
- S – площадь.
- d – диаметр.
- π – константное число, которое в математических расчетах принимается как 3,14.
Как найти площадь
круга по радиусу: формула
Ищем итоговое значение также по формуле. Это S = π × r2. За число π берем константу 3,14. R – это радиус круга.
Как найти площадь через
длину окружности: формула
В математике иногда встречаются задачи, в которых известна длина окружности. В таком случае для решения нужно будет использовать стандартную формулу S = L2 : (4 × π).
Здесь L – это и есть площадь окружности.

Как ускорить процесс
обучения: советы специалистов
Есть несколько простых рекомендаций, которые помогают значительно ускорить учебный процесс, помогают быстрее освоиться с тем, как искать площадь круга по разным известным параметрам.
К ним относятся такие, как:
- Убедитесь в том, что ребенок хорошо понимает основные определения. Педагогическая практика показывает, что дети часто путают радиус и диаметр, что приводит к появлению ошибок и выставлению низких оценок учителями.
- В геометрии очень важна наглядность. Все задачи стоит решать исключительно вместе с рисунками круга на бумаге. Это также поможет ребенку значительно быстрее освоиться с использованием циркуля, линейки. Такие навыки сильно помогут в учебе в будущем.
- Не показывайте ученику своего непонимания предмета. Он всегда должен видеть в вас человека, который обладает уверенными знаниями по такому вопросу. Не стоит демотивировать его, рассказывать о бесполезности расчетов.
- Хорошее понимание предмета достигается исключительно через многократное решение задач. Их вы сможете без труда составить своими силами. Все что нужно – ставить условие поиска площади с разными исходными параметрами – длиной окружности, диаметром, радиусом и другими.
- Усложните задачи через введение разных параметров обозначения площади. Есть множество вариантов прописывания площади – это квадратные сантиметры, миллиметры, метры, дециметры и километры. Хорошей математической тренировкой станет перевод разных значений друг в друга. Также можно попробовать посчитать в гектарах. Все это помогает в таких предметах, как геометрия, тригонометрия и математика.
Почему важно
тренироваться в решении задач с площадью круга
Мы рассмотрели, как найти площадь круга по формуле. Осталось
только ответить на вопрос о том, почему понимание этого вопроса представляет
такое большое значение для школьника. Вот лишь несколько важных причин:
- Лучшее понимание геометрических терминов. Их
проще всего освоить на практике. Это пригодится при решении значительно более
сложных задач в старших классах. - Освоение единиц определения площади, решение
примеров по переводу величин друг в друга. Это поможет в геометрии и
математике. Можно воспользоваться умственным счетом или абакусом, что
дополнительно повысит успешность всего учебного процесса. - Создание базиса для решения комплексных
геометрических задач. Они часто направлены на то, чтобы ученик работал с
разными фигурами. При этом если пропустить понимание определения площади,
радиуса и диаметра круга, длины окружности, в будущем могут возникнуть
проблемы, отставание от программы.
Так как в школе дети часто не понимают таких сложных
предметов как геометрия до конца, рекомендуем уделить повышенное внимание
домашним занятиям. Это нужно делать регулярно и системно, но без сильного
давления на школьника, потенциально способного отбить интерес к учебе.
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Формула (формулы) площади круга
Найти площадь круга можно разными способами, в зависимости от известных данных.
По радиусу
Если дан только радиус, то площадь составит произведение константы Пи на квадрат радиуса. Расчёт будет по формуле (где r – радиус, а π – константа, равная 3,1415…):
Например, если радиус равен 2 метра, то площадь круг можно вычислить так S = 3,14 × 22 = 3,14 × 4 = 12,56 м2 (квадратных метров).
Через диаметр
Если известен диаметр, то площадь круга будет равняться одной четвёртой произведения Пи и квадрата диаметра. Формула площади круга будет такой (где d – диаметр, а π – константа, равная 3,1415…):
К примеру, если диаметр круга (площадь поверхности пиццы) составляет 35 сантиметров, то площадь такого круга будет равна S = ¼ × 3,14 × 352 = ¼ × 3,14 × 1225 = 962 см2 (квадратных сантиметра).
Через длину окружности
Если мы знаем только длину окружности (периметр круга), то рассчитать площадь фигуры можно по формуле (где L – длина окружности, а π – константа, равная 3,1415…):
Например, если длинна окружности составляет 120 мм, тогда площадь круга будет равна S = 1202 / (4 × 3,14) = 14 400 / (4 × 3,14) = 1146,5 мм2 (квадратных миллиметров).
Какие термины используются для поиска площади круга?
Для вычисления площади круга, в формулах были использованы следующие термины, значение которых нужно знать, чтобы точно понимать принципы расчета.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.
Диаметр — отрезок, соединяющий две точки на окружности и проходящий через центр окружности. Диаметр равен двум радиусам.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Число π (пи) — математическая постоянная, равная отношению длины окружности к её диаметру. Пи равняется примерно 3,14.
Площадь круга и размеры пицц
Люди не всегда верно сопоставляют площадь круга и диаметры. К примеру, сможете ли вы ответить:
Что больше: 2 пиццы диаметром 25 см или 1 пицца диаметром 40 см?
Интуитивно кажется, что 2 пиццы, так как в сумме их радиусы дают 50 сантиметров, что больше, чем 40. Однако это неправильный вывод, так как сравнивать нужно не сумму диаметров, а сумму квадратов диаметров. То есть:
- 252 + 252 = 625 + 625 = 1250
- 402 = 1600
Так как ¼π является константой, то можно сравнивать только квадраты диаметров. Получается, что пицца 40 см больше, чем даже 2 пиццы размером 25 см. А вот если диаметр пиццы составляет 35 см, то 352 = 1225, и в этом случае 2 пиццы по 25 см будут иметь бОльшую площадь.
Площади усеченных частей круга
А также полезно знать следующие геометрические элементы, связанные с кругами и окружностями:
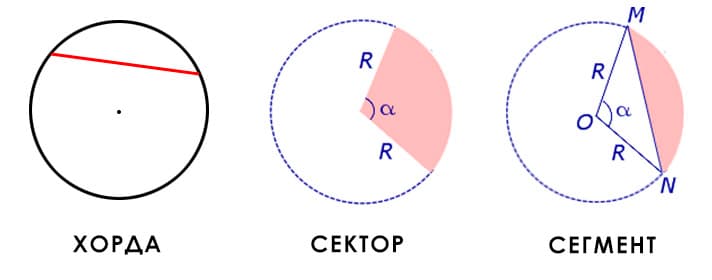
Хорда — отрезок, соединяющий любые две точки окружности.
Сектор — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Сектор является частью круга, а его площадь относится к площади круга так же, как и длина окружности сектора к длине всей окружности. Поэтому площадь сектора равна площади круга, умноженной на отношение длинны окружности сектора к длине окружности всего круга.
Но площадь сектора можно вычислить и по более простой формуле. Она равна длине дуги сектора, умноженной на половину радиуса:
S = sr/2
где S — площадь сектора, r — радиус круга.
Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой.
Площадь сегмента можно найти по формулам:
S = r2sinα/ 2
где S — площадь сегмента, sinα — синус угла двух между радиусов до концов хорды, r — радиус круга.
Часто задаваемые вопросы о площади круга?
И конечно, стоит ответить на некоторые вопросы, которые возникают во время расчетов.
Входит ли окружность (периметр) в площадь круга?
Да, входит, ведь кругом являются все точки, удаленные от центра круга на расстояние, которое не превышает радиус.
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть разнообразные калькуляторы, в частности калькуляторы: длины окружности, диаметра и площади круга. Для последней калькулятор находится на данной странице.
Хватит ли только диаметра, только радиуса или только длинны окружности для расчета площади круга?
Да, хватит чего-то одного, так как все 3 сущности можно вывести одну из другой, например, диаметр равен двум радиусам, а длина окружности – это диаметр, умноженный на число Пи.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Кто впервые научился вычислять площадь круга?
Гиппократ Хиосский (не тот, в честь которого назвали клятву) первым сформулировал, что площадь круга пропорциональна квадрату его диаметра. Евдокс Книдский в IV веке до н. э. строго доказал это утверждение. А Архимед в III веке до н. э. нашёл число Пи и продемонстрировал, что оно чуть меньше, чем 3 и 1/7.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор объема пирамиды. Рассчитайте объем пирамиды по высоте, площади основания или стороне основания. Основание может быть любой формы.
- Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии