Как найти площадь круга с помощью линейки

Как найти площадь круга с помощью линейки

Как измерить площадь круга с помощью линейки?



Ученик

(74),
закрыт



11 лет назад

Андванс Чесс

Просветленный

(31696)


11 лет назад

Как здесь некоторые товарищи сказали – нужно найти диаметр, но не указали как это сделать с помощью линейки (не на глазок, а точно)
Рассказываю.
Проводите произвольно две хорды, с помощью линейки находите середину хорды. Так как линейка по умолчанию прямоугольная, мы можем к середине хорды провести перпендикулятор.
Точка пересечения перпендикуляторов к серединам хорд – центр круга.
Остаётся только замерить расстояние от найденной середины круга до любой его точки, возвести в квадрат и умножить на пи.
Удачи!

Источник


Загрузить PDF


Загрузить PDF

Некоторые учащиеся не понимают, как найти площадь круга по исходным данным. Для начала нужно запомнить формулу, по которой вычисляется площадь круга: S=pi r^{2}. Формула проста: чтобы найти площадь круга, нужно знать только его радиус. Но нужно уметь преобразовывать другие исходные величины, чтобы воспользоваться этой формулой.

  1. Изображение с названием Calculate the Area of a Circle Step 1

    1

    Найдите радиус круга. Радиус – это отрезок, соединяющий центр круга с любой точкой внешней окружности круга. Радиус можно измерить в любом направлении: он будет одним и тем же. Радиус также равен половине диаметра круга. Диаметр – это отрезок, который проходит через центр круга и соединяет две точки внешней окружности круга.[1]

    • Как правило, значение радиуса дано в условиях задачи. Довольно трудно найти точный центр круга, если только он не обозначен на круге, который нарисован на бумаге.
    • Например, радиус круга равен 6 см.

  2. Изображение с названием Calculate the Area of a Circle Step 2

    2

    Возведите радиус в квадрат. Формула для вычисления площади круга: S=pi r^{2}, где r – радиус, который возведен во вторую степень (в квадрат).[2]

  3. Изображение с названием Calculate the Area of a Circle Step 3

    3

    Полученный результат умножьте на число Пи. Это число обозначается греческой буквой pi и представляет собой математическую константу, которая характеризует взаимосвязь радиуса и площади круга. Число Пи приблизительно равно 3,14. Точное значение числа Пи включает бесконечное количество цифр. Иногда ответ (площадь круга) записывается с постоянной pi .[3]

    • В нашем примере (r = 6 см) площадь вычисляется так:

  4. Изображение с названием Calculate the Area of a Circle Step 4

    4

    Запишите ответ. Помните, что площадь измеряется в квадратных единицах. Если радиус дан в сантиметрах, площадь измеряется в квадратных сантиметрах. Если радиус дан в миллиметрах, площадь измеряется в квадратных миллиметрах. Уточните у преподавателя, нужно ли представить ответ с постоянной pi или в числовой форме, используя приблизительное значение числа Пи. Если требование не ясно, запишите оба варианта ответа.[4]

    • В нашем примере (r = 6 см) S = 36pi см2 или S = 113,04 см2.

    Реклама

  1. Изображение с названием Calculate the Area of a Circle Step 5

    1

    Измерьте или запишите диаметр. В некоторых задачах радиус не дан. Вместо радиуса указывается диаметр. Если диаметр нарисован на бумаге, измерьте его с помощью линейки. Скорее всего, числовое значение диаметра будет задано.

    • Например, диаметр круга равен 20 мм.

  2. Изображение с названием Calculate the Area of a Circle Step 6

    2

    Разделите диаметр пополам. Помните, что диаметр равен удвоенному радиусу. Поэтому разделите любое значение диаметра на 2, чтобы найти радиус.

    • Таким образом, если диаметр круга равен 20 мм, то радиус круга равен 20/2 = 10 мм.

  3. Изображение с названием Calculate the Area of a Circle Step 7

    3

  4. Изображение с названием Calculate the Area of a Circle Step 8

    4

    Запишите ответ. Помните, что площадь измеряется в квадратных единицах. В нашем примере диаметр дан в миллиметрах, поэтому радиус тоже измеряется в миллиметрах, а площадь в квадратных миллиметрах. В нашем примере S = 100pi мм2.

    • Также ответ можно представить в численной форме, используя вместо pi приблизительное значение 3,14. В этом случае S = (100)(3,14) = 314 мм2.

    Реклама

  1. Изображение с названием Calculate the Area of a Circle Step 9

    1

    Запишите преобразованную формулу. Если известна длина окружности круга, можно воспользоваться преобразованной формулой для вычисления его площади. Такая формула включает длину окружности, а не радиус, и записывается так:

    • S={frac {C^{2}}{4pi }}

  2. Изображение с названием Calculate the Area of a Circle Step 10

    2

    Измерьте или запишите длину окружности. В некоторых ситуациях нельзя точно измерить диаметр или радиус. Если диаметр не нарисован или центр не отмечен, очень сложно найти точный центр круга. Длину окружности некоторых предметов (например, сковороды) довольно легко измерить с помощью рулетки, то есть можно найти более точное значение длины окружности, чем диаметра.[5]

    • Например, длина окружности круга (или круглого предмета) равна 42 см.

  3. Изображение с названием Calculate the Area of a Circle Step 11

    3

  4. Изображение с названием Calculate the Area of a Circle Step 12

    4

    Запишите формулу для вычисления площади круга. Запишите преобразованную формулу на основе соотношения между длиной окружности и радиусом. Подставьте последнее равенство в стандартную формулу для вычисления площади круга:[7]

  5. Изображение с названием Calculate the Area of a Circle Step 13

    5

    Воспользуйтесь преобразованной формулой, чтобы решить задачу. Теперь в формуле вместо радиуса присутствует длина окружности, поэтому можно вычислить площадь круга по известной длине окружности. Подставьте значение длины окружности и выполните вычисления следующим образом:[8]

  6. Изображение с названием Calculate the Area of a Circle Step 14

    6

    Запишите ответ. Если длина окружности дана в виде числа, а не произведения числа и pi , ответ можно записать с pi в знаменателе. Или вместо числа Пи подставьте его приблизительное значение (3,14).[9]

    Реклама

  1. Изображение с названием Calculate the Area of a Circle Step 15

    1

    Запишите известные величины. В некоторых задачах дана площадь сектора круга, по которой нужно найти площадь всего круга. Внимательно прочитайте такую задачу; ее условие может выглядеть так: «Площадь сектора круга равна 15pi см2. Найдите площадь всего круга».[10]

  2. Изображение с названием Calculate the Area of a Circle Step 16

    2

    Запомните определение сектора. Сектор круга – это часть круга, которая ограничена дугой и двумя радиусами. Пространство между такими радиусами и дугой называется сектором.[11]

  3. Изображение с названием Calculate the Area of a Circle Step 17

    3

    Измерьте центральный угол сектора. Воспользуйтесь транспортиром, чтобы измерить угол между двумя радиусами. Линейку (прямолинейную шкалу) совместите с одним из радиусов, причем центр линейки должен совпадать с центром круга. Затем найдите величину угла; для этого посмотрите на точку пересечения второго радиуса с угломерной шкалой.[12]

    • Не перепутайте внутренний и внешний угол между двумя радиусами. В задаче должно быть указано, с каким углом работать. Помните, что сумма внутреннего и внешнего углов равна 360 градусов.
    • Во многих задачах центральный угол дан, то есть измерять его не нужно. Например, в задаче может быть сказано: «Центральный угол сектора равен 45 градусов»; если это не так, измерьте центральный угол.

  4. Изображение с названием Calculate the Area of a Circle Step 18

    4

    Используйте преобразованную формулу для вычисления площади круга. Если известны площадь сектора и его центральный угол, используйте следующую преобразованную формулу, чтобы найти площадь круга: [13]

  5. Изображение с названием Calculate the Area of a Circle Step 19

    5

  6. Изображение с названием Calculate the Area of a Circle Step 20

    6

    Запишите ответ. В нашем примере сектор составлял одну восьмую полного круга. Поэтому площадь полного круга равна 120pi см2. Так как площадь сектора дана с постоянной pi , скорее всего, ответ тоже можно представить с этой постоянной.[15]

    • Чтобы записать ответ в численной форме, умножьте 120 x 3,14 = 376,8 см2.

    Реклама

Об этой статье

Эту страницу просматривали 264 354 раза.

Была ли эта статья полезной?

Источник

Как посчитать длину окружности

Онлайн калькулятор

Как посчитать длину окружности зная диаметр

Какая длина у окружности если

Какова длина окружности (С) если её диаметр d?

Формула

С = π⋅d , где π ≈ 3.14

Пример

Если диаметр круга равен 1 см, то его длина примерно равна 3.14 см.

Как посчитать длину окружности зная радиус

Какая длина у окружности если

Какова длина окружности (С) если её радиус r?

Формула

С = 2⋅π⋅r , где π ≈ 3.14

Пример

Если радиус круга равен 0.5 см, то его длина примерно равна 3.14 см.

Как посчитать длину окружности зная её площадь

Какая длина у окружности если

Какова длина окружности (С) если её площадь S?

Формула

С = 2π⋅ √ S /π , где π ≈ 3.14

Пример

Если площадь круга равна 6 см 2 , то его длина примерно равна 8.68 см.

Как измерить диаметр круга с помощью линейки

Как замерить посредством линейки или рулетки

Перед тем, как замерить диаметр трубы рулеткой или гибкой линейкой, следует знать, что этот вариант отличается простотою действий, и эта задача будет посильной даже малоопытным мастерам. Тут необходимо выполнить всего один замер.

Необходимо измерить окружность трубопровода. Значение, которое получится, делят на величину Пи. Чтобы замерить и получить более точные цифры, следует использовать в работе не 3,14, а 3,1416. Но, для задачи как найти наружный диаметр трубы с большим объемом, линейки будет не достаточно. В работу нужно будет взять рулетку.

Чтобы определить объем трубы так же используют способ измерения габарита стенки на срезе. Это можно измерить все теми же инструментами. Есть возможность также применить штангенциркуль. От размерного показателя объема снаружи отнимается показатель толщины стенок.

Выполняя монтаж магистралей, важно знать, что определить внутренний объем сортамента, импортируемого к нам, нужно определяясь на то, что его поставляют с сопроводительной документацией.

Как измерить диаметр трубы?

В ней указываются значения внутреннего объема в дюймах. Чтобы перевести показатели внутреннего или внешнего размера в сантиметры, их нужно умножить на 2,54. Для аналогичного перевода внутреннего и внешнего диам-ра обратно, следует умножить показатель на 0,398.

Ниже представлен еще интересный способ.

Как замерить с помощью штангенциркуля

Если спросить у профессионального сантехника, как замерить штангенциркулем, то ответ на этот вопрос будет следующим – «штангенциркуль для таких действий является наиболее удобным приспособлением, и замерить им нужный габарит можно очень легко не проводя дополнительных вычислений. Но, измерять таким путем только можно трубный прокат с габаритами до пятнадцати сантиметров».

Губками приспособления нужно основательно прижиматься к стенке сортамента, но прикладывать при этом большие усилия не рекомендуют. Дальше можно замерить и определить размеры в сантиметрах, и при наличии необходимости – в миллиметрах.

Так же, используя штангенциркуль, можно мерить и определить размер торцевой части. Если эта часть магистрали находится в труднодоступном месте, и соединение здесь неразъемное, то это приспособление окажется даже очень кстати.

Но, длина его ножек не должна быть больше, чем половина объема трубопровода. Для определения замера измерительное приспособление прикладывается к трубе в самом широком месте.

Измерение штангенциркулем ШЦ-1

Перед тем, как определить диаметр стальной трубы этим способом, следует запомнить, что мастера со стажем рекомендуют брать для работы только прибор высокого качества. Только он может гарантировать точное определение размеров.

Как замерить микрометром

Если определяется диаметр металлической или любой другой трубы, то каждый замер можно проделать с высокой точностью (до 0,01мм) с помощью микрометра. По своему виду, устройство напоминает скобу. На одной ее стороне находится пятка – опора, а на другой стебель и резьба высокой точности, оснащенная микровинтом. Микровинт содержит метрическую шкалу.
Чтобы узнать, как найти показатель объема сортамента посредством микрометра на металлическом или другом трубопрокате, необходимо расположить деталь между пяткой и торцом, затем начать вращение винта.

Продолжать следует до тех пор, пока не прозвучат 3 щелчка. Далее нужно найти показания на стебле, где есть шкала в миллиметрах, и к полученным цифрам добавляются данные со второй шкалы прибора (это сотые доли миллиметра). В сумме этих двоих показателей определяется нужная величина. И, как видно, найти ее совсем не сложно.

Наиболее правильно замерить диаметр трубы позволяют микрометры, оснащенные электронной функцией цифрового отсчета. Они самые удобные для работы, и позволяют определить результат с точностью до 0, 001мм. Если в таком приборе садится батарейка, то замерить им можно, как обычным микрометром.

Единственным минусом в данном случае называют высокую стоимость приборов, что не всегда приемлемо для домашнего мастера. Поэтому, чтобы правильно произвести замер в домашних условиях, такие приборы применяют крайне редко.

Лазерные датчики

Измеряться диаметр металлической или любой другой трубы круглого сечения может сканирующими лазерными датчиками. Как определяется диаметр трубы этими приборами? Здесь все просто.

Такие устройства состоят из получателя и приемника. Эти приборы используют плоскость света, образовавшуюся от лазера, который отклоняется крутящейся призмой и направляется посредством линзы.

В приемнике лазер фокусируют на диоде. Для того чтобы выполнить последующий проход лазеру по металлической или другой системе, необходимо время.

Формула окружности через диаметр

Поскольку длина очертания пропорциональна к радиусу, то и соответственно пропорциональна диаметру. Поэтому ее длину мы условно означим буквой C, диаметр — d. Поскольку соотношение длины очертания и диаметра — постоянное число, то его можно определить.

Проделав все подсчеты, мы определим число, которое приблизительно равно 3,1415… По той причине, что при подсчетах конкретное число не получилось, то обозначим его буквой π. Этот значок нам пригодится для того, чтобы была выведена формула длины окружности через диаметр.

Проведем воображаемую линию через центральную точку и измерим расстояние между двумя крайними. Это и будет диаметр. Если будем знать диаметр окружности, формула для определения длины ее самой будет выглядеть так: C = d * π.

Если мы будем определять длину разных очертаний, то если известен их диаметр, формула будет применена одна и та же. Поскольку знак π — это приблизительное исчисление, то и было решено умножать диаметр на 3,14 (число, округленное до сотых).

Замеряем штангенциркулем

С помощью этого высокоточного инструмента измеряют параметры различных конструкций. Как измерить диаметр трубы штангенциркулем? Для этого нужно развести его губки, вставить в них изделие и свести так, чтобы они прижимались к поверхности. Губки при смыкании должны быть параллельны плоскости сечения трубы, иначе измерение будет неправильным. Штангенциркулем измеряют и внутренний диаметр. С его обратной стороны есть губки, которые помещаются внутрь конструкции и разводятся до примыкания к стенкам.

Иногда требуется измерить диаметр смонтированной трубы, которая имеет слишком большие размеры. В этом случае можно измерить инструментом хорду и вычислить диаметр математическим путем. Разводим его губки на максимальное расстояние и прикладываем к трубе. Получившийся показатель – длина хорды. Для расчета понадобится также измерить высоту губок прибора. Диаметр вычисляется по формуле:

Если губки имеют слишком большую длину, то можно подложить какую-нибудь деталь (брусок и т.д.). Тогда высота будет рассчитываться по формуле:

Наружный и внутренний диаметр

Чаще всего этот параметр конструкции измеряется в дюймах, которые легко переводятся в сантиметры (значение умножается на 2,54). Прежде всего, следует определиться, что нужно измерить: внутренний диаметр трубы или наружный. Изделия, используемые для водо- и газоснабжения, обычно замеряются по внутреннему диаметру. Это связано с тем, что данный показатель определяет пропускную способность конструкции.

Наружный диаметр может иметь разные значения в зависимости от толщины стенки (от нее зависит механическая прочность всего изделия). Согласно ГОСТ 355–52, каждый следующий диаметр трубы отличается от предыдущего лучшей пропускной способностью (на 50%). Проходимость конструкции часто называют условным (номинальным) диаметром. При этом показатель обычно отличается от внутреннего диаметра (на 1-10 мм). Этот важный параметр считается основной характеристикой изделия, от которой отталкиваются в процессе проектирования и монтажа.

Как найти диаметр окружности

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости.

Круг — часть плоскости, лежащая внутри окружности, а также сама окружность.

Если говорить проще, окружность — это замкнутая линия, как, например, обруч и велосипедное колесо. Круг — часть плоскости, ограниченная окружностью, как блинчик или вырезанный из картона кружок.

Диаметр — отрезок, который соединяет две точки окружности и проходит через ее центр.

Радиус — отрезок, который соединяет центр окружности и любую точку на ней.

Как узнать диаметр. Формулы

В данной теме нам предстоит узнать три формулы:

1. Общая формула.

Исходя из основных определений нам известно, что значение диаметра равно двум радиусам: D = 2 × R, где D — диаметр, R — радиус.

2. Если перед нами стоит задача найти диаметр по длине окружности

D = C : π, где C — длина окружности, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14.

Чтобы получить правильный ответ, можно поделить столбиком или использовать онлайн-калькулятор.

3. Если есть чертеж окружности

  • Начертить внутри круга прямую горизонтальную линию. Ее месторасположение не играет значительной роли.
  • Отметить точки пересечения прямой и окружности.
  • Начертить при помощи циркуля две окружности одного радиуса (больше, чем радиус первоначальной окружности), первую — с центром в точке A, вторую — с центром в точке B.
  • Провести прямую через две точки, в которых произошло пересечение. Отметить точки пересечения полученной прямой с окружностью. Диаметр равен этому отрезку.
  • Теперь осталось измерить диаметр круга при помощи линейки. Получилось!

Эти простые формулы могут пригодиться не только на школьных уроках, но и если вы решите освоить профессию дизайнера интерьера, архитектора или модельера одежды.

[spoiler title=”источники:”]

http://nordtool.ru/novosti/kak-uznat-diametr.html

http://skysmart.ru/articles/mathematic/diametr-okruzhnosti

[/spoiler]

Источник
  1. Главная
  2. Справочники
  3. Справочник по математике 5-9 класс
  4. Отношения и пропорции
  5. Длина окружности и площадь круга

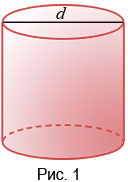
Возьмем цилиндр, диаметр основания которого равен 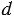(рис.1).

Мы можем измерить его диаметр, высоту с помощью линейки, при этом мы не можем измерить с ее помощью длину окружности его основания. Чтобы ее измерить воспользуемся нитью, обернем ее вокруг цилиндра и отрежем так, чтобы оно образовала замкнутую окружность (рис. 2).

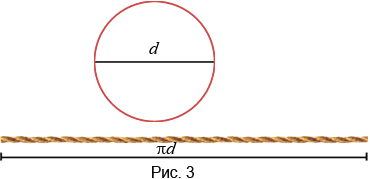
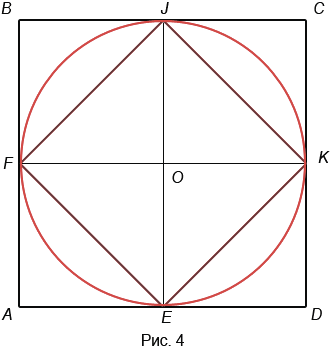
Тогда если мы ее развернем, то она будет приближенно равна длине окружности основания цилиндра (рис. 3).

Заметим, что если диаметр основания увеличить, то длина веревки, которая понадобиться, чтобы “опоясать” цилиндр, также увеличится.

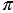
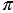
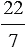
Из этого следует, что отношение длины окружности к длине её диаметра является одним и тем же числом для всех окружностей. Данное число обозначают буквой (“пи”). При этом на практике найдено, что с точностью до десятитысячных равно 3,1416 (примерно такую же точность дает значение ).

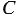
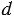
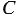
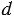
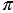
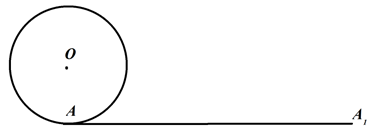
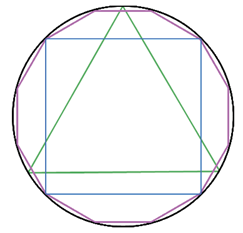
Пусть – длина окружности, – длина диаметра, тогда : = , откуда 

Изобразим  круг с центром в точке О, радиус которого равен 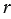, и два квадрата ABCD и ЕFJK (см. рисунок 4):

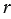
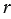
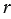
Так как по построению радиус окружности равен , то длина стороны квадрата ABCD, равная диаметру окружности, будет равна 2, тогда его площадь будет равна 42.

Диагональ FE делит квадрат AEOF на два равных треугольника, значит, площадь треугольника EOF в два раза меньше площади квадрата AEOF, поэтому площадь квадрата ЕFJK  в два раза меньше площади квадрата ABCD, значит, площадь квадрата ЕFJK  равна 2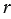2.

Если мы посмотрим на рисунок 4, то заметим, что площадь круга S, меньше площади квадрата ABCD, но больше площади квадрата ЕFJK, поэтому мы можем записать неравенство:

22 < S < 42.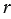

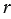
В курсе геометрии будет доказано, что S = 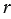2.

Советуем посмотреть:

Отношения

Пропорции

Прямая и обратная пропорциональные зависимости

Отношения и пропорции


Правило встречается в следующих упражнениях:

6 класс

Номер 747,
Мерзляк, Полонский, Якир, Учебник

Номер 750,
Мерзляк, Полонский, Якир, Учебник

Номер 756,
Мерзляк, Полонский, Якир, Учебник

Номер 759,
Мерзляк, Полонский, Якир, Учебник

Номер 775,
Мерзляк, Полонский, Якир, Учебник

Номер 776,
Мерзляк, Полонский, Якир, Учебник

Номер 3,
Мерзляк, Полонский, Якир, Учебник

Задание 850,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 853,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 886,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

7 класс

Номер 19,
Мерзляк, Полонский, Якир, Учебник

Номер 20,
Мерзляк, Полонский, Якир, Учебник

Номер 545,
Мерзляк, Полонский, Якир, Учебник

Номер 1225,
Мерзляк, Полонский, Якир, Учебник

Источник


Длина окружности и площадь круга

План урока

  • Длина окружности;
  • Число Пи;
  • Площадь круга;
  • Площадь кругового сектора.

Цели урока

  • Знать формулы длины окружности и длины дуги;
  • Уметь применять формулы длины окружности и длины дуги для решения задач;
  • Знать какое число обозначается буквой π и чему равно его приближенное значение;
  • Знать определения круга, кругового сектора и кругового сегмента;
  • Знать формулы площади круга, площади кругового сектора и кругового сегмента;
  • Уметь выводить формулы площади круга, площади кругового сектора и кругового сегмента, применять их при решении задач.

Разминка

  • Какой многоугольник называется правильным?
  • Можно ли правильные многоугольники вписать в окружность?
  • Можно ли описать окружность около правильного многоугольника?
  • Чем круг отличается от окружности?
  • Что такое дуга? Хорда?

Длина окружности

Для начала вспомним, что такое окружность.

Окружность – это геометрическое место точек, равноудаленных от данной точки. Эта точка называется центром окружности.


Рис. 1. Длина окружности

Чтобы получить наглядное представление о длине окружности, представим себе, что окружность сделана из нерастяжимой нити. Если разрезать эту нить в какой-нибудь точке и распрямить, то получится отрезок, длина которого будет равна длине окружности (рис.1).


Рис. 2. Приближенное значение длины окружности

Если около правильного многоугольника описать окружность, то периметр этого многоугольника является приближенным значением длины окружности. Это приближенное значение длины окружности при увеличении числа сторон многоугольника становится практически равным периметру многоугольника (рис.2). Такое значение длины окружности – это предел, к которому стремится периметр правильного вписанного в окружность многоугольника при неограниченном увеличении числа его сторон.

Выведем формулу, выражающую длину окружности через её радиус.

Пусть C и C1 – длины окружностей радиусов R и R1. В каждую из этих окружностей впишем правильный n-угольник. Пусть P и P1 – периметры этих 
n-угольников, а anи a’n – их стороны. По формуле стороны правильного многоугольника an=2R sin180°n, можно выразить периметр:

P=n·an=n·2R sin180°n

P1=n·a’n=n·2R1 sin180°n

Тогда можно составить отношение
 

PP1=2R2R1.

При любых значениях n это равенство имеет место. Теперь будем неограниченно увеличивать значение n. При n→∞ P→C, P1→C1, тогда предел отношения  PP1равен CC1. Но, с другой стороны, этот предел равен отношению 2R2R1. Таким образом, получаем:

CC1=2R2R1.

Из этого равенства несложно получить:

C2R=C12R1.

В итоге мы показали, что отношение длины окружности к ее диаметру есть одно и то же число для всех окружностей. Это число принято обозначать как π (читается «пи»).

Тогда из равенства C2R=π получим формулу для вычисления длины окружности:

C=2πR

Длина C окружности находится по формуле:

C=2πR,

где R – радиус окружности, π – число, приближенно равное 3,14.

Длина l дуги окружности находится по формуле:

l=πR180·α,

где R – радиус окружности, π – число, приближенно равное 3,14, α – градусная мера дуги окружности.

Докажем вторую формулу. Длина всей окружности равна 2πR, тогда длина дуги окружности, равной 1°, будет равна 2πR360=πR180, Получили, что длина дуги с градусной мерой α будет равна πR180·α.

Пример 1

Найдите длину окружности, если её диаметр равен 10.

Решение

Сначала найдем радиус окружности R как половину диаметра: 

R=10:2=5.

Вычислим длину окружности по формуле C=2πR, приняв число π=3,14:

C=2·3,14·5=31,4

Ответ: 31,4.

Упражнение 1

1. Найдите длину окружности, если её диаметр равен 18 (π=3,14).

2. Найдите длину l дуги окружности, если R=54, градусная мера дуги α=30° (π=3,14).

Число пи

Для всех окружностей отношение длины окружности к ее диаметру – это одно и то же число. Его принято обозначать греч. буквой π (читается «пи»).

π=3,14159265…

Это бесконечная непериодическая десятичная дробь.

Обозначение числа π происходит от первой буквы греческих слов периферия, что означает «окружность» и периметр. 

Рациональное число 227 является приближенным значением числа π с точностью до 0,002. Это приближенное значение было найдено ещё в III в. до н. э. великим греческим ученым Архимедом. 

В XX в. с приходом компьютерных систем и вычислительной техники дело пошло быстрее: теперь уже точные десятичные значения высчитывали машины. С помощью специальных алгоритмов математики во всем мире продолжают определять новые, более точные значения числа пи, устанавливая рекорды по количеству цифр десятичного разложения (после запятой в десятичной дроби).

При решении задач обычно используют приближенное значение числа π, равное 3,14.

Площадь круга


Круг
 – это часть плоскости, ограниченная окружностью.

Площадь круга равна квадрату радиуса, умноженному на отношение длины окружности к ее диаметру, т.е.

S=πR2.


Рис. 3. Площадь круга

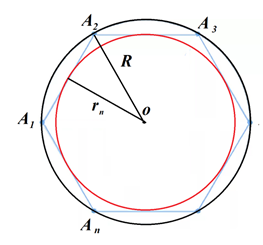
Докажем эту формулу. Пусть дан круг радиуса R и с центром в точке O(рис. 3). 

Впишем в круг какой-нибудь правильный многоугольник A1A2A3…An. Легко заметить, что площадь круга  S будет больше площади правильного многоугольника Sn, ведь многоугольник целиком лежит в круге. В многоугольник A1A2A3…An впишем круг радиуса rn с центром в точке O. Его площадь S’ будет меньше площади Sn многоугольника A1A2A3…An, так как круг целиком лежит в многоугольнике. Таким образом, можно записать неравенство:

S'<Sn<S

Представим себе, что число сторон правильного многоугольника неограниченно увеличивается, т.е. n→∞. По изученной ранее формуле: rn=Rcos180°n, где rn – радиус вписанной окружности, а R – радиус описанной окружности. При  n→∞ значение cos180°n→1, значит  rn→R. 

Мы получили, что при неограниченном увеличении сторон правильного многоугольника вписанная в него окружность «стремится» к описанной окружности, и тогда Sn→S при n→∞. 

Из формулыSn=12Pnrn, где Pn – периметр многоугольника A1A2A3…An, учитывая, что rn→R, Pn→2πR, Sn→S при  n→∞, получим:

S=122πR·R=πR2.

Задача

Построить с помощью циркуля и линейки квадрат, равновеликий данному кругу (равновеликие – имеющие одинаковую площадь).

Эта задача, известная под названием 
квадратуры круга
, не может быть решена. Действительно, если обозначить буквой x сторону искомого квадрата, а буквой R радиус круга, то получим уравнение:

x2=πR2,     πR:x=x:R

т.е. x есть среднее пропорциональное между полуокружностью и радиусом. Значит, если известен отрезок, длина которого равна длине полуокружности, то легко построить квадрат, равновеликий данному кругу, и обратно: если известна сторона квадрата, равновеликого кругу, то можно построить отрезок, равный по длине полуокружности. Но с помощью циркуля и линейки нельзя построить отрезок, длина которого равнялась бы длине полуокружности; следовательно, нельзя в точности решить задачу о построении квадрата, равновеликого кругу. Приближенное решение можно выполнить, если предварительно найти приближенную длину полуокружности и затем построить среднее пропорциональное между отрезком этой длины и радиусом.

Пример 2

Найдите площадь круга, если его диаметр равен 12 π≈3,14.

Решение

Найдем радиус круга, как половину диаметра:

R=12:2=6

Вычислим площадь круга по формуле S=πR2:

S=3,14·62=113,04

Ответ: 113,04.

Площадь кругового сектора


Круговым сектором
 (или просто
сектором
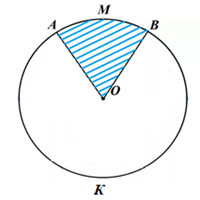
) называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга (рис. 4).


Рис. 4. Круговой сектор

На рисунке 4 изображено два круговых сектора. Первый закрашенный сектор с дугой АМВ и второй сектор с дугой АКВ.

Площадь кругового сектора находится по формуле: 

S=πR2360·α, где R – радиус кругового сектора, α – градусная мера дуги, ограничивающей сектор.

Действительно, так как площадь всего круга равна πR2, то площадь сектора, ограниченного дугой в 1°, будет составлять πR2360. Поэтому площадь сектора, ограниченного дугой с градусной мерой α будет составлять πR2360·α.


Круговым сегментом
 или просто
сегментом
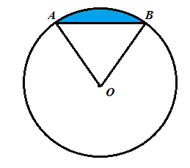
 называется часть круга, ограниченная дугой окружности и хордой, соединяющей концы этой дуги (рис. 5).


Рис. 5. Круговой сегмент

Очевидно, что если градусная мера дуги меньше 180°, то площадь сегмента легко найти, вычитая из площади сектора площадь равнобедренного треугольника, сторонами которого являются два радиуса и хорда сегмента.

Пример 3

Из круга, радиус которого равен 20 см, вырезан сектор с дугой в 90°. Чему равна площадь оставшейся части круга? π≈3,14.

Решение

Найдем площадь всего круга:

S=πR2=3,14·202=1256 (см2).

Найдем площадь сектора

S=πR2360·α=3,14·202360·90=314 (см2).

Найдем площадь оставшейся части круга. Для этого из площади круга вычтем площадь сектора:

S=1256-314=942 (см2).

Ответ: 942 см2.

Упражнение 2

1. Найдите площадь круга, если его диаметр равен 24 (π=3,14).

2. Из круга, радиус которого равен 30 см, вырезан сектор с дугой в 60°. Чему равна площадь оставшейся части круга (π=3,14)?

Контрольные вопросы

1. Выведите формулу для вычисления длины окружности

2. Чему равно число π? Что оно означает?

3. Что такое круг?

4. Выведите формулу для вычисления площади круга

5. Что называется круговым сектором? Чему равна его площадь?

6. Что называется круговым сегментом? Чему равна его площадь?

Ответы

Упражнение 1

1. 56,52.  

2. 28,26

Упражнение 2

1. 452,16. 

2. 2355 см2.

Источник

Добавить комментарий