Как найти площадь круга вписанного в четырехугольник

Окружность, вписанная в четырехугольник

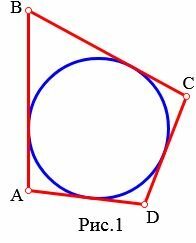
Определение 1. Окружность называют вписанным в четырехугольник, если окружность касается всех сторон четырехугольника.

На рисунке 1 окружность вписан в четырехугольник ABCD. В этом случае говорят также, что четырехугольник описан около окружности.

Теорема 1. Если окружность вписан в четырехугольник, то сумма противолежащих сторон четырехугольника равны.

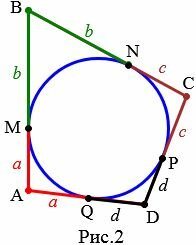
Доказательство. Пусть окружность ABCD вписан в четырехугольник (Рис.2). Докажем, что ( small AB+CD=AD+BC ).

Точки M, N, Q, P − точки касания окружности со сторонами четырехугольника. Так как отрезки касательных, проведенных к окружности через одну точку, равны (статья Касательная к окружности теорема 2), то

( small AM=AQ=a, ) ( small BM=BN=b, ) ( small CN=CP=c, ) ( small DQ=DP=d )

( small AB+CD ) ( small=AM+BM+CP+DP ) ( small =a+b+c+d, )

(1)

( small AD+BC) ( small=AQ+DQ+BN+CN) ( small=a+d+b+c. )

(2)

Из равенств (1) и (2), следует:

( small AB+CD=AD+BC. )

Теорема 2. Если в выпуклом четырехугольнике сумма противолежащих сторон равны, то в него можно вписать окружность.

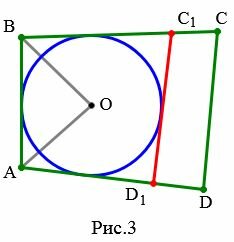
Доказательство. Пусть задан выпуклый четырехугольник ABCD и пусть ( small AB+CD=AD+BC. ) (Рис.3). Докажем, что в него можно вписать окружность.

Проведем биссектрисы углов A и B четырехугольника ABCD. Точку их пересечения обозначим буквой O. Тогда точка O равноудалена от сторон AB, BC, AD. Следовательно существует окружность с центром в точке O, которая касается этих трех сторон.

Пусть эта окружность не касается стороны CD. Тогда возможны два случая.

Случай 1. Сторона CD не имеет общих точек с построенной окружностью.

Проведем касательную C₁D₁ к окружности, параллельно стороне CD четырехугольника.

Тогда окружность с центром O вписан в четырехугольник ABC₁D₁. Следовательно, по теореме 1, имеем:

( small AB+C_1D_1=AD_1+BC_1. )

(3)

Но по условию данной теоремы:

( small AB+CD=AD+BC. )

(4)

Вычтем из равенства (4) равенство (3):

( small CD-C_1D_1) (small=AD-AD_1+BC-BC_1 )

( small CD-C_1D_1=DD_1+CC_1 )

( small CD=DD_1+CC_1+C_1D_1)

Получили, что в четырехугольнике CC₁D₁D длина одной стороны равна сумме длин трех остальных сторон, что невозможно (см. задачу 1 статьи Четырехугольник).

Таким образом сторона CD должна иметь общие точки с рассматриваемой окружностью.

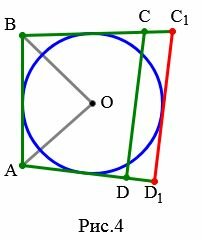
Случай 2. Сторона CD имеет две общие точки с построенной окружностью (Рис.4).

Аналогичными рассуждениями можно показать, что сторона CD не может иметь две общие точки с построенной окружностью.

Следовательно, предполагая, что построенная окружность не касается стороны CD, мы пришли к противоречию. Таким образом, если в выпуклом четырехугольнике сумма противолежащих сторон равны, то в него можно вписать окружность.

Если в четырехугольник вписан окружность, то существует точка, равноудаленная от всех сторон четырехугольника. Эта точка является центром вписанной в четырехугольник окружности. Для нахождения этой точки достаточно найти точку пересечениия биссектрис двух соседних углов данного четырехугольника.

Вписанная в четырехугольник окружность

Описанный четырехугольник — это четырехугольник, все стороны которого касаются окружности. При этом окружность называется вписанной в четырехугольник.

Какими свойствами обладает вписанная в четырехугольник окружность? Когда в четырехугольник можно вписать окружность? Где находится центр вписанной окружности?

В четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противолежащих сторон равны.

В четырехугольник ABCD можно вписать окружность, если

И обратно, если суммы противоположных сторон четырехугольника равны:

то в четырехугольник ABCD можно вписать окружность.

Центр вписанной в четырехугольник окружности — точка пересечения его биссектрис.

O — точка пересечения биссектрис четырехугольника ABCD.

AO, BO, CO, DO — биссектрисы углов четырехугольника ABCD,

то есть ∠BAO=∠DAO, ∠ABO=∠CBO и т.д.

3. Точки касания вписанной окружности, лежащие на сторонах, выходящих из одной вершины, равноудалены от этой вершины.

AM=AN,

5. Площадь четырехугольника связана с радиусом вписанной в него окружности формулой

где p — полупериметр четырехугольника.

Так как суммы противолежащих сторон описанного четырехугольника равны, полупериметр равен любой из пар сумм противолежащих сторон.

Например, для четырехугольника ABCD p=AD+BC или p=AB+CD и

Соответственно, радиус вписанной в четырехугольник окружности равен

В четырехугольник вписана окружность как найти площадь

Площади четырехугольников

В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:

которая позволяет найти площадь прямоугольника прямоугольника с основанием a и высотой b.

Формулы для площадей четырехугольников

Четырехугольник	Рисунок	Формула площади	Обозначения
Прямоугольник		S = ab

a и b – смежные стороны

d – диагональ,
φ – любой из четырёх углов между диагоналями

Получается из верхней формулы подстановкой d=2R

R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями

Параллелограмм

a – сторона,
h_a – высота, опущенная на эту сторону

a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

Квадрат

S = a 2

a – сторона квадрата

S = 4r 2

Получается из верхней формулы подстановкой d = 2R

Ромб

a – сторона,
h_a – высота, опущенная на эту сторону

a – сторона,
φ – любой из четырёх углов ромба

r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

Трапеция

a и b – основания,
h – высота

S = m h

φ – любой из четырёх углов между ними

a и b – основания,
c и d – боковые стороны

Дельтоид

S = ab sin φ

a и b – неравные стороны,
φ – угол между ними

a и b – неравные стороны,
φ₁ – угол между сторонами, равными a ,
φ₂ – угол между сторонами, равными b .

a и b – неравные стороны,
r – радиус вписанной окружности

Произвольный выпуклый четырёхугольник

φ – любой из четырёх углов между ними

Вписанный четырёхугольник

,

a, b, c, d – длины сторон четырёхугольника,
p – полупериметр,

Формулу называют «Формула Брахмагупты»

где
a и b – смежные стороны

где
d – диагональ,
φ – любой из четырёх углов между диагоналями

где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями

Формула получается из верхней формулы подстановкой d = 2R

где
a – сторона,
h_a – высота, опущенная на эту сторону

где
a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

Получается из верхней формулы подстановкой d = 2R

где
a – сторона,
h_a – высота, опущенная на эту сторону

где
a – сторона,
φ – любой из четырёх углов ромба

где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

где
a и b – основания,
h – высота

φ – любой из четырёх углов между ними

где
a и b – основания,
c и d – боковые стороны

где
a и b – неравные стороны,
φ – угол между ними

где
a и b – неравные стороны,
r – радиус вписанной окружности

φ – любой из четырёх углов между ними

,

где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр

Формулу называют «Формула Брахмагупты»

Прямоугольник
Параллелограмм
Квадрат
	S = a 2 где a – сторона квадрата
	S = 4r 2
Ромб
Трапеция
Дельтоид
	где a и b – неравные стороны, φ1 – угол между сторонами, равными a , φ2 – угол между сторонами, равными b .
Произвольный выпуклый четырёхугольник
Вписанный четырёхугольник

Прямоугольник

где
a и b – смежные стороны

где
d – диагональ,
φ – любой из четырёх углов между диагоналями

где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями

Формула получается из верхней формулы подстановкой d = 2R

Параллелограмм

где
a – сторона,
h_a – высота, опущенная на эту сторону

где
a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

Квадрат

где
a – сторона квадрата

Получается из верхней формулы подстановкой d = 2R

Ромб

где
a – сторона,
h_a – высота, опущенная на эту сторону

где
a – сторона,
φ – любой из четырёх углов ромба

где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

Трапеция

где
a и b – основания,
h – высота

φ – любой из четырёх углов между ними

где
a и b – основания,
c и d – боковые стороны ,

Дельтоид

где
a и b – неравные стороны,
φ – угол между ними

где
a и b – неравные стороны,
φ₁ – угол между сторонами, равными a ,
φ₂ – угол между сторонами, равными b .

где
a и b – неравные стороны,
r – радиус вписанной окружности

Произвольный выпуклый четырёхугольник

φ – любой из четырёх углов между ними

Вписанный четырёхугольник

где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр

Формулу называют «Формула Брахмагупты»

Вывод формул для площадей четырехугольников

Утверждение 1 . Площадь выпуклого четырёхугольника можно найти по формуле

Доказательство . В соответствии с рисунком 1 справедливо равенство:

что и требовалось доказать.

Утверждение 2 . Площадь параллелограмма параллелограмма можно найти по формуле

где a – сторона параллелограмма, а h_a – высота высота высота , опущенная на эту сторону (рис. 2).

Доказательство . Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому

что и требовалось доказать.

Утверждение 3 .Площадь параллелограмма параллелограмма можно найти по формуле

где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).

то, в силу утверждения 2, справедлива формула

что и требовалось доказать.

Утверждение 4 . Площадь ромба ромба можно найти по формуле

,

где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).

что и требовалось доказать.

Утверждение 5 . Площадь трапеции можно найти по формуле

,

где a и b – основания трапеции, а h – высота высота высота (рис.5).

Доказательство . Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD . Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF . Поэтому

что и требовалось доказать.

Утверждение 6 . Площадь трапеции трапеции можно найти по формуле

где a и b – основания, а c и d – боковые стороны трапеции ,

(рис.6).

Доказательство . Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):

,

что и требовалось доказать.

Утверждение 7 . Площадь дельтоида, дельтоида, можно найти по формуле:

где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).

Доказательство . Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D , а биссектрисы углов A и C пересекаются в некоторой точке O , лежащей на диагонали BD . Точка O и является центром вписанной в дельтоид окружности.

Если r – радиус вписанной в дельтоид окружности, то

Окружность, вписанная в четырехугольник

Определение 1. Окружность называют вписанным в четырехугольник, если окружность касается всех сторон четырехугольника.

На рисунке 1 окружность вписан в четырехугольник ABCD. В этом случае говорят также, что четырехугольник описан около окружности.

Теорема 1. Если окружность вписан в четырехугольник, то сумма противолежащих сторон четырехугольника равны.

Доказательство. Пусть окружность ABCD вписан в четырехугольник (Рис.2). Докажем, что ( small AB+CD=AD+BC ).

Точки M, N, Q, P − точки касания окружности со сторонами четырехугольника. Так как отрезки касательных, проведенных к окружности через одну точку, равны (статья Касательная к окружности теорема 2), то

( small AM=AQ=a, ) ( small BM=BN=b, ) ( small CN=CP=c, ) ( small DQ=DP=d )

( small AB+CD ) ( small=AM+BM+CP+DP ) ( small =a+b+c+d, )

(1)

( small AD+BC) ( small=AQ+DQ+BN+CN) ( small=a+d+b+c. )

(2)

Из равенств (1) и (2), следует:

( small AB+CD=AD+BC. )

Теорема 2. Если в выпуклом четырехугольнике сумма противолежащих сторон равны, то в него можно вписать окружность.

Доказательство. Пусть задан выпуклый четырехугольник ABCD и пусть ( small AB+CD=AD+BC. ) (Рис.3). Докажем, что в него можно вписать окружность.

Проведем биссектрисы углов A и B четырехугольника ABCD. Точку их пересечения обозначим буквой O. Тогда точка O равноудалена от сторон AB, BC, AD. Следовательно существует окружность с центром в точке O, которая касается этих трех сторон.

Пусть эта окружность не касается стороны CD. Тогда возможны два случая.

Случай 1. Сторона CD не имеет общих точек с построенной окружностью.

Проведем касательную C₁D₁ к окружности, параллельно стороне CD четырехугольника.

Тогда окружность с центром O вписан в четырехугольник ABC₁D₁. Следовательно, по теореме 1, имеем:

( small AB+C_1D_1=AD_1+BC_1. )

(3)

Но по условию данной теоремы:

( small AB+CD=AD+BC. )

(4)

Вычтем из равенства (4) равенство (3):

( small CD-C_1D_1) (small=AD-AD_1+BC-BC_1 )

( small CD-C_1D_1=DD_1+CC_1 )

( small CD=DD_1+CC_1+C_1D_1)

Получили, что в четырехугольнике CC₁D₁D длина одной стороны равна сумме длин трех остальных сторон, что невозможно (см. задачу 1 статьи Четырехугольник).

Таким образом сторона CD должна иметь общие точки с рассматриваемой окружностью.

Случай 2. Сторона CD имеет две общие точки с построенной окружностью (Рис.4).

Аналогичными рассуждениями можно показать, что сторона CD не может иметь две общие точки с построенной окружностью.

Следовательно, предполагая, что построенная окружность не касается стороны CD, мы пришли к противоречию. Таким образом, если в выпуклом четырехугольнике сумма противолежащих сторон равны, то в него можно вписать окружность.

Если в четырехугольник вписан окружность, то существует точка, равноудаленная от всех сторон четырехугольника. Эта точка является центром вписанной в четырехугольник окружности. Для нахождения этой точки достаточно найти точку пересечениия биссектрис двух соседних углов данного четырехугольника.

Вписанная окружность

Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.

Окружность, точно можно вписать в такие геометрические фигуры, как:

• Треугольник
• Выпуклый, правильный многоугольник
• Квадрат
• Равнобедренная трапеция
• Ромб

В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.

Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.

Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.

Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.

Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.

Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.

Свойства вписанной окружности

В треугольник

1. В любой треугольник может быть вписана окружность, причем только один раз.
2. Центр вписанной окружности — точка пересечения биссектрис треугольника.
3. Вписанная окружность касается всех сторон треугольника.
4. Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:

[ S = frac (a+b+c) cdot r = pr ]

p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.

Центр окружности вписанной в треугольник равноудален от всех сторон.

Точка касания — это точка, в которой соприкасается
окружность и любая из сторон треугольника.

От центра вписанной окружности можно провести
перпендикуляры к любой точке касания.

Вписанная в треугольник окружность делит стороны
треугольника на 3 пары равных отрезков.

Вписанная и описанная около треугольника окружность тесно взаимосвязаны.
Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера:

с — расстояние между центрами вписанной и описанной окружностей треугольника.
R — радиус описанной около треугольника.
r — радиус вписанной окружности треугольника.

В четырехугольник

1. Не во всякий четырехугольник можно вписать окружность.
2. Если у четырехугольника суммы длин его противолежащих
   сторон равны, то окружность, может быть, вписана (Теорема Пито).
3. Центр вписанной окружности и середины двух
   диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона).
4. Точка пересечения биссектрис — это центр вписанной окружности.
5. Точка касания — это точка, в которой соприкасается
   окружность и любая из сторон четырехугольника.
6. Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:

[ S = frac (a+b+c+d)cdot r = pr ]

p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.

Точка касания вписанной окружности, которая лежит на любой из сторон,
равноудалены от этой конца и начала этой стороны, то есть от его вершин.

Примеры вписанной окружности

Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.

Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.

Верные и неверные утверждения

1. Радиус вписанной окружности в треугольник и радиус вписанной
   в четырехугольник вычисляется по одной и той же формуле. Верное утверждение.
2. Любой параллелограмм можно вписать в окружность. Неверное утверждение.
3. В любой четырехугольник можно вписать окружность. Неверное утверждение.
4. В любой ромб можно вписать окружность. Верное утверждение.
5. Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
6. Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
7. Угол вписанный в окружность равен соответствующему центральному
   углу опирающемуся на ту же дугу. Неверное утверждение.
8. Радиус вписанной окружности в прямоугольный треугольник равен
   половине разности суммы катетов и гипотенузы. Верное утверждение.
9. Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
10. Вписанная окружность в треугольник имеет в общем
    три общие точки со всеми сторонами треугольника. Верное утверждение.

Окружность вписанная в угол

Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.

Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.

К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.

Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.

[spoiler title=”источники:”]

http://b4.cooksy.ru/articles/v-chetyrehugolnik-vpisana-okruzhnost-kak-nayti-ploschad

[/spoiler]

Определение.

Описанный четырехугольник — это четырехугольник, все стороны которого касаются окружности. При этом окружность называется вписанной в четырехугольник.

Какими свойствами обладает вписанная в четырехугольник окружность? Когда в четырехугольник можно вписать окружность? Где находится центр вписанной окружности?

Теорема 1.

В четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противолежащих сторон равны.

В четырехугольник ABCD можно вписать окружность, если

AB+CD=BC+AD.

И обратно, если суммы противоположных сторон четырехугольника равны:

AB+CD=BC+AD,

то в четырехугольник ABCD можно вписать окружность.

Теорема 2.

Центр вписанной в четырехугольник окружности — точка пересечения его биссектрис.

O — точка пересечения биссектрис четырехугольника ABCD.

AO, BO, CO, DO — биссектрисы углов четырехугольника ABCD,

то есть ∠BAO=∠DAO, ∠ABO=∠CBO и т.д.

3. Точки касания вписанной окружности, лежащие на сторонах, выходящих из одной вершины, равноудалены от этой вершины.

AM=AN,

BM=BK,

CK=CF,

DF=DN

(как отрезки касательных, проведенных из одной точки).

4.

   

   

   

   

(как радиусы, проведенные в точки касания).

5. Площадь четырехугольника связана с радиусом вписанной в него  окружности формулой

   

где p — полупериметр четырехугольника.

Так как суммы противолежащих сторон описанного четырехугольника равны, полупериметр равен любой из пар сумм противолежащих сторон.

Например, для четырехугольника ABCD p=AD+BC или p=AB+CD и

   

или

   

Соответственно, радиус вписанной в четырехугольник окружности равен

   

Для описанного четырехугольника ABCD

   

или

   

Геометрия,


вопрос задал lokkee,


8 лет назад

Ответы на вопрос

Ответил Аноним

0

сторона= диаметру круга вписанного в правильный четырехугольник

S=pi*r^2=pi*5 ^2=25pi

Ответил gematogen

0

потомучто правильный четырех угольник-квадрат

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Литература,
5 лет назад

Кладовая солнца. Как связано человек и природа ?

Физика,
5 лет назад

Тело брошено вертикально вверх со скоростью 10 м/с. Чему равна кинетическая энергия на высоте 1,5 метра?

Геометрия,
8 лет назад

На стороне  AB треугольника ABC, как на диаметре, построен круг, который пересекает стороны  AC и BC в точках D и E соответственно. Найдите угол CBD,  если площади треугольников DCE и ABC относятся…

История,
8 лет назад

Какую клятву довали новгородские ратники перед боем?!

Физика,
8 лет назад

Тепловая машина за цикл, получает от нагревателя количество теплоты = 100Дж и отдает холодильнику 60Дж. Найти КПД машины.

Химия,
8 лет назад

помогите я вас умоляю!!мне очень срочно!!
найти массу 10% раствора бромной воды, необходимого для полного бромирования 2,8 литра технического ацетилена, содержащего 5% примесей…

Как найти площадь вписанной окружности

Площадь окружности, вписанной в многоугольник, можно вычислить не только через параметры самой окружности, но через различные элементы описанной фигуры – стороны, высоту, диагонали, периметр.

Инструкция

Окружность называется вписанной в многоугольник, если имеет общую точку с каждой стороной описанной фигуры. Центр вписанной в многоугольник окружности всегда лежит в точке пересечения биссектрис его внутренних углов. Площадь, ограниченная окружностью, определяется формулой S=π*r²,
где r – радиус окружности,
π – число «Пи» – математическая постоянная, равная 3,14.

Для окружности, вписанной в геометрическую фигуру, радиус равен отрезку от центра до точки касания со стороной фигуры. Следовательно, можно определить зависимость между радиусом вписанной в многоугольник окружности и элементами данной фигуры и выразить площадь окружности через параметры описанного многоугольника.

В любой треугольник возможно вписать единственную окружность с радиусом, определяемым формулой: r=s∆/p∆,
где r – радиус вписанной окружности,
s∆ – площадь треугольника,
p∆ – полупериметр треугольника.

Подставьте полученное значение радиуса, выраженное через элементы описанного около окружности треугольника, в формулу площади окружности. Тогда площадь S окружности, вписанной в треугольник с площадью s∆ и полупериметром p∆ вычисляется по формуле:
S = π*(s∆/p∆)².

Окружность можно вписать в выпуклый четырехугольник при условии, что в нем равны суммы противолежащих сторон.
Площадь S окружности, вписанной в квадрат со стороной a, равна: S= π*a²/4.

В ромбе площадь S вписанной окружности равна: S= π*(d₁d₂/4a)². В этой формуле d₁ и d₂ — диагонали ромба, а – сторона ромба.
Для трапеции площадь S вписанной в нее окружности определяется по формуле: S= π*(h/2)², где h – высота трапеции.

Сторона а правильного шестиугольника равна радиусу вписанной в него окружности, площадь S окружности вычисляется по формуле: S = π*a².

Окружность можно вписать в правильный многоугольник с любым количеством сторон. Общая формула для определения радиуса r окружности, вписанной в многоугольник со стороной а и числом сторон n: r=a/2tg(360°/2n). Площадь S вписанной в такой многоугольник окружности: S=π*(a/2tg(360°/2n)²/2.

Видео по теме

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?