Как найти площадь круга? Сначала найдите радиус. Учитесь решать простые и сложные задачи.
Содержание
- Площадь круга: формула через радиус, диаметр, длину окружности, примеры решения задач
- Формула нахождения площади круга через радиус:
- Формула нахождения S-площади круга через D-диаметр:
- Нахождение S круга, если известна длина окружности:
- Площадь круга, вписанного в квадрат: формула, примеры решения задач
- Задача №1: Известна сторона квадратной фигуры, которая равна 6 сантиметров. Найдите S-площадь вписанной окружности.
- Задача №2: Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см.
- Площадь круга, описанного около квадрата: формула, примеры решения задач
- Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: формула, примеры решения задач
- Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач
- Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач
- Площадь круга, описанного около прямоугольной и равнобедренной трапеции: формула, примеры решения задач
- Видео: Математика | Вычисление площадей круга и его частей
Круг — это замкнутая кривая. Любая точка на линии окружности будет находиться на одинаковом расстоянии от центральной точки. Круг — это плоская фигура, поэтому решать задачи с нахождением площади просто. В этой статье мы рассмотрим, как найти площадь круга, вписанного в треугольник, трапецию, квадрат, и описанного около этих фигур.
Площадь круга: формула через радиус, диаметр, длину окружности, примеры решения задач
Чтобы найти площадь данной фигуры, нужно знать, что такое радиус, диаметр и число π.
Радиус R — это расстояние, ограниченное центром окружности. Длины всех R-радиусов одной окружности будут равными.
Диаметр D — это линия между двумя любыми точками окружности, которая проходит через центральную точку. Длина этого отрезка равна длине R-радиуса, умноженной на 2.
Число π — это неизменная величина, которая равна 3,1415926. В математике обычно это число округляется до 3,14.
Формула нахождения площади круга через радиус:
Примеры решения заданий по нахождению S-площади круга через R-радиус:
————————————————————————————————————————
Задача: Найдите площадь окружности, если ее радиус равен 7 см.
Решение: S=πR², S=3,14*7², S=3,14*49=153,86 см².
Ответ: Площадь окружности равна 153,86 см².
Формула нахождения S-площади круга через D-диаметр:
Примеры решения заданий по нахождению S, если известен D:
————————————————————————————————————————-
Задача: Найдите S круга, если его D равен 10 см.
Решение: P=π*d²/4, P=3,14*10²/4=3,14*100/4=314/4=78,5 см².
Ответ: Площадь плоской круглой фигуры равна 78,5 см².
Нахождение S круга, если известна длина окружности:
Сначала находим, чему равен радиус. Длина окружности рассчитывается по формуле: L=2πR, соответственно радиус R будет равен L/2π. Теперь находим площадь круга по формуле через R.
Рассмотрим решение на примере задачи:
———————————————————————————————————————-
Задача: Найдите площадь круга, если известна длина окружности L — 12 см.
Решение: Сначала находим радиус: R=L/2π=12/2*3,14=12/6,28=1,91.
Теперь находим площадь через радиус: S=πR²=3,14*1,91²=3,14*3,65=11,46 см².
Ответ: Площадь круга равна 11,46 см².
Площадь круга, вписанного в квадрат: формула, примеры решения задач
Найти площадь круга, вписанного в квадрат просто. Сторона квадрата — это диаметр круга. Чтобы найти радиус, нужно сторону разделить на 2.
Формула нахождения площади круга, вписанного в квадрат:
Примеры решения задач по нахождению площади круга, вписанного в квадрат:
———————————————————————————————————————
Задача №1: Известна сторона квадратной фигуры, которая равна 6 сантиметров. Найдите S-площадь вписанной окружности.
Решение: S=π(a/2)²=3,14(6/2)²=3,14*9=28,26 см².
Ответ: Площадь плоской круглой фигуры равна 28,26 см².
————————————————————————————————————————
Задача №2: Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см.
Решайте так: Сначала найдем R=a/2=4/2=2 см.
Теперь найдем площадь окружности S=3,14*2²=3,14*4=12,56 см².
Ответ: Площадь плоской круглой фигуры равна 12,56 см².
Площадь круга, описанного около квадрата: формула, примеры решения задач
Немного сложнее находить площадь круглой фигуры, описанной около квадрата. Но, зная формулу, можно быстро подсчитать данное значение.
Формула нахождения S круга, описанного около квадратной фигуры:
Примеры решения заданий по нахождению площади окружности, описанной около квадратной фигуры:
Задача
Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: формула, примеры решения задач
Окружность, которая вписана в треугольную фигуру — это круг, который касается всех трех сторон треугольника. В любую треугольную фигуру можно вписать круг, но только один. Центром круга будет точка пересечения биссектрис углов треугольника.
Формула нахождения площади круга, вписанного в равнобедренный треугольник:
Когда будет известен радиус, площадь можно вычислить по формуле: S=πR².
Формула нахождения площади круга, вписанного в прямоугольный треугольник:
Примеры решения заданий:
Задача №1
Если в этой задаче нужно найти еще и площадь круга с радиусом 4 см, то сделать это можно по формуле: S=πR²
Задача №2
Решение:
Теперь, когда известен радиус, можно найти площадь круга через радиус. Формулу смотрите выше по тексту.
Задача №3
Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач
Все формулы по нахождению площади круга сводятся к тому, что сначала нужно найти его радиус. Когда известен радиус, то найти площадь просто, как было описано выше.
Площадь круга, описанного около прямоугольного и равнобедренного треугольника находится по такой формуле:
Примеры решения задач:
Вот еще пример решения задачи с использованием формулы Герона.
Решать подобные задачи сложно, но их можно осилить, если знать все формулы. Такие задачи школьники решают в 9 классе.
Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач
У равнобедренной трапеции две стороны равны. У прямоугольной трапеции один угол равен 90º. Рассмотрим, как найти площадь круга, вписанного в прямоугольную и равнобедренную трапецию на примере решения задач.
Например, в равнобедренную трапецию вписана окружность, которая в точке касания делит одну сторону на отрезки m и n.
Для решения этой задачи нужно использовать такие формулы:
Нахождение площади окружности, вписанной в прямоугольную трапецию, производится по следующей формуле:
Если известна боковая сторона, то можно найти радиус через это значение. Высота боковой стороны трапеции равна диаметру окружности, а радиус — это половина диаметра. Соответственно, радиус равен R=d/2.
Примеры решения задач:
Площадь круга, описанного около прямоугольной и равнобедренной трапеции: формула, примеры решения задач
Трапецию можно вписать в окружность, когда сумма ее противолежащих углов равна 180º. Поэтому вписать можно только равнобокую трапецию. Радиус для вычисления площадь круга, описанного около прямоугольной или равнобедренной трапеции, рассчитывается по таким формулам:
Примеры решения задач:
Решение: Большое основание в данном случае проходит через центр, так как в окружность вписана равнобедренная трапеция. Центр делит это основание ровно пополам. Если основание АВ равно 12, тогда радиус R можно найти так: R=12/2=6.
Ответ: Радиус равен 6.
В геометрии важно знать формулы. Но все их невозможно запомнить, поэтому даже на многих экзаменах разрешается пользоваться специальным формуляром. Однако важно уметь находить правильную формулу для решения той или иной задачи. Тренируйтесь в решении разных задач на нахождение радиуса и площади окружности, чтобы уметь правильно подставлять формулы и получать точные ответы.
Видео: Математика | Вычисление площадей круга и его частей
Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
Given a semicircle with radius R, which inscribes a rectangle of length L and breadth B, which in turn inscribes a circle of radius r. The task is to find the area of the circle with radius r.
Examples:
Input : R = 2 Output : 1.57 Input : R = 5 Output : 9.8125
Approach:
We know the biggest rectangle that can be inscribed within the semicircle has, length, l=√2R/2 &
breadth, b=R/√2(Please refer)
Also, the biggest circle that can be inscribed within the rectangle has radius, r=b/2=R/2√2(Please refer)
So area of the circle, A=π*r^2=π(R/2√2)^2
C++
#include <bits/stdc++.h>
using namespace std;
float area(float r)
{
if (r < 0)
return -1;
float area = 3.14 * pow(r / (2 * sqrt(2)), 2);
return area;
}
int main()
{
float a = 5;
cout << area(a) << endl;
return 0;
}
Java
import java.io.*;
class GFG {
static float area(float r)
{
if (r < 0)
return -1;
float area = (float)(3.14 * Math.pow(r / (2 * Math.sqrt(2)), 2));
return area;
}
public static void main (String[] args) {
float a = 5;
System.out.println( area(a));
}
}
Python3
from math import pow, sqrt
def area(r):
if (r < 0):
return -1
area = 3.14 * pow(r / (2 * sqrt(2)), 2);
return area;
if __name__ == '__main__':
a = 5
print("{0:.6}".format(area(a)))
C#
using System;
class GFG
{
static float area(float r)
{
if (r < 0)
return -1;
float area = (float)(3.14 * Math.Pow(r /
(2 * Math.Sqrt(2)), 2));
return area;
}
static public void Main (String []args)
{
float a = 5;
Console.WriteLine(area(a));
}
}
PHP
<?php
function area($r)
{
if ($r < 0)
return -1;
$area = 3.14 * pow($r /
(2 * sqrt(2)), 2);
return $area;
}
$a = 5;
echo area($a);
Javascript
<script>
function area(r)
{
if (r < 0)
return -1;
var area = (3.14 * Math.pow(r / (2 * Math.sqrt(2)), 2));
return area;
}
var a = 5;
document.write( area(a).toFixed(6));
</script>
Time Complexity: O(1)
Auxiliary Space: O(1)
Last Updated :
07 Aug, 2022
Like Article
Save Article
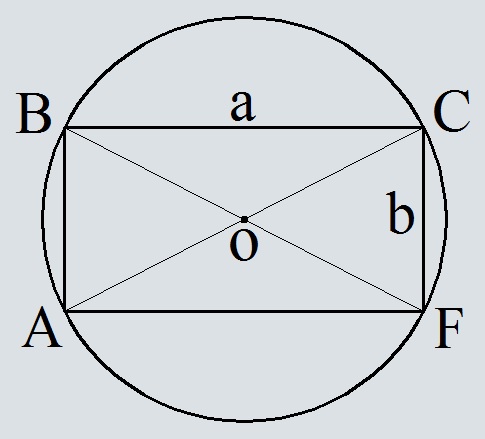
Расчёт площади круга описанного около прямоугольника, вычисленная по сторонам прямоугольника
Калькулятор рассчитывает площадь круга описанного около прямоугольника, вычисленная по сторонам прямоугольника.
Введите сторону a
Введите сторону b
Формула площади круга описанного около прямоугольника, вычисленная по сторонам прямоугольника
Где a, b – стороны прямоугольника,
π=3.14
Вывод формулы площади круга описанного около прямоугольника, вычисленная по сторонам прямоугольника
Диагонали прямоугольника пересекаются в центре окружности. Соответственно диагональ равна диаметру.
AC=BF=D
Из треугольника BCF по теореме пифагора вычислим BF=D по катетам BC=a и CF=b.
Подставим полученный диаметр в формулу площади окружности
Похожие калькуляторы
|
Несложная задача,вперед! Задачи подобного типа решаются следующим образом:
S/pi = 19/4 = 4 3/4 = 4,75 – я не знаю, какую форму записи требуют в ответе, поэтому привожу три варианта. Знаете ответ? |
Смотрите также: Что такое равновеликие фигуры (куб, квадрат, многоугольник)? Для чего нужна математика, геометрия, физика в программировании? Как найти вписанный угол ACB, если дуга BC составляет 80 градусов? Как найти длину отрезка BD, если SO = 35, SD = 37? Как найти величину угла OAB, если угол OCD равен 30 градусам? По каким учебникам изучают математику израильские школьники? Как решить: В четырехугольнике АВСD противоположные стороны не параллельны? Диагональ АС параллелограмма АВСD 21, от верш. В до диаг. 12. Чему равна S? Как найти площадь треугольника ABM (см.)? В угол с вершиной D вписана окружность с центром O, которая касается…? |
Площадь круга
Площадь круга радиуса $R$ равна $S = pi cdot R^2$. Убедимся в этом, воспользовавшись умением вычислять площадь прямоугольника и площадь треугольника.
Разделим круг диаметром на две половины. Каждую из них разобьём на одинаковые сектора. «Раскрыв» половины и вставив их одна в другую, получим фигуру, по площади равную площади изначального круга.
Эта фигура — почти прямоугольник. Почти — потому что длинные стороны не совсем прямые. Длина этих сторон равна половине длины окружности, т.е. $pi cdot R$.
А длина короткой стороны получившейся фигуры — в точности радиус изначальной окружности. Площадь прямоугольника вычисляется перемножением длин его сторон:
$S≈(pi cdot R)cdot R = pi cdot R^2$.
Использована формула для площади прямоугольника, однако получившаяся фигура — не совсем прямоугольник, поэтому и был написан знак приближённого равенства.
При этом понятно, что если круг делить на большее количество одинаковых частей, то отличие от прямоугольника будет всё меньше и меньше. В пределе, фигура не будет отличаться от
прямоугольника, а значит, такая модель не только наглядна, но и вполне законна.
Модель можно изготовить из дерева и полоски кожи. Кожу стоит подбирать отличного от дерева цвета, чтобы явно выделялась окружность в круге и длинные стороны в почти прямоугольнике.
В одной из половинок круга один из секторов стоит разбить на две части — так, чтобы внешние детали были половинками стандартных секторов.
Тогда получившаяся после сложения фигура будет больше походить на прямоугольник. В противном случае — на параллелограмм.
Чтобы воспользоваться формулой площади треугольника соберём круг из концентрически расположенных полосок, например, кожи. Внешняя должна быть самой длинной, следующая чуть короче и т.д.
Длину стоит подбирать так, чтобы при сгибании получался круг. На одном из радиусов сходятся концы полосок.
Развернём одновременно все полоски и круг превратится в почти треугольник. «Почти», потому что боковые стороны — не прямые линии, а состоят из ступенек.
В школе проходится несколько формул для вычисления площади треугольника (и все они дают одинаковый результат!).
Воспользуемся одной из них — площадь треугольника равна половине произведения длины стороны (например, основания) на длину высоты, проведенной к этой стороне.
Длина основания в нашем случае равна в точности длине окружности изначального круга, т.е. $2 cdot pi cdot R$.
А длина высоты есть просто радиус круга. Таким образом площадь получившейся фигуры $S ≈ (1/2) cdot (2 cdot pi cdot R) cdot R ≈ pi cdot R^2$.
Использована формула для площади треугольника, однако получившаяся фигура — не совсем треугольник, поэтому и был написан знак приближённого равенства.
При этом понятно, что если круг делать из всё более тонких полосок, то ступеньки на боковых сторонах будут всё меньше.
И в пределе, фигура не будет отличаться от треугольника, а значит, такое рассуждение вполне законно.