Как найти площадь круга зная его диаметр

Как найти площадь круга зная его диаметр

Площадь круга через Диаметр

S – площадь круга,

d – диаметр круга,

π ≈ 3,141592653589

Площадь круга через Радиус

S – площадь круга,

r – радиус круга,

π ≈ 3,141592653589

Площадь круга через Длину Окружности

S – площадь круга,

l – длина окружности,

π ≈ 3,141592653589

Определения и термины

Круг – множество точек плоскости, расстояние до которых от данной точки (центра круга) не превышает заданного расстояния (радиуса круга).

Радиус круга – отрезок, соединяющий центр круга с любой точкой, которая лежит на внешней окружности круг

Диаметр круга – отрезок, соединяющий любые две точки, лежащие на внешней окружности круга, и проходящий через центр круга

Окружность – замкнутая плоская кривая состоящия из всех точек полскости равноудаленных от заданной точки (центра окружности)

Число Пи (π) – математическая константа, которая выражает отношение длины окружности к её диаметру.
Равно приблизительно 3,141592653589…

Площадь окружности

Окружность, по своей сути, является границей круга – замкнутой плоской кривой. Из определения следует, что площади окружности не существует,
а существует Площадь круга.

Источник

Оглавление:

  • 📝 Как это работает?
  • 🤔 Частые вопросы и ответы
  • 📋 Похожие материалы
  • 📢 Поделиться и комментировать

Формула (формулы) площади круга

Найти площадь круга можно разными способами, в зависимости от известных данных.

По радиусу

Если дан только радиус, то площадь составит произведение константы Пи на квадрат радиуса. Расчёт будет по формуле (где r – радиус, а π – константа, равная 3,1415…):

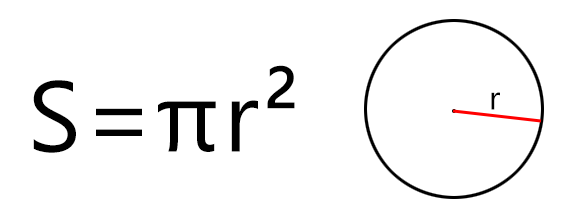
Формула площади круга по радиусу

Например, если радиус равен 2 метра, то площадь круг можно вычислить так S = 3,14 × 22 = 3,14 × 4 = 12,56 м2 (квадратных метров).

Через диаметр

Если известен диаметр, то площадь круга будет равняться одной четвёртой произведения Пи и квадрата диаметра. Формула площади круга будет такой (где d – диаметр, а π – константа, равная 3,1415…):

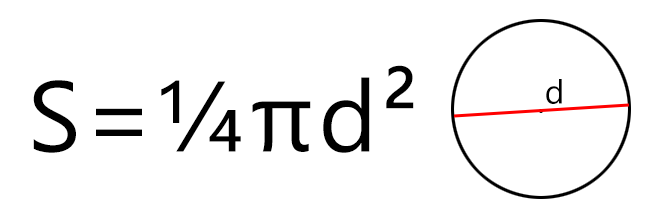
Формула площади круга по диаметру

К примеру, если диаметр круга (площадь поверхности пиццы) составляет 35 сантиметров, то площадь такого круга будет равна S = ¼ × 3,14 × 352 = ¼ × 3,14 × 1225 = 962 см2 (квадратных сантиметра).

Через длину окружности

Если мы знаем только длину окружности (периметр круга), то рассчитать площадь фигуры можно по формуле (где L – длина окружности, а π – константа, равная 3,1415…):

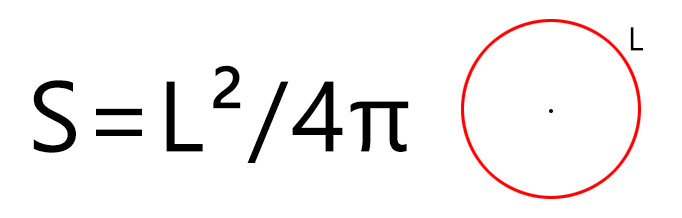
Формула площади круга по длине окружности

Например, если длинна окружности составляет 120 мм, тогда площадь круга будет равна S = 1202  / (4 × 3,14) = 14 400 / (4 × 3,14) = 1146,5 мм2 (квадратных миллиметров).

Какие термины используются для поиска площади круга?

Для вычисления площади круга, в формулах были использованы следующие термины, значение которых нужно знать, чтобы точно понимать принципы расчета.

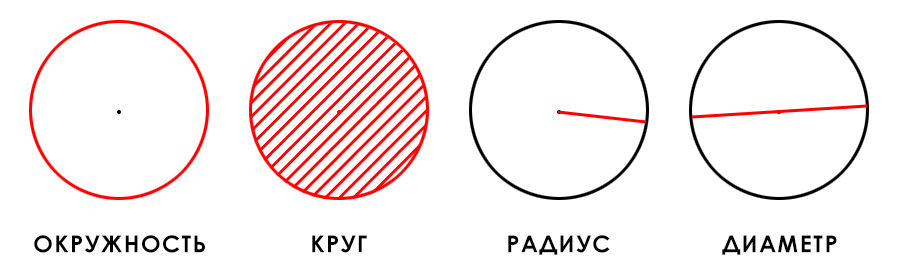
Окружность, круг, радиус, диаметр

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.

Диаметр — отрезок, соединяющий две точки на окружности и проходящий через центр окружности. Диаметр равен двум радиусам.

Радиус — отрезок, который соединяет центр окружности и любую точку на ней. 

Число π (пи) — математическая постоянная, равная отношению длины окружности к её диаметру. Пи равняется примерно 3,14.

Площадь круга и размеры пицц

Люди не всегда верно сопоставляют площадь круга и диаметры. К примеру, сможете ли вы ответить:

Площадь круга и размеры пицц

Что больше: 2 пиццы диаметром 25 см или 1 пицца диаметром 40 см?

Интуитивно кажется, что 2 пиццы, так как в сумме их радиусы дают 50 сантиметров, что больше, чем 40. Однако это неправильный вывод, так как сравнивать нужно не сумму диаметров, а сумму квадратов диаметров. То есть:

  • 252 + 252 = 625 + 625 = 1250
  • 402 = 1600

Так как ¼π является константой, то можно сравнивать только квадраты диаметров. Получается, что пицца 40 см больше, чем даже 2 пиццы размером 25 см. А вот если диаметр пиццы составляет 35 см, то 352 = 1225, и в этом случае 2 пиццы по 25 см будут иметь бОльшую площадь.

Площади усеченных частей круга

А также полезно знать следующие геометрические элементы, связанные с кругами и окружностями:

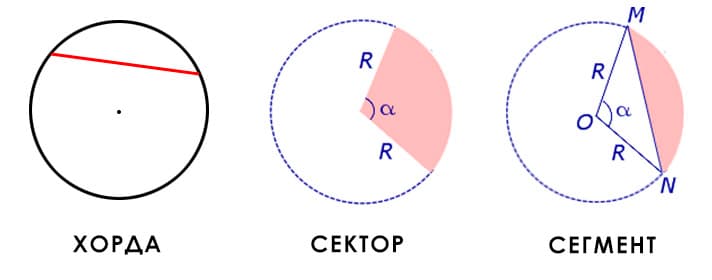
Хорда, сектор, сегмент и их площади

Хорда — отрезок, соединяющий любые две точки окружности.

Сектор — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Сектор является частью круга, а его площадь относится к площади круга так же, как и длина окружности сектора к длине всей окружности. Поэтому площадь сектора равна площади круга, умноженной на отношение длинны окружности сектора к длине окружности всего круга.

Но площадь сектора можно вычислить и по более простой формуле. Она равна длине дуги сектора, умноженной на половину радиуса:

S = sr/2

где S — площадь сектора, r — радиус круга.

Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой.

Площадь сегмента можно найти по формулам:

S = r2sinα/ 2

где S — площадь сегмента, sinα — синус угла двух между радиусов до концов хорды, r — радиус круга.

Часто задаваемые вопросы о площади круга?

И конечно, стоит ответить на некоторые вопросы, которые возникают во время расчетов.

Входит ли окружность (периметр) в площадь круга?

Да, входит, ведь кругом являются все точки, удаленные от центра круга на расстояние, которое не превышает радиус.

Какие есть ещё калькуляторы для круга у вас на сайте?

У нас есть разнообразные калькуляторы, в частности калькуляторы: длины окружности, диаметра и площади круга. Для последней калькулятор находится на данной странице.

Хватит ли только диаметра, только радиуса или только длинны окружности для расчета площади круга?

Да, хватит чего-то одного, так как все 3 сущности можно вывести одну из другой, например, диаметр равен двум радиусам, а длина окружности – это диаметр, умноженный на число Пи.

Почему Пи равняется 3,1415926…, а не является «ровным» числом?

Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.

Кто впервые научился вычислять площадь круга?

Гиппократ Хиосский (не тот, в честь которого назвали клятву) первым сформулировал, что площадь круга пропорциональна квадрату его диаметра. Евдокс Книдский в IV веке до н. э. строго доказал это утверждение. А Архимед в III веке до н. э. нашёл число Пи и продемонстрировал, что оно чуть меньше, чем 3 и 1/7.

Похожие калькуляторы

Возможно вам пригодятся ещё несколько калькуляторов по данной теме:

  • Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
  • Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
  • Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
  • Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
  • Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
  • Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
  • Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
  • Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
  • Калькулятор объема пирамиды. Рассчитайте объем пирамиды по высоте, площади основания или стороне основания. Основание может быть любой формы.
  • Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.

Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!

Есть что добавить?

Напишите своё мнение, комментарий или предложение.

Показать комментарии

Источник

Как рассчитать площадь круга

На данной странице калькулятор поможет рассчитать площадь круга онлайн. Для расчета задайте радиус, диаметр или длину окружности.

Круг – множество точек плоскости, удаленных от заданной точки этой плоскости (центр круг) на расстояние, не превышающее заданное (радиус круга).

Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.

Через радиус

Площадь круга через радиус

Формула для нахождения площади круга через радиус:

π – константа равная (3.14); r – радиус круга.

Через диаметр

Площадь круга через диаметр

Формула для нахождения площади круга через диаметр:

π – константа равная (3.14); d – диаметр.

Через длину окружности

Площадь круга через длину окружности

Формула для нахождения площади круга через длину окружности:

π – константа равная (3.14); l – длина окружности.

Источник

Нужно найти площадь круга – как можно решить задачу и какие методы для этого использовать? Подробно рассмотрим эту тему и научимся без труда решать типовые задания по математике.

как найти площадь круга

Определения и основные понятия

Перед тем, как приступить к разбору формул и решению задач, нужно запомнить основные определения:

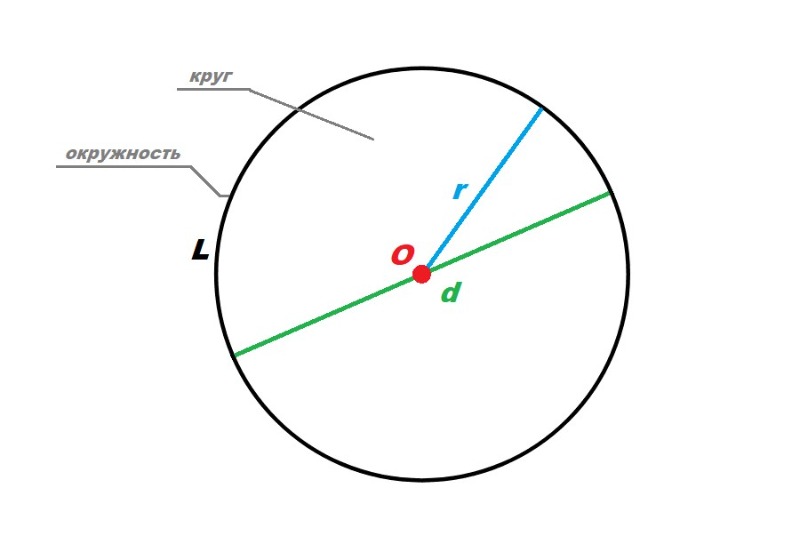
  • Круг – плоская геометрическая фигура, представляющая собой скопление точек в пределах окружности.
  • Окружность – замкнутая линия определенной длины (L), каждая из точек которой равномерно отдалена от центра (О).
  • Радиус (r) – расстояние от центра до окружности.
  • Диаметр (d) – линия, соединяющая две точки, расположенные на окружности, и пересекающая центр. При этом, d = 2*r.
  • π – константа, округленное значение которой равно 3,14.

Площадь круга через диаметр

Для нахождения площади круга можно использовать несколько методов в зависимости от того, о чем говорится в задании. Если мы знаем величину диаметра, то площадь можно найти по формуле S = d²:4*π. То есть диаметр нам нужно возвести в квадрат, а затем разделить получившееся значение на четыре и умножить на 3,14. 

Также этим методом можно воспользоваться, если известен радиус. Для этого требуется умножить его на два, в результате чего удастся узнать диаметр. После этого площадь можно будет найти по указанной ранее формуле.

найти площадь круга по формуле

Площадь круга через радиус и длину окружности

Найти площадь такой фигуры, как круг, можно и через радиус, если воспользоваться формулой S = π*r², то есть квадрат радиуса нужно умножить на число Пи. В этом случае диаметр искать не придется, а значит задачу можно будет решить более простым путем.

Еще один способ доступен, если известна длина окружности. Ее требуется возвести в квадрат и разделить на произведение четырех и числа Пи: S = L​²:(4*π). 

Задачи для тренировки

Теперь, когда основные формулы уже рассмотрены, стоит закрепить свои знания на примере задач из школьной программы. Допустим, нам нужно найти S круга, если известно, что:

  • радиус равен 8 дм. В этом случае S = 3.14*8² = 200,96 дм².
  • диаметр равен 12 см. Вычисляем S = 12²:4*3,14 = 113,04 см².
  • длина окружности равна 16 м. То есть: S = 16​²:(4*3,14) = 20,38 м².

Тема, которую мы рассмотрели, не является сложной, особенно если тщательно ее разобрать. Это же касается и других тем по математике – важно своевременно закреплять свои знания, и тогда удастся преуспеть в изучении этого предмета. 

Уделять внимание математике нужно с первых лет обучения в школе, ведь именно в начальных классах ребенку прививаются важнейшие базовые знания и навыки. Развитие математических способностей в младшем возрасте создаст надежную основу для дальнейшего обучения.

Источник


Загрузить PDF


Загрузить PDF

Некоторые учащиеся не понимают, как найти площадь круга по исходным данным. Для начала нужно запомнить формулу, по которой вычисляется площадь круга: S=pi r^{2}. Формула проста: чтобы найти площадь круга, нужно знать только его радиус. Но нужно уметь преобразовывать другие исходные величины, чтобы воспользоваться этой формулой.

  1. Изображение с названием Calculate the Area of a Circle Step 1

    1

    Найдите радиус круга. Радиус – это отрезок, соединяющий центр круга с любой точкой внешней окружности круга. Радиус можно измерить в любом направлении: он будет одним и тем же. Радиус также равен половине диаметра круга. Диаметр – это отрезок, который проходит через центр круга и соединяет две точки внешней окружности круга.[1]

    • Как правило, значение радиуса дано в условиях задачи. Довольно трудно найти точный центр круга, если только он не обозначен на круге, который нарисован на бумаге.
    • Например, радиус круга равен 6 см.

  2. Изображение с названием Calculate the Area of a Circle Step 2

    2

    Возведите радиус в квадрат. Формула для вычисления площади круга: S=pi r^{2}, где r – радиус, который возведен во вторую степень (в квадрат).[2]

  3. Изображение с названием Calculate the Area of a Circle Step 3

    3

    Полученный результат умножьте на число Пи. Это число обозначается греческой буквой pi и представляет собой математическую константу, которая характеризует взаимосвязь радиуса и площади круга. Число Пи приблизительно равно 3,14. Точное значение числа Пи включает бесконечное количество цифр. Иногда ответ (площадь круга) записывается с постоянной pi .[3]

    • В нашем примере (r = 6 см) площадь вычисляется так:

  4. Изображение с названием Calculate the Area of a Circle Step 4

    4

    Запишите ответ. Помните, что площадь измеряется в квадратных единицах. Если радиус дан в сантиметрах, площадь измеряется в квадратных сантиметрах. Если радиус дан в миллиметрах, площадь измеряется в квадратных миллиметрах. Уточните у преподавателя, нужно ли представить ответ с постоянной pi или в числовой форме, используя приблизительное значение числа Пи. Если требование не ясно, запишите оба варианта ответа.[4]

    • В нашем примере (r = 6 см) S = 36pi см2 или S = 113,04 см2.

    Реклама

  1. Изображение с названием Calculate the Area of a Circle Step 5

    1

    Измерьте или запишите диаметр. В некоторых задачах радиус не дан. Вместо радиуса указывается диаметр. Если диаметр нарисован на бумаге, измерьте его с помощью линейки. Скорее всего, числовое значение диаметра будет задано.

    • Например, диаметр круга равен 20 мм.

  2. Изображение с названием Calculate the Area of a Circle Step 6

    2

    Разделите диаметр пополам. Помните, что диаметр равен удвоенному радиусу. Поэтому разделите любое значение диаметра на 2, чтобы найти радиус.

    • Таким образом, если диаметр круга равен 20 мм, то радиус круга равен 20/2 = 10 мм.

  3. Изображение с названием Calculate the Area of a Circle Step 7

    3

  4. Изображение с названием Calculate the Area of a Circle Step 8

    4

    Запишите ответ. Помните, что площадь измеряется в квадратных единицах. В нашем примере диаметр дан в миллиметрах, поэтому радиус тоже измеряется в миллиметрах, а площадь в квадратных миллиметрах. В нашем примере S = 100pi мм2.

    • Также ответ можно представить в численной форме, используя вместо pi приблизительное значение 3,14. В этом случае S = (100)(3,14) = 314 мм2.

    Реклама

  1. Изображение с названием Calculate the Area of a Circle Step 9

    1

    Запишите преобразованную формулу. Если известна длина окружности круга, можно воспользоваться преобразованной формулой для вычисления его площади. Такая формула включает длину окружности, а не радиус, и записывается так:

    • S={frac {C^{2}}{4pi }}

  2. Изображение с названием Calculate the Area of a Circle Step 10

    2

    Измерьте или запишите длину окружности. В некоторых ситуациях нельзя точно измерить диаметр или радиус. Если диаметр не нарисован или центр не отмечен, очень сложно найти точный центр круга. Длину окружности некоторых предметов (например, сковороды) довольно легко измерить с помощью рулетки, то есть можно найти более точное значение длины окружности, чем диаметра.[5]

    • Например, длина окружности круга (или круглого предмета) равна 42 см.

  3. Изображение с названием Calculate the Area of a Circle Step 11

    3

  4. Изображение с названием Calculate the Area of a Circle Step 12

    4

    Запишите формулу для вычисления площади круга. Запишите преобразованную формулу на основе соотношения между длиной окружности и радиусом. Подставьте последнее равенство в стандартную формулу для вычисления площади круга:[7]

  5. Изображение с названием Calculate the Area of a Circle Step 13

    5

    Воспользуйтесь преобразованной формулой, чтобы решить задачу. Теперь в формуле вместо радиуса присутствует длина окружности, поэтому можно вычислить площадь круга по известной длине окружности. Подставьте значение длины окружности и выполните вычисления следующим образом:[8]

  6. Изображение с названием Calculate the Area of a Circle Step 14

    6

    Запишите ответ. Если длина окружности дана в виде числа, а не произведения числа и pi , ответ можно записать с pi в знаменателе. Или вместо числа Пи подставьте его приблизительное значение (3,14).[9]

    Реклама

  1. Изображение с названием Calculate the Area of a Circle Step 15

    1

    Запишите известные величины. В некоторых задачах дана площадь сектора круга, по которой нужно найти площадь всего круга. Внимательно прочитайте такую задачу; ее условие может выглядеть так: «Площадь сектора круга равна 15pi см2. Найдите площадь всего круга».[10]

  2. Изображение с названием Calculate the Area of a Circle Step 16

    2

    Запомните определение сектора. Сектор круга – это часть круга, которая ограничена дугой и двумя радиусами. Пространство между такими радиусами и дугой называется сектором.[11]

  3. Изображение с названием Calculate the Area of a Circle Step 17

    3

    Измерьте центральный угол сектора. Воспользуйтесь транспортиром, чтобы измерить угол между двумя радиусами. Линейку (прямолинейную шкалу) совместите с одним из радиусов, причем центр линейки должен совпадать с центром круга. Затем найдите величину угла; для этого посмотрите на точку пересечения второго радиуса с угломерной шкалой.[12]

    • Не перепутайте внутренний и внешний угол между двумя радиусами. В задаче должно быть указано, с каким углом работать. Помните, что сумма внутреннего и внешнего углов равна 360 градусов.
    • Во многих задачах центральный угол дан, то есть измерять его не нужно. Например, в задаче может быть сказано: «Центральный угол сектора равен 45 градусов»; если это не так, измерьте центральный угол.

  4. Изображение с названием Calculate the Area of a Circle Step 18

    4

    Используйте преобразованную формулу для вычисления площади круга. Если известны площадь сектора и его центральный угол, используйте следующую преобразованную формулу, чтобы найти площадь круга: [13]

  5. Изображение с названием Calculate the Area of a Circle Step 19

    5

  6. Изображение с названием Calculate the Area of a Circle Step 20

    6

    Запишите ответ. В нашем примере сектор составлял одну восьмую полного круга. Поэтому площадь полного круга равна 120pi см2. Так как площадь сектора дана с постоянной pi , скорее всего, ответ тоже можно представить с этой постоянной.[15]

    • Чтобы записать ответ в численной форме, умножьте 120 x 3,14 = 376,8 см2.

    Реклама

Об этой статье

Эту страницу просматривали 264 783 раза.

Была ли эта статья полезной?

Источник

Добавить комментарий