В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь сектора круга, а также разберем примеры решения задач для демонстрации их практического применения.
- Определение сектора круга
-
Формулы нахождения площади сектора круга
- Через длину дуги и радиус круга
-
Через угол сектора (в градусах) и радиус круга
- Через угол сектора (в радианах) и радиус круга
- Примеры задач
Определение сектора круга
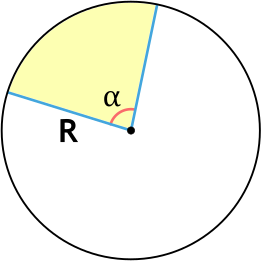
Сектор круга – это часть круга, образованная двумя его радиусами и дугой между ними. На рисунке ниже сектор закрашен зеленым цветом.
- AB – дуга сектора;
- R (или r) – радиус круга;
- α – это угол сектора, т.е. угол между двумя радиусами. Также его иногда называют центральным углом.
Формулы нахождения площади сектора круга
Через длину дуги и радиус круга
Площадь (S) сектора круга равняется одной второй произведения длины дуги сектора (L) и радиуса круга (r).
Через угол сектора (в градусах) и радиус круга
Площадь (S) сектора круга равняется площади круга, умноженной на угол сектора в градусах (α°) и деленной на 360°.
Через угол сектора (в радианах) и радиус круга
Площадь (S) сектора круга равняется половине произведения угла сектора в радианах (aрад) и квадрата радиуса круга.
Примеры задач
Задание 1
Дан круг радиусом 6 см. Найдите площадь сектора, если известно, что длина его дуги составляет 15 см.
Решение
Воспользуемся первой формулой, подставив в нее заданные значения:
Задание 2
Найдите угол сектора, если известно, что его площадь равна 78 см2, а радиус круга – 8 см.
Решение
Выведем формулу для нахождения центрального угла из второй формулы, рассмотренной выше:
Круговой сектор — часть круга, которая ограничена дугой этого самого круга и двумя радиусами.
Онлайн-калькулятор площади сектора круга
Возьмем две произвольные точки, лежащие на границе круге. Они делят ее на две разные части, которые могут быть как одинаковыми по длине, так и разными. Эти части называются дугами круга.
Дуги равны по длине, когда равны углы, с помощью которых они образованы.
Рассмотрим задачу о нахождении площади сектора круга.
Формула площади сектора круга по радиусу и длине дуги
S=12⋅r⋅lS=frac{1}{2}cdot rcdot l
rr — радиус круга;
ll — длина дуги.
Рассмотрим решение задачи.
Найдите площадь кругового сектора, если известно, что длина дуги равна 20 (см.), а радиус круга равен 5 (см.).
Решение
r=5r=5
l=20l=20
В данной задаче сразу можно подставить наши числа в исходную формулу и вычислить площадь:
S=12⋅r⋅l=12⋅5⋅20=50S=frac{1}{2}cdot rcdot l=frac{1}{2}cdot 5cdot 20=50 (см. кв.)
Ответ: 50 см. кв.
Формула площади сектора круга по радиусу и угла в радианах
S=12⋅r2⋅αS=frac{1}{2}cdot r^2cdot alpha
rr — радиус круга;
αalpha — центральный угол, измеряемый в радианах.
Пример решения задачи.
Найдите площадь кругового сектора, если радиус круга равен 8 (см.), а центральный угол кругового сектора равен π2frac{pi}{2} радиан.
Решение
r=8r=8
α=π2alpha=frac{pi}{2} рад.
По формуле получаем:
S=12⋅r2⋅α=12⋅82⋅π2≈50.2S=frac{1}{2}cdot r^2cdot alpha=frac{1}{2}cdot 8^2cdotfrac{pi}{2}approx50.2 (см. кв.)
Ответ: 50.2 см.кв.
Формула площади сектора круга по радиусу и углу в градусах
S=π360⋅r2⋅αS=frac{pi}{360}cdot r^2cdot alpha
rr — радиус круга;
αalpha — центральный угол, измеряемый в градусах.
Эту формулу можно получить используя связь между радианами и градусами:
2π рад.=360∘2pitext{ рад.}=360^{circ}
Найти площадь кругового сектора, если дан радиус круга равный 10 (см.), а центральный угол сектора равен 180180 градусов.
Решение
r=10r=10
α=180∘alpha=180^{circ}
Площадь данного сектора:
S=π360⋅r2⋅α=π360⋅102⋅180∘≈157S=frac{pi}{360}cdot r^2cdot alpha=frac{pi}{360}cdot 10^2cdot 180^{circ}approx157 (см. кв.)
Ответ: 157 см. кв.
Решение задач по геометрии онлайн от экспертов сайта Студворк!
Тест по теме “Площадь сектора круга”
Здесь вы можете рассчитать площадь сектора круга с помощью удобного онлайн калькулятора по двум формулам. Для этого необходимо ввести известные вам параметры фигуры:
- радиус круга и угол,
- длину дуги и радиус.
Сектор круга или окружности – это его(её) часть, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга (окружности).
Содержание:
- калькулятор площади сектора круга
- формула площади сектора круга через радиус и угол
- формула площади сектора круга через радиус и длину дуги
- примеры задач
Формула площади сектора круга через радиус и угол
S = pi R^2 dfrac{alpha °}{360°}
S = dfrac{alpha}{2} R^2
R – радиус сектора
α° – угол сектора (в градусах)
α – угол сектора (в радианах)
Формула площади сектора круга через радиус и длину дуги
S = dfrac{1}{2}LR
L – длина дуги сектора
R – радиус сектора
Примеры задач на нахождение площади сектора круга
Задача 1
Найдите площадь сектора круга радиуса 1 длина дуги которого равна 2.
Решение
Для решения задачи нам подойдет вторая формула.
S = dfrac{1}{2}LR = dfrac{1}{2} cdot 2 cdot 1 = dfrac{1}{2} cdot 2 = 1 : см^2
Ответ: 1 : см^2
Давайте проверим ответ с помощью калькулятора .
Задача 2
Найдите площадь сектора круга радиуса 24 длина дуги которого равна 3.
Решение
Задача аналогична предыдущей.
S = dfrac{1}{2}LR = dfrac{1}{2} cdot 3 cdot 24 = dfrac{1}{2} cdot 72 = 36 : см^2
Ответ: 36 : см^2
Проверка .
Задача 3
Найдите площадь кругового сектора если радиус круга равен 3, а угол сектора равен 120°.
Решение
Для решения этой задачи нам потребуется первая формула, в которой угол указывается в градусах.
S = pi R^2 dfrac{alpha °}{360°} = pi cdot 3^2 cdot dfrac{120°}{360°} = pi cdot 9 cdot dfrac{1}{3} = 3 pi : см^2 approx 9.42478 : см^2
Ответ: 3 pi : см^2 approx 9.42478 : см^2
Проверка .
Сектор круга ограничивается дугой между двумя точками A и B на окружности и двумя радиусами, проведенными из концов дуги (точек A и B) к центру круга. Два радиуса делят всю площадь круга на 2 сектора, если угол между радиусами будет развернутым (180 градусов), то эти секторы будут между собой равны. Площадь сектора круга – это часть S всей плоской фигуры, ограниченной окружностью с радиусом r.
Площадь круга равна произведению квадрата радиуса на число «пи».
Площадь сектора может быть выражена формулой S = π х r² х α/360. В ином виде при указании угла сектора α не в градусах, а в радианах, S = (α/2) х r². Расчет площади сектора круга можно также осуществить еще по одной формуле через длину секторной дуги.
В разделе представлены сразу три варианта формул онлайнового калькулятора. Работники конструкторских отделов, а также пока еще познающие основы конструирования сложного оборудования, обучающиеся в Вузах студенты, могут воспользоваться любым из них на свой выбор.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Как рассчитать площадь сектора круга
На данной странице калькулятор поможет рассчитать площадь сектора круга онлайн. Для расчета задайте радиус, длину дуги или угол сектора круга.
Сектор круга – это часть круга, окружности ограниченная дугой и двумя радиусами, проведенными к концам дуги.
Через длину дуги и радиус
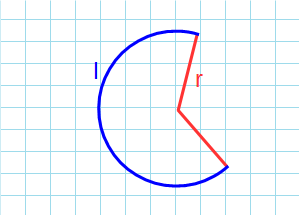
Формула для нахождения площади сектора круга:
l – длина дуги окружности; r – радиус окружности.
Через угол и радиус
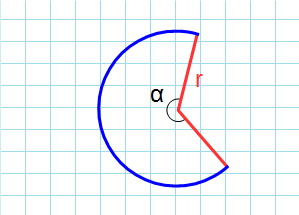
Формула для нахождения площади сектора круга:
— в градусах;
— в радианах;
π – константа равная (3.14); α – угол сектора круга; r – радиус окружности.