Как найти площадь купола формула

Enter the dome radius and the dome height into the Dome Surface Area Calculator. The calculator will evaluate the Dome Surface Area. 

• All Area Calculators
• Subwoofer Cone Area Calculator
• Area of an Oval Calculator
• Surface Area of a Pipe Calculator

Dome Surface Area Formula

The following two example problems outline the steps and information needed to calculate the Dome Surface Area.

• Where DSA is the Dome Surface Area
• r is the dome radius 
• h is the dome height 

To calculate dome surface area, multiply the radius by the the height, then multiply this result by 2 times pi.

How to Calculate Dome Surface Area?

The following example problems outline how to calculate Dome Surface Area.

Example Problem #1:

1. First, determine the dome radius. 
   • The dome radius is given as: 5.
2. Next, determine the dome height. 
   • The dome height is provided as: 3.
3. Finally, calculate the Dome Surface Area using the equation above: 

DSA = 2*pi*r*h =

The values provided above are inserted into the equation below and computed.

DSA = 2*pi*5*3 = 94.24

---

Example Problem #2: 

For this problem, the variables required are provided below:

dome radius = 6

dome height = 2

Test your knowledge using the equation and check your answer with the calculator..

DSA = 2*pi*r*h = ?

Площадь поверхности купола — это сумма площади боковой поверхности, образованной образующей сегмента, вращающегося вокруг оси, проходящей через одну вершину сегмента (под острым углом к диаметру основания сегмента), и площади основания.

Под куполом будем подразумевать тело, ограниченное образующей сегмента, вращающегося вокруг оси, проходящей через одну вершину сегмента (под острым углом к диаметру основания сегмента), и плоскостью перпендикулярной оси вращения.

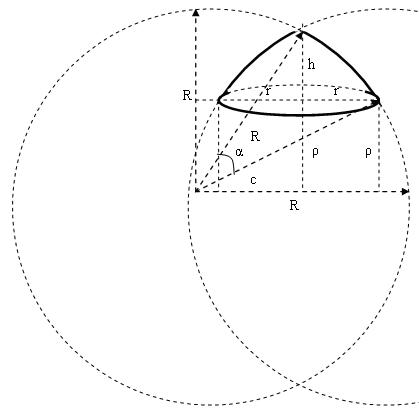
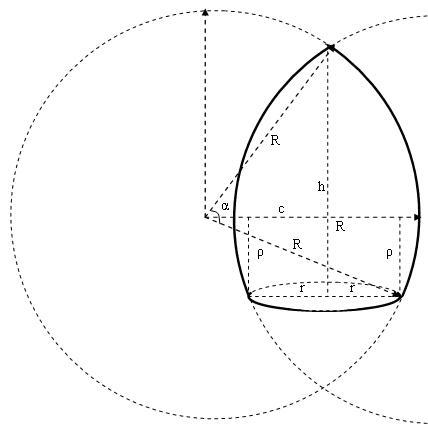
Обозначения

Введём обозначения:

R — радиус образующей дуги окружности;

r — радиус основания купола;

ρ — расстояние от основания купола до горизонтальной оси, проходящей через центр образующей окружности;

с — расстояние от центра образующей дуги окружности до вертикальной оси купола;

h — высота купола;

α — угол между радиусами образующей дуги окружности, соединяющими центр с краями образующего сегмента;

S_бок — площадь боковой поверхности купола.

S_осн — площадь основания купола.

S_куп — площадь поверхности купола.

Формула

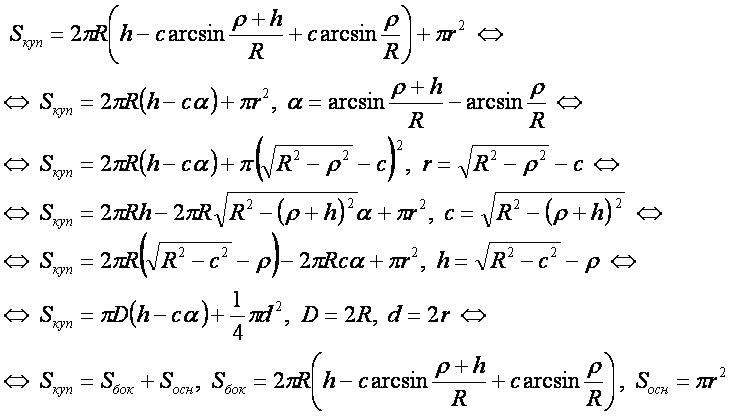
Вывод формулы

• Для вывода используется формула 1 “площадь поверхности фигуры вращения”.

Другие фигуры:

Ссылки

• Участник:Logic-samara

В 2021 году в сборнике типовых заданий ОГЭ по математике появилась новая задача про зонт.

Вот ее текст

По этому тексту, надо ответить на 5 вопросов, которые входят в первых 5 заданий ОГЭ по математике.

Вопрос №1.

Длина зонта в сложенном виде равна 25 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,3 см.

Для ответа на этот вопрос. можно начертить схему, в виде отрезка, который разбит на две части, одна часть – это ручка, вторая это 1/3 часть длины спицы.

Первым действием, мы находим, сколько сантиметров, составляет 1/3 длины спицы.

Вторым действием, умножаем на 3, и получаем искомую длину спицы, которую нужно будет внести в бланк ответов.

Обратная задача из репетиционного экзамена от 28.01.2022 года:

Длина одной спицы у раскрытого зонта равна 69,6 см. При закрытии зонта спицы одновременно складываются. Длина зонта в сложенном виде равна 24,9 см, длина ручки равна 7,5 см. Во сколько раз складывается каждая спица?

Решение:

1) 24,9-7,5=17,4 (длина спицы в сложенном виде)

2)69,6:17,4=4 (в 4 раза складывается каждая спица)

Ответ 4

Вопрос №2.

Поскольку зонт сшит из треугольников, рассуждала Нина, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Нины, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 54,2 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.

При ответе на этот вопрос, обратимся к тексту задачи, и найдем чему, равно основание равнобедренного треугольника а=38 см

Первым действием, мы найдем площадь равнобедренного треугольника, которая равна: половине произведения высоты на сторону к которой эта высота проведена.

Вторым действием, найдем площадь поверхности зонта. Для этого нужно площадь одного треугольника, умножить на количество треугольников из которых сшит зонт, оно равно 8 (написано в третьем предложении текста задачи). В ответе записываем значение. округленное до разряда десятков т.е. 8240.

Вопрос №3

Света предположила, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что OC=R. Ответ дайте в сантиметрах.

В этой задаче, на рисунке нужно было выделить прямоугольный треугольник (в нашем случае, мы его назвали ОКD), и по теореме Пифагора, 1) составили выражение, для нахождения радиуса сферы. 2) выразили из отрезка ОС и СК отрезок ОК. 3) Нашли значение КD, оно равно половине d=104, поскольку О – это центр окружности. 4) Подставили в формулу 1, и с помощью формулы сокращенного умножения, раскрыли скобку, и нашли значение R=65. Этот ответ записываем в бланк ответов.

Задача №4

Света нашла площадь купола зонта как площадь поверхности сферического сегмента по формуле S=2пRh , где R – радиус сферы, а h – высота сегмента. Рассчитайте площадь поверхности купола способом Светы. Число п -“пи” округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.

Эта задача самая простая, если вы правильно рассчитали радиус сферы R в третьем задании. Нужно только все подставить в формулу, и посчитать.

Задача №5

Рулон ткани имеет длину 24 м и ширину 150 см. На фабрике из этого рулона были вырезаны треугольные клинья для 36 зонтов, таких же, как зонт, который был у Нины и Светы. Каждый треугольник с учётом припуска на швы имеет площадь 1100 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?

При внимательном прочтении задачи, понимаем, что нужно найти площадь ткани в рулоне, затем площадь материала, которое потребовалось для 36 зонтов. И найти сколько ушло ткани в обрезки.

Решение ниже:

1) Найдем площадь ткани в рулоне.

2) Найдем количество клиньев треугольников, которые вырезали из рулона ткани для 36 зонтиков. в каждом по 8 треугольников.

3) Находим сколько материала потребовалось на 288 треугольников.

4) Находим сколько материала ушло в обрезки.

5) Находим отношение между обрезками и всего материалом, составив пропорцию.

В комментариях напишите, какая из задач такого вида, для вас самая легкая, а какая сложная?

Спасибо, что прочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.

Геодезический купол. Об устройстве и моем опыте расчетов

Немного истории

Геодезические купола — архитектурные сооружения с несущей сетчатой оболочкой впервые появились в конце 40-х годов прошлого века. Патент на это изобретение получил американец Ричард Фуллер. Необычные строения должны были решить проблему быстрого возведения недорогого комфортабельного жилья. Для массовой застройки идея не прижилась, но активно используется для строительства футуристических кафе, бассейнов, стадионов.

Не менее популярны сферы и среди ландшафтных дизайнеров. Такие строения достаточно просторны и могут быть использованы для самых разных целей. Их необычный вид сразу притягивает внимание, они становятся центром пейзажной композиции.

Геодезический купол обладает большой несущей способностью, к тому же его можно построить из простых материалов в самые короткие сроки без привлечения бригад специалистов и техники. Так, купол высотой в 50 метров можно построить силами трех человек без привлечения строительного крана.

Как правильно производить расчет длин стропильных частей?

Обязательно обратите внимание, при пользовании калькулятором, на то, что использование коннектора другого вида, который отличается от представленного в видеоролике, может повлечь за собой необходимость в изготовлении стропильных частей других длин.

Всё будет зависеть от того, какое расстояние между болтовыми соединениями стропильных частей, исходя из этого, уже и следует производить правильный расчет длины.

Также обратите внимание и на то, что коннекторы могут быть пятилучевыми или шестилучевыми, все зависит от места их размещения в конструкции самого каркаса купольного дома и от того, сколько стропил, они будут соединять.

На въезде вашей территории загородного дома мы рекомендуем установить ворота с автоматикой и аксессуарами безопасности. Такими автоматическими воротами будет не только комфортно управлять, но и совершенно безопасно.

Рейтинг блогов и записей Живого Журнала

Расчет геодезического купола производится по заданному радиусу (площади поверхности основания), с целью получить:

• Расчетные размеры ребер и их количество
• Количество и тип требуемых коннекторов
• Значения углов между ребрами
• Требуемые высоту, общую площадь постройки
• Площадь поверхности купола

Площадь основания купола ассчитывается по заданному радиусу S=π *R2. При этом надо учитывать, что реальная площадь получится несколько меньше, вследствие того, что радиус купола считается, обычно, по внешней поверхности полусферы (по «вершинам»), и стенки купола имеют также определенную толщину.

Геодезический купол — не чистая сфера, апроксимация приводит к тому, что в основании лежит не круг, а многоугольник, вписанный в заданную окружность. Площадь такого многоугольника заведомо меньше площади круга.

Высота геодезического купола пределяется по заданному диаметру, и может быть для четной частоты разбиения 1/2, 1/4 диаметра (при большой частоте может быть и 1/6, 1/8). Для нечетной — 3/8, 5/8 диаметра (и т.д.).

4V, 1/4 сферы

4V, 1/2 сферы

Площадь поверхности геодезического купола ассчитывается по известной формуле расчета площади сферы S=4π *R2. Для купола, равного 1/2 сферы, формула будет иметь вид S=2π *R2. В более сложному случае, когда речь идет о площади сегмента, сферы, формула расчета S=2π *RH, где H — высота сегмента.
Расчет конструктивных элементов геодезического купола ожно производить с использованием готовых таблиц, в которых заданы:

1. Количество ребер купола одинаковой длины — ребра A, B, C, D, E, F, G, H, I. У купола с частотой 1V одно ребро — A. У купола с частотой 2V два ребра — A, B. У купола с частотой 3V три ребра — A, B, C. И т.д.
2. Количство и тип используемых коннекторов — 4-х конечные, 5-ти конечные, 6-ти конечные.
3. Коэффициенты пересчета длин ребер купола на радиус купола. К примеру, если вы хотите построить купол с частотой 2V высотой 1/2 и радиусом 3,5 метра, вам надо величину радиуса (3,5) умножить на коэффициент 0,61803 для определения длины ребра А, и умножить на коэффициент 0,54653 для определения длины ребра B. Получим: А=2,163м, В=1,912м.

1V купол

Ребра	Коэффициенты	Количество
A	1.05146	25
5-ти конечный коннектор	6
4-х конечный коннектор	5

2V купол

Ребра	Коэффициенты	Количество для 1/2
A	0,61803	35
B	0,54653	30
4-х конечный коннектор	10
5-ти конечный коннектор	6
6-ти конечный коннектор	10

3V купол

Ребра	Коэффициенты	Количество для 3/8	Количество для 5/8
A	0,34862	30	30
B	0,40355	40	55
C	0,41241	50	80
4-х конечный коннектор	15	15
5-ти конечный коннектор	6	6
6-ти конечный коннектор	25	40

4V купол

Ребра	Коэффициенты	Количество для 1/2
A	0,25318	30
B	0,29524	30
C	0,29453	60
D	0,31287	70
E	0,32492	30
F	0,29859	30
4-х конечный коннектор	20
5-ти конечный коннектор	6
6-ти конечный коннектор	65

5V купол

Ребра	Коэффициенты	Количество для 5/8
A	0,19814743	30
B	0,23179025	30
C	0,22568578	60
D	0,24724291	60
E	0,25516701	70
F	0,24508578	90
G	0,26159810	40
H	0,23159760	30
I	0,24534642	20
4-х конечный коннектор	25
5-ти конечный коннектор	6
6-ти конечный коннектор	120

6V купол

Ребра	Коэффициенты	Количество для 1/2
A	0,1625672	30
B	0,1904769	30
C	0,1819083	60
D	0,2028197	90
E	0,1873834	30
F	0,1980126	60
G	0,2059077	130
H	0,2153537	65
I	0,2166282	60
4-х конечный коннектор	30
5-ти конечный коннектор	6
6-ти конечный коннектор	160

Углы между ребрами между «лепестками» коннекторов) легко вычисляются по заданным сторонам треугольников.

Приблизительные значения углов апроксимации, в которых сходятся ребра геодезического купола на его вершинах:

• 1V купол — А=32º
• 2V купол — A=18º, B=16º
• 3V купол — A=10º, B=12º, С=12º
• 4V купол — A, B, С, D, E, F — 7-9º
• 5V купол — A, B, С, D, E, F, G, H, I — 6-7º
• 6V купол — A, B, С, D, E, F, G, H, I — 5-6º

Калькуляторы on-line:

Acidome calculator толковый российский on-line калькулятор

Geo-Dome
Tags: купол

Купольные дома: примеры и обзор технологий строительства

В представлении большинства людей жилой дом – прямоугольная коробка под скатной крышей.

К конструкциям сферического и купольного очертания отношение двоякое. Привлекая внимание необычным «космическим» видом у многих они вызывают сомнения в надежности и удобстве проживания.

Преодолеть сложившийся «кубический» стереотип, объективно изучить достоинства и недостатки купольных домов, оценить возможность их самостоятельного строительства вам поможет эта статья.

Дом сфера – прихоть архитектора или подсказка природы?

Начнем с того, что многие выдающиеся изобретения человек позаимствовал у природы, наблюдая за жизнью животных. Давайте обратим внимание на «технологии», используемые птицами при строительстве своих жилищ. Нетрудно заметить, что здесь нигде нет прямых углов. Полусферы, шары, окружности – только такие формы признает природа. Получается, что столь любимая нами жилая «коробка» вовсе не является венцом творения.

Обратив внимание на этот природный феномен, инженеры исследовали механические свойства сферических и купольных конструкций. Оказалось, что они не только обладают отличной аэродинамикой, но и намного прочнее прямоугольных.

Энергетически сферическая поверхность безупречна. При максимальном внутреннем объеме она имеет минимальную площадь. Поэтому в купольном строении потери тепла во внешнюю среду в несколько раз меньше, чем в обычном доме. Не зря обитатели арктики эскимосы веками строили сферические домики «иглу» из снега. Практический опыт подсказал им, какой должна быть ветростойкая и энергоэффективная конструкция.

В наши дни сферические дома из области теоретики перешли в разряд практических технологий экологического строительства. Тысячи людей во всем мире успели оценить их преимущества и не жалеют о своем выборе.

Примеры и разновидности купольных конструкций

Сферическую конструкцию можно построить двумя способами:

• В виде геодезического купола (собирается из треугольных каркасных ячеек, стыкуемых с помощью узловых элементов — коннекторов).
• Из гнутых стоек или сегментов арочной формы, соединяемых вершинами (стратодезический купол).

Гнутоклееные деревянные стойки для сборки стратодезического купола
По технологии стратодезического купола собирают «маковки» православных храмов. Геодезический купол пришел к нам из Америки. Его изобретателем считают инженера Фуллера.

Несмотря на различия во внешнем виде, эти конструкции отличаются минимальным весом, высокой жесткостью и устойчивостью.

Дома в форме сферы можно строить из любого материала, начиная от пенопласта и заканчивая бетоном. Выбор конкретного варианта зависит от технической оснащенности исполнителя. Для возведения жилых зданий чаще всего используют конструкции с деревянным каркасом.

Причин для этого несколько. Древесина – экологичный и прочный материал, обладающий высокой упругостью. Геодезические купола собирают из деревянных балок, соединяя их стальными коннекторами.

Каркас дома на основе геодезического купола

Стратодезические жилые конструкции строят из гнутоклееных балок.

Каркас здания на основе стратодезического купола

Японская технология сферических зданий основана на использовании гнутых пенопластовых блоков с замками. Из них собирают небольшие одноэтажные постройки. Пенопласт в таком доме выполняет сразу две функции: конструкционного материала и утеплителя.

Современный домик-«иглу» строится не из снега, а из пенопластовой «скорлупы»

Минимальный вес дома-сферы позволяет возводить его на мелкозаглубленном ленточном или свайном фундаменте. Для утепления секций используют минвату, солому, эковату или пенопласт.

Наиболее распространенный вид кровельного покрытия – мягкая битумная черепица. Этот материал идеально ложится на криволинейные поверхности.

Дом-сфера, покрытый битумной черепицей

Сторонники экостроительства делают выбор в пользу деревянного гонта – тонких дощечек, образующих оригинальное чешуйчатое покрытие.

Деревянный гонт естественно смотрится на сферическом здании Двухуровневый дом на основе стратодезического купола с гонтовой облицовкой

Недавно на рынке появились новые материалы, идеально адаптированные для создания бесшовного кровельного ковра. Это «жидкая пробка» (частицы пробкового дерева в акриловом полимере) и жидкая резина.

Как мы уже говорили, материал для строительства сферического дома может быть разнообразным. Если вам больше нравится бетон, нет проблем.

Используя технологию набрызга, можно возводить купольные постройки из легкого бетона

Современные технологии позволяют строить такие дома с помощью пневмоопалубки из ПВХ, на которую наносится вспененный утеплитель. Затем по утеплителю ставят арматурный каркас и наносят на него бетонную смесь методом торкретирования.

Из одних соломенных блоков дом-сферу не построишь. Этот материал используют как утеплитель. Солому плотно набивают в ячейки из досок и собирают из них купол.

Пространственный каркас выполнен из деревянных ячеек, наполненных соломой

Особенности строительства

Еще совсем недавно дом-купол был строительной экзотикой. За его возведение брались энтузиасты экологического движения и любители оригинальных конструкций. Сегодня интернет наполнен заводскими комплектами сферических домов. Необычное жилище на основе геодезического купола и стратодезическую конструкцию можно купить, не выходя из городской квартиры.

Тем же, кто предпочитает все делать собственными руками, мы рекомендуем остановиться на геодезическом куполе. В сборке он немного сложнее дома-сферы из полуарок, но зато не требует сложного оборудования для гнутья и склеивания древесины.

Самый ответственный узел конструкции – коннектор. От точности его изготовления зависит пространственная стыковка всех элементов. Поэтому для работы лучше купить готовый заводской комплект.

Следующий шаг – подготовка ребер каркаса из деревянных брусков толщиной 50 мм. Их ширина должна быть равной толщине утеплителя (минимум 10 см). Длину ребер выбирают, ориентируясь на сборочную схему геокупола.

Необходимое пояснение: в расчетах купольных каркасов используется термин «частота» или «сечение», обозначаемые символом V. Им определяется плотность разбивки поверхности купола на треугольники. Чем больше частота, тем менее «угловатой» и более шарообразной получается купольная конструкция.

Однако, увеличение частоты вызывает рост количества ребер и коннекторов, существенно усложняя конструкцию. Поэтому на практике чаще всего строят купольные дома с частотой 2V.

Частота разбивки (V) поверхности купола – базовый элемент расчетов

Кроме частоты нужно определиться с диаметром купола и его высотой. Если вы купите готовый комплект коннекторов, то пользоваться онлайн калькулятором для расчета длин ребер вам не придется. Изготовитель делает коннекторы для сборки каркаса заданной высоты и диаметра.

Как показывает практика, купол диаметром 8 метров и высотой 4 метра оптимален для сооружения двухуровневого дачного дома общей площадью 64 м2, зимнего сада или сауны.

Для того, чтобы построить купольный дом своими руками нужно выполнить несколько операций:

• Разметить на участке фундамент под каркас (ленточный, столбчатый, «шведская плита» или свайный).
• На стадии бетонирования заложить в фундамент анкера. Они нужны для крепления подкладочного бруса, к которому фиксируют первый ряд «треугольников» каркаса.
• Сборку ведут параллельными рядами, связывая ребра каркаса в пространственную конструкцию с помощью коннекторов.
• Завершив монтаж, купол изнутри обшивают деревянной вагонкой или гипсокартонном.
• В ячейки каркаса закладывают утеплитель, накрывают его ветрозащитной мембраной и обшивают снаружи плитой Изоплат или OSB.
• В местах установки окон обшивку не делают. В зоне установки дверей каркас «разрывают», оставляя в нем нишу нужного размера. Жесткость геодезического купола очень высокая, поэтому дверные проемы не могут ее существенно уменьшить.

Двухуровневый дом-сфера на стадии наружной обшивки плитой OSB
Некоторые застройщики делают первый этаж в виде многогранника, а второй венчают геокуполом.

Дверной проем идеально вписывается в дизайн сферического здания. А вот треугольные окна и доборные элементы дверной коробки обходятся дороже обычных. Их приходится заказывать как нестандартные изделия.

Достоинства и интерьер купольных домов

Кроме упомянутых преимуществ – уникальной прочности и ветростойкости, сферические строения обладают и другими достоинствами:

• экономичностью (за счет легкого фундамента, сборки без привлечения кранов, использования эффективного утеплителя);
• возможностью свободной планировки жилого пространства благодаря отсутствию внутренних стен;
• отличными звукоизоляционными качествами;
• привлекательным внешним видом и уникальным интерьером.

Внутри круглые здания на удивление вместительны и красивы. Большая высота позволяет без проблем размещать в них второй этаж.

Даже под небольшим 4-х метровым куполом можно разместить комфортную баню. Сферическая форма и центральное расположение печи обеспечивают экономию тепла и равномерный прогрев помещений.

Сауна под куполом – компактно и удобно

Характер отзывов о купольных домах в большинстве своем положителен. Владельцам нравится оригинальная форма, комфорт и вместительность этих построек.

Экономия энергоносителей, низкие затраты на строительство сферических зданий также часто упоминаются в комментариях их хозяев.

Из субъективных положительных эмоций следует отметить покой и умиротворенность, ощущаемые человеком в таком доме.

Источник

Ответ:

3)  Радиус сферы купола равен 67,5 см.

4) Площадь купола зонта приближенно равна 11445 см².

Объяснение:

3) Дополним рисунок 2 точками А, В и Н на рисунке.

По условию сказано, что ОС =R ,  СН = h = 27 см .  Тогда

HO = OC – CH;

HO= R- 27 .

Обозначенный на рисунке  отрезок АВ = d = 108 см.  Точка Н – середина АВ. Значит, АН =ВН= 108 : 2 =54 см.

Рассмотрим Δ ОНВ – прямоугольный , в котором HO= R- 27,  ОВ =R, ВН = 54 см.

Применим теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Раскроем скобки, применяя формулу сокращенного умножения

и решим уравнение

Значит, радиус сферы купола равен 67,5 см.

4) Марьяна нашла площадь купола, как площадь сферического сегмента по формуле

где

R- радиус сферы

h- высота высота сегмента

По условию h=27 см , а радиус сферы найден в задаче 3 и равен 67,5 см. Число по условию округлить до 3,14 .

Подставим все значения и найдем площадь.

см².

         

По условию полученное число надо округлить до целого

Если число округляют до какого – нибудь разряда, то все стоящие за этим разрядом цифры заменяют нулями, а если они стоят после запятой, то их отбрасывают.

Если первая отброшенная или  замененная цифра равна

5, 6, 7, 8 или 9 , то стоящую перед ней цифру увеличивают на единицу.

Если первая отброшенная или  замененная цифра равна 0, 1, 2, 3 или 4, то стоящую перед ней цифру оставляют без изменения.

см ².

Тогда площадь купола зонта приближенно равна 11445 см².