- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Площадь
- Площадь квадрата
Площадь квадрата равна квадрату его стороны.
Доказательство
Дано: квадрат,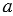 
– сторона квадрата, 
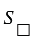– площадь квадрата.
Доказать: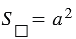 
.
Доказательство:
1 случай
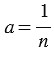, где 
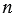– целое число. Возьмем квадрат со стороной 1, разобьем его на 
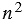равных квадратов (на рисунке 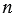= 5).
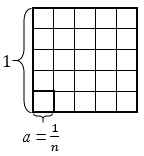
Площадь большого квадрата равна 1, следовательно, чтобы найти площадь каждого маленького квадратика, нужно площадь большого квадрата разделить на количество маленьких квадратиков, число которых 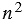, т.е. получим 
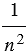– площадь каждого маленького квадратика. Сторона каждого маленького квадрата равна 
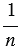, значит, равна 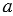, т.к. 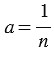. Получаем
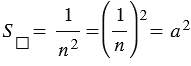. (1)
2 случай
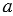– конечная десятичная дробь, содержащая 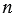знаков после запятой (если 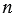= 0, то 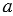– целое число),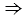 
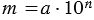– целое число. Разобьем данный квадрат со стороной 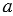на 
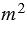равных квадратов (на рисунке 
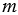= 7).
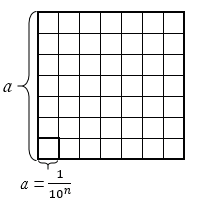
Каждая сторона данного квадрата разобьется на 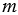равных частей, тогда сторона любого маленького квадрата равна 
.
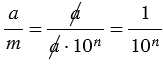По формуле (1) площадь маленького квадрата равна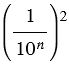 
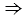, чтобы найти площадь данного квадрата, нужно умножить число маленьких квадратов на их площадь, т.е. 
.
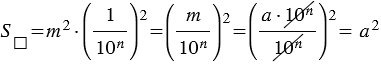3 случай
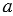– бесконечная десятичная дробь. Рассмотрим число 
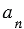, получаемое из 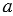отбрасыванием всех десятичных знаков после запятой, начиная с 
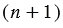– го. Так как число 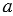отличается от числа 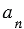не более чем на 
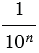, то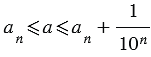 
, откуда
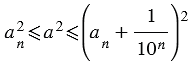. (2)
Площадь 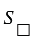данного квадрата заключена между площадью квадрата со стороной 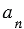и площадью квадрата со стороной 
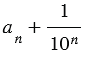(смотри рисунок ниже),
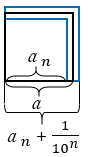
т.е. между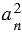 
и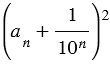 
, значит:
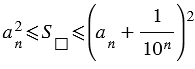. (3)
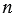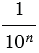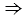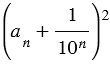Если неограниченно увеличивать число , то число будет становиться сколь угодно малым, число будет сколь угодно мало отличаться от числа 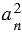. Поэтому из неравенств (2) и (3) следует, что число 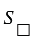сколь угодно мало отличается от числа 
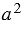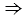
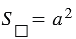, . Что и требовалось доказать.
Советуем посмотреть:
Понятие площади многоугольника
Площадь прямоугольника
Площадь параллелограмма
Площадь треугольника
Площадь трапеции
Теорема Пифагора
Теорема, обратная теореме Пифагора
Формула Герона
Площадь
Правило встречается в следующих упражнениях:
7 класс
Задание 449,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 450,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 457,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 458,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 506,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 876,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1123,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1128,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1136,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1211,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
{S = a ^2}
На этой странице вы найдете удобный калькулятор для расчета площади квадрата и формулы, которые помогут найти площадь квадрата через его сторону, диагональ, периметр, а также радиусы вписанной и описанной окружности.
Квадрат – четырёхугольник, у которого все углы прямые (90 градусов) и все стороны равны между собой. Из-за своих свойств квадрат часто называют правильным четырехугольником.
Содержание:
- калькулятор площади квадрата
- формула площади квадрата через сторону
- формула площади квадрата через диагональ
- формула площади квадрата через радиус вписанной окружности
- формула площади квадрата через радиус описанной окружности
- формула площади квадрата через периметр
- примеры задач
Формула площади квадрата через сторону
S = a ^2
a – сторона квадрата
Формула площади квадрата через диагональ
S=dfrac{d^2}{2}
d – диагональ квадрата
Формула площади квадрата через радиус вписанной окружности
S = 4r^2
r – радиус вписанной окружности
Формула площади квадрата через радиус описанной окружности
S = 2R^2
R – радиус описанной окружности
Формула площади квадрата через периметр
S = dfrac{P^2}{16}
P – периметр квадрата
Примеры задач на нахождение площади квадрата
Задача 1
Найдите площадь квадрата если его диагональ равна 1.
Решение
Для решения задачи воспользуемся формулой.
S = dfrac{d^2}{2} = dfrac{1^2}{2} = dfrac{1}{2} = 0.5 : см^2
Ответ: 0.5 см²
Проверим ответ на калькуляторе .
Задача 2
Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Решение
Для решения этой задачи используем формулу площади квадрата через радиус описанной окружности.
S = 2R^2 = 2 cdot 83^2 = 2 cdot 6889 = 13778 : см^2
Ответ: 13778 см²
Проверим ответ с помощью калькулятора .
Задача 3
Найдите площадь квадрата если его сторона равна 8 см.
Решение
Используем первую формулу.
S = a ^2 = 8 ^2 = 64 : см^2
Ответ: 64 см²
Проверим результат на калькуляторе .
Задача 4
Найдите площадь квадрата периметр которого равен 456 см.
Решение
Используем формулу для площади квадрата через периметр.
S = dfrac{P^2}{16} = dfrac{456^2}{16} = dfrac{456 cdot cancel{456}^{ : 57}}{cancel{16}^{ : 2}} = dfrac{57 cdot cancel{456}^{ : 228}}{cancel{2}^{ : 1}} = 57 cdot 228 = 12996 : см^2
Ответ: 12996 см²
Проверка .
Задача 5
Найдите площадь квадрата со стороной 15 см.
Решение
Воспользуемся формулой площади квадрата через сторону.
S = a ^2 = 15 ^2 = 225 : см^2
Ответ: 225 см²
Проверка .
По какой формуле рассчитывается площадь квадрата?
Анонимный вопрос
2 ноября 2018 · 54,7 K
6,8 K
Комментировать ответ…Комментировать…
Увлекаюсь бухгалтерией, математикой, педагогикой, статистикой. Люблю точные науки. · 8 нояб 2018
Существует 5 формул для нахождения площади квадрата:
1. S=a⋅a=a2 – формула площади квадрата через сторону,
2. S = ½ d² – формула площади квадрата через диагональ,
3. S=4⋅r² – формула площади квадрата через радиус вписанной окружности,
4. S=2⋅R² – формула площади квадрата через радиус описанной окружности,
5. S= Р²/ 16 – формула площади квадрата через периметр… Читать далее
33,8 K
Комментировать ответ…Комментировать…
Engineer – programmer ⚡⚡ Разбираюсь в компьютерах, технике, электронике, интернете и… · 2 нояб 2018 ·
Посчитать площадь квадрата можно через его диагональ по формуле: S = ½ d²,
где d — диагональ, т.е. отрезок, который соединяет два противоположных не смежных угла квадрата. Диагональ разделяет квадрат на два равных прямоугольных треугольника.
10,7 K
Комментировать ответ…Комментировать…
Хорошист преуспеваю в Биологии , Географии и Геометрии · 4 мая 2022
Привет, сейчас расскажу максимально доходчиво ,чтобы найти его площадь нам надо знать одну сторону, если одна сторона ровна 6 то тебе надо возвести число в квадрат, и получится 36 то есть тебе надо сторону возвести в квадрат все очень просто надеюсь ,что помог
637
Комментировать ответ…Комментировать…
Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.
Площади равных фигур равны. Их периметры тоже равны.
Площадь квадрата
Запомните!
Для вычисления площади квадрата нужно умножить его длину на саму себя.
S = a · a
Пример:
SEKFM = EK · EK
SEKFM = 3 · 3 = 9 см2
Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:
S = a2
Площадь прямоугольника
Запомните!
Для вычисления площади прямоугольника нужно умножить его длину на ширину.
S = a · b
Пример:
SABCD = AB · BC
SABCD = 3 · 7 = 21 см2
Запомните!
Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.
Площадь сложных фигур
Запомните!
Площадь всей фигуры равна сумме площадей её частей.
Задача: найти площадь огородного участка.
Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.
Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.
SABCE = AB · BC
SEFKL = 10 · 3 = 30 м2
SCDEF = FC · CD
SCDEF = 7 · 5 = 35 м2
Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = SABCE + SEFKL
S = 30 + 35 = 65 м2
Ответ: S = 65 м2 — площадь огородного участка.
Свойство ниже может вам пригодиться при решении задач на площадь.
Запомните!
Диагональ прямоугольника делит прямоугольник на два равных треугольника.
Площадь любого из этих треугольников равна половине площади прямоугольника.
Рассмотрим прямоугольник:
АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников
ABC и
ACD
Вначале найдём площадь прямоугольника по формуле.
SABCD = AB · BC
SABCD = 5 · 4 = 20 см2
S
ABC = SABCD : 2
S
ABC = 20 : 2 = 10 см2
S
ABC =
S
ACD = 10 см2
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».
Оставить комментарий:
3 декабря 2015 в 22:54
Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
как написать правильно площадь треугольника?
0
Спасибо
Ответить
9 декабря 2015 в 19:41
Ответ для Ирина Петренко
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
S(рисуешь мини треугольник) = ,,,,,
0
Спасибо
Ответить
