
{S = a ^2}
На этой странице вы найдете удобный калькулятор для расчета площади квадрата и формулы, которые помогут найти площадь квадрата через его сторону, диагональ, периметр, а также радиусы вписанной и описанной окружности.
Квадрат – четырёхугольник, у которого все углы прямые (90 градусов) и все стороны равны между собой. Из-за своих свойств квадрат часто называют правильным четырехугольником.
Содержание:
- калькулятор площади квадрата
- формула площади квадрата через сторону
- формула площади квадрата через диагональ
- формула площади квадрата через радиус вписанной окружности
- формула площади квадрата через радиус описанной окружности
- формула площади квадрата через периметр
- примеры задач
Формула площади квадрата через сторону

S = a ^2
a – сторона квадрата
Формула площади квадрата через диагональ

S=dfrac{d^2}{2}
d – диагональ квадрата
Формула площади квадрата через радиус вписанной окружности

S = 4r^2
r – радиус вписанной окружности
Формула площади квадрата через радиус описанной окружности

S = 2R^2
R – радиус описанной окружности
Формула площади квадрата через периметр

S = dfrac{P^2}{16}
P – периметр квадрата
Примеры задач на нахождение площади квадрата
Задача 1
Найдите площадь квадрата если его диагональ равна 1.
Решение
Для решения задачи воспользуемся формулой.
S = dfrac{d^2}{2} = dfrac{1^2}{2} = dfrac{1}{2} = 0.5 : см^2
Ответ: 0.5 см²
Проверим ответ на калькуляторе .
Задача 2
Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Решение
Для решения этой задачи используем формулу площади квадрата через радиус описанной окружности.
S = 2R^2 = 2 cdot 83^2 = 2 cdot 6889 = 13778 : см^2
Ответ: 13778 см²
Проверим ответ с помощью калькулятора .
Задача 3
Найдите площадь квадрата если его сторона равна 8 см.
Решение
Используем первую формулу.
S = a ^2 = 8 ^2 = 64 : см^2
Ответ: 64 см²
Проверим результат на калькуляторе .
Задача 4
Найдите площадь квадрата периметр которого равен 456 см.
Решение
Используем формулу для площади квадрата через периметр.
S = dfrac{P^2}{16} = dfrac{456^2}{16} = dfrac{456 cdot cancel{456}^{ : 57}}{cancel{16}^{ : 2}} = dfrac{57 cdot cancel{456}^{ : 228}}{cancel{2}^{ : 1}} = 57 cdot 228 = 12996 : см^2
Ответ: 12996 см²
Проверка .
Задача 5
Найдите площадь квадрата со стороной 15 см.
Решение
Воспользуемся формулой площади квадрата через сторону.
S = a ^2 = 15 ^2 = 225 : см^2
Ответ: 225 см²
Проверка .
Как определить площадь квадрата

О чем эта статья:
3 класс, 8 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Формула нахождения площади квадрата
Квадрат — это фигура, которая является частным случаем прямоугольника, из-за чего можно заметить схожесть некоторых алгоритмов. Способ вычисления всегда зависит от исходных данных. Чтобы узнать площадь квадрата, необходимо знать специальные формулы, рассмотрим пять из них.
Если известна длина стороны
Умножаем ее на то же число или возводим в квадрат.
S = a × a = a 2 , где S — площадь, a — сторона.
Эту формулу проходят в 3 классе. Остальные формулы третьеклассникам знать пока не нужно, но они пригодятся ученикам 8 класса.
Если нам дана диагональ
Возводим ее в квадрат и делим на два.
S = d 2 : 2, где d — диагональ.
Если известен радиус вписанной окружности
Умножаем его квадрат на четыре.
S = 4 × r 2 , где r — это радиус вписанной окружности.
Если у нас есть радиус описанной окружности
Возведем его в квадрат и умножим на два.
S = 2 × R 2 , где R — это радиус описанной окружности.
У нас есть курсы обучения математике для учеников с 1 по 11 классы — записывайтесь!
Если есть периметр
Мы должны возвести его в квадрат и разделить на 16.
S = Р 2 : 16, где Р — это периметр.
Периметр любого четырехугольника равен сумме длин всех его сторон.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
S квадрата. Решение задач
Мы разобрали пять формул для вычисления площади квадрата. А теперь давайте потренируемся!
Задание 1. Как найти площадь квадрата, диагональ которого равна 90 мм.
Воспользуемся формулой: S = d 2 : 2.
Подставим в формулу значение диагонали: S = 90 2 : 2 = 4050 мм 2 .
Ответ: 4050 мм 2 .
Задание 2. Окружность вписана в квадрат. Найдите площадь квадрата, если радиус окружности равен 24 см.
Если окружность вписана в квадрат, то сторона квадрата равна диаметру:
a = d
Диаметр окружности равен двум радиусам:
d = 2r
Получается, что сторона равна двум радиусам:
a = 2r
Используем формулу нахождения площади квадрата через сторону:
S = a 2
Так как из пункта 3 мы получили, что сторона равна двум радиусам, то формула площади квадрата примет вид:
S = (2r) 2
S = 4r 2
Теперь подставим значение радиуса в формулу площади:
S = 4 × 24 2 = 2304 см 2
Онлайн калькулятор площади вписанного в круг квадрата. Как узнать площадь вписанного в круг квадрата.






Вычислить площадь вписанного квадрата через:
Радиус круга R:
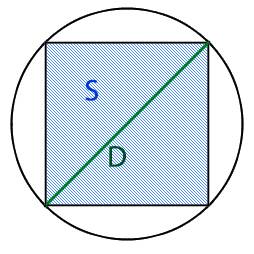
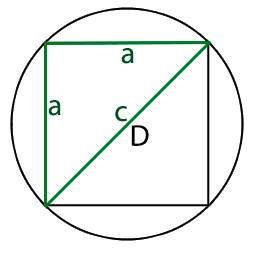
Для того что бы найти площадь вписанного в круг квадрата, нам необходимо узнать длину ребра этого квадрата. Для этого нам необходимо разделить квадрат по диагонали на два равнобедренных треугольника, при этом основание у этих треугольников будет равно диаметру круга.
Следующим действиям мы должны определиться с известной нам величиной круга в которую вписан квадрат, а именно нам должна быть известна:
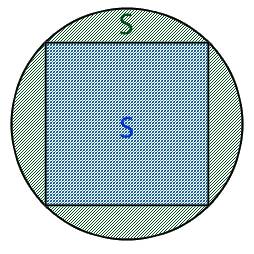
- либо площадь круга, обозначаемая буквой S,
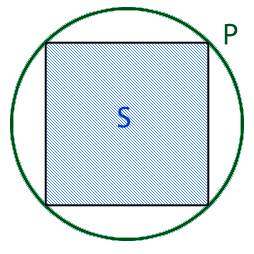
- либо периметр круга, обозначаемый буквой P,
- либо радиус круга, обозначаемый буквой R,
- либо диаметр круга, обозначаемый буквой D.
Начнем по порядку, мы имеем равнобедренный прямоугольный треугольник и для того, что бы узнать длину его ребер нам необходимо воспользоваться теоремой Пифагора исходя из которой
Теперь для того что бы найти длину ребра треугольника (которое равно стороне нашего квадрата) нам необходимо узнать длину основания треугольника, которое равно диаметру круга
1. Если нам известна площадь круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
2. Если нам известна длина круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
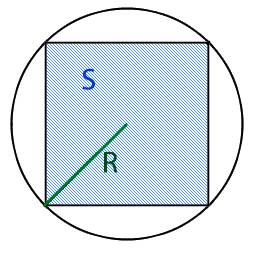
3. Если нам известен радиус круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
Соответственно если мы знаем диаметр круга который равен основанию треугольника полученного путем разделения квадрата на две части по диагонали,
мы можем узнать длину сторон квадрата используя теорему Пифагора
после того как мы получили значение длины стороны вписанного квадрата равную a, для получения его площади нам необходимо полученное значение возвести в квадрат.
Как найти площадь квадрата
Как найти площадь квадрата?
Площадь квадрата может быть найдена по его стороне, диагонали, радиусам вписанной и описанной окружности.
1. Площадь квадрата равна квадрату его стороны.
Формула для нахождения площади квадрата по его стороне:
Например, площадь квадрата ABCD можно найти как квадрат его стороны AB:
2. Площадь квадрата равна половине квадрата диагонали его стороны.
Формула для нахождения площади квадрата по его диагонали:
Например, площадь квадрата ABCD можно найти через его диагональ AC:
3. Площадь квадрата в четыре раза больше квадрата радиуса вписанной к него окружности.
Так как
то из формулы площади квадрата по стороне получаем
формулу для нахождения площади квадрата через радиус вписанной окружности:
4. Площадь квадрата равна удвоенному квадрату радиуса описанной около него окружности.
Так как
то из формулы площади квадрата по стороне вытекает
формула для нахождения площади квадрата через радиус вписанной окружности:
[spoiler title=”источники:”]
http://tamali.net/calculator/inscribed/square/area/
[/spoiler]
Что такое квадрат и понятие его площади
Квадрат — простейшая плоская геометрическая фигура. Является одновременно правильным четырёхугольником и прямоугольником, все стороны которого равны.
Состоит соответственно из четырёх равных сторон, четырёх вершин ABCD и прямых углов 90°.
Под площадью квадрата подразумевается пространство, ограниченное его сторонами (та часть плоскости, что внутри). Способов расчёта существует немного, а формулы для вычисления площади весьма простые.
Как найти площадь квадрата через сторону
Данный способ и калькулятор позволит найти площадь квадрата через значение длины его сторон — введите его в соответствующее поле. В зелёном поле автоматически выведется результат.
Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …
Как найти площадь квадрата через периметр
Данный способ и калькулятор позволит найти площадь квадрата через значение его периметра — введите его в соответствующее поле. В зелёном поле выведется результат.
Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …
Как найти площадь квадрата через диагональ
Данный способ и калькулятор позволит найти площадь квадрата через значение длины его диагонали — введите его в соответствующее поле. В зелёном поле получите результат.
Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …
Как найти площадь квадрата через радиус вписанной окружности
Данный способ и калькулятор позволит найти площадь квадрата через значение радиуса вписанной окружности — введите его в соответствующее поле. В зелёном поле выведется результат.
Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …
Как найти площадь квадрата через радиус описанной окружности
Данный способ и калькулятор позволит найти площадь квадрата через значение радиуса описанной окружности — введите его в соответствующее поле. В зелёном поле выведется результат автоматически.
Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …
Ваша оценка?
[Оценок: 5 / Средняя: 4.6]
Расчёт площади квадрата по радиусу описанной окружности
Калькулятор рассчитывает площадь квадрата по радиусу описанной окружности.
Формула площади квадрата по радиусу описанной окружности
Где S – площадь квадрата,
R – радиус описанной окружности
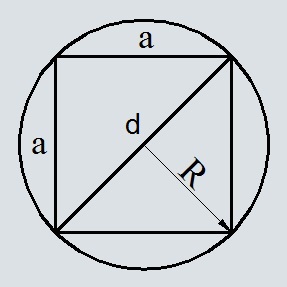
Вывод формулы площади квадрата по радиусу описанной окружности

Диагональ квадрата равна диаметру окружности или двум радиусам
С помощью теоремы Пифагора выведем сторону a через диагональ
Подставим в формулу площади квадрата
Диагональ квадрата равна диаметру окружности или двум радиусам
Подставим и выведем формулу
Похожие калькуляторы
Кроме стандартного произведения сторон в геометрии есть еще как минимум пять методов, о которых я хочу сейчас рассказать. Итак, поехали!
Формула 1. Площади квадрата через его диагональ
Выводится элементарно через один из прямоугольных треугольников.
Формула 2. Через периметр
Получается подстановкой в стандартную формулу площади значения а = p/4.
Формула 3. Через отрезок из вершины квадрата к середине противоположной стороны
Аналогично всё выводится из прямоугольного треугольника ABE.
Формула 4. Через радиус вписанной окружности
Очевидно, что радиус вписанной окружности равен половине стороны квадрата, исходя из чего, и выводится формула.
Формула 5. Через радиус описанной окружности
Вот такая тривиальная геометрия в это солнечное субботнее утро. Спасибо за внимание, уважаемые Читатели!
