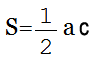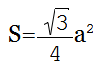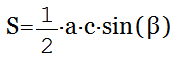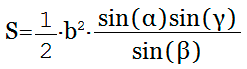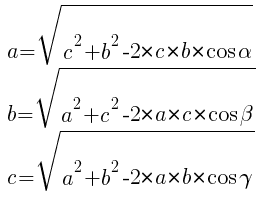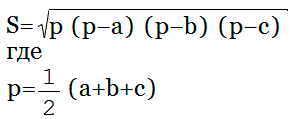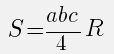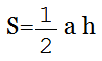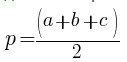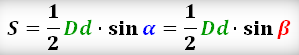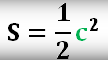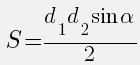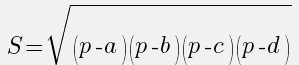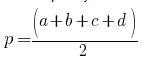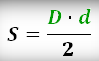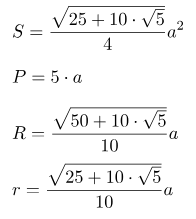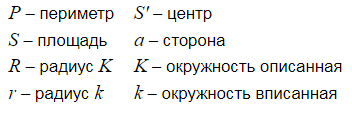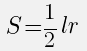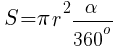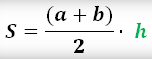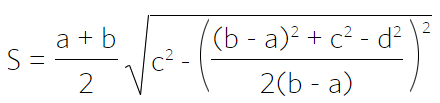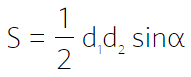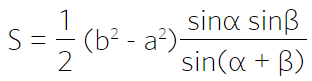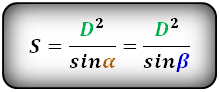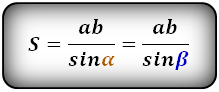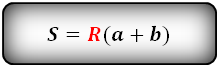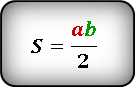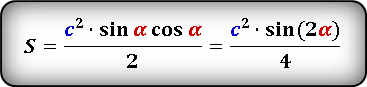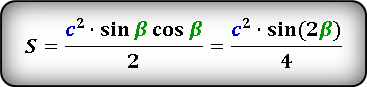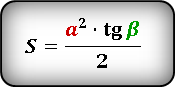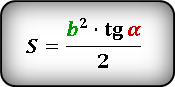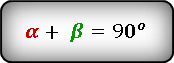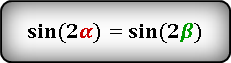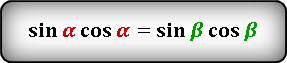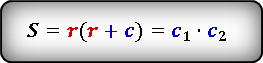Учебник
Геометрия, 9 класс
Формулы площадей через синус угла
Основные свойства площадей фигур:
- Равные фигуры имеют равные площади. Две фигуры состоящие из одинаковых кусков – равновеликие.
- Аддитивность: Площадь фигуры, разрезанной на несколько частей, равна сумме площадей этих частей ;
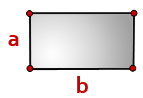
- Площадь прямоугольника равна произведению ширины на длину … произведение сторон.
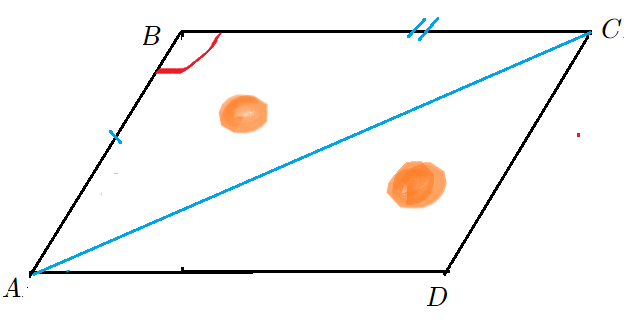
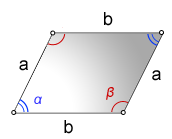
Задача 1: В параллелограмме известны стороны $7$, $10$ и синус угла между ними $frac{1}{2}$. Найти площадь параллелограмма.
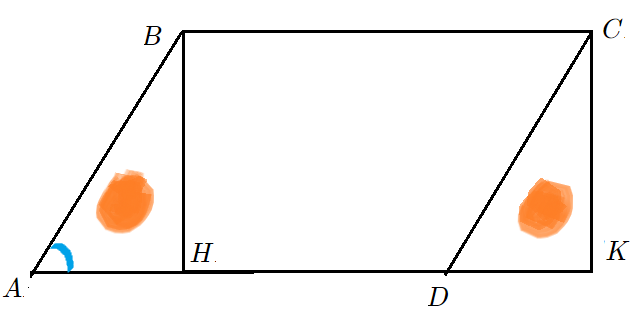
- Решение: Опустим высоты $BH$ и $CK$ на основание $AD$ . Они помогут “увидеть” площадь.
- Что есть синус $angle BAH$ в прямоугольном треугольнике $bigtriangleup ABH$? Отношение катета $BH$ к гипотенузе $AB$.
- Формула синуса позволит выразить высоту $BH$ через сторону $AB$ и синус $frac{1}{2}$. Высота $CK$ такая же.
- Параллелограмм $ABCD$ состоит из кусков: $bigtriangleup ABH$ и $4$-угольник $HBCD$. Площадь – сумма площадей кусков.
- Прямоугольник $HBCK$ состоит из кусков $HBCD$ и $bigtriangleup DCK$. Площадь также “сумма кусков”.
- Треугольники $bigtriangleup ABH$ и $bigtriangleup DCK$ одинаковые. Значит, параллелограмм и прямоугольник равновеликие.
- Площадь Параллелограмма $ABCD$ так же, как прямоугольника $HBCD$ равна высота на основание.
- $S_{ABCD}=S_{ABH}+S_{HBCD}=S_{HBCD}+S_{DCK}=S_{HBCK}=BHcdot HK=ABcdotsin angle BADcdot AD=7cdotfrac{1}{2}cdot10$
Теорема “о площади параллелограмма и треугольника через синус угла”:
- Площадь параллелограмма равна произведению сторон на синус угла параллелограмма:
- Формулы $S=acdot bcdotsin angle BAD$ $S_{ABCD}=ABcdot BCcdotsin D$
- Площадь треугольника равна половине произведения сторон треугольника на синус угла между ними.
- Формулы $S=frac{1}{2}cdot acdot bcdotsin angle C$ $S_{bigtriangleup ABC}=frac{1}{2}cdot ABcdot BCcdotsin angle CBA$
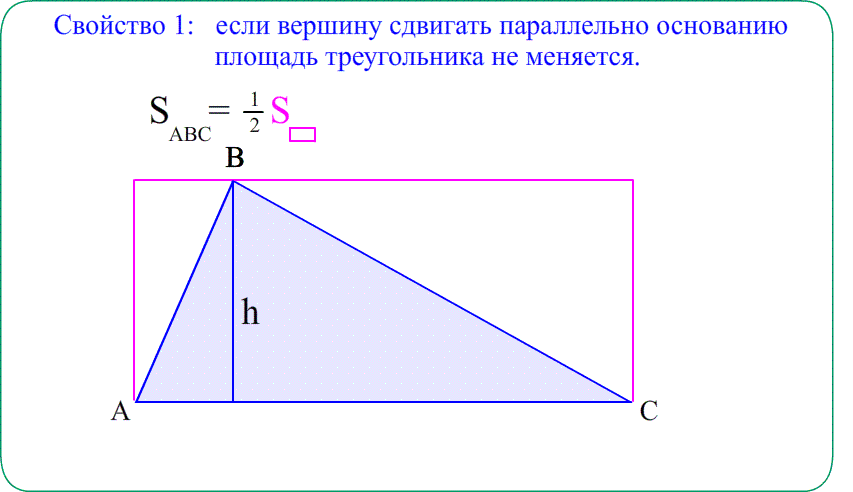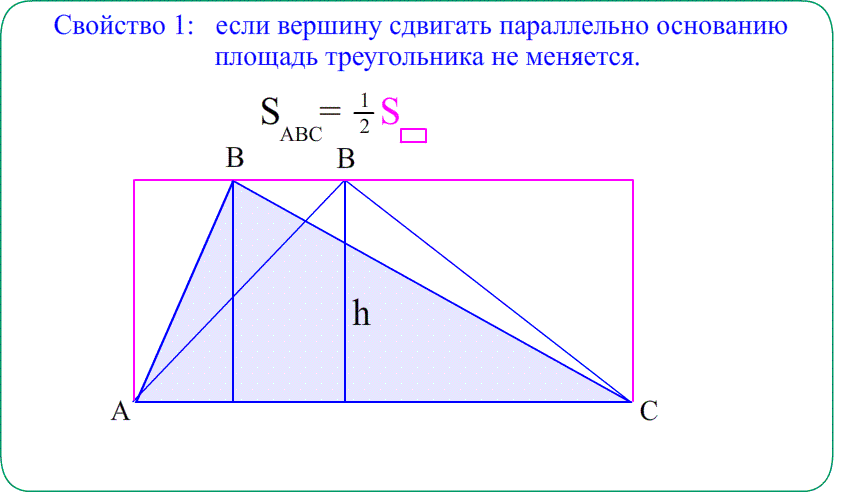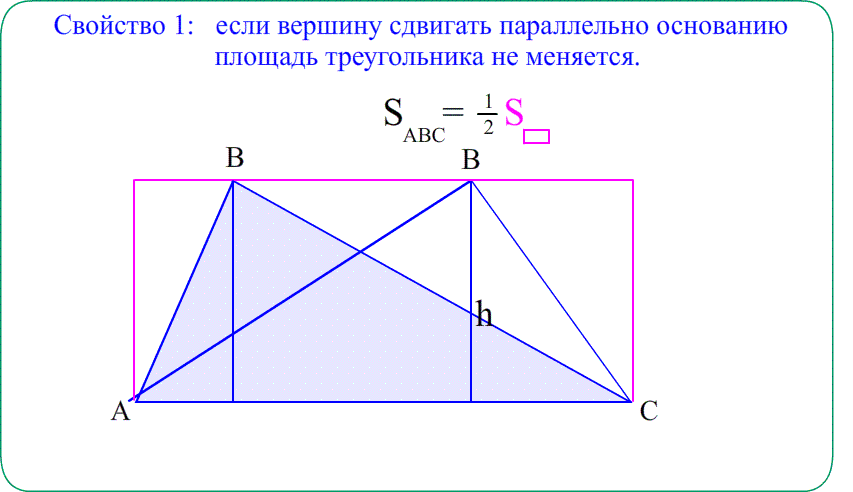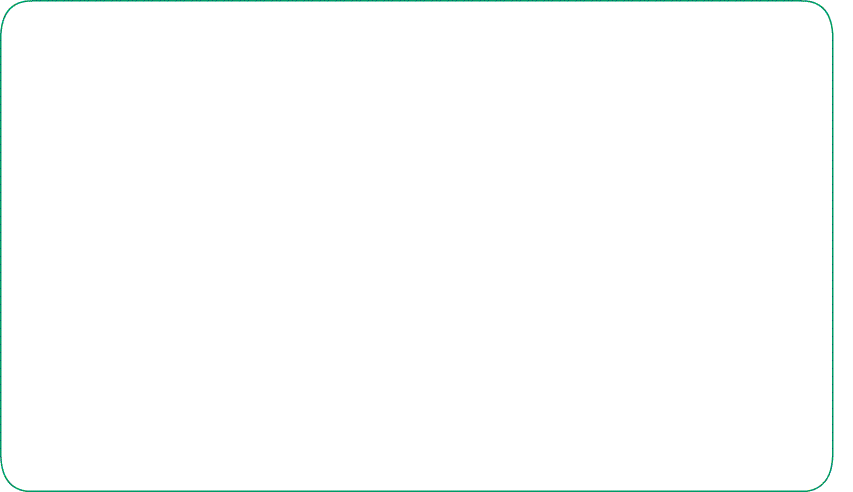
Площадь треугольника также легко получить через площадь параллелограмма, равновеликого с двумя треугольниками, приставленными друг к другу по диагонали. Тогда площадь одного треугольника будет равна половине площади параллелограмма с тем же основанием и с той же высотой.
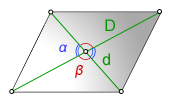
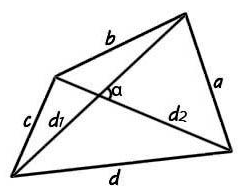
Задача 2: Диагонали четырехугольника делятся точкой пересечения на отрезки $3$, $5$ и $6$, $7$ . Синус угла между диагоналями $0,2$. Найти площади треугольников и всего четырехугольника.
- Дано: $BO=3$ $OD=5$ $CO=6$ $AO=7$ … угол между $sinangle AOB=0,2$. Найти: $S_{ABCD}=?$.
- Решение: Диагонали делят четырехугольник на 4 треугольника. Площадь = сумме 4-х площадей.
- Аддитивность: $S_{ABCD}=S_{bigtriangleup AOB}+S_{bigtriangleup BOC}+S_{bigtriangleup COD}+S_{bigtriangleup AOD}$.
- Площадь одного из них по формуле: $S_{bigtriangleup AOB}=frac{1}{2}cdot AOcdot OBcdot sin angle AOB=frac{1}{2}cdot 7 cdot 3cdot 0,2=2,1$
- Каковы синусы остальных углов? Свойство: Синусы смежных углов равны: $sinangle BOC=sinangle COD=sinangle AOD=0,2$
- Тогда, площади других треугольников $frac{1}{2}cdot 3 cdot 6cdot 0,2=1,8$ $frac{1}{2}cdot 6 cdot 5cdot 0,2=3$ $frac{1}{2}cdot 5 cdot 7cdot 0,2=3,5$
- Площадь четырехугольника равна сумме этих площадей Ответ: $S_{ABCD}=2,1+1,8+3+3,5=10,4$
Теоретически, по-другому: Распишем получение площади $S_{ABCD}$ в буквах, без числовых значений:
- $frac{1}{2}cdot OAcdot OBcdot sin angle AOB+frac{1}{2}cdot OBcdot OCcdot sin angle AOB+frac{1}{2}cdot OCcdot ODcdot sin angle AOB+frac{1}{2}cdot ODcdot OAcdot sin angle AOB$
- Вынос за скобки множителей $S_{ABCD}=frac{1}{2}cdot sin angle AOBcdot left(OAcdot OB+OBcdot OC+OCcdot OD+ODcdot OAright)$
- $S_{ABCD}=frac{1}{2}cdot sin angle AOBcdot left(OBcdotleft(OA+OCright)+ODcdotleft(OA+OCright)right)=frac{1}{2}cdot sin angle AOBcdot AC cdot (OB+OD)$
- Получаем $S_{ABCD}=frac{1}{2}cdot AC cdot BDcdot sin angle AOB$ $Rightarrow$ $S_{ABCD}=frac{1}{2}cdot (7+6) cdot (3+5)cdot 0,2=13cdot 0,8=10,4$

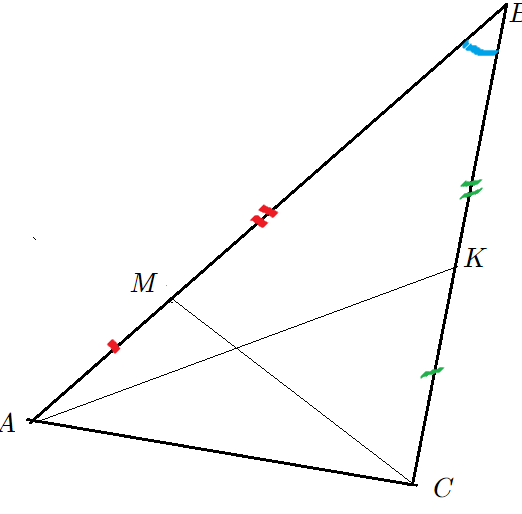
Задача 3: В треугольнике известны стороны $AB=10$ , $BC=12$ и угол $angle ABC=30$ . Точка $M$ делит сторону $AB$ в отношении 3 : 5, а точка $K$ делит сторону $BC$ в отношении 2 : 3. Найти площади и отношение площадей треугольников $ABK$ и $MBC$.
- Дано: $AB=10$, $BC=12$, $frac{AM}{MB}=frac{3}{5}$, $frac{BK}{KC}=frac{2}{3}$, $angle ABC=30$. Найти: $frac{S_{bigtriangleup ABK}}{S_{bigtriangleup MBC}}=?$
- Точка делит отрезок в известном соотношении. Находим части как систему уравнений $frac{x}{y}=?$ $x+y=?$
- $frac{AM}{MB}=frac{3}{5}$, аддитивность $AM+MB=AB=10$ $Rightarrow$ $frac{AM}{AB}=frac{3}{3+5}$ $Rightarrow$ $AM=frac{15}{4}$, $MB=frac{25}{4}$
- $frac{BK}{KC}=frac{2}{3}$, $BK+KC=12$ из свойств пропорций $BK=frac{24}{5}$, $KC=frac{36}{5}$
- Найдем площадь через синус $S_{bigtriangleup ABK}=frac{1}{2}cdot AB cdot BK cdot sin angle ABC = frac{1}{2}cdot 10 cdot frac{24}{5} cdot sin 30= 24 cdot 0,5=12$
- В треугольнике $MBC$ тот же угол, $S_{bigtriangleup MBC}=frac{1}{2}cdot MB cdot BC cdot sin angle ABC = frac{1}{2}cdot frac{25}{4} cdot 12 cdot 0,5=frac{75}{4}$
- отношение площадей треугольников $frac{S_{bigtriangleup ABK}}{S_{bigtriangleup MBC}}=frac{12}{frac{75}{4}}=frac{16}{25}$ Ответ: $frac{16}{25}$
Замечание, продолжение: Можно ли найти отношение площадей при неизвестных значениях сторон и угла?
- Зная лишь как делят точки $M$ и $K$ стороны треугольника, на какие пропорции ?!
- Дано только $frac{AM}{MB}=frac{3}{5}$, $frac{BK}{KC}=frac{2}{3}$. Выразим отрезки через стороны $AB$ и $BC$.
- Выразим площади $S_{bigtriangleup ABK}$ , $S_{bigtriangleup MBC}$ также через стороны $AB$ и $BC$ и угол $angle ABC$.
- Составим отношение площадей, выразим через стороны и угол. Что получится? Что можно сделать, ?
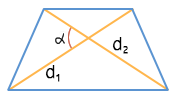
Теорема “о площади четырехугольника через диагонали и синус угла”:
- Площадь четырехугольника равна половине произведения диагоналей на синус угла между ними:
- Формулы $S=frac{1}{2}cdot d_1 cdot d_2 cdotsin angle alpha$ $S_{ABCD}=frac{1}{2}cdot AC cdot BDcdot sin angle AOB$
- Площадь ромба равна половине произведения диагоналей. … диагонали перпендикулярны!
- Формулы $S=frac{1}{2}cdot d_1 cdot d_2=frac{1}{2}cdot AC cdot BD$ $angle AOB=90$ $sin angle AOB=1$
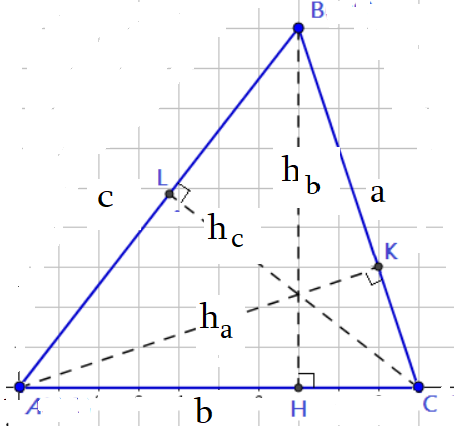
Формулы площади треугольника:
$S=frac{acdot h_a}{2}=frac{acdot bcdotsin C}{2}$ $S=frac{bcdot h_b}{2}=frac{bcdot ccdotsin A}{2}$ $S=frac{ccdot h_c}{2}=frac{ccdot acdotsin B}{2}$.
$sin A=frac{h_b}{c}=frac{h_c}{b}$ $sin B=frac{h_a}{c}=frac{h_c}{a}$ $sin C=frac{h_b}{a}=frac{h_a}{b}$.
$S_{ABC}=frac{1}{2}cdot ACcdot BCcdotsin C$ $S_{ABC}=frac{1}{2}cdot ABcdot BCcdotsin B$ $S_{ABC}=frac{1}{2}cdot ACcdot ABcdotsin A$ .
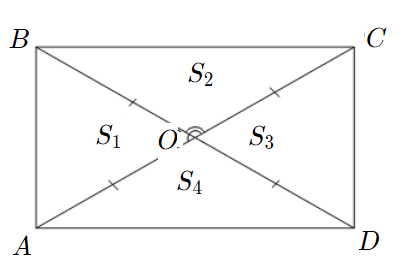
Задача 4: В прямоугольнике диагонали $10$ и угол между ними $30$. Найти площадь.
- Дано: $ABCD$ – прямоугольник , $AC=10$ , $angle AOB=30$ Найти: $S_{ABCD}$ .
- Решение: В прямоугольнике диагонали равны и пересекаются по середине $AO=OB=5$
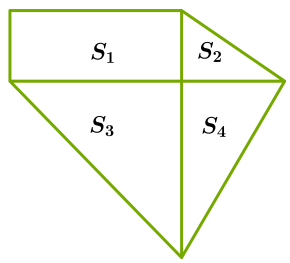
- $bigtriangleup AOB$ и $bigtriangleup COD$ равные $Rightarrow$ $S_1=S_3$ ;
- $bigtriangleup BOC$ и $bigtriangleup AOD$ равные $Rightarrow$ $S_2=S_4$ .
- Смежные, $angle BOC=180-angle AOB=150$. Найдем отношение $frac{S_1}{S_2}=frac{frac{1}{2}AOcdot OBcdotsin30}{frac{1}{2}BOcdot OCcdotsin150}$
- $sin30=sinleft(180-30right)=sin150$. тогда $frac{S_1}{S_2}=frac{frac{1}{2}cdot5cdot5cdotsin150}{frac{1}{2}cdot5cdot5cdotsin150}=1$ Значит, $S_1=S_2$
- Аналогично: $frac{S_3}{S_4}=frac{frac{1}{2}DOcdot OCcdotsin30}{frac{1}{2}AOcdot ODcdotsin150} =1$ $Rightarrow$ $S_3=S_4$, площади равные.
- Диагонали рассекают прямоугольник на четыре равновеликих: треугольника $S_1=S_2=S_3=S_4$ .
- … тогда, по свойству аддитивности площадей $S_1=S_2=S_3=S_4=frac{1}{4}S_{ABCD}$ .
- $S_{AOB}=S_1=frac{1}{2}AOcdot OBcdot sin 30=frac{1}{2}cdot 5cdot 5cdot frac{1}{2}=frac{25}{4}$ $Rightarrow$ $S_{ABCD}=4cdotfrac{25}{4}$
- Найдя площадь АОВ, нашли площадь прямоугольника умножением на 4. Ответ: $S_{ABCD}=25$
Задача 5: Найти площадь ромба $ABCD$, если его высота $EB=12$ , а меньшая диагональ $BD=13$.
- Дано: ромб $ABCD$ , $BD=13$, высота $EB=12$ , Найти: $S_{ABCD}$ .
- Решение: прямоугольный $bigtriangleup BED$, подобен тем, на которые ромб делится диагоналями:
- $bigtriangleup BED sim bigtriangleup AOD=bigtriangleup AOB=bigtriangleup COB=bigtriangleup COD$ . Одинаковый “состав” углов. Все прямоугольные,
- Прямоугольный $bigtriangleup BED$, по Пифагору выразим катет $DE=sqrt{BD^2-BE^2}=5$
- Диагонали в ромбе делятся пополам: $BO=OD=frac{BD}{2}=6,5$ $AO=frac{AC}{2}$ $AC=2cdot AO$
- Для нахождения площади ромба нам нужно найти вторую диагональ.
- $bigtriangleup BED sim bigtriangleup AOD$ $Rightarrow$ $frac{AO}{BE}=frac{OD}{ED}$ $Rightarrow$ $AO=frac{ODcdot BE}{ED}=frac{6,5cdot 12}{5}=15,6$ $AC=2cdot AO=31,2$
- Ответ: Площадь ромба через диагонали: $S_{ABCD}=frac{1}{2}cdot ACcdot BD=0,5cdot 31,2cdot13=202,8$

Задача 6. Площадь равнобедренного треугольника равна $100$ , а угол при вершине $30^o$ 1) Найти его боковые стороны . 2) Найти тригонометрию $15^o$
- Решение: 1) Известны площадь и угол, значит используем формулу площади через синус $30^o$ .
- Пусть боковая сторона $a$ , $S=frac{1}{2}acdot acdotsin30$ , тогда $100=frac{1}{2}a^2cdotsin30$ $Leftrightarrow$ $100=frac{1}{2}a^2cdotfrac{1}{2}$ $Rightarrow$
- $a=sqrt{400}=20$ Ответ: $a=20$
- 2) По теореме косинусов найдем основание $c=sqrt{a^2+a^2-2cdot acdot acdotfrac{sqrt{3}}{2}}=asqrt{2-sqrt{3}}$
- Из вершины равнобедренного угла проведем биссектрису к основанию. По свойству равнобедренности
- она будет и высотой $h$ (треугольник поделится на 2 прямоугольных с углами 15 градусов) и медианой,
- а значит основание поделится пополам , как и угол 30 у вершины поделится по 15 градусов.
- По прямоугольнему треугольнику (половинка): $sin15=frac{0,5cdot c}{a}=frac{0,5cdot acdotsqrt{2-sqrt{3}}}{a}=frac{sqrt{2-sqrt{3}}}{2}$
- Площадь через основание $S=frac{1}{2}cdot ccdot h$, найдем высоту $h=frac{2cdot S}{c}=frac{2cdot0,5cdot a^2cdotsin30}{acdotsqrt{2-sqrt{3}}}=frac{a}{2cdotsqrt{2-sqrt{3}}}$
- В прямоугольном треугольнике стороны $h$, $frac{c}{2}$, $a$. Тогда $cos15=frac{h}{a}=frac{frac{a}{2cdotsqrt{2-sqrt{3}}}}{a}=frac{1}{2cdotsqrt{2-sqrt{3}}}$
Интерактивные Упражнения
Формулы площади геометрических фигур
Площадь геометрической фигуры – численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника
-
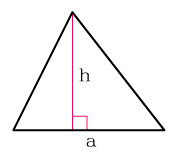
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты -
Формула площади треугольника по трем сторонам
Формула Герона
S = √p(p – a)(p – b)(p – c)
-
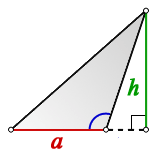
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними. -
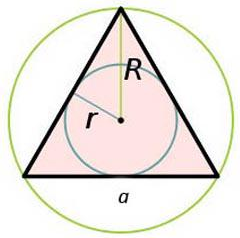
Формула площади треугольника по трем сторонам и радиусу описанной окружности
-
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.где S – площадь треугольника,
a, b, c – длины сторон треугольника,
h – высота треугольника,
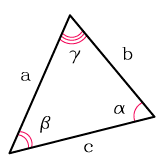
γ – угол между сторонами a и b,
r – радиус вписанной окружности,
R – радиус описанной окружности,p = a + b + c – полупериметр треугольника. 2
Формулы площади квадрата
-
Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.S = a2
-
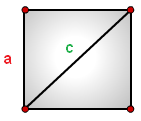
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.где S – площадь квадрата,
a – длина стороны квадрата,
d – длина диагонали квадрата.
Формула площади прямоугольника
Площадь прямоугольника равна произведению длин двух его смежных сторон
S = a · b
где S – Площадь прямоугольника,
a, b – длины сторон прямоугольника.
Формулы площади параллелограмма
-
Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.S = a · h
-
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.S = a · b · sin α
-
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.где S – Площадь параллелограмма,
a, b – длины сторон параллелограмма,
h – длина высоты параллелограмма,
d1, d2 – длины диагоналей параллелограмма,
α – угол между сторонами параллелограмма,
γ – угол между диагоналями параллелограмма.
Формулы площади ромба
-
Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.S = a · h
-
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.S = a2 · sin α
-
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.где S – Площадь ромба,
a – длина стороны ромба,
h – длина высоты ромба,
α – угол между сторонами ромба,
d1, d2 – длины диагоналей.
Формулы площади трапеции
-
Формула Герона для трапеции
S = a + b √(p-a)(p-b)(p-a-c)(p-a-d) |a – b| -
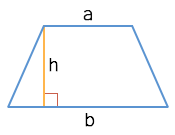
Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы ее оснований на высотугде S – площадь трапеции,
a, b – длины основ трапеции,
c, d – длины боковых сторон трапеции,p = a + b + c + d – полупериметр трапеции. 2
Формулы площади выпуклого четырехугольника
-
Формула площади четырехугольника по длине диагоналей и углу между ними
Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:
где S – площадь четырехугольника,
d1, d2 – длины диагоналей четырехугольника,
α – угол между диагоналями четырехугольника. -
Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)
Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности
S = p · r
-
Формула площади четырехугольника по длине сторон и значению противоположных углов
S = √(p – a)(p – b)(p – c)(p – d) – abcd cos2θ
где S – площадь четырехугольника,
a, b, c, d – длины сторон четырехугольника,
p = a + b + c + d2 – полупериметр четырехугольника,
θ = α + β2 – полусумма двух противоположных углов четырехугольника.
-
Формула площади четырехугольника, вокруг которого можно описать окружность
S = √(p – a)(p – b)(p – c)(p – d)
Формулы площади круга
-
Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.S = π r2
-
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.где S – Площадь круга,
r – длина радиуса круга,
d – длина диаметра круга.
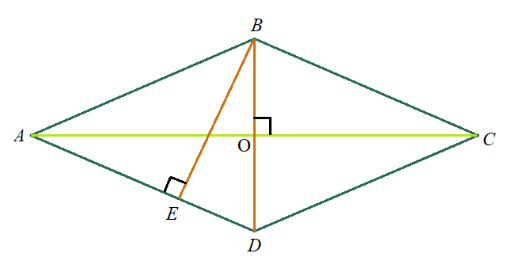
Формулы площади эллипса
Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.
S = π · a · b
где S – Площадь эллипса,
a – длина большей полуоси эллипса,
b – длина меньшей полуоси эллипса.
Содержание:
- Площадь треугольника
- Площадь параллелограмма
- Формула площади прямоугольника
- Площадь квадрата
- Площадь четырехугольника
- Площадь многоугольника
- Площадь ромба
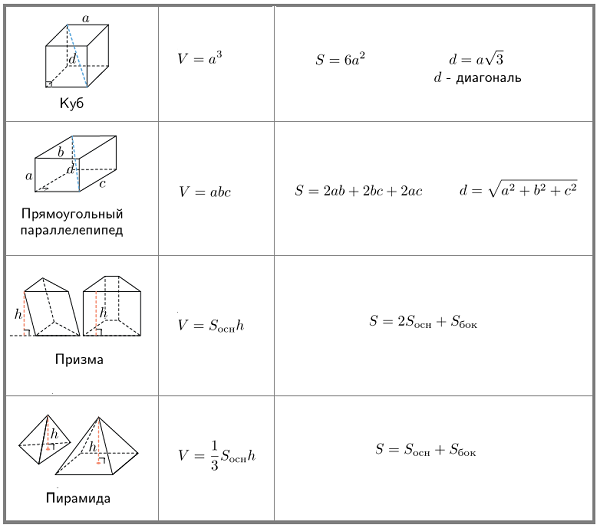
- Площадь многогранника
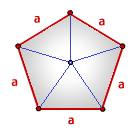
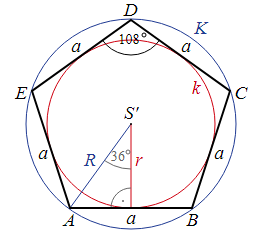
- Площадь пятиугольника
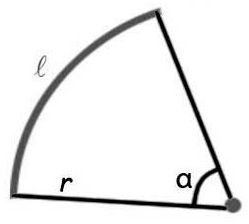
- Площадь закрашенного сектора
- Площадь круга
- Площадь трапеции
Площадь треугольника
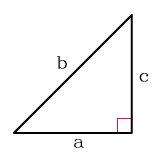
Прямоугольного
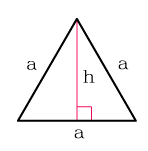
Равностороннего треугольника
Площадь равнобедренного прямоугольного треугольника
S = a2/2
Площадь треугольника через синус
Площадь треугольника через косинус
Для нахождения площади треугольника нужно знать все стороны. По теореме косинусов квадрат неизвестной стороны равен:
Следовательно:
Далее используем формулу Герона:
Площадь треугольника через радиус описанной окружности
Произвольного треугольника
Формула Герона
Площадь треугольника через высоту
Площадь треугольника через полупериметр
Формула Герона
является полупериметром.
Площадь тупоугольного треугольника
S = ah/2
Площадь треугольника через радиус вписанной окружности
S = p×r
где p – полупериметр:
Площадь параллелограмма
Через синус
Через стороны и углы
S = a×b×sin(α) = a×b×sin(β)
Через диагонали и угол между ними
Формула площади прямоугольника
S = a×b
Площадь квадрата
S = a2
Площадь четырехугольника
Выпуклого четырехугольника
где
Площадь многоугольника
S = S1 + S2 + S3 + S4
Правильного многоугольника
где n – количество сторон многоугольника.
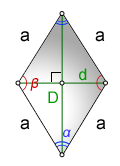
Площадь ромба
Площадь многогранника
Площадь пятиугольника
Площадь закрашенного сектора
Площадь круга
S = πr2
Площадь трапеции
Через основания и высоту
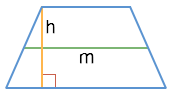
Через высоту и среднюю линию
S = hm
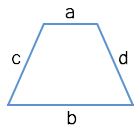
Через четыре стороны
Через диагонали и угол между ними
Через основания и два угла
Все формулы по геометрии. Площади фигур
Чтобы решать задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.
Начнем с квадрата.
Площадь квадрата равна квадрату его стороны.
Площадь прямоугольника равна произведению его длины и ширины.
Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне. Она также равна произведению его сторон на синус угла между ними.
Для площади треугольника есть целых 5 формул. И все они применяются в задачах ЕГЭ.
1) Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне:
2) Она также равна половине произведения его сторон на синус угла между ними:
3) По формуле Герона, где
полупериметр.
4) Также площадь треугольника равна произведению его полупериметра на радис вписанной окружности, S = pr.
5) Еще один способ. Площадь треугольника равна произведению его сторон, деленному на 4 радиуса описанной окружности,
Есть и другие формулы для площади треугольника. Но для решения заданий ЕГЭ, и первой, и второй части, достаточно этих пяти.
Площадь прямоугольного треугольника равна половине произведения его катетов. Она также равна половине произведения гипотенузы на высоту, проведенную к этой гипотенузе:
Площадь правильного треугольника равна квадрату его стороны, умноженному на и деленному на 4:
Площадь трапеции равна произведению полусуммы оснований на высоту,
Также можно сказать, что площадь трапеции равна произведению ее средней линии на высоту,
Площадь произвольного четырехугольника равна половине произведения его диагоналей на синус угла между ними,
Площадь ромба равна произведению квадрата его стороны на синус угла ромба. Она также равна половине произведения диагоналей:
Площадь круга равна произведению числа и квадрата радиуса круга.
Ее также можно записать как произведение числа и квадрата диаметра круга, деленного на 4:
Вспомним важные свойства площадей фигур.
- Равные фигуры имеют равные площади.
Иногда фигуры, имеющие равные площади, еще называют равновеликими. - Если фигура составлена из нескольких фигур, не имеющих общих внутренних точек, то ее площадь равна сумме площадей этих фигур.
Пример. Найдем площадь фигуры, изображенной на клетчатой бумаге с размером клетки 1см1см.
Решение:
Найдем площадь фигуры на рисунке как сумму площадей нескольких фигур.
На рисунке это три треугольника и трапеция, указаны их площади. Тогда площадь фигуры равна 10 + 3,5 + 1,5 + 3 = 18.
Ответ: 18.
3. Отношение площадей подобных фигур равно квадрату коэффициента подобия.
Треугольники АВС и на рисунке называются подобными.
У треугольника все стороны в k раз длиннее, чем у треугольника АВС. Высота треугольника
в k раз длиннее, чем высота треугольника АВС. Тогда площадь треугольника
в
раз больше, чем площадь треугольника АВС.
4. На рисунке показаны треугольники АВС и BCD, имеющие общую высоту. Отношение площадей этих треугольников равно отношению АС к CD:
5. Треугольники АВС и АЕС на рисунке имеют одинаковое основание и разные высоты.
Отношение площадей этих треугольников равно отношению их высот:
6. Медиана треугольника делит его на два равновеликих, то есть равных по площади, треугольника.
На рисунке СМ — медиана треугольника АВС. Площади треугольников АСМ и ВСМ равны.
7. Три медианы треугольника делят его на шесть равных по площади треугольников.
На рисунке все 6 треугольников, из которых состоит треугольник АВС, имеют равные лощади.
Задачи ЕГЭ и ОГЭ по теме: Площади фигур.
Задача 1. Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен
Решение:
Площадь треугольника равна половине произведения его сторон на синус угла между ними. Поэтому
Ответ: 24.
Задача 2. Площадь треугольника ABC равна 4, DE — средняя линия, параллельная стороне AB. Найдите площадь треугольника CDE.
Решение:
Так как DE и АВ параллельны, треугольники CDE и САВ подобны с коэффициентом подобия Площади подобных фигур относятся как квадрат коэффициента подобия. Тогда
Ответ: 1.
Задача 3. У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне?
Решение:
Выразим площадь двумя способами:
Тогда
Ответ: 6.
Задача 4. Площадь треугольника ABC равна 10, DE — средняя линия, параллельная стороне AB. Найдите площадь трапеции ABED.
Решение:
Треугольник CDE подобен треугольнику CAB с коэффициентом Площади подобных фигур относятся как квадрат коэффициента подобия, поэтому
Следовательно, 
Ответ: 7,5.
Задача 5. В параллелограмме ABCD AB = 3, AD = 21, . Найдите большую высоту параллелограмма.
Решение:
Большая высота — это DH, потому что проведена к меньшей стороне. Из треугольника АDН:
Ответ: 18.
Задача 6. Найдите площадь квадрата, если его диагональ равна 1.
Решение:
Квадрат — это частный случай ромба. Площадь квадрата равна половине произведения его диагоналей. Поэтому она равна 0,5.
Ответ: 0,5.
Задача 7. Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1:2.
Решение:
Площадь прямоугольника равна произведению его длины на ширину. Периметр прямоугольника равен сумме длин всех сторон. Пусть одна из сторон прямоугольника равна a, тогда вторая равна 2a. Площадь прямоугольника равна тогда одна из сторон равна 3, а другая 6. Периметр P = 2 · 3 + 2 · 6 = 18.
Ответ: 18.
Задача 8. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.
Решение:
Площадь параллелограмма равна произведению его сторон на синус угла между ними. Площадь прямоугольника равна произведению длины на ширину. Пусть одна сторона параллелограмма и прямоугольника равна вторая равна
а острый угол параллелограмма равен
Тогда площадь параллелограмма равна
а площадь прямоугольника равна
По условию площадь прямоугольника вдвое больше:
Следовательно,
Ответ: 30.
Задача 9. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.
Решение:
Площадь параллелограмма равна произведению его основания на высоту, проведенную к этому основанию. Пусть высоты равны соответственно a и b. Тогда S = 5 · a = 10 · b = 40. Поэтому a = 8, b = 4. Большая высота равна 8.
Ответ: 8.
Задача 10. Найдите площадь ромба, если его высота равна 2, а острый угол 30
Решение:
Площадь ромба равна произведению квадрата его стороны на синус угла ромба. С другой стороны, площадь ромба равна произведению его основания на высоту, проведенную к этому основанию. Пусть сторона ромба равна
Получим уравнение:
Корень уравнения a = 4, поэтому
Ответ: 8.
Задача 11. Найдите площадь ромба, если его диагонали равны 4 и 12.
Решение:
Площадь ромба равна половине произведения его диагоналей.
Ответ: 24.
Задача 12. Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.
Решение:
Трапеция равнобедренная, значит,
Тогда по теореме Пифагора из треугольника ADH:
Ответ: 160.
Задача 13. Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием угол 45
Решение:
Проведем высоту CH. Треугольник CHB — прямоугольный, в нем
значит, он также равнобедренный, CH = HB = 4.
Ответ: 16.
Задача 14. Высота трапеции равна 5, площадь равна 75. Найдите среднюю линию трапеции.
Решение:
Средняя линия трапеции равна полусумме оснований. Выразим её из формулы площади трапеции:
Ответ: 15.
Задача 15. Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ выразите в градусах.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту. Пусть высота равна h, тогда
Из этого уравнения получим: h = 4.
Рассмотрим прямоугольный треугольник, гипотенузой которого является боковая сторона трапеции, равная 8, а катетом — высота трапеции. Длина катета равна половине гипотенузы, следовательно, он лежит напротив угла
Ответ: 30.
Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Задача 16. Найдем площадь четырехугольника на рисунке.
Решение:
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным 5. Высоты этих треугольников равны 2 и 3. Тогда площадь четырёхугольника равна сумме площадей двух треугольников:
Ответ: 12,5.
В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Задача 17. Найдем площадь треугольника, изображенного на клетчатой бумаге.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной 5 и трёх прямоугольных треугольников. Видите их на рисунке? Получаем:
Ответ: 10,5.
Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.
Задача 18.
Найдите площадь сектора круга радиуса 1, длина дуги которого равна 2.
Решение:
На этом рисунке мы видим часть круга. Площадь всего круга равна так как
Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна
(так как R = 1), а длина дуги данного сектора равна 2, следовательно, длина дуги в
раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в
раз меньше, чем полный круг (то есть 360 градусов). Значит, и площадь сектора будет в
раз меньше, чем площадь всего круга.
Ответ: 1.
Формула Пика
Покажем, как вычислять площадь фигуры, изображенной на координатной плоскости, с помощью формулы Пика.
Задача 19. Найдите площадь многоугольника АВСDE, изображенного на рисунке.
Первый способ:
Площадь многоугольника ABCDE равна сумме площадей треугольника BCD, трапеции BKDE и треугольника AKE.
Имеем:
Второй способ – применить формулу Пика.
Назовем точку координатной плоскости целочисленной, если обе ее координаты — целые числа. На нашем рисунке это точки на пересечениях линий, разделяющих клетчатую бумагу на клетки.
Площадь многоугольника с целочисленными вершинами равна

Здесь В — количество целочисленных точек внутри многоугольника, Г — количество целочисленных точек на границе многоугольника.
Главное — аккуратно посчитать. На нашем рисунке
В = 24 (показаны зеленым),
Г = 8 (показаны красным),
S = 24 + — 1 = 27.
Ответ: 27.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Все формулы по геометрии. Площади фигур» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.05.2023
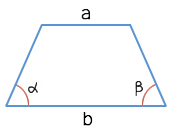
1. Формула площади равнобедренной трапеции через стороны и угол
а – нижнее основание
b – верхнее основание
с – равные боковые стороны
α – угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S ):
Формула площади равнобедренной трапеции через стороны и угол, (S ):
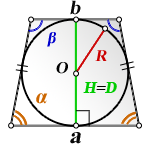
2. Формулы площади равнобедренной трапеции если в нее вписана окружность
R – радиус вписанной окружности
D – диаметр вписанной окружности
O – центр вписанной окружности
H – высота трапеции
α, β – углы трапеции
а – нижнее основание
b – верхнее основание
Формула площади равнобедренной трапеции через радиус вписанной окружности, (S ):
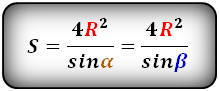
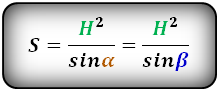
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:
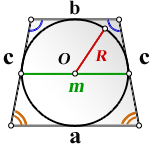
R – радиус вписанной окружности
m – средняя линия
O – центр вписанной окружности
c – боковые стороны
а – нижнее основание
b – верхнее основание
Формула площади равнобедренной трапеции через радиус вписанной окружности, стороны и среднюю линию (S ):
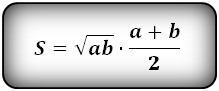
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
d – диагональ трапеции
α, β – углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S ):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
c – боковая сторона
m – средняя линия трапеции
α, β – углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):
5. Формула площади равнобедренной трапеции через основания и высоту
a – нижнее основание
b – верхнее основание
h – высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S ):
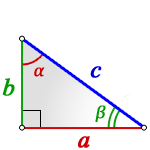
Прямоугольный треугольник, так же как и любой другой треугольник, имеет три стороны и три угла. Разница только в том, что один угол прямой, т. е. 90 градусов и два остальных, острых угла в сумме составляют, тоже 90 градусов.
Две стороны, которые формируют прямой угол, называют катетами, а третья сторона напротив прямого угла, называется – гипотенуза
1. Если известны только катеты
a, b – катеты треугольника
Формула площади треугольника через катеты ( S ) :
2. Если известны острый угол и гипотенуза или катет
c – гипотенуза
a, b – катеты
α, β – острые углы
Формулы площади прямоугольного треугольника через гипотенузу и угол ( S ) :
Формулы площади прямоугольного треугольника через катет и угол ( S ) :
Как известно, сумма острых углов в прямоугольном треугольнике равна 90 градусов, а если
то справедливы следующие тождества:
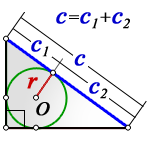
3. Если известны радиус вписанной окружности и гипотенуза
c – гипотенуза
c1, c2 – отрезки полученные делением гипотенузы, точкой касания окружности
r – радиус вписанной окружности
О – центр вписанной окружности
Формулы площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу ( S ) :