Формула нахождения площади квадрата
Квадрат — это фигура, которая является частным случаем прямоугольника, из-за чего можно заметить схожесть некоторых алгоритмов. Способ вычисления всегда зависит от исходных данных. Чтобы узнать площадь квадрата, необходимо знать специальные формулы, рассмотрим пять из них.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Если известна длина стороны
Умножаем ее на то же число или возводим в квадрат.
S = a × a = a2, где S — площадь, a — сторона.
Эту формулу проходят в 3 классе. Остальные формулы третьеклассникам знать пока не нужно, но они пригодятся ученикам 8 класса.
Если нам дана диагональ
Возводим ее в квадрат и делим на два.
S = d2 : 2, где d — диагональ.
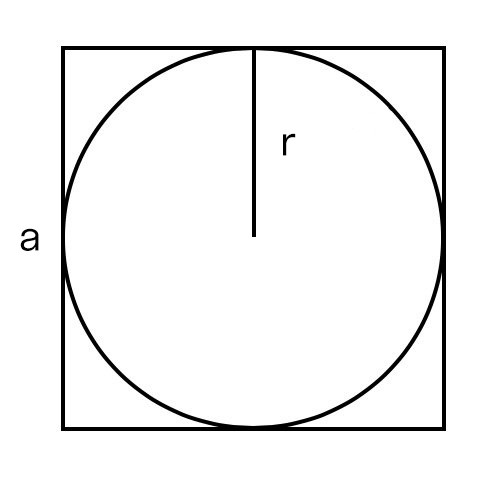
Если известен радиус вписанной окружности
Умножаем его квадрат на четыре.
S = 4 × r2, где r — это радиус вписанной окружности.
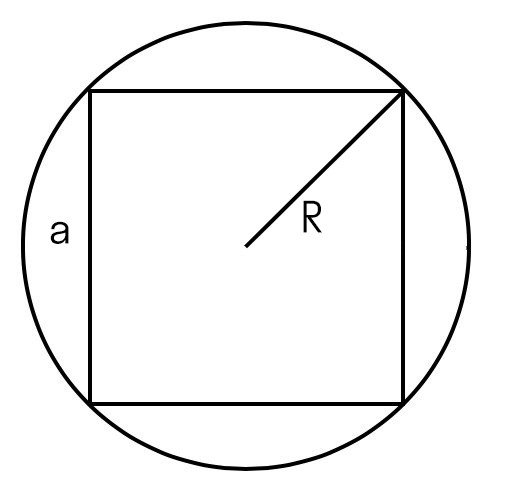
Если у нас есть радиус описанной окружности
Возведем его в квадрат и умножим на два.
S = 2 × R2, где R — это радиус описанной окружности.
Если есть периметр
Мы должны возвести его в квадрат и разделить на 16.
S = Р2 : 16, где Р — это периметр.
Периметр любого четырехугольника равен сумме длин всех его сторон.
Важно!
Задачку не решить, если длина и ширина даны в разных единицах. Для правильного решения переведите все данные к одной единице измерения, и все получится.
Популярные единицы измерения площади:
- квадратный миллиметр (мм2);
- квадратный сантиметр (см2);
- квадратный дециметр (дм2);
- квадратный метр (м2);
- квадратный километр (км2);
- гектар (га).
S квадрата. Решение задач
Мы разобрали пять формул для вычисления площади квадрата. А теперь давайте потренируемся!
Задание 1. Как найти площадь квадрата, диагональ которого равна 90 мм.
Как решаем:
-
Воспользуемся формулой: S = d2 : 2.
-
Подставим в формулу значение диагонали: S = 902 : 2 = 4050 мм2.
Ответ: 4050 мм2.
Задание 2. Окружность вписана в квадрат. Найдите площадь квадрата, если радиус окружности равен 24 см.
Как решаем:
-
Если окружность вписана в квадрат, то сторона квадрата равна диаметру:
a = d -
Диаметр окружности равен двум радиусам:
d = 2r -
Получается, что сторона равна двум радиусам:
a = 2r -
Используем формулу нахождения площади квадрата через сторону:
S = a2 -
Так как из пункта 3 мы получили, что сторона равна двум радиусам, то формула площади квадрата примет вид:
S = (2r)2
S = 4r2 -
Теперь подставим значение радиуса в формулу площади:
S = 4 × 242 = 2304 см2
Ответ: 2304 см2.
Площадь квадрата можно найти с помощью двух основных формул:
1) Через сторону.
2) Через диагональ.
Как найти площадь квадрата, если известна его сторона.
Как известно, квадрат – это частный случай прямоугольника, у которого все стороны равны.
Площадь прямоугольника равна произведению 2 его сторон:
Sпр = a * b, a и b – стороны прямоугольника.
В случае с квадратом a = b.
Таким образом, площадь квадрата будет находиться по формуле:
Sкв = a².
Например, если сторона квадрата равна 10 см., то его площадь = 10 * 10 = 100 см².
Как найти площадь квадрата, если известна его диагональ.
Диагональ делит квадрат на 2 прямоугольных треугольника. При этом диагональ является гипотенузой, а стороны квадрата – катетами.
Нам нужно выразить квадрат стороны через теорему Пифагора. Согласно данной теореме:
a*a + b*b = c*c.
a и b – катеты, c – гипотенуза.
В нашем случае a = b, а гипотенуза – это диагональ d.
Перепишем формулу в виде:
2a² = d².
a² = d² / 2.
Таким образом, если известна диагональ квадрата, то его площадь равна половине квадрата этой диагонали.
Например, если диагональ равна 10 см., то площадь квадрата = 10 * 10 / 2 = 50 см².

{S = a ^2}
На этой странице вы найдете удобный калькулятор для расчета площади квадрата и формулы, которые помогут найти площадь квадрата через его сторону, диагональ, периметр, а также радиусы вписанной и описанной окружности.
Квадрат – четырёхугольник, у которого все углы прямые (90 градусов) и все стороны равны между собой. Из-за своих свойств квадрат часто называют правильным четырехугольником.
Содержание:
- калькулятор площади квадрата
- формула площади квадрата через сторону
- формула площади квадрата через диагональ
- формула площади квадрата через радиус вписанной окружности
- формула площади квадрата через радиус описанной окружности
- формула площади квадрата через периметр
- примеры задач
Формула площади квадрата через сторону
S = a ^2
a – сторона квадрата
Формула площади квадрата через диагональ
S=dfrac{d^2}{2}
d – диагональ квадрата
Формула площади квадрата через радиус вписанной окружности
S = 4r^2
r – радиус вписанной окружности
Формула площади квадрата через радиус описанной окружности
S = 2R^2
R – радиус описанной окружности
Формула площади квадрата через периметр
S = dfrac{P^2}{16}
P – периметр квадрата
Примеры задач на нахождение площади квадрата
Задача 1
Найдите площадь квадрата если его диагональ равна 1.
Решение
Для решения задачи воспользуемся формулой.
S = dfrac{d^2}{2} = dfrac{1^2}{2} = dfrac{1}{2} = 0.5 : см^2
Ответ: 0.5 см²
Проверим ответ на калькуляторе .
Задача 2
Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Решение
Для решения этой задачи используем формулу площади квадрата через радиус описанной окружности.
S = 2R^2 = 2 cdot 83^2 = 2 cdot 6889 = 13778 : см^2
Ответ: 13778 см²
Проверим ответ с помощью калькулятора .
Задача 3
Найдите площадь квадрата если его сторона равна 8 см.
Решение
Используем первую формулу.
S = a ^2 = 8 ^2 = 64 : см^2
Ответ: 64 см²
Проверим результат на калькуляторе .
Задача 4
Найдите площадь квадрата периметр которого равен 456 см.
Решение
Используем формулу для площади квадрата через периметр.
S = dfrac{P^2}{16} = dfrac{456^2}{16} = dfrac{456 cdot cancel{456}^{ : 57}}{cancel{16}^{ : 2}} = dfrac{57 cdot cancel{456}^{ : 228}}{cancel{2}^{ : 1}} = 57 cdot 228 = 12996 : см^2
Ответ: 12996 см²
Проверка .
Задача 5
Найдите площадь квадрата со стороной 15 см.
Решение
Воспользуемся формулой площади квадрата через сторону.
S = a ^2 = 15 ^2 = 225 : см^2
Ответ: 225 см²
Проверка .
Что такое квадрат и понятие его площади
Квадрат — простейшая плоская геометрическая фигура. Является одновременно правильным четырёхугольником и прямоугольником, все стороны которого равны.
Состоит соответственно из четырёх равных сторон, четырёх вершин ABCD и прямых углов 90°.
Под площадью квадрата подразумевается пространство, ограниченное его сторонами (та часть плоскости, что внутри). Способов расчёта существует немного, а формулы для вычисления площади весьма простые.
Как найти площадь квадрата через сторону
Данный способ и калькулятор позволит найти площадь квадрата через значение длины его сторон — введите его в соответствующее поле. В зелёном поле автоматически выведется результат.
Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …
Как найти площадь квадрата через периметр
Данный способ и калькулятор позволит найти площадь квадрата через значение его периметра — введите его в соответствующее поле. В зелёном поле выведется результат.
Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …
Как найти площадь квадрата через диагональ
Данный способ и калькулятор позволит найти площадь квадрата через значение длины его диагонали — введите его в соответствующее поле. В зелёном поле получите результат.
Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …
Как найти площадь квадрата через радиус вписанной окружности
Данный способ и калькулятор позволит найти площадь квадрата через значение радиуса вписанной окружности — введите его в соответствующее поле. В зелёном поле выведется результат.
Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …
Как найти площадь квадрата через радиус описанной окружности
Данный способ и калькулятор позволит найти площадь квадрата через значение радиуса описанной окружности — введите его в соответствующее поле. В зелёном поле выведется результат автоматически.
Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …
Ваша оценка?
[Оценок: 5 / Средняя: 4.6]
Квадрат, свойства и формулы, площадь и периметр
Квадрат – это правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.
Квадрат (понятие, определение), диагональ квадрата
Свойства квадрата
Формулы квадрата. Площадь квадрата. Периметр квадрата
Видео
Площадь квадрата
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см
Площадь квадрата вычисляется таким же образом, как и площадь прямоугольника — длину умножают на ширину.
Вычислим площадь квадрата со стороной 3 см. Умножим длину 3 см на ширину 3 см
3 × 3 = 9
В данном случае требовалось узнать сколько квадратов со стороной 1 см содержится в исходном квадрате. В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:
Умножив длину на ширину, мы получили выражение 3 × 3, а это есть произведение двух одинаковых множителей, каждый из которых равен 3. Иными словами выражение 3 × 3 представляет собой вторую степень числа 3. А значит процесс вычисления площади квадрата можно записать в виде степени 32.
Поэтому вторую степень числа называют квадратом числа. При вычислении второй степени числа a, человек тем самым находит площадь квадрата со стороной a. Операцию возведения числа во вторую степень по другому называют возведением в квадрат.
Как найти площадь квадрата?
[ad3]
Вычисление площади данной фигуры можно просто и легко объяснить на примере:
- предположим, что сторона квадрата равна 8 метрам;
- для подсчета площади любого прямоугольника нужно умножить значение одной его стороны на другую (8 х 8 = 64);
- поскольку мы умножаем метры на метры, то в результате получаем квадратные метры (м2).
Площадь геометрической фигуры
Площадь геометрической фигуры — это число, которое характеризует размер данной фигуры.
Следует уточнить, что речь в данном случае идёт о площади на плоскости. Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.
Площадь измеряется в квадратных единицах. Под квадратными единицами подразумевают квадраты, стороны которых равны единице. Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.
Измерить площадь какой-нибудь фигуры означает выяснить сколько квадратных единиц содержится в данной фигуре.
Например, площадь следующего прямоугольника равна трём квадратным сантиметрам:
Это потому что в данном прямоугольнике содержится три квадрата, каждый из которых имеет сторону, равную одному сантиметру:
Справа представлен квадрат со стороной 1 см (он в данном случае является квадратной единицей). Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза.
Следующий прямоугольник имеет площадь, равную шести квадратным сантиметрам:
Это потому что в данном прямоугольнике содержится шесть квадратов, каждый из которых имеет сторону, равную одному сантиметру:
Допустим, потребовалось измерить площадь следующей комнаты:
Определимся в каких квадратах будем измерять площадь. В данном случае площадь удобно измерить в квадратных метрах:
Итак, наша задача состоит в том, чтобы определить сколько таких квадратов со стороной 1 м содержится в исходной комнате. Заполним этим квадратом всю комнату:
Видим, что квадратный метр содержится в комнате 12 раз. Значит, площадь комнаты составляет 12 квадратных метров.
Свойства квадрата:
1. Длины всех сторон равны.
Рис. 3. Квадрат
AB = BC = CD = AD
2. Противоположные стороны квадрата параллельны.
Рис. 4. Квадрат
AB||CD, BC||AD
3. Все углы квадрата прямые. Каждый из них равен 90°.
Рис. 5. Квадрат
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
4. Сумма углов квадрата равна 360 градусам.
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°.
5. Диагонали квадрата равны между собой.
Рис. 6. Квадрат
AC = BD
6. Диагонали квадрата взаимно перпендикулярны.
Рис. 7. Квадрат
AC ┴ BD
7. Диагонали квадрата точкой пересечения делятся пополам.
Рис. 8. Квадрат
BO = OD = AO = OC
8. Угол между диагональю и стороной квадрата равен 45 градусам.
Рис. 9. Квадрат
∠BCA = ∠ACD = ∠DAC = ∠CAB = 45°
9. Диагонали квадрата являются биссектрисами углов и делят углы пополам.
Рис. 10. Квадрат
∠ABD = ∠DBC = ∠BCA = ∠ACD = ∠CDB = ∠BDA = ∠DAC = ∠CAB = 45°
10. Каждая из диагоналей делит квадрат на два равных равнобедренных прямоугольных треугольника.
Обе диагонали делят квадрат на 4 равных равнобедренных прямоугольных треугольника.
Рис. 11. Квадрат
△ABD = △CBD = △ABC = △ACD,
△AOB = △BOC = △COD = △AOD
11. Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружности.
Рис. 12. Квадрат