Как найти площадь квадрата если знаешь диагональ - Сайт, где вы сможете решить свои вопросы

Загрузить PDF

Наиболее распространенной формулой для вычисления площади квадрата является следующая: S = a². Но иногда в задаче дана только диагональ квадрата, то есть отрезок, соединяющий противоположные вершины. Если вы знакомы с прямоугольными треугольниками, для вычисления площади квадрата можно воспользоваться формулой, которая включает диагональ.

1

Нарисуйте квадрат. У квадрата четыре равные стороны.^[1] Допустим, что длина каждой стороны равна а.
2

Посмотрите на основную формулу для вычисления площади квадрата. Площадь квадрата равна произведению длины на ширину. Так как каждая сторона квадрата равна а, формула для вычисления площади квадрата: S = а х а = а². Эта формула понадобится далее.
3

Соедините два противоположных угла квадрата, чтобы провести диагональ. Допустим, что длина диагонали равна d. Диагональ делит квадрат на два прямоугольных треугольника.
4
К одному из треугольников примените теорему Пифагора. По теореме Пифагора^[2] можно найти гипотенузу (самую длинную сторону) прямоугольного треугольника: $a^{2}+b^{2}=c^{2}$ , где а и b — катеты, с — гипотенуза. Разделив квадрат на два прямоугольных треугольника, примените эту формулу к одному из них.
- Катетами прямоугольного треугольника являются стороны квадрата, каждая из которых равна а.
- Гипотенузой является диагональ квадрата, равная d.
- $a^{2}+a^{2}=d^{2}$
5
6

Воспользуйтесь этой формулой для решения задачи. Полученную формулу S = ${frac {d^{2}}{2}}$ можно применять к любым квадратам: просто подставьте в нее значение диагонали (вместо d).

Реклама

1

Найдите диагональ по стороне.^[3] Если сторона квадрата равна а, а диагональ равна d, теорема Пифагора запишется так: $2a^{2}=d^{2}$ . По этой формуле можно вычислить диагональ, если сторона квадрата известна.
2
3
Проверьте правильность формулы. Верность математического вывода формулы S = ${frac {d^{2}}{2}}$ не вызывает сомнений, но можно ли проверить правильность формулы наглядно? Допустим, что сторона второго квадрата равна d, то есть диагонали первого квадрата; тогда площадь второго квадрата равна $d^{2}$ . Так как формула для вычисления площади S = ${frac {d^{2}}{2}}$ , можно заключить, что площадь второго квадрата в два раза больше площади первого квадрата. Проверьте это наглядно:
- На бумаге нарисуйте первый квадрат. Убедитесь, что все стороны равны.
- Измерьте диагональ. Нарисуйте второй квадрат: каждая его сторона должна быть равна диагонали первого квадрата.
- Нарисуйте копию первого квадрата, а затем вырежьте три квадрата.
- Разрежьте два меньших квадрата так, чтобы они поместились в большем квадрате. Два меньших квадрата должны полностью покрыть больший квадрат, что доказывает, что площадь большего квадрата в два раза больше площади меньшего квадрата.
Реклама

Советы

Если калькулятора нет, но необходимо получить точное значение √2, извлеките корень вручную. Например, примените метод Ньютона-Рафсона.^[4]
Приведенная формула используется во многих областях, в том числе в кристаллографии, химии и технике. Например, при помощи этой формулы можно вычислить площадь ландшафта, который виден воочию или на фотографии/рисунке. Для этого измерьте пройденный путь, а затем проведите воображаемую диагональ.
Если вы предпочитаете изучать математику с наглядными примерами или хотите узнать, как использовать диаграммы и графики в искусстве, читайте статьи на сайте wikiHow (например, в категориях «Математика», «Графические программы», «Офисные программы» и других).

Об этой статье

Эту страницу просматривали 50 242 раза.

Была ли эта статья полезной?

Источник

Площадь квадрата можно найти с помощью двух основных формул:

1) Через сторону.

2) Через диагональ.

Как найти площадь квадрата, если известна его сторона.

Как известно, квадрат – это частный случай прямоугольника, у которого все стороны равны.

Площадь прямоугольника равна произведению 2 его сторон:

Sпр = a * b, a и b – стороны прямоугольника.

В случае с квадратом a = b.

Таким образом, площадь квадрата будет находиться по формуле:

Sкв = a².

Например, если сторона квадрата равна 10 см., то его площадь = 10 * 10 = 100 см².

Как найти площадь квадрата, если известна его диагональ.

Диагональ делит квадрат на 2 прямоугольных треугольника. При этом диагональ является гипотенузой, а стороны квадрата – катетами.

Нам нужно выразить квадрат стороны через теорему Пифагора. Согласно данной теореме:

a*a + b*b = c*c.

a и b – катеты, c – гипотенуза.

В нашем случае a = b, а гипотенуза – это диагональ d.

Перепишем формулу в виде:

2a² = d².

a² = d² / 2.

Таким образом, если известна диагональ квадрата, то его площадь равна половине квадрата этой диагонали.

Например, если диагональ равна 10 см., то площадь квадрата = 10 * 10 / 2 = 50 см².

Источник

Лучший ответ

werer salak

Знаток

(295)

12 лет назад

допустим диагональ равен 8 см
по теореме пифагора
x2+x2=8*8
2*x2=64
x2 – площадь квадрата
x2=64/2=32
Ответ: 32

Остальные ответы

shadow

Оракул

(51433)

12 лет назад

по теореме Пифагора

GepardMove

Мастер

(1352)

12 лет назад

диагональ в квадрате подели на 2. Вот тебе и площадь квадрата

neADekvatnoe chydo 8)

Профи

(641)

12 лет назад

пусть квадрат АВСД, ВД- диагональ, тогда АВ^2+АД^2= ВД^2, но стороны у нас равны, значит 2АВ^2=ВД^2, АВ= ВД/ корень из 2 – это найдёшь сторону, а площадь уж найдёшь)))

Источник: Я

Диана Абрикосова

Мыслитель

(6021)

12 лет назад

Если обозначить диагональ а, тогда половина диагонали будет a /.2
Составим уравнение, используя теорему Пифагора.
(а /2) 2 + (a /2)2 = a2 /2 То есть, а в квадрате деленное на 2
Тогда сторона квадрата будет а корень из 2, деленное на 2

Источник

{S = a ^2}

На этой странице вы найдете удобный калькулятор для расчета площади квадрата и формулы, которые помогут найти площадь квадрата через его сторону, диагональ, периметр, а также радиусы вписанной и описанной окружности.

Квадрат – четырёхугольник, у которого все углы прямые (90 градусов) и все стороны равны между собой. Из-за своих свойств квадрат часто называют правильным четырехугольником.

Содержание:

калькулятор площади квадрата
формула площади квадрата через сторону
формула площади квадрата через диагональ
формула площади квадрата через радиус вписанной окружности
формула площади квадрата через радиус описанной окружности
формула площади квадрата через периметр
примеры задач

Формула площади квадрата через сторону

S = a ^2

a – сторона квадрата

Формула площади квадрата через диагональ

S=dfrac{d^2}{2}

d – диагональ квадрата

Формула площади квадрата через радиус вписанной окружности

S = 4r^2

r – радиус вписанной окружности

Формула площади квадрата через радиус описанной окружности

S = 2R^2

R – радиус описанной окружности

Формула площади квадрата через периметр

S = dfrac{P^2}{16}

P – периметр квадрата

Примеры задач на нахождение площади квадрата

Задача 1

Найдите площадь квадрата если его диагональ равна 1.

Решение

Для решения задачи воспользуемся формулой.

S = dfrac{d^2}{2} = dfrac{1^2}{2} = dfrac{1}{2} = 0.5 : см^2

Ответ: 0.5 см²

Проверим ответ на калькуляторе .

Задача 2

Найдите площадь квадрата, описанного вокруг окружности радиуса 83.

Решение

Для решения этой задачи используем формулу площади квадрата через радиус описанной окружности.

S = 2R^2 = 2 cdot 83^2 = 2 cdot 6889 = 13778 : см^2

Ответ: 13778 см²

Проверим ответ с помощью калькулятора .

Задача 3

Найдите площадь квадрата если его сторона равна 8 см.

Решение

Используем первую формулу.

S = a ^2 = 8 ^2 = 64 : см^2

Ответ: 64 см²

Проверим результат на калькуляторе .

Задача 4

Найдите площадь квадрата периметр которого равен 456 см.

Решение

Используем формулу для площади квадрата через периметр.

S = dfrac{P^2}{16} = dfrac{456^2}{16} = dfrac{456 cdot cancel{456}^{ : 57}}{cancel{16}^{ : 2}} = dfrac{57 cdot cancel{456}^{ : 228}}{cancel{2}^{ : 1}} = 57 cdot 228 = 12996 : см^2

Ответ: 12996 см²

Проверка .

Задача 5

Найдите площадь квадрата со стороной 15 см.

Решение

Воспользуемся формулой площади квадрата через сторону.

S = a ^2 = 15 ^2 = 225 : см^2

Ответ: 225 см²

Проверка .

Источник

Как рассчитать площадь квадрата

На данной странице калькулятор поможет рассчитать площадь квадрата онлайн. Для расчета задайте длину стороны или диагональ.

Квадрат — это правильный четырёхугольник. У него все стороны и углы равны между собой. Квадрат есть частный вид прямоугольника, а также частный вид ромба.

Через сторону

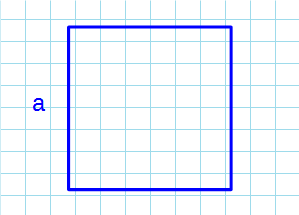
Формула для нахождения площади квадрата через сторону:

a – сторона квадрата.

Через диагональ

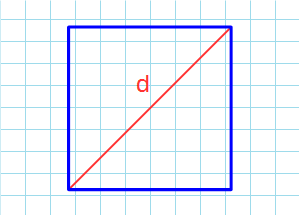
Формула для нахождения площади квадрата через диагональ:

d – диагональ квадрата.

Источник

Советы

Об этой статье

Была ли эта статья полезной?

Содержание:

Формула площади квадрата через сторону

Формула площади квадрата через диагональ

Формула площади квадрата через радиус вписанной окружности

Формула площади квадрата через радиус описанной окружности

Формула площади квадрата через периметр

Примеры задач на нахождение площади квадрата

Как рассчитать площадь квадрата

Через сторону

Через диагональ

Вам также может понравиться

Как в питере найти мужчину для

Как найти хороших квартирантов заговор

Как можно найти макбук

Добавить комментарий Отменить ответ